↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Training large diffusion models from scratch is computationally expensive. Existing fine-tuning methods often overlook the fundamental transfer characteristics of these models, leading to suboptimal performance. The challenge lies in effectively transferring knowledge from a pre-trained model to a specific downstream task without causing catastrophic forgetting or overfitting.
This paper proposes Diff-Tuning, a novel method that addresses these limitations. Diff-Tuning leverages the observed ‘chain of forgetting’—a trend where the transferability of a pre-trained model decreases monotonically along the reverse denoising process. By integrating two objectives—knowledge retention and knowledge reconsolidation—Diff-Tuning strategically balances the retention of general knowledge and the adaptation of task-specific information, resulting in significant performance improvements over standard fine-tuning in both conditional and controllable generation tasks.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the high computational cost of fine-tuning large diffusion models by introducing a novel transfer learning method. This method, Diff-Tuning, is general and efficient, improving performance over standard fine-tuning across multiple tasks. It also opens new avenues for research in parameter-efficient transfer learning, making it valuable for researchers working with large-scale generative models.
Visual Insights#

This figure presents a case study that investigates the impact of using a pre-trained diffusion model instead of a fine-tuned model at various denoising steps during the reverse diffusion process. The left panel shows example images generated by directly replacing the fine-tuned denoiser with the original pre-trained denoiser at different stages, illustrating how the fine-tuned model’s performance relative to the pre-trained model changes as we incrementally replace more steps. The right panel shows a plot demonstrating how the Fréchet Inception Distance (FID), a metric used for evaluating generative model performance, changes when replacing different percentages of the fine-tuned model with the pre-trained model. This plot illustrates that performance improves at the end of the diffusion process but decreases as we move towards the beginning, indicating the presence of a “chain of forgetting” phenomenon.
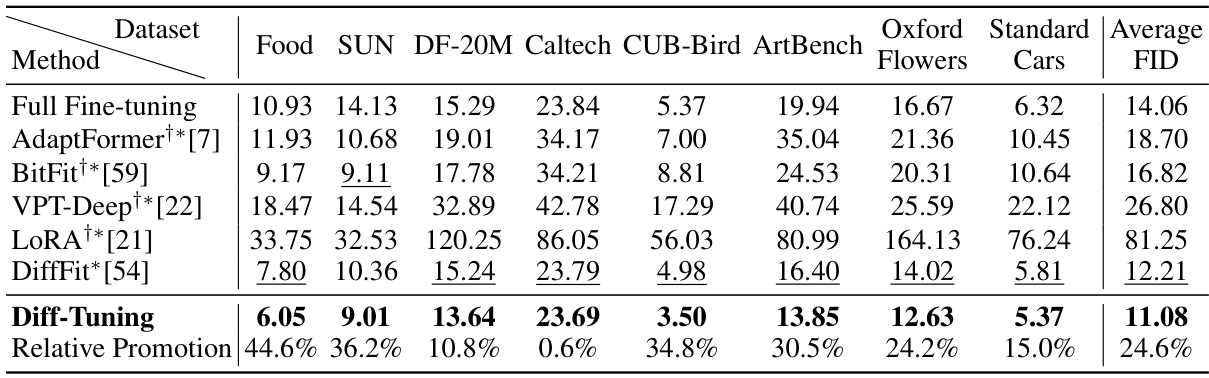
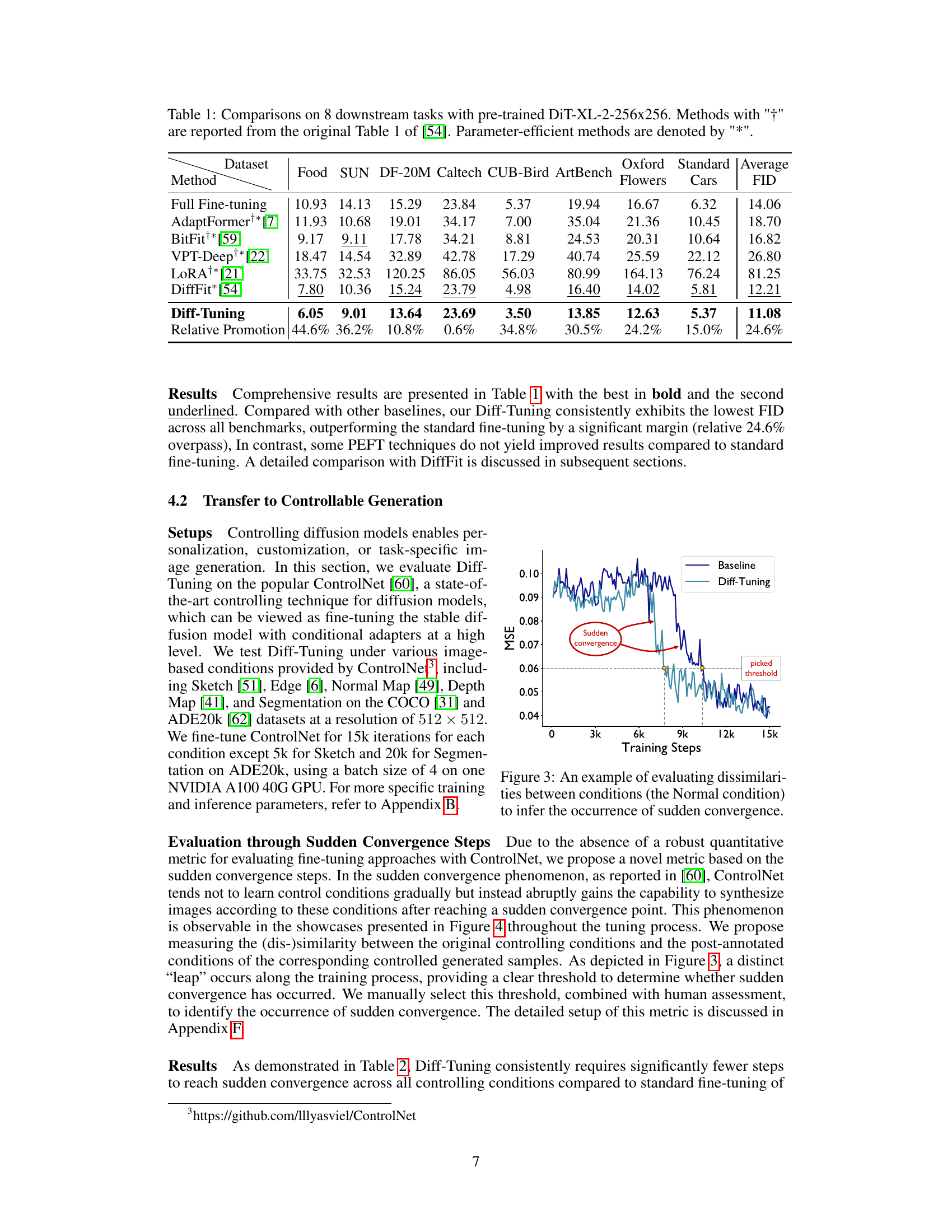
This table presents a comparison of different methods for fine-tuning a pre-trained Diffusion Transformer model (DiT-XL-2-256x256) on eight downstream tasks. The methods compared include full fine-tuning and several parameter-efficient fine-tuning (PEFT) techniques. The table shows the Fréchet Inception Distance (FID) score for each method on each dataset, a lower FID indicating better performance. The ‘Relative Promotion’ row indicates the percentage improvement of Diff-Tuning over standard fine-tuning for each dataset and on average.
In-depth insights#
Diff-Tuning: Overview#
Diff-Tuning presents a novel approach to transfer learning for diffusion models, addressing the limitations of standard fine-tuning. It leverages the observed “chain of forgetting,” a phenomenon where the transferability of a pre-trained model diminishes monotonically as one progresses through the reverse denoising process. Diff-Tuning strategically balances knowledge retention and reconsolidation. It prioritizes retaining general denoising skills from the pre-trained model while adapting high-level, domain-specific shaping characteristics to the target task. This is achieved through a dual-objective training strategy that encourages knowledge retention at the beginning of the denoising chain and knowledge adaptation toward the end. This approach offers a simple yet effective method for enhancing transferability and potentially improves training speed and reduces overfitting. The method’s generality is demonstrated through successful application in both conditional and controllable generation tasks, highlighting its potential impact on various downstream applications of diffusion models.
Chain of Forgetting#
The concept of “Chain of Forgetting” in the context of diffusion models presents a novel perspective on the transferability of pre-trained models. It posits that as fine-tuning progresses through the reverse denoising process, the model gradually loses its ability to retain high-level, domain-specific knowledge while preserving low-level features. This monotonic forgetting trend is attributed to the inherent characteristics of diffusion models, where initial stages focus on high-level object representation and later stages refine details. The significance lies in the implication that a naive parameter-efficient fine-tuning approach might lead to suboptimal results by overfitting or neglecting the transfer properties of these different stages. Diff-Tuning, a proposed method, directly addresses this by specifically targeting knowledge retention and reconsolidation, thus seeking to balance the inevitable forgetting with the desirable adaptation to downstream tasks. This framing suggests that careful consideration of the specific characteristics of different stages is crucial for effective transfer learning in diffusion models, potentially outperforming existing methods that treat all parameters uniformly.
Transfer Learning#
Transfer learning, a core concept in machine learning, is thoroughly examined in the context of diffusion models. The paper highlights the limitations of directly applying standard fine-tuning techniques due to issues like overfitting and catastrophic forgetting. It introduces the novel concept of a ‘chain of forgetting,’ where higher-level features are less transferable than lower-level ones during the reverse diffusion process. This observation motivates the development of novel transfer learning methods such as Diff-Tuning. Diff-Tuning leverages this chain of forgetting to develop a more effective approach, combining knowledge retention with knowledge reconsolidation. The paper emphasizes that parameter-efficient transfer learning techniques can also benefit from Diff-Tuning. The core idea is to preserve low-level denoising capabilities while adapting higher-level features to the target task, offering a more nuanced and effective strategy for transferring knowledge in diffusion models.
Experimental Results#
A robust ‘Experimental Results’ section should present findings in a clear, structured manner. It should begin with a concise overview of the experimental setup, including datasets used, metrics employed, and comparison baselines. Detailed tables and figures are crucial, illustrating key performance indicators and statistical significance (p-values or confidence intervals). Visualizations should be intuitive and clearly labeled to easily understand trends. The discussion should move beyond simply stating results; it must analyze the results in the context of the research hypothesis, highlighting achievements, limitations, and unexpected findings. Comparison to baselines must be thorough and should include appropriate statistical tests to validate claims of improvement. The section should also discuss potential sources of error and their impact on the results’s reliability. Finally, it’s important to relate the findings back to the broader context of the study’s aims, demonstrating how the experimental results contribute to a more comprehensive understanding of the research problem.
Future Directions#
Future research could explore several promising avenues. Extending Diff-Tuning’s applicability to diverse diffusion model architectures beyond the tested DiT and Stable Diffusion models would broaden its impact. Investigating optimal strategies for selecting the retention and reconsolidation coefficients, perhaps through data-driven methods or adaptive scheduling, could further enhance performance. A more thorough investigation into the interplay between Diff-Tuning and existing parameter-efficient fine-tuning techniques is warranted, potentially revealing synergistic combinations. Finally, exploring Diff-Tuning’s effectiveness in truly continual learning scenarios with non-stationary data streams, and assessing its robustness to catastrophic forgetting, would validate its potential in dynamic real-world applications.
More visual insights#
More on figures
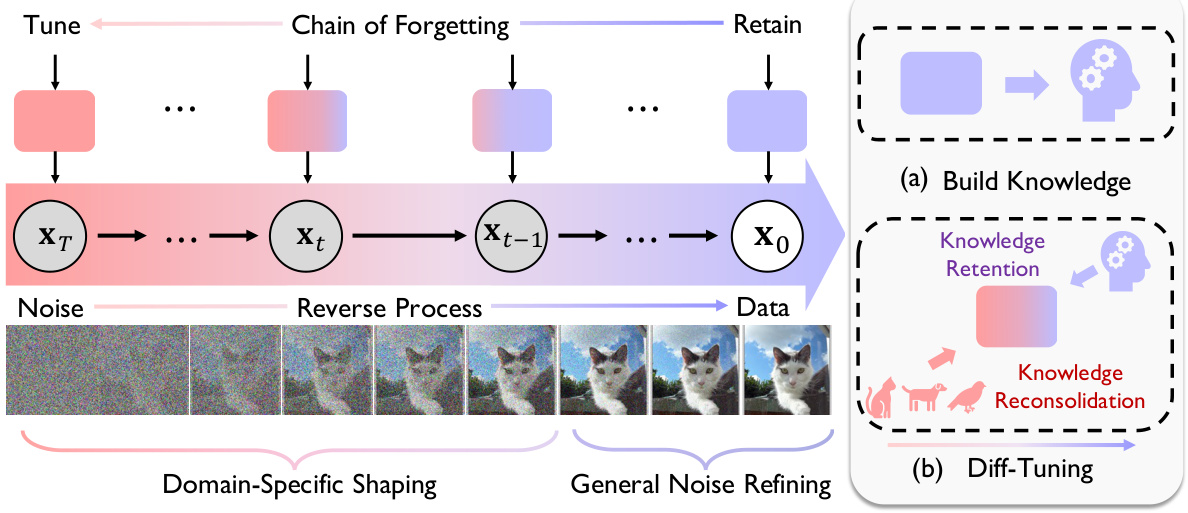
This figure illustrates the concept of ‘chain of forgetting’ in diffusion models. The left side shows a diffusion model’s reverse process, where noise is progressively removed to generate an image. As the process moves from high-level noise to low-level noise (from left to right), the model’s ability to generalize to new domains decreases (forgetting trend). The right side presents Diff-Tuning’s strategy. First, knowledge from a pre-trained model is preserved in a ‘knowledge bank’ (a). Then, Diff-Tuning integrates ‘knowledge retention’ (preserving the general denoising capabilities of the pre-trained model) and ‘knowledge reconsolidation’ (adapting the model to downstream task-specific domains) during fine-tuning (b), effectively balancing forgetting and retention by utilizing the chain of forgetting trend.
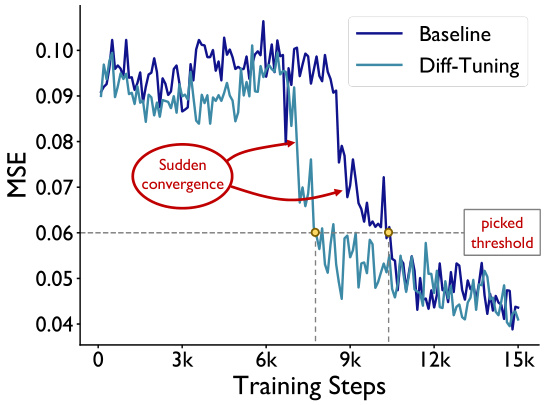
The figure shows a case study evaluating the dissimilarities between conditions to infer the occurrence of sudden convergence in ControlNet fine-tuning. The x-axis represents the training steps, and the y-axis represents the Mean Squared Error (MSE). Two lines are plotted: one for the baseline ControlNet fine-tuning and one for the Diff-Tuning method. The Diff-Tuning line shows a steeper drop in MSE, indicating faster convergence. A horizontal dashed line marks a picked threshold to define the sudden convergence. The points where the lines cross the threshold are marked with yellow circles. The red oval highlights the ‘sudden convergence’ region where the MSE drops significantly.

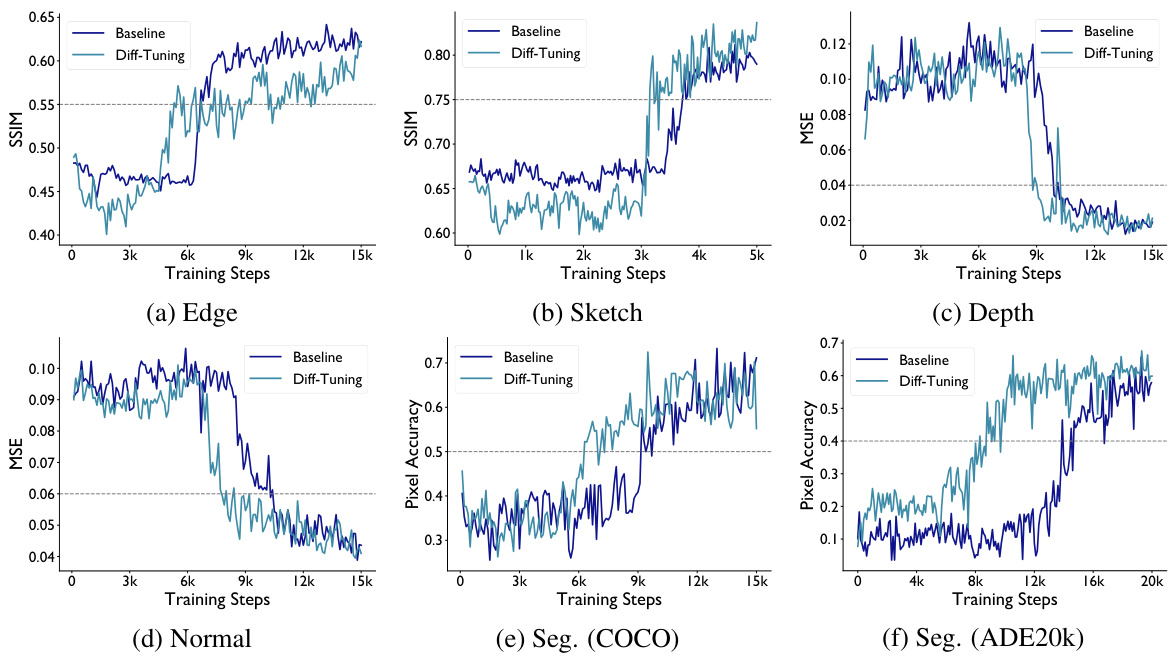
This figure shows a qualitative comparison of Diff-Tuning and standard ControlNet on five different control conditions: Edge, Sketch, Depth, Normal, and Segmentation. For each condition, sample images generated at various training steps are displayed. Red boxes highlight the point at which ‘sudden convergence’ occurs—the point where the model rapidly acquires the ability to generate images that accurately reflect the control condition. The figure demonstrates that Diff-Tuning consistently reaches sudden convergence significantly faster than standard ControlNet, suggesting a more efficient transfer learning process.
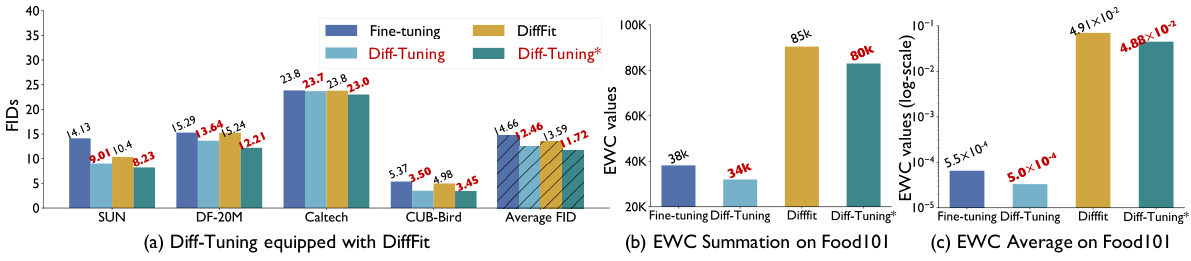
This figure shows three subfigures that analyze the performance of Diff-Tuning in comparison to standard fine-tuning and DiffFit. Subfigure (a) shows the FID (Fréchet Inception Distance) scores for several downstream datasets for each method, demonstrating the superior performance of Diff-Tuning. Subfigures (b) and (c) present the EWC (Elastic Weight Consolidation) values, a measure of catastrophic forgetting. The total EWC and average EWC across all tunable parameters are shown for the different methods. These subfigures show that Diff-Tuning achieves lower EWC values compared to the other methods, indicating less catastrophic forgetting.

This figure presents four subplots, each showing a different analysis related to the Diff-Tuning method. (a) Convergence analysis on SUN397 dataset shows the FID scores over training steps for various methods, highlighting Diff-Tuning’s faster convergence. (b) Ablation study on DF20M dataset demonstrates the impact of individual components (retention and reconsolidation) of Diff-Tuning, showing their complementary roles. (c) Sensitivity analysis on the Stanford Cars dataset explores the influence of the reconsolidation coefficient function ψ(t), which relates to the chain of forgetting. (d) Analysis of the number of samples in memory shows the relationship between the number of samples in the augmented dataset and the performance, indicating a point of diminishing returns.
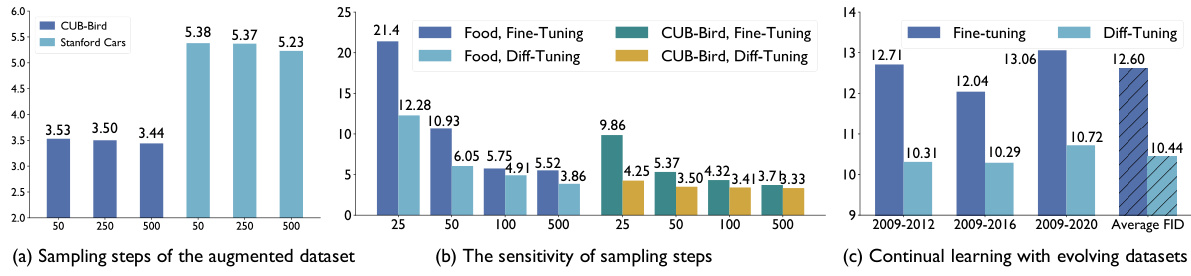
This figure shows three subfigures demonstrating different aspects of Diff-Tuning. Subfigure (a) illustrates the effect of the size of the augmented dataset on the model’s performance for CUB-Bird and Stanford Cars datasets. It shows that increasing the size of the augmented dataset improves performance, but there are diminishing returns. Subfigure (b) demonstrates the influence of the number of sampling steps used in generating the augmented dataset. It shows that increasing the number of sampling steps also improves performance, but again there are diminishing returns. Subfigure (c) shows the results of using Diff-Tuning in a continual learning setup using the Evolving Image Search dataset. It shows that the model’s performance is consistently better when using Diff-Tuning than when using standard fine-tuning across multiple time periods.

This figure displays sample images from eight different datasets used in the paper for class-conditional image generation experiments. Each dataset represents a unique set of visual categories: Food101 (food items), SUN397 (scenes), DF20M (fungi), Caltech101 (objects), CUB-200-2011 (birds), ArtBench10 (artwork styles), Oxford Flowers (flowers), and Stanford Cars (cars). The images illustrate the variety and complexity of visual data used to evaluate the proposed method.
This figure shows two plots. The left plot is a case study of directly replacing the denoiser with the original pre-trained model on lightly disturbed data. It demonstrates the concept that a pre-trained model acts as a universal denoiser for lightly corrupted data, capable of recognizing and refining subtle distortions. The right plot shows the change in Fréchet Inception Distance (FID) as the denoising steps are incrementally replaced by the original pre-trained model, demonstrating the concept of ‘chain of forgetting’.
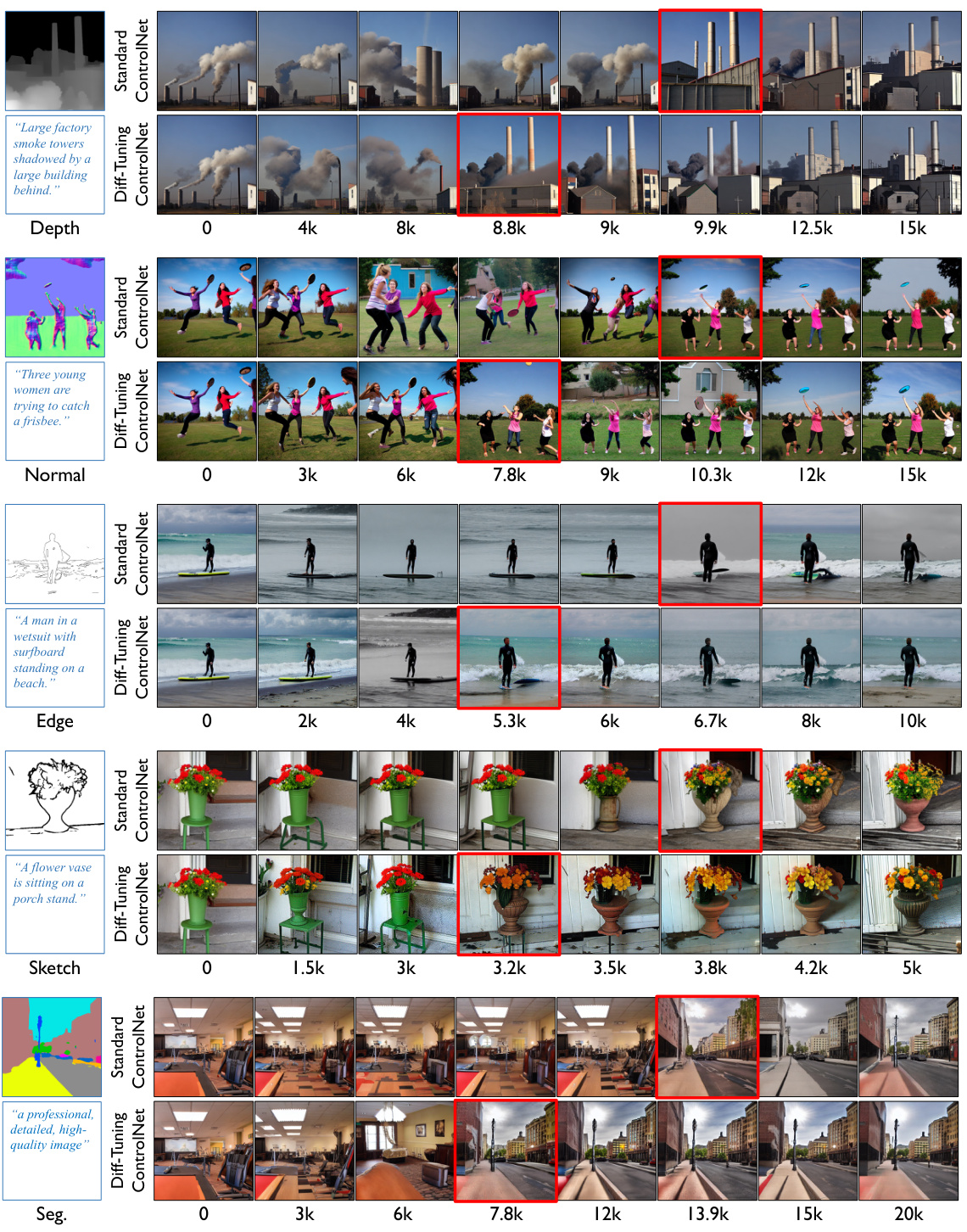
This figure shows a qualitative comparison of the results obtained using Diff-Tuning and standard ControlNet on five different control conditions. For each condition (Edge, Sketch, Depth, Normal, Segmentation), it displays image samples generated at various training steps. The red boxes highlight the training steps where ‘sudden convergence’ is observed; that is, where the model abruptly starts generating high-quality images corresponding to the control condition. The comparison visually demonstrates that Diff-Tuning achieves ‘sudden convergence’ much faster than the standard ControlNet, indicating that Diff-Tuning enhances the speed and quality of controllable generation in diffusion models.

This figure compares image generation results using standard ControlNet and Diff-Tuning ControlNet with edge control. Diff-Tuning produces images with better quality and more detail, despite having a lower Structural Similarity Index (SSIM) score than the standard ControlNet. This demonstrates that the SSIM metric does not fully capture the nuanced aspects of image quality and the importance of incorporating human assessment in evaluating generation quality.
More on tables

This table presents the results of an experiment comparing the number of steps to reach sudden convergence for standard ControlNet fine-tuning and ControlNet fine-tuning with Diff-Tuning applied. Five different control conditions (Sketch, Normal, Depth, Edge, and Segmentation) were tested using the Stable Diffusion model. The table shows the average number of steps needed for sudden convergence across all conditions and the percentage improvement achieved by using Diff-Tuning.

This table presents a comparison of different methods for fine-tuning a pre-trained Diffusion Transformer (DiT) model on eight downstream tasks. The table shows the Fréchet Inception Distance (FID) scores achieved by each method. The methods compared include full fine-tuning, several parameter-efficient fine-tuning (PEFT) methods, and the proposed Diff-Tuning method. Lower FID scores indicate better performance. The table highlights the improvement achieved by Diff-Tuning compared to other methods, particularly standard fine-tuning.
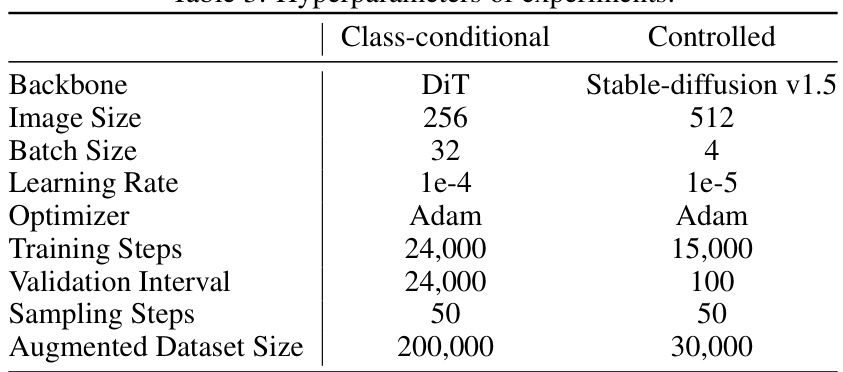
This table lists the hyperparameters used in the experiments described in the paper. It shows hyperparameters used for both class-conditional generation and controlled generation experiments, specifying different settings for the backbone model, image size, batch size, learning rate, optimizer, number of training steps, validation interval, number of sampling steps and the augmented dataset size used in Diff-Tuning.
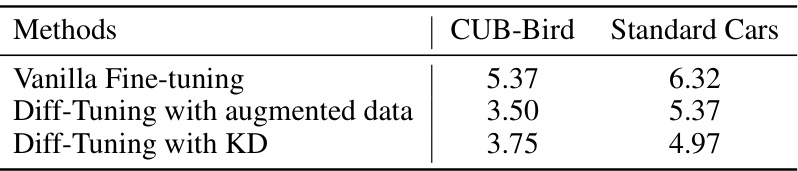
This table compares the Fréchet Inception Distance (FID) scores achieved by three different methods on the CUB-Bird and Standard Cars datasets. The methods are: Vanilla Fine-tuning (standard fine-tuning), Diff-Tuning with augmented data (using an augmented dataset for knowledge retention), and Diff-Tuning with KD (using knowledge distillation for knowledge retention). The table shows that Diff-Tuning, in both its augmented data and KD variants, significantly outperforms standard fine-tuning in terms of FID scores, demonstrating its effectiveness in improving the transferability of pre-trained diffusion models.
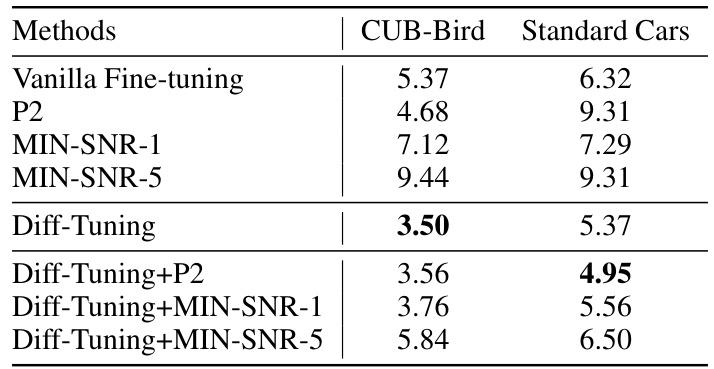
This table presents a comparison of different fine-tuning methods on eight downstream tasks using a pre-trained DiT-XL-2-256x256 model. It shows the Fréchet Inception Distance (FID) scores achieved by various methods, including full fine-tuning and several parameter-efficient fine-tuning (PEFT) techniques. The results highlight the performance of the proposed Diff-Tuning method compared to existing state-of-the-art approaches.

This table presents the results of fine-tuning the Energy-based Diffusion Model (EDM) on the CIFAR-10 dataset after pre-training on the ImageNet dataset. It compares the Fréchet Inception Distance (FID) score achieved using standard fine-tuning (‘Vanilla’) against the FID score obtained using the proposed Diff-Tuning method. The lower FID score indicates better performance in image generation.

This table presents the number of steps required to reach ‘sudden convergence’ for ControlNet and ControlNet enhanced with Diff-Tuning across five different control conditions (Sketch, Normal, Depth, Edge, and Segmentation on COCO/ADE20k datasets). Sudden convergence refers to the point where ControlNet abruptly gains the ability to synthesize images according to the specified control conditions, rather than learning gradually. The table highlights the significant improvement in convergence speed achieved by Diff-Tuning compared to the standard ControlNet.
Full paper#