General bounds on the quality of Bayesian coresets

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper significantly advances scalable Bayesian inference by providing general theoretical guarantees for Bayesian coresets, addressing limitations of existing methods and guiding future research in large-scale Bayesian modeling. It offers a more flexible and widely applicable framework for approximating posterior distributions, impacting various fields that leverage Bayesian methods for large datasets.

Visual Insights

#

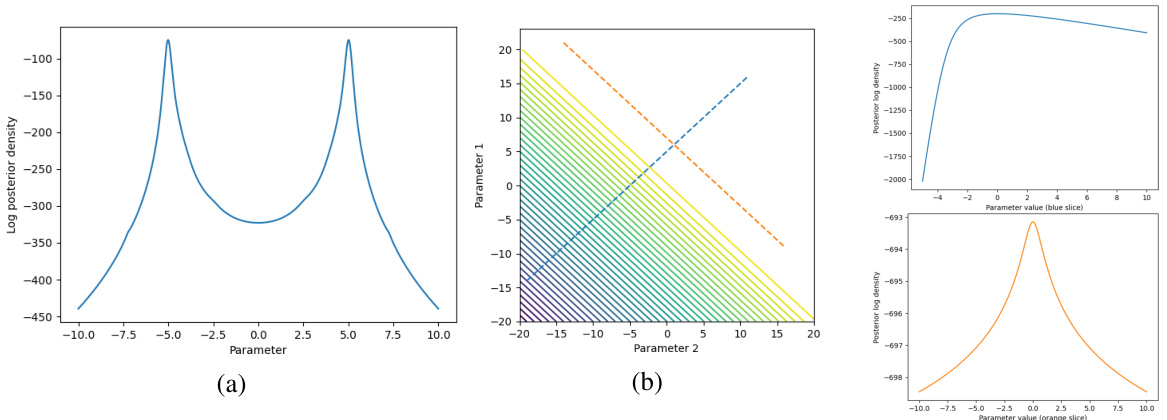
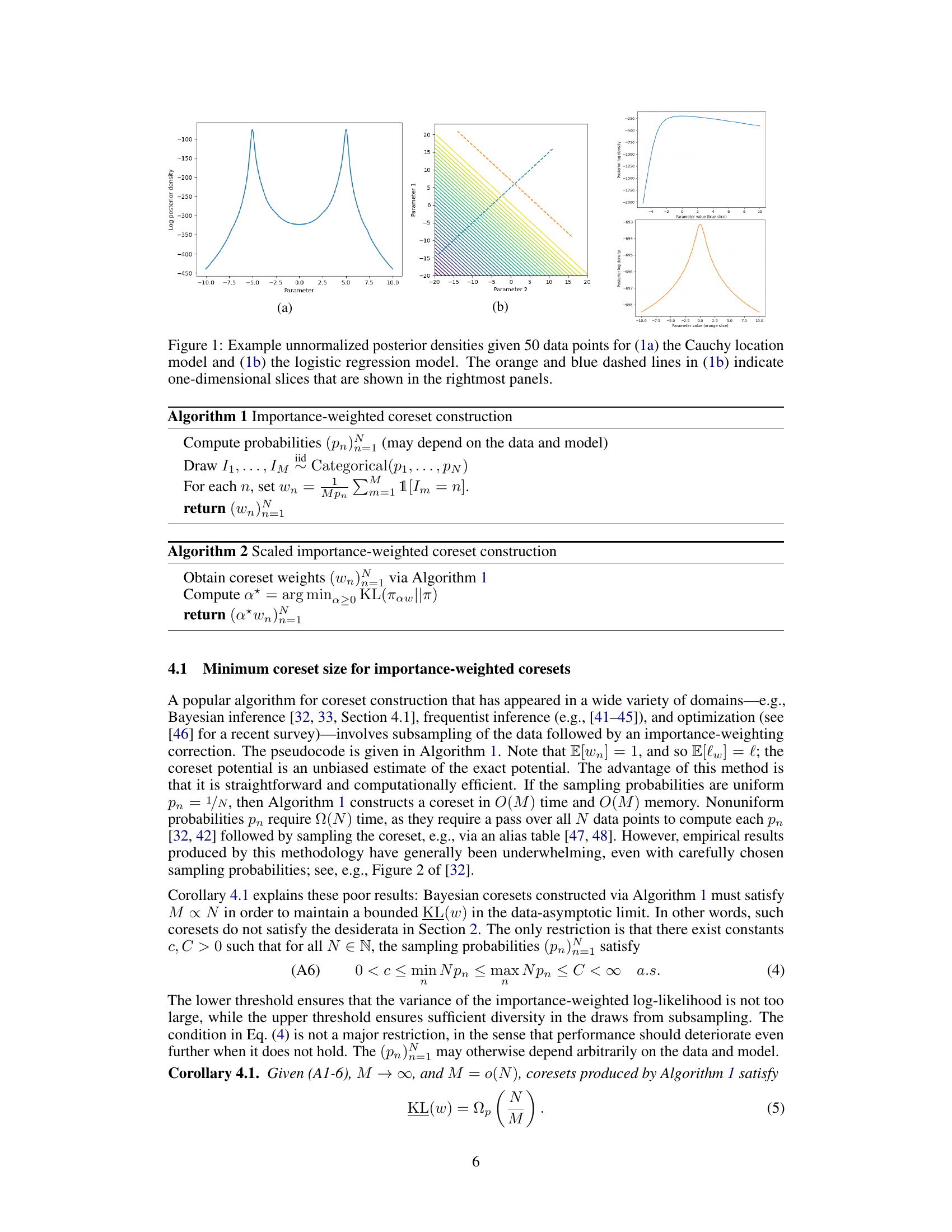
This figure shows the unnormalized posterior density for two different Bayesian models given 50 data points. Panel (a) displays a unimodal, symmetric posterior density for a Cauchy location model. Panel (b) shows a multimodal, asymmetric posterior density for a logistic regression model, with one-dimensional slices highlighted in orange and blue, that are further visualized in the rightmost panels of the figure. These example posteriors are used to illustrate the variety of model types considered in the paper.

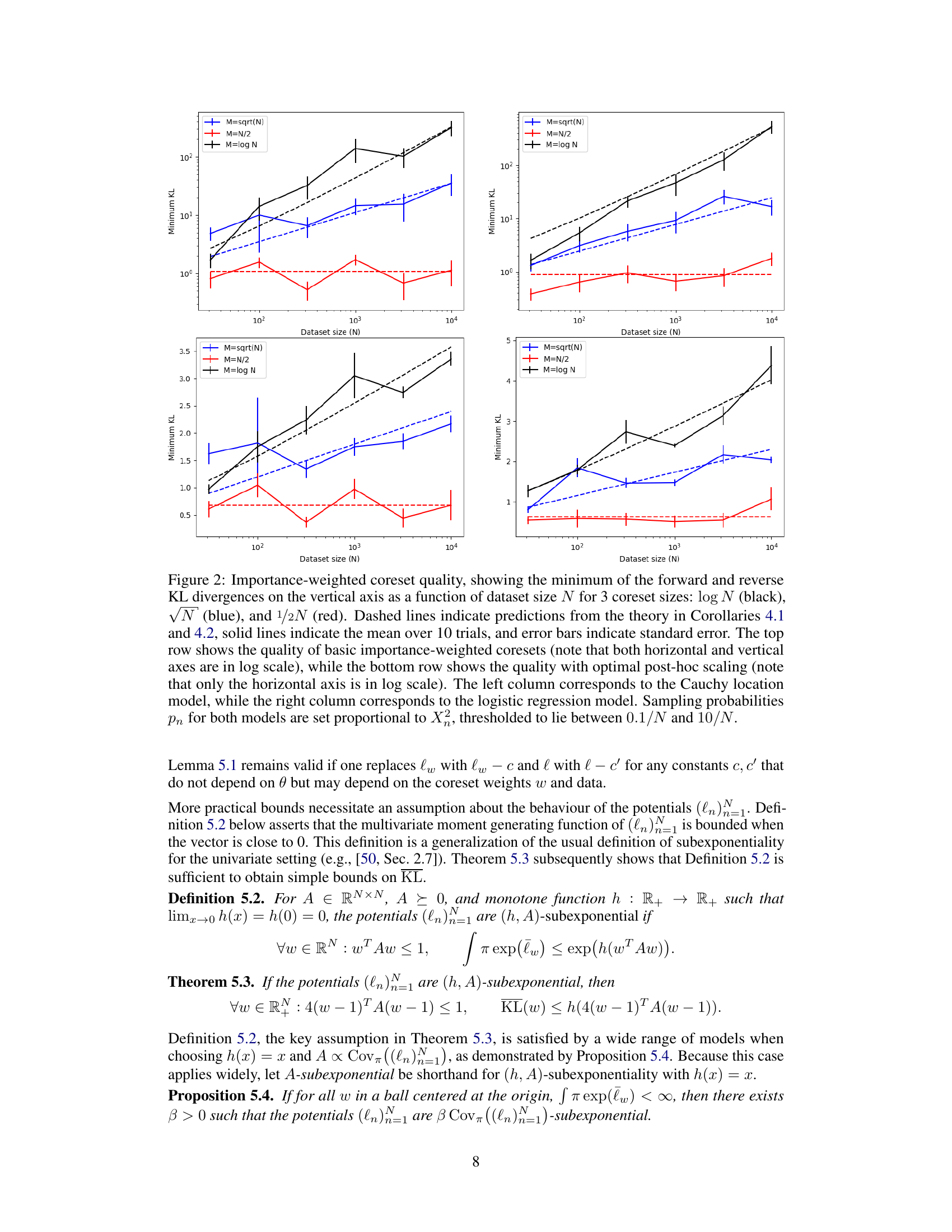
This figure empirically validates Corollaries 4.1 and 4.2, which concern the minimum coreset size for importance-weighted coresets. The plots show the minimum KL divergence between the true posterior and the importance-weighted coreset posterior for different coreset sizes (log N, √N, N/2) and dataset sizes N. The results are shown for both basic importance weighting and importance weighting with post-hoc optimal scaling, and for two different models (Cauchy location and logistic regression).

In-depth insights

#

Coreset Bounds

#

The concept of coreset bounds is crucial for evaluating the effectiveness of coreset methods in approximating large datasets. Lower bounds reveal fundamental limitations, highlighting the minimum coreset size required for a certain approximation quality. This is insightful as it helps determine whether a coreset approach is even feasible for a given problem. Upper bounds, on the other hand, provide guarantees on the quality of the approximation achievable with a given coreset size. They’re useful for designing and analyzing coreset construction algorithms, helping to establish convergence rates. The gap between lower and upper bounds indicates the potential for improvement in coreset techniques. The practicality of coresets hinges on finding efficient algorithms that achieve upper bounds close to lower bounds. A significant contribution is often establishing bounds under more relaxed conditions (e.g., weaker than strong log-concavity) and analyzing their applications to real-world Bayesian inference tasks, particularly those with complex posterior distributions.

Importance Weight

#

Importance weighting, a core concept in the paper, addresses the challenge of efficiently approximating a full dataset’s log-likelihood function using a smaller weighted subset. The method’s effectiveness hinges on the careful selection of weights, balancing the need for accurate approximation with computational efficiency. The paper reveals that common importance-weighted coreset constructions require a coreset size proportional to the dataset size, offering negligible improvement over full-data inference, which is a crucial limitation. This finding is theoretically justified by the derivation of asymptotic lower bounds on coreset approximation error, highlighting fundamental limitations. Despite its simplicity and intuitive appeal, the theoretical analysis exposes inherent weaknesses when using importance weighting in constructing Bayesian coresets. Post-hoc optimal weight scaling, while seemingly improving the accuracy, still does not overcome the fundamental limitation of needing a coreset size proportional to the original dataset size. The authors’ analysis sheds light on the practical challenges associated with importance weighting methods, advocating for alternative approaches, specifically, subsample-optimize methods, that demonstrate superior efficiency and scalability for achieving high-quality posterior approximations.

Subsample Optimize

#

The subsample-optimize approach for constructing Bayesian coresets is a powerful technique that addresses limitations of previous methods. It cleverly combines the advantages of subsampling, which reduces computational cost by focusing on a smaller subset of data, with optimization, to refine the weights assigned to the selected data points. This dual strategy avoids the limitations of simpler importance-weighted coresets, which often require coreset sizes proportional to the full dataset, hindering scalability. By first subsampling and then optimizing weights, the method allows for flexibility in choosing a basis for approximation and avoids the issues of biased estimation inherent in purely importance-weighted schemes. Subsample-optimize coresets demonstrably achieve asymptotic error bounds with coreset sizes that grow polylogarithmically with the dataset size, a significant improvement over previous methods. This makes the method particularly suitable for large-scale Bayesian inference problems, where computational cost is a major concern. The theoretical results are validated empirically, demonstrating superior performance even in models with complex features like multimodality or heavy-tailed distributions, showcasing the versatility and effectiveness of this sophisticated approach.

Asymptotic Analysis

#

This research paper delves into the asymptotic analysis of Bayesian coresets, focusing on the behavior of coreset approximations as the dataset size grows infinitely large. A key aspect is the investigation of Kullback-Leibler (KL) divergence, a measure of the difference between the true posterior distribution and its coreset approximation. The analysis establishes general upper and lower bounds on KL divergence, relaxing strong assumptions made in previous works. These bounds reveal fundamental limitations on coreset quality for various models, providing insights into the performance of different coreset construction methods. Importantly, the analysis goes beyond exponential family models and models with strong log-concavity, handling a wider range of model complexities. The theory is supported by empirical validations on multimodal and heavy-tailed models, demonstrating its applicability to complex, real-world problems. The asymptotic analysis offers a powerful tool to theoretically understand the performance of coresets in large-scale Bayesian inference and guide the development of better coreset construction methods.

Future Research

#

Future research directions stemming from this work could significantly advance Bayesian coresets. Improving the theoretical bounds presented here is crucial; the current approach necessitates case-by-case analysis for critical quantities like subexponentiality constants and alignment probabilities. Developing more efficient algorithms that circumvent these limitations is a high priority. Exploring alternative coreset constructions beyond importance weighting and subsample-optimize methods, such as those leveraging dimensionality reduction or novel optimization techniques, could yield substantial improvements in efficiency and accuracy. Furthermore, extending the theoretical framework to encompass broader classes of Bayesian models, including those with intricate dependencies or non-standard priors, would dramatically expand the practical applicability of Bayesian coresets. Finally, rigorous empirical evaluations on diverse, large-scale datasets are needed to validate theoretical findings and guide further algorithm development, particularly focusing on the robustness of coresets in high-dimensional or complex data scenarios.

More visual insights

#

More on figures

This figure empirically validates Corollaries 4.1 and 4.2 which discuss the minimum coreset size for importance-weighted coresets. It shows the minimum KL divergence (a measure of the difference between the true and approximate posterior distributions) plotted against the dataset size (N) for three different coreset sizes (log N, √N, and N/2). The figure presents results for both basic importance-weighted coresets and those with optimal post-hoc scaling, and for two different Bayesian models (Cauchy location and logistic regression). The dashed lines represent theoretical predictions, while the solid lines show the empirical means from 10 trials. Error bars illustrate the standard errors.

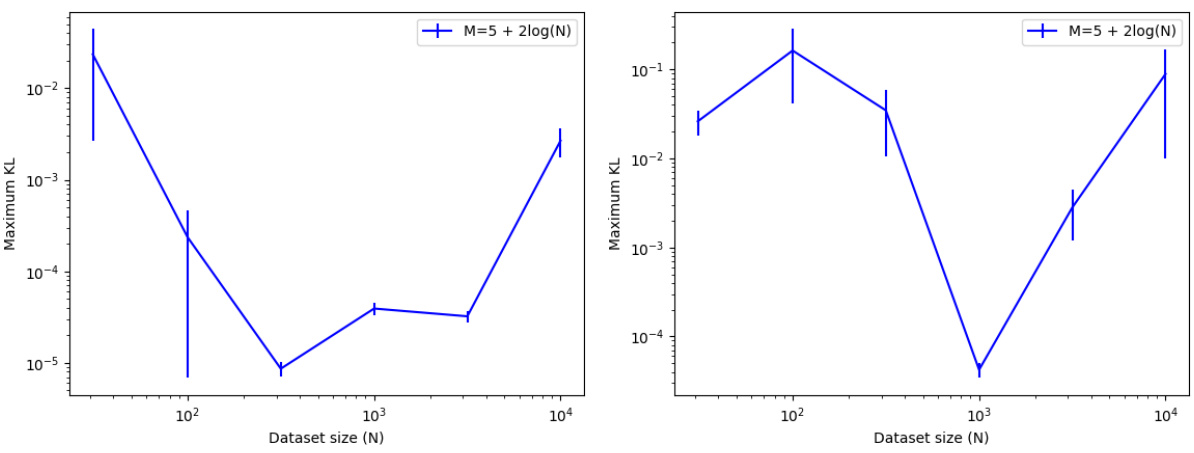
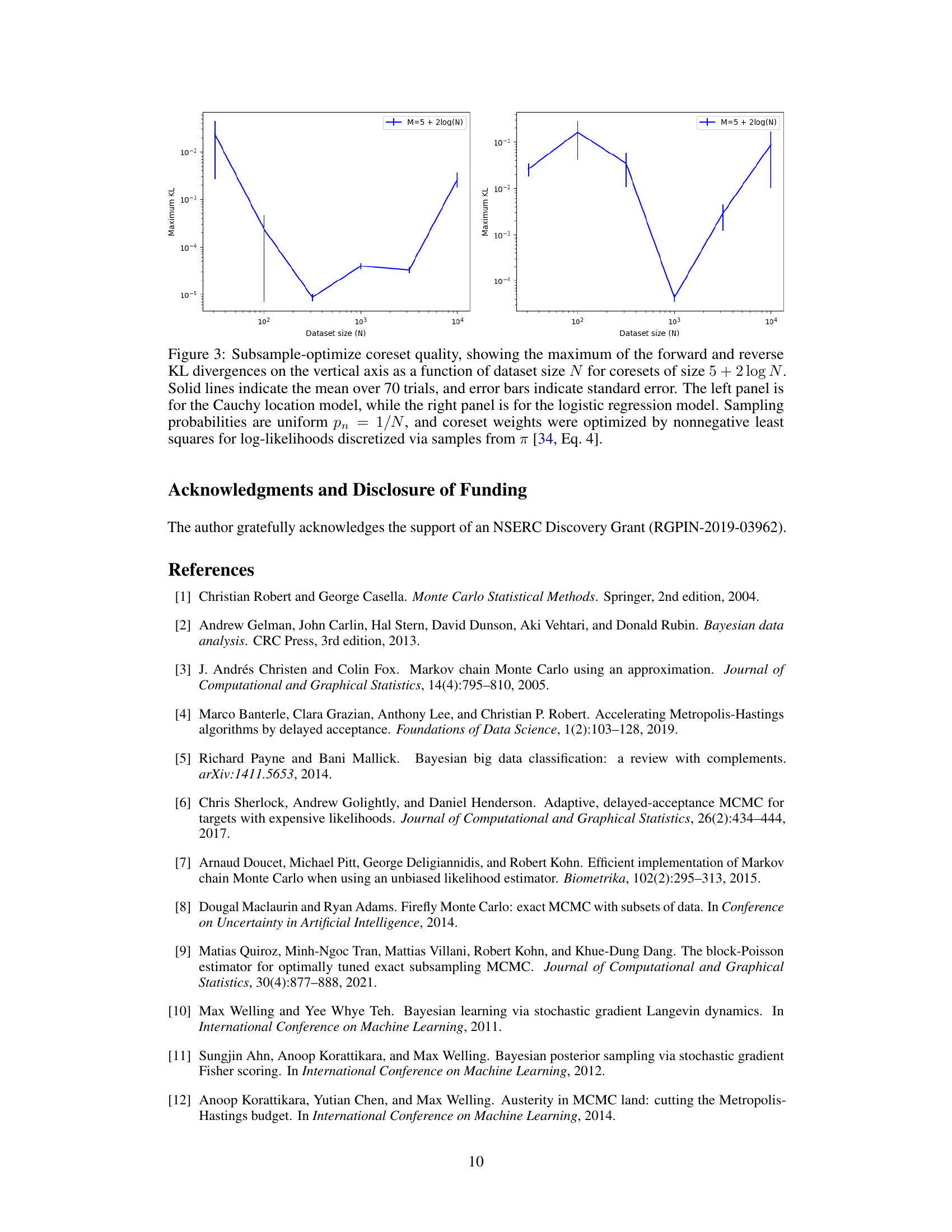
This figure shows the performance of subsample-optimize coreset construction methods on two Bayesian models: a Cauchy location model and a logistic regression model. It displays the maximum KL divergence (a measure of approximation error) between the true posterior and the coreset approximation as a function of the dataset size (N). The coreset size (M) is fixed at 5 + 2log(N). The results demonstrate that high-quality posterior approximations can be achieved with relatively small coresets, even when the models violate common assumptions used in previous theoretical work. Results are averages of 70 trials, with error bars representing standard error.

Full paper

#