Scalable Optimization in the Modular Norm

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in deep learning because it offers a novel solution to the scalability issues of existing optimizers. By introducing the modular norm, it provides a framework for transferring learning rates across different network scales. This solves a major problem that hinders efficient and stable training of large models, opening exciting avenues for further research.

Visual Insights

#

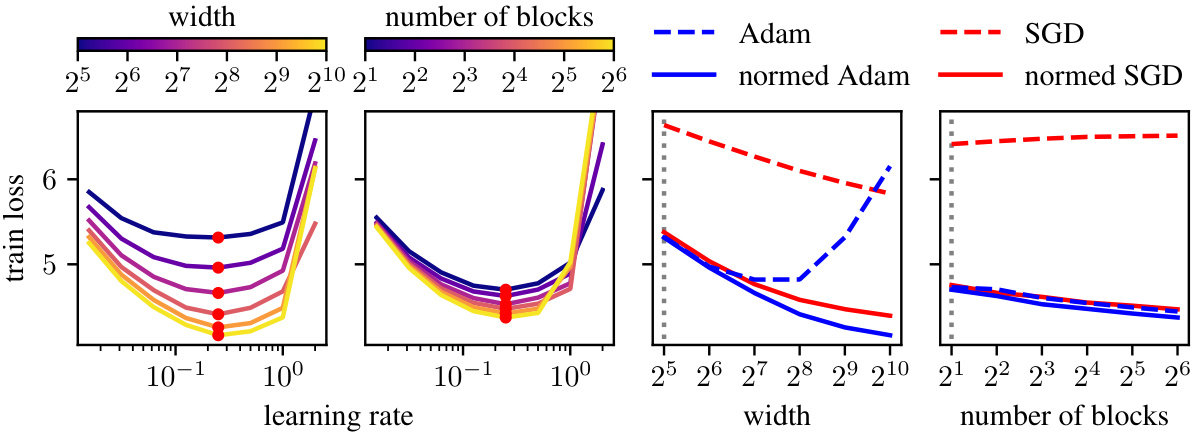
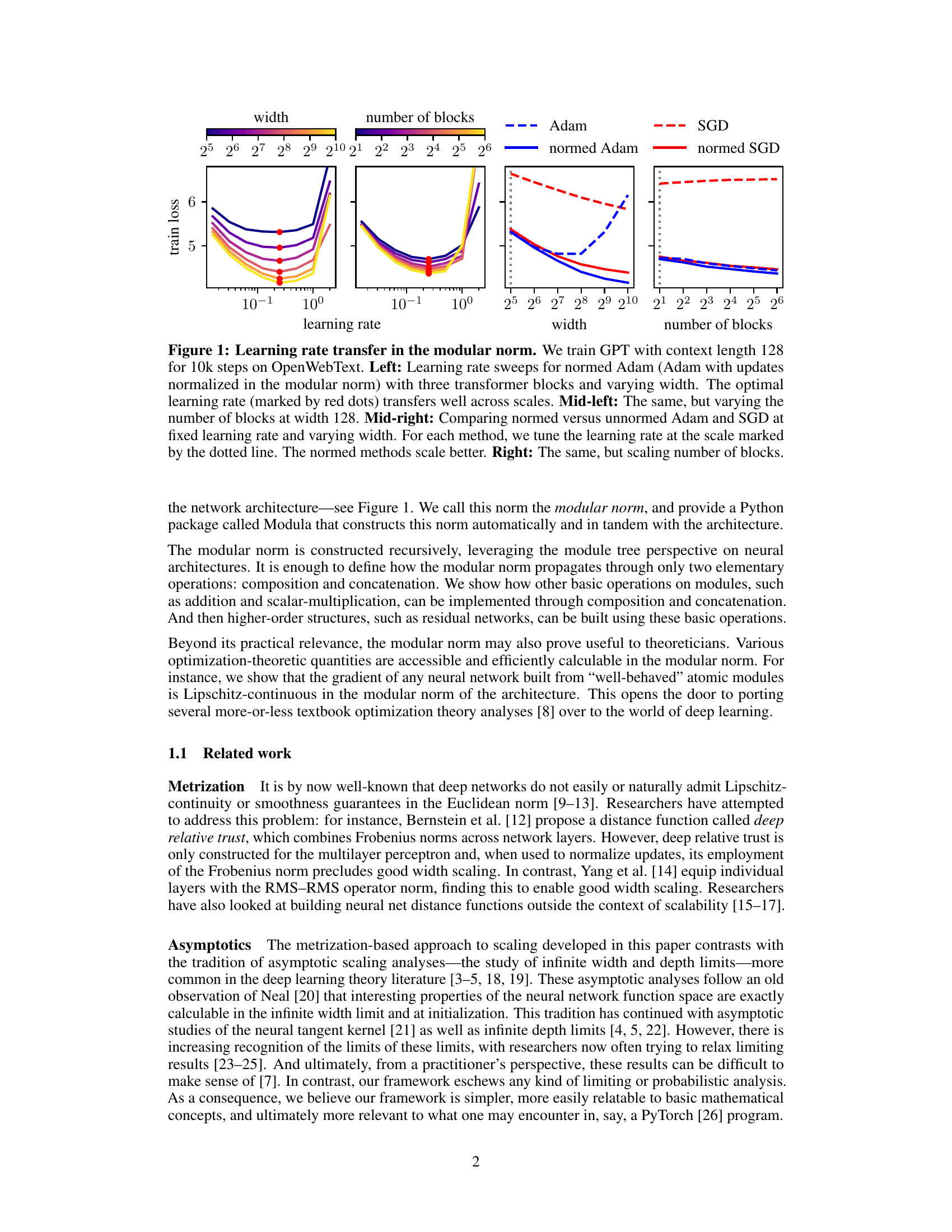
This figure demonstrates the effectiveness of the modular norm in enabling learning rate transfer across different network scales. The plots show training loss curves for various optimizers (Adam and SGD, both with and without modular norm normalization) while varying the width and depth of a GPT model trained on OpenWebText. The consistent optimal learning rates across scales highlight the modular norm’s ability to improve the scalability and stability of training.

This table describes how basic arithmetic operations (addition, scalar multiplication, and iterated composition) can be extended to work with modules. It shows the shorthand notation, formal definition, and Modula expression for each operation. The utility modules mentioned (Add, Mula, Identity) are further explained in Appendix B.2 of the paper.

In-depth insights

#

Modular Norm

#

The concept of a “Modular Norm” in the context of deep learning optimization presents a novel approach to address the challenges of scaling training. It generalizes the idea of weight normalization by defining a norm recursively, mirroring the network’s architecture. This allows for transferability of learning rates across network widths and depths, simplifying the often complex process of hyperparameter tuning for large models. The modular norm’s recursive definition provides a framework for analyzing the Lipschitz continuity of gradients, a key property for understanding optimization dynamics. By normalizing updates within the modular norm, the authors aim to improve the scalability and stability of training, potentially obviating the need for optimizer-specific learning rate adjustments that frequently accompany scaling. The creation of the Modula Python package further enhances its practical applicability, enabling researchers to readily incorporate the modular norm into their deep learning workflows.

Normed Optimizers

#

Normed optimizers represent a novel approach to address the challenges of scaling deep learning training. By normalizing weight updates using a layer-specific or network-wide norm, they aim to improve the stability and efficiency of training across varying network widths and depths. This normalization technique offers potential advantages by making learning rates transferable across different network scales, reducing the need for extensive hyperparameter tuning. The proposed modular norm, calculated recursively through the network architecture, offers a generalizable framework for normalization. Further research is needed to explore the impact of different norms and their impact on various network architectures and datasets, as well as to investigate any potential computational overhead associated with the norm computation. The effectiveness of this approach compared to existing techniques is a key area of future exploration.

Scalable Training

#

Scalable training in deep learning addresses the critical challenge of adapting model training to varying network sizes and complexities without requiring extensive hyperparameter retuning. The core issue is maintaining stable and efficient training as the width or depth of a neural network increases. This necessitates strategies that generalize across different scales, avoiding the need for separate optimization procedures for each network size. Effective approaches often involve sophisticated normalization techniques applied to both weights and gradients, ensuring that the learning process remains robust and efficient irrespective of model scale. Modular norm-based approaches have shown promising results by dynamically adapting the normalization strategy to the network architecture itself, enabling learning rate transferability across different network configurations. This is a key aspect of scalable training as it simplifies the optimization process, improving the efficiency and robustness of training large-scale deep learning models.

Mass Allocation

#

The concept of ‘Mass Allocation’ in the paper presents a novel approach to scaling deep learning models. It introduces mass parameters for each module in the network, controlling the proportion of feature learning each module contributes to the overall model. This approach addresses the challenge of maintaining optimal learning rates across different network widths and depths, offering a significant improvement over ad-hoc learning rate correction methods. The mass parameters allow for a more principled and flexible control of learning dynamics, essentially enabling balanced learning across the modules of any architecture. Theoretical analysis demonstrates the connection between mass allocation and the smoothness of the loss function, further solidifying its importance. The experimental results showcase the effectiveness of this approach across various networks and datasets, demonstrating improved scalability and learning rate transferability. Although the optimal allocation of mass might need to be tuned, the flexibility and intuitive nature of this approach suggests that it could pave the way for more robust and graceful scaling in future deep learning systems.

Future Work

#

The paper’s “Future Work” section implicitly suggests several promising research directions. Improving the efficiency of the normalization process is crucial, potentially through exploring alternative operator norms or leveraging advanced techniques like CUDA-level optimizations. The authors also mention extending the framework to encompass more complex module types beyond the core set used in the experiments. Furthermore, a deeper investigation into the theoretical implications of the modular norm, such as analyzing its properties in non-convex settings, would enhance its applicability in broader deep learning contexts. Finally, the authors express interest in combining the modular norm with existing adaptive learning rate techniques, particularly for robust scaling across different network architectures. Addressing these points would significantly contribute to advancing scalable optimization methods in deep learning.

More visual insights

#

More on figures

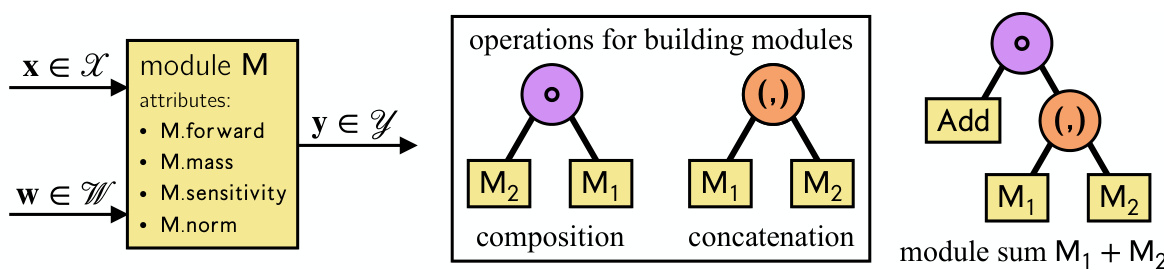
This figure illustrates the concept of modules and how they are combined to form more complex neural networks. The left panel shows a single module with its attributes (forward function, mass, sensitivity, and norm). The middle panel demonstrates how new modules are created through composition and concatenation of existing modules. The right panel depicts a compound module, represented as a binary tree where leaf nodes are individual modules and internal nodes represent the combination operations (composition, concatenation, and addition).

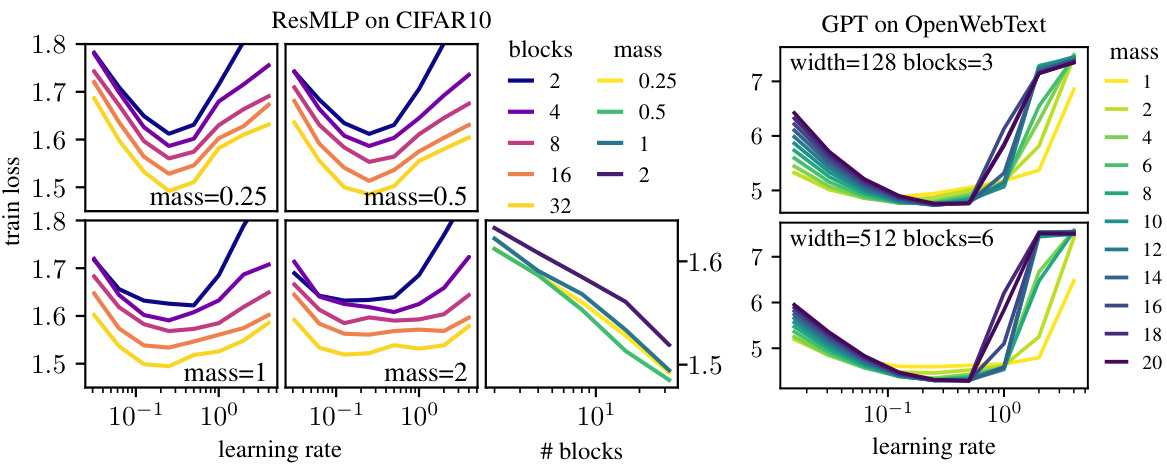
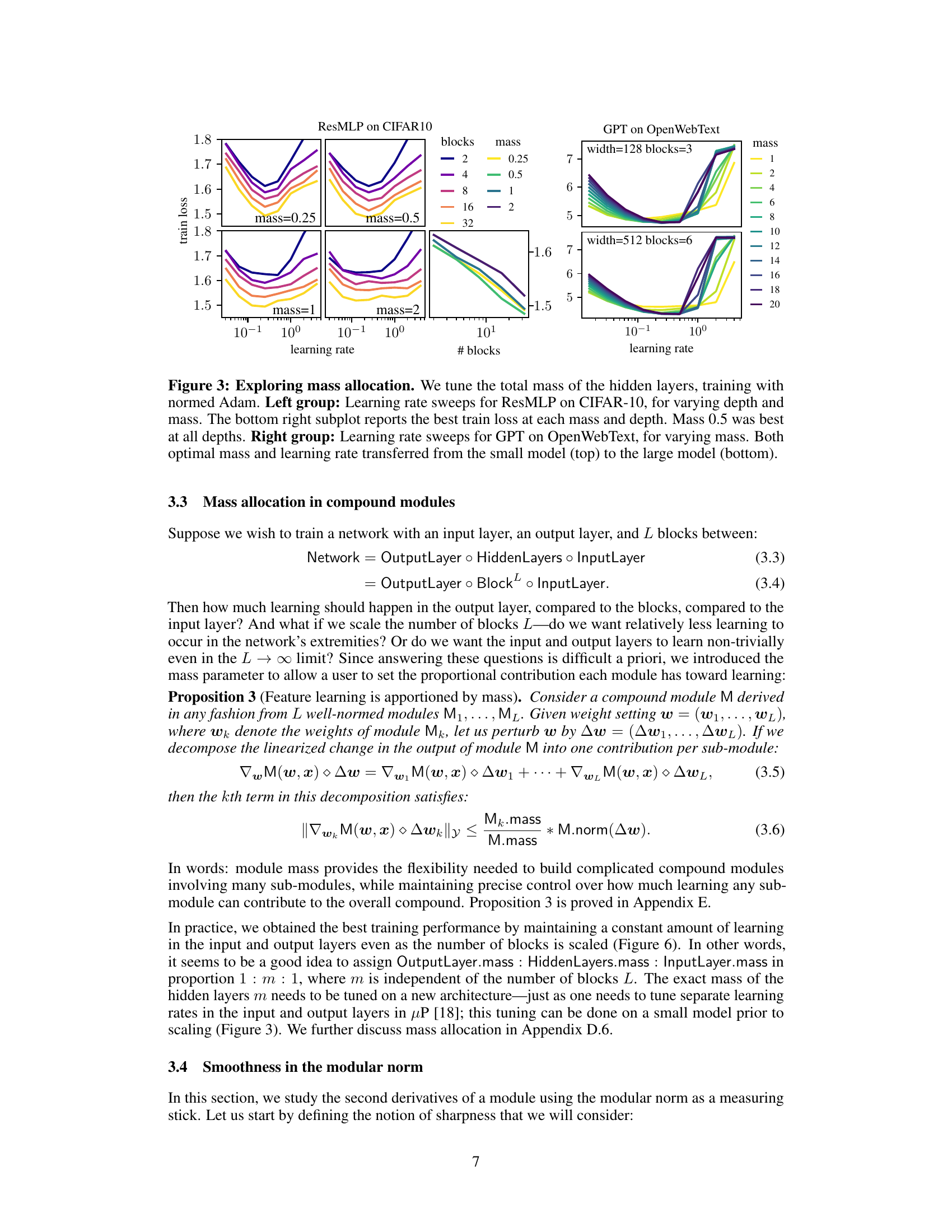
This figure shows the effect of mass allocation on the learning rate and training loss for two different models: ResMLP on CIFAR-10 and GPT on OpenWebText. The left side demonstrates how the optimal mass (controlling the proportion of learning for different layers) affects training loss at various depths for ResMLP. The right side shows how the optimal mass changes the learning rate and training loss for GPT across different scales, demonstrating transferability of the optimal hyperparameters.

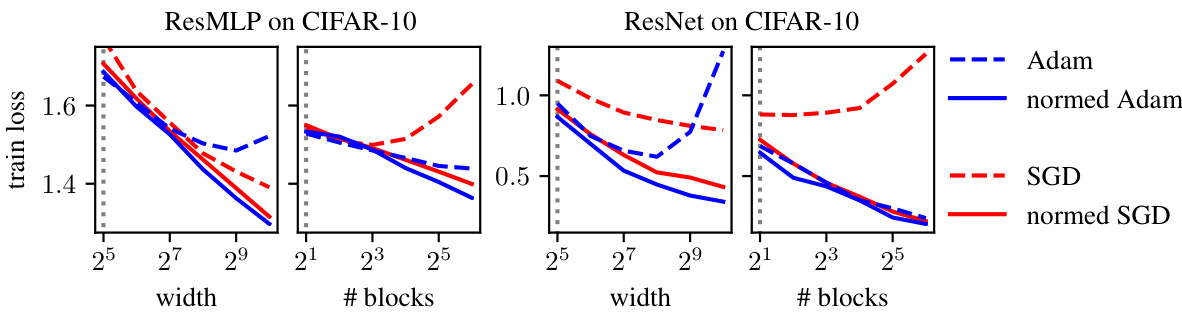
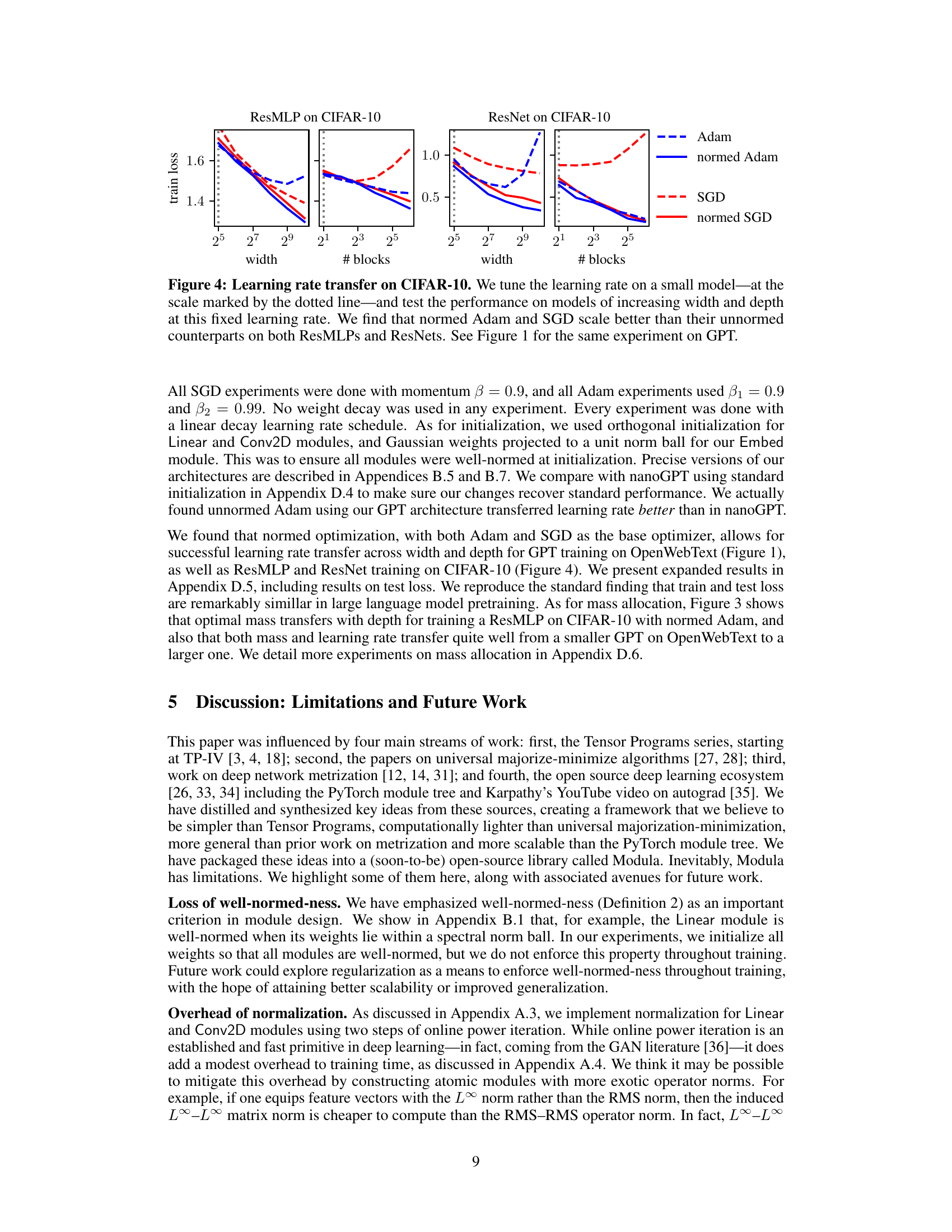
This figure shows the results of an experiment to test the scalability of training with normed Adam and SGD optimizers. The learning rate was tuned on a small model, and then the performance of models with increasing width and depth was tested using that same fixed learning rate. The results demonstrate that the normed Adam and SGD optimizers scale better than their unnormed counterparts on both ResMLP and ResNet models.

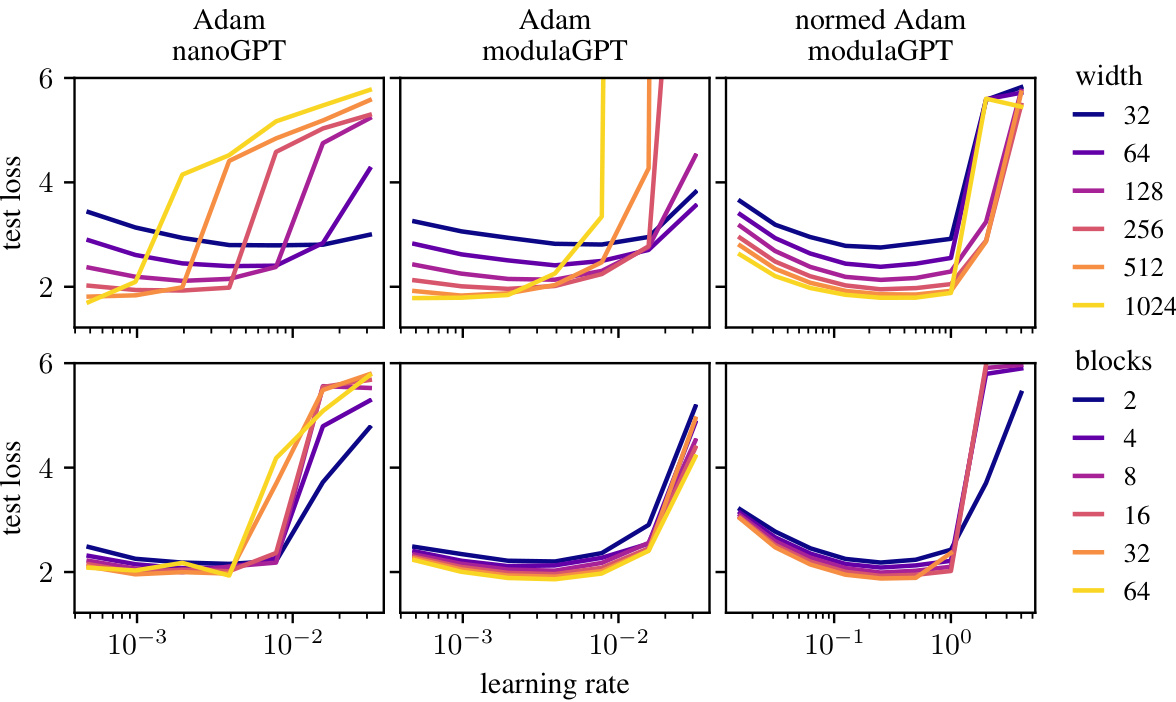
This figure demonstrates the learning rate transferability in the modular norm across different network scales. It shows that normalizing weight updates using the modular norm allows for consistent optimal learning rates across varying network width and depth, unlike standard optimizers such as Adam and SGD. The leftmost panel shows learning rate sweeps for normed Adam with a fixed number of blocks and varying width. The red dots show that the optimal learning rates are consistent across widths. The next panel shows the same experiment, but with varying numbers of blocks. The next panel compares normed versus unnormed Adam and SGD. The final panel shows scaling by number of blocks. In all cases, the modular norm improves the transferability of the learning rate.

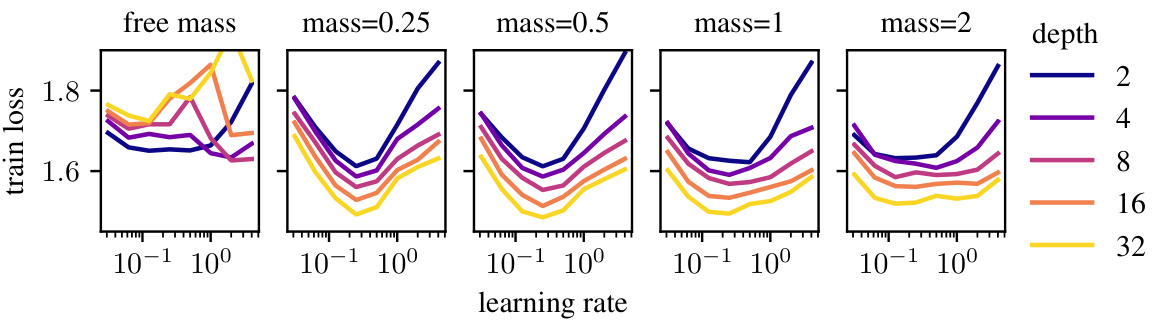
This figure shows the effect of mass allocation on the learning rate in two different models, ResMLP (on CIFAR-10 dataset) and GPT (on OpenWebText dataset). The left side displays learning rate sweeps for ResMLP with varying depth and mass, indicating that a mass of 0.5 consistently yielded the best results across different depths. The right side shows learning rate sweeps for GPT with varying mass; the optimal mass and learning rate are transferable from smaller to larger models, highlighting the transferability aspect of the modular norm.

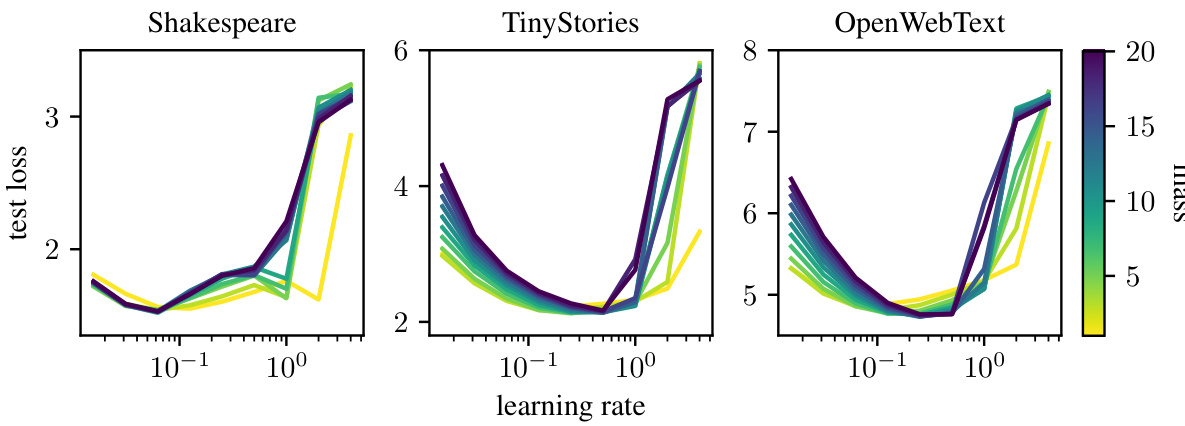
This figure displays the results of training a small GPT model (width 128, 3 blocks) on three datasets of increasing size and complexity: Shakespeare, TinyStories, and OpenWebText. The experiment swept across different learning rates and total masses assigned to the model’s blocks. The results show that optimal learning rates and masses transfer well between TinyStories and OpenWebText (similar in size and complexity), but less so when transferring from the much smaller Shakespeare dataset.

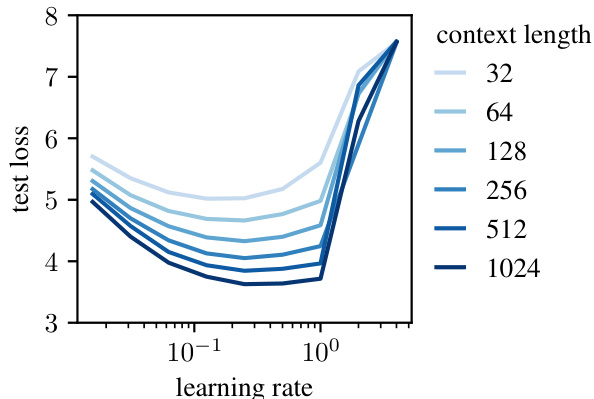
This figure shows the results of training GPT models with different context lengths using the normed Adam optimizer. The x-axis represents the learning rate used during training, and the y-axis represents the test loss achieved. Each line represents a different context length, ranging from 32 to 1024. The figure demonstrates that the optimal learning rate remains relatively consistent across different context lengths, supporting the claim that the modular norm allows for better learning rate transfer across various scales.

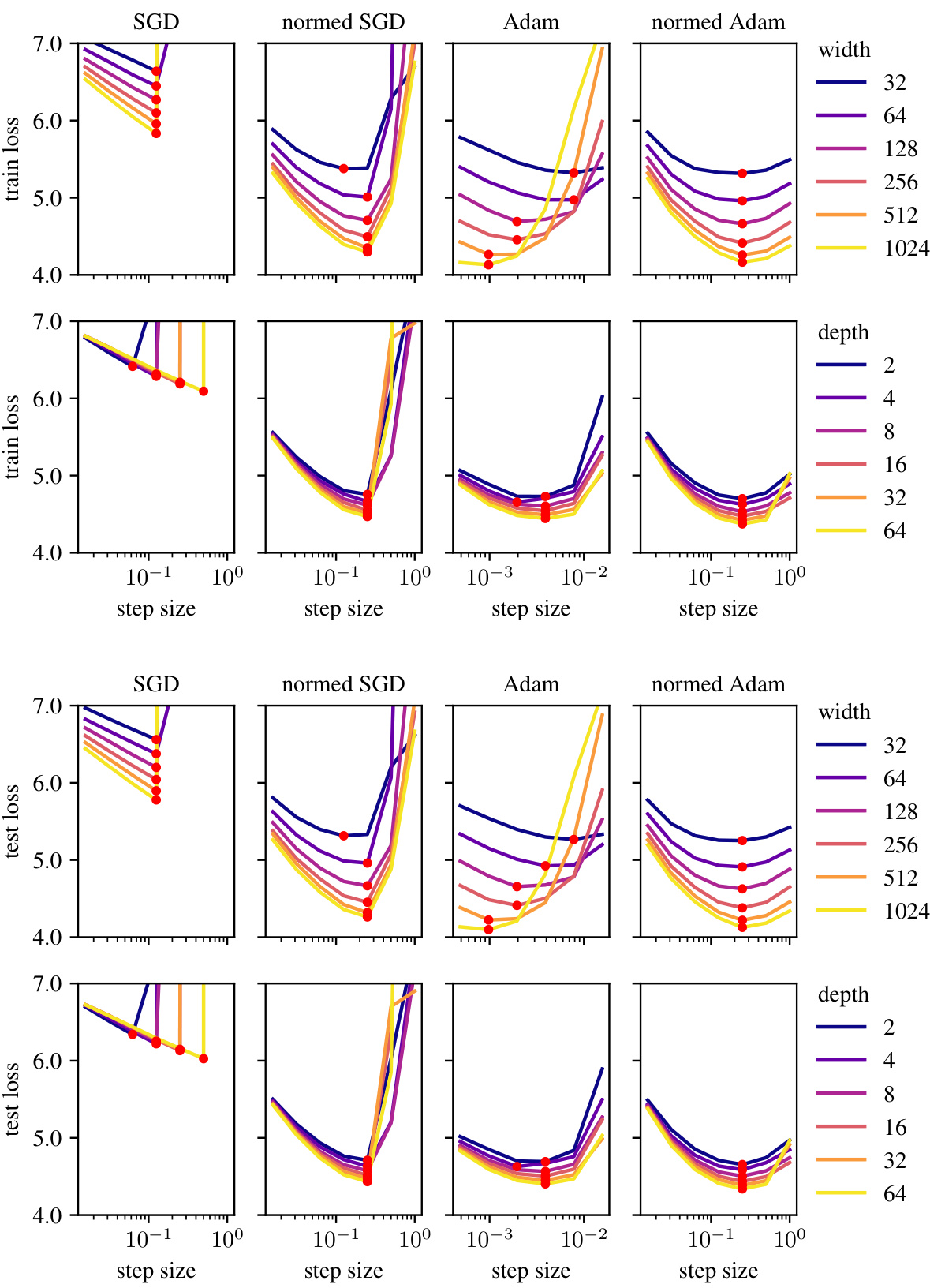
This figure demonstrates the effectiveness of the modular norm in normalizing optimizer updates. It shows that using the modular norm (normed Adam and SGD) allows for consistent optimal learning rates across varying network widths and depths, unlike the unnormalized versions (Adam and SGD). The optimal learning rate, indicated by red dots, remains relatively stable when scaling either width or depth, highlighting the improved transferability of learning rates achieved through modular norm normalization.

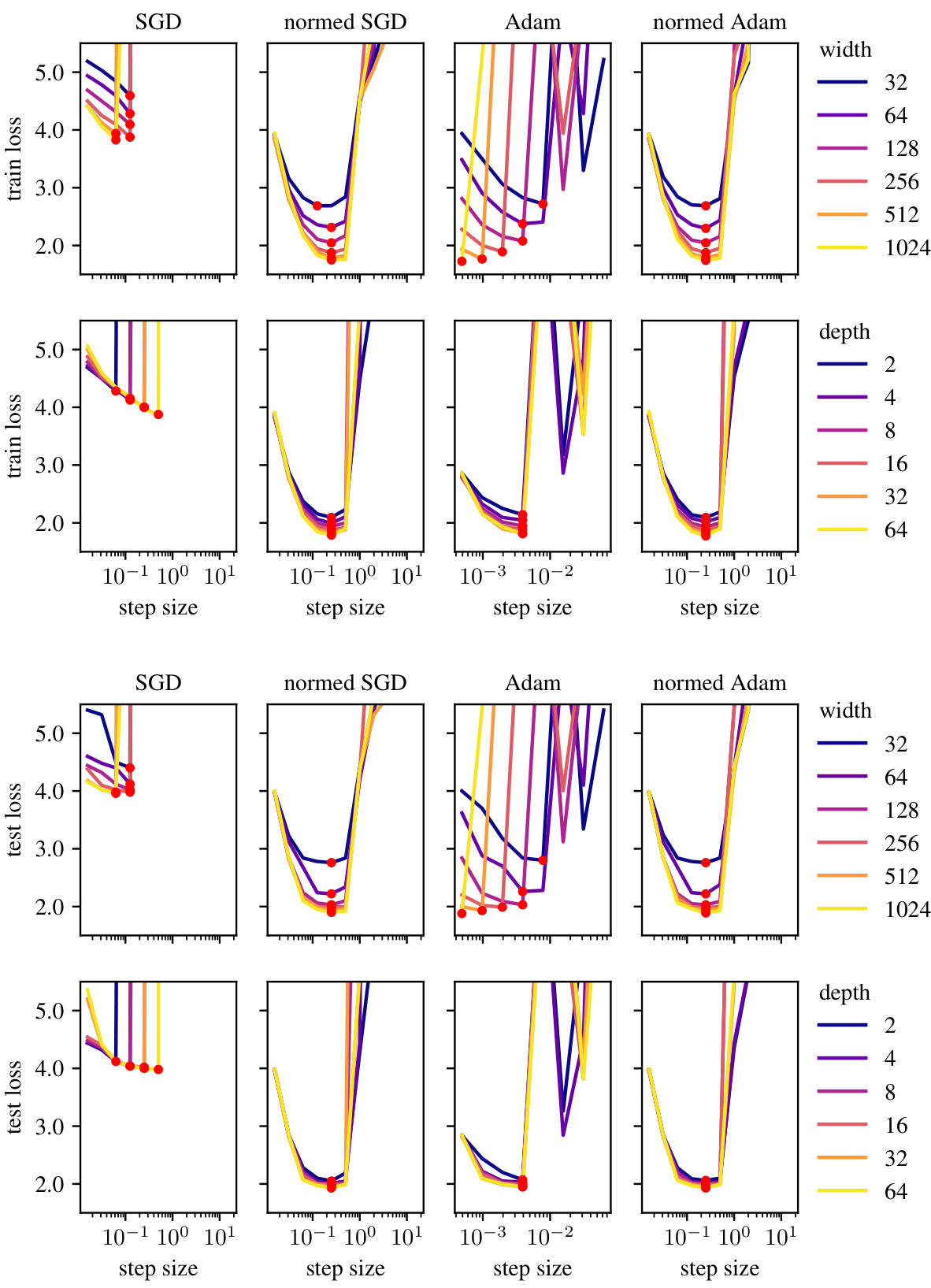
This figure shows the impact of using the modular norm to normalize optimizer updates during the training of a GPT model. Four plots demonstrate that the optimal learning rate remains consistent when varying the width or depth of the model, provided the updates are normalized using the modular norm. This demonstrates the transferability of the learning rate across different model scales and suggests that the modular norm improves the scalability of training compared to traditional optimization methods.

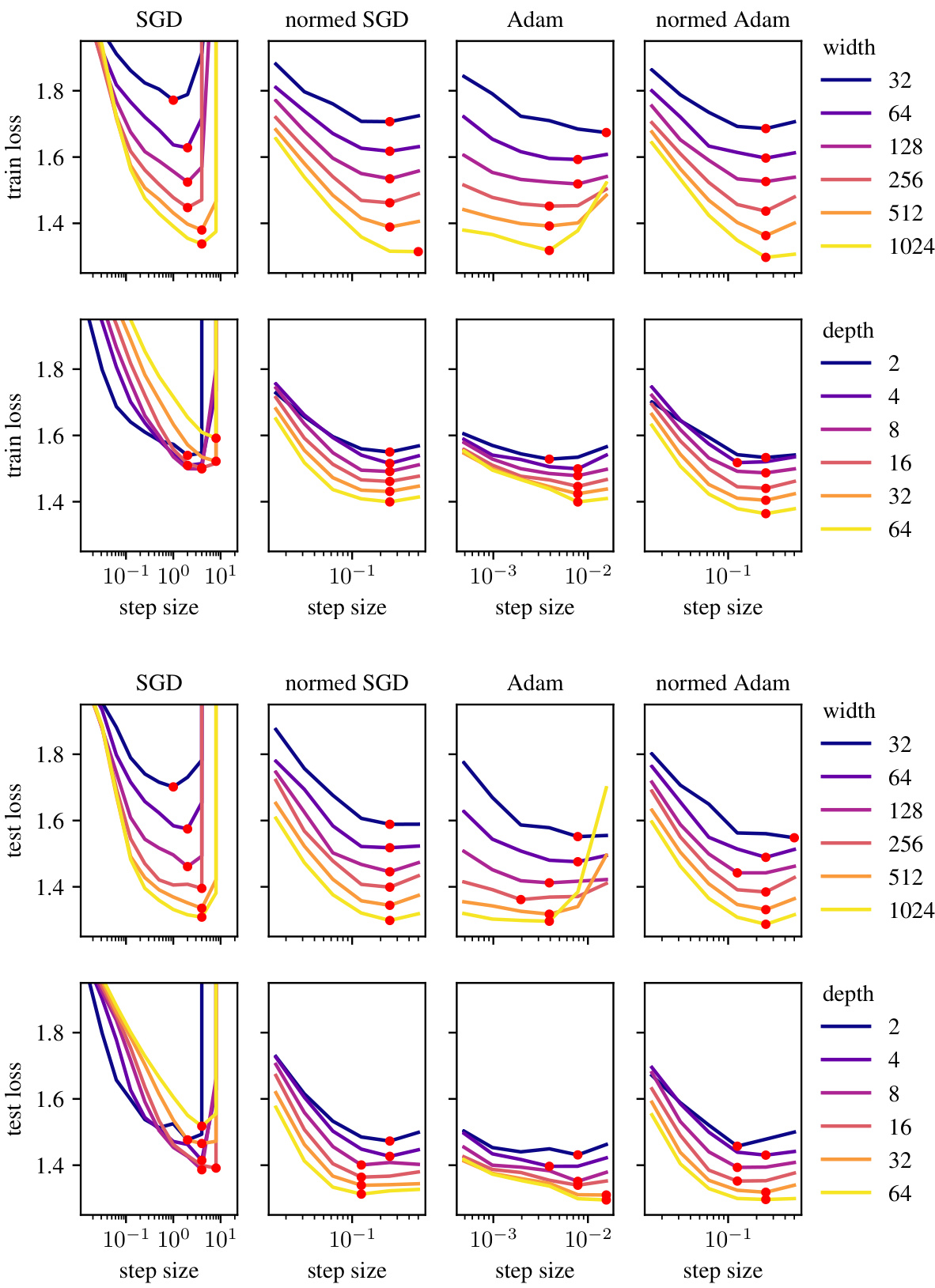
This figure demonstrates the impact of using the modular norm to normalize Adam and SGD optimizers on the transferability of learning rates across different network scales (width and depth). The experiment tunes the learning rate on a smaller model and then evaluates performance on larger models with the same learning rate. Results show that using the modular norm improves the scalability of both Adam and SGD, as compared to their unnormalized counterparts.

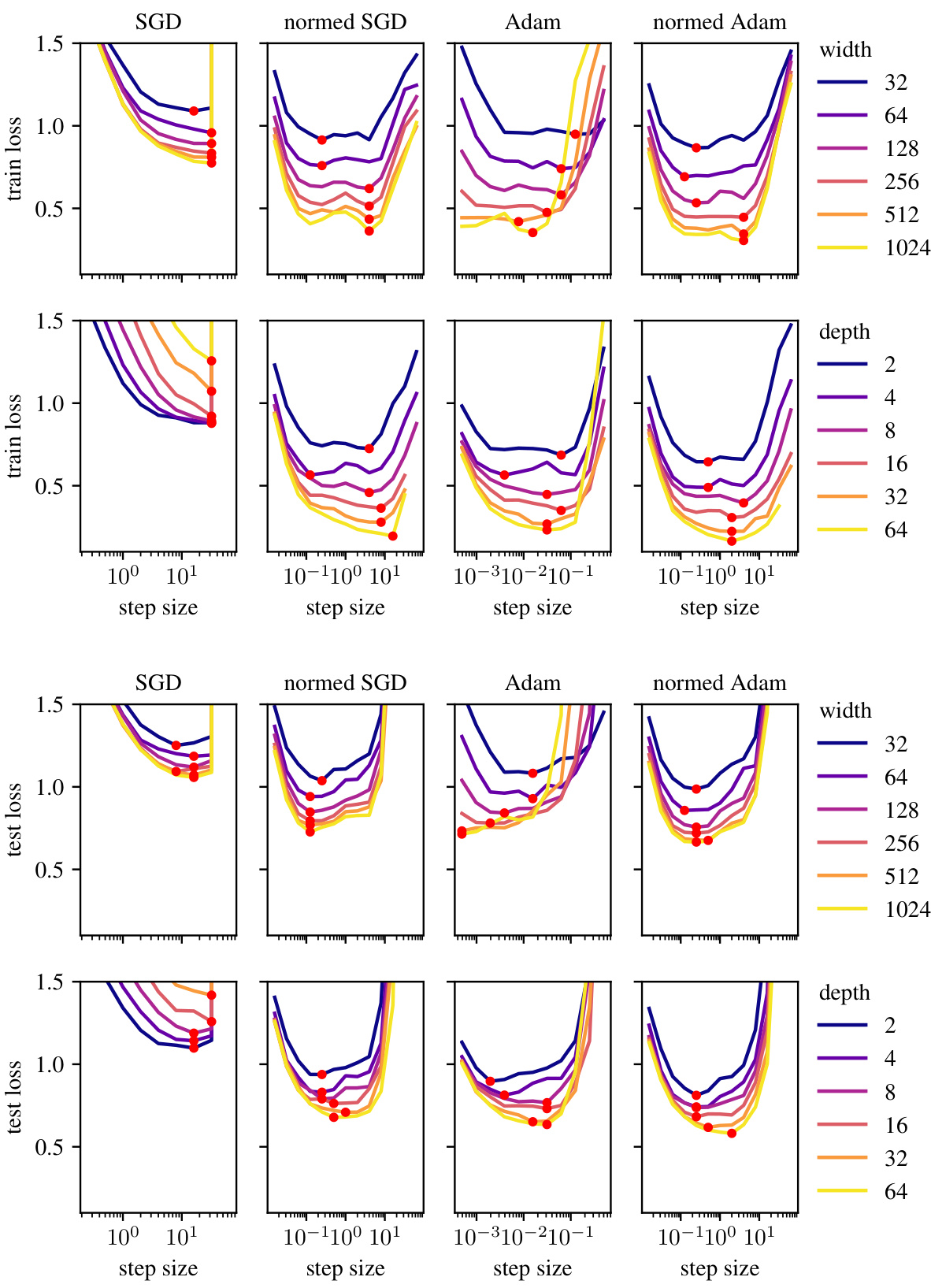
This figure demonstrates the effectiveness of the modular norm in improving the scalability of Adam and SGD optimizers. The learning rate is tuned on smaller models (indicated by a dotted line), and then the performance of those optimizers is tested on models with increasing width and depth, using the same tuned learning rate. The results show that when using the modular norm (i.e., ’normed’ versions), both optimizers significantly outperform their un-normalized counterparts, demonstrating the transferability of the learning rate across different model scales.

Full paper

#