↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Training machine learning models often requires careful tuning of hyperparameters like step size and gradient clipping threshold. This is time-consuming, especially with multiple hyperparameters. Existing parameter-free methods mainly focus on step size optimization, leaving other hyperparameters untouched. This paper tackles this problem.
The paper proposes “Inexact Polyak Stepsize,” a novel parameter-free method for clipped gradient descent. This method automatically adjusts both step size and gradient clipping threshold during training, converging to optimal solutions without manual tuning. The convergence rate is shown to be asymptotically independent of the smoothness parameter L, similar to the rate of clipped gradient descent with well-tuned hyperparameters. Experiments validate the approach, showing its effectiveness on various neural network architectures.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the limitations of existing parameter-free optimization methods by proposing Inexact Polyak Stepsize, a novel approach for clipped gradient descent that automatically adjusts hyperparameters, achieving faster convergence and eliminating the need for manual tuning. This significantly reduces the computational cost of hyperparameter search, which is crucial for large-scale machine learning tasks. The proposed method’s asymptotic independence of L under (L0, L1)-smoothness assumption is a notable theoretical contribution, opening new research avenues in efficient optimization algorithms.
Visual Insights#

This figure compares the convergence behaviors of different optimization methods using a synthetic function. The methods include Gradient Descent, Clipped Gradient Descent, Polyak Stepsize, DecSPS, AdaSPS, and Inexact Polyak Stepsize. The x-axis represents the number of iterations, and the y-axis represents the value of f(x) - f*, which is the difference between the loss function value at the current iteration and the optimal loss value. Each line represents a different optimization method, and different colors represent different values of L1 in the (L0,L1)-smoothness condition. The figure demonstrates that Inexact Polyak Stepsize achieves a convergence rate that is asymptotically independent of L, which is the key property investigated in the paper.

This table shows the hyperparameters (learning rate and gradient clipping threshold) selected by grid search for three different seed values in the experiments using LSTM, Nano-GPT, and T5. The multiple values indicate that the hyperparameter tuning was performed separately for each seed value to account for the randomness in the training process.
In-depth insights#
Polyak Stepsize Boost#
A hypothetical ‘Polyak Stepsize Boost’ section in a research paper would likely explore enhancements to the Polyak stepsize method for gradient descent optimization. This could involve several key areas. First, adaptive strategies could be investigated to dynamically adjust the Polyak stepsize based on the characteristics of the loss function or the gradient’s behavior, potentially improving convergence speed and stability. Second, the exploration of parameter-free variations of Polyak stepsize would be relevant, enabling the algorithm to adapt without requiring manual tuning. Theoretical analysis of any proposed boosts would be crucial, providing insights into convergence rates and their dependence on problem parameters. Finally, empirical validation through experiments on benchmark datasets and machine learning models would demonstrate the effectiveness of the proposed boosts compared to traditional Polyak stepsize and other optimization methods.
Parameter-Free Descent#
Parameter-free descent methods aim to eliminate the need for manual hyperparameter tuning, a significant challenge in traditional gradient descent. This is achieved by dynamically adjusting parameters like step size during training, often using techniques inspired by Polyak’s step size or adaptive methods. The core benefit is improved efficiency and robustness, as the algorithm adapts to the problem landscape without requiring extensive grid searches or expert knowledge. Convergence guarantees for these methods are often established under specific assumptions about the loss function (e.g., convexity, smoothness), and the asymptotic rate of convergence is a key area of analysis. Challenges include ensuring stability and preventing oscillations, which may require careful design of the adaptive mechanisms. The trade-off between parameter-free simplicity and optimal performance remains an area of ongoing research, with the goal of finding parameter-free methods that converge as quickly as optimally tuned gradient descent.
Clipped Gradient Wins#
The heading “Clipped Gradient Wins” suggests a research focus on the effectiveness of clipped gradient descent in training machine learning models. It implies a comparative analysis demonstrating that clipped gradients outperform other gradient-based optimization techniques. The “wins” likely refer to superior performance metrics, perhaps faster convergence rates, improved stability, or better generalization capabilities. The research likely explores scenarios where the benefits of clipped gradients are most pronounced, such as those involving exploding gradients or highly sensitive loss functions. A key aspect would be the investigation of different clipping strategies and their effects on model performance and training dynamics. The paper would likely explore the trade-offs involved—clipping might impede convergence speed in certain cases. A theoretical analysis could provide insights into the conditions under which clipped gradients guarantee better results, and empirical results would validate the claims on various benchmark datasets and model architectures. Ultimately, the paper should offer a robust argument supported by both theoretical justification and practical evidence to confirm the efficacy of clipped gradient descent.
Inexact Polyak Edge#
The concept of “Inexact Polyak Edge” suggests a modification to the Polyak step size method in gradient descent optimization. The “inexact” aspect likely refers to using an approximation of the optimal solution or a lower bound for the minimum loss value, thereby removing the dependence on precise, problem-specific parameters. This approach aims to achieve a convergence rate that is asymptotically independent of the Lipschitz smoothness constant (L) while maintaining the favorable convergence properties of Polyak step size, particularly under (L0, L1)-smoothness assumptions. The “edge” might imply a superior convergence rate compared to existing parameter-free methods. Such an approach would provide a more robust and efficient optimization technique, particularly beneficial for training complex machine learning models. This method would be especially valuable for large-scale applications where precise parameter tuning is computationally expensive and impractical. The key challenge would lie in balancing the inexactness of the approximation with the need to maintain fast convergence.
(L0,L1)-Smooth Analysis#
(L0,L1)-smooth analysis offers a refined perspective on the smoothness of a function, moving beyond the traditional L-smooth assumption. It acknowledges that the Lipschitz constant of the gradient might vary significantly across different regions of the function’s domain. By introducing two parameters, L0 and L1, (L0,L1)-smoothness captures this nuanced behavior, where L0 represents the local Lipschitz constant and L1 scales with the gradient norm. This is particularly useful in scenarios where the gradient norm is small near optima, leading to faster convergence rates than those predicted under the simpler L-smooth assumption. The (L0,L1) framework is especially relevant for deep learning, where the gradient’s magnitude can fluctuate dramatically during training, and gradient clipping is often employed to enhance stability. It provides a more realistic and rigorous foundation for analyzing such scenarios and can greatly improve theoretical convergence results. Importantly, it allows for better understanding of gradient clipping, showing how it improves convergence rates by utilizing the smaller local Lipschitz constant. Therefore, this analysis offers a significant contribution to the theoretical underpinnings of optimization algorithms and sheds light on the efficacy of commonly used techniques such as gradient clipping.
More visual insights#
More on figures

This figure displays the final test loss achieved by several different optimization methods across three neural network architectures: LSTM, Nano-GPT, and T5. Each method was tested with a range of step sizes. For T5, DecSPS and AdaSPS results were excluded due to significantly higher test loss than other methods; results for SGD were also excluded in cases where the loss reached NaN or infinity. The figure helps to compare the performance of various algorithms under different hyperparameter choices and highlights the impact of hyperparameters on the final model performance.

This figure compares the convergence behaviors of different optimization methods using a synthetic function. The x-axis represents the number of iterations, and the y-axis represents the loss function value. The methods being compared include Gradient Descent, Clipped Gradient Descent, Polyak Stepsize, DecSPS, AdaSPS, and Inexact Polyak Stepsize. The figure demonstrates that Inexact Polyak Stepsize is less sensitive to the hyperparameter L1 compared to other methods.

The figure shows the convergence behaviors of various methods on a synthetic function. The methods compared include gradient descent, clipped gradient descent, Polyak stepsize, DecSPS, AdaSPS, and Inexact Polyak Stepsize. The x-axis represents the number of iterations, and the y-axis represents the difference between the loss function value and the optimal value. The figure demonstrates that the convergence rates of Polyak stepsize, DecSPS, and AdaSPS degrade as L1 increases. In contrast, the convergence behavior of Inexact Polyak Stepsize does not depend on L1, which is consistent with Theorem 5. Inexact Polyak Stepsize successfully inherits the favorable properties of Polyak Stepsize under (L0,L1)-smoothness.

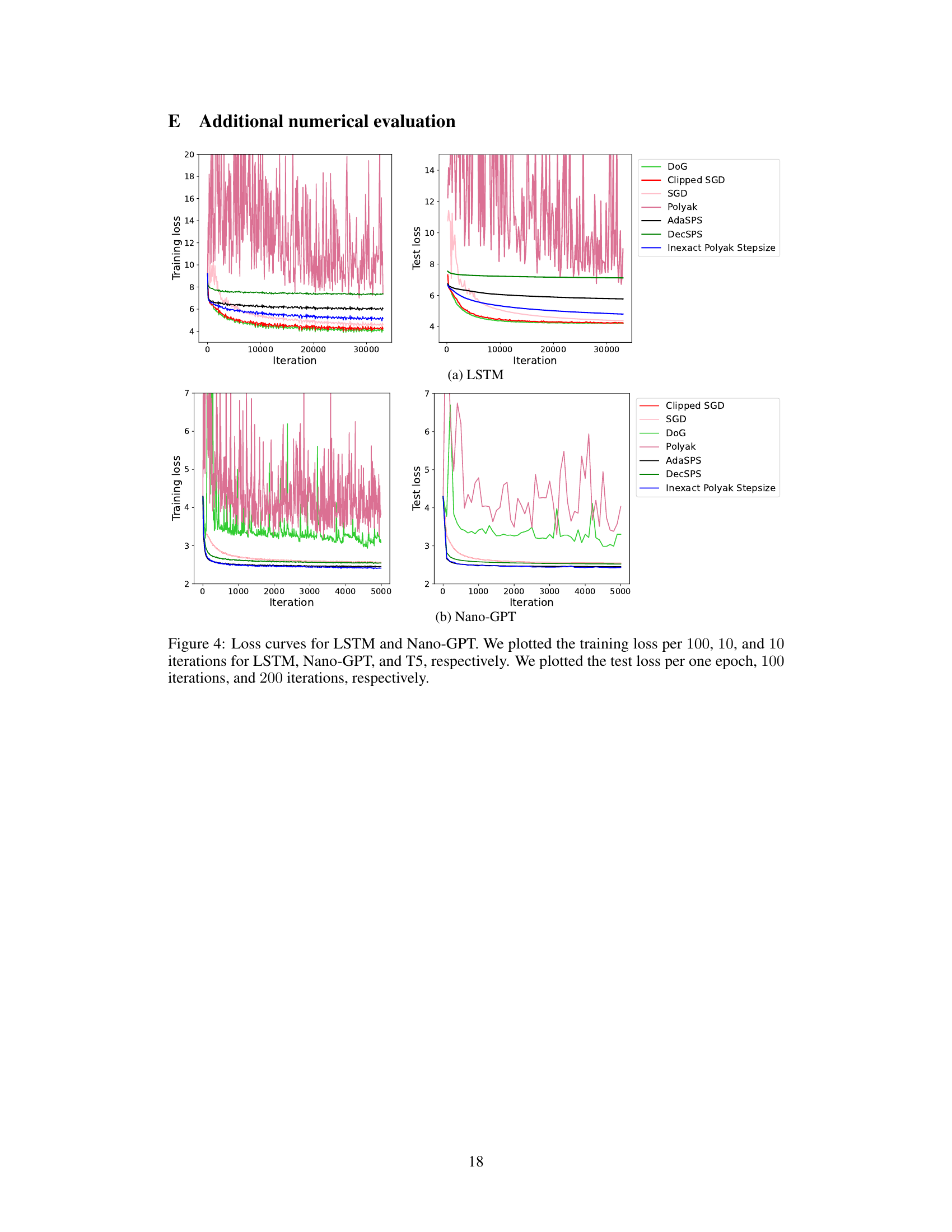
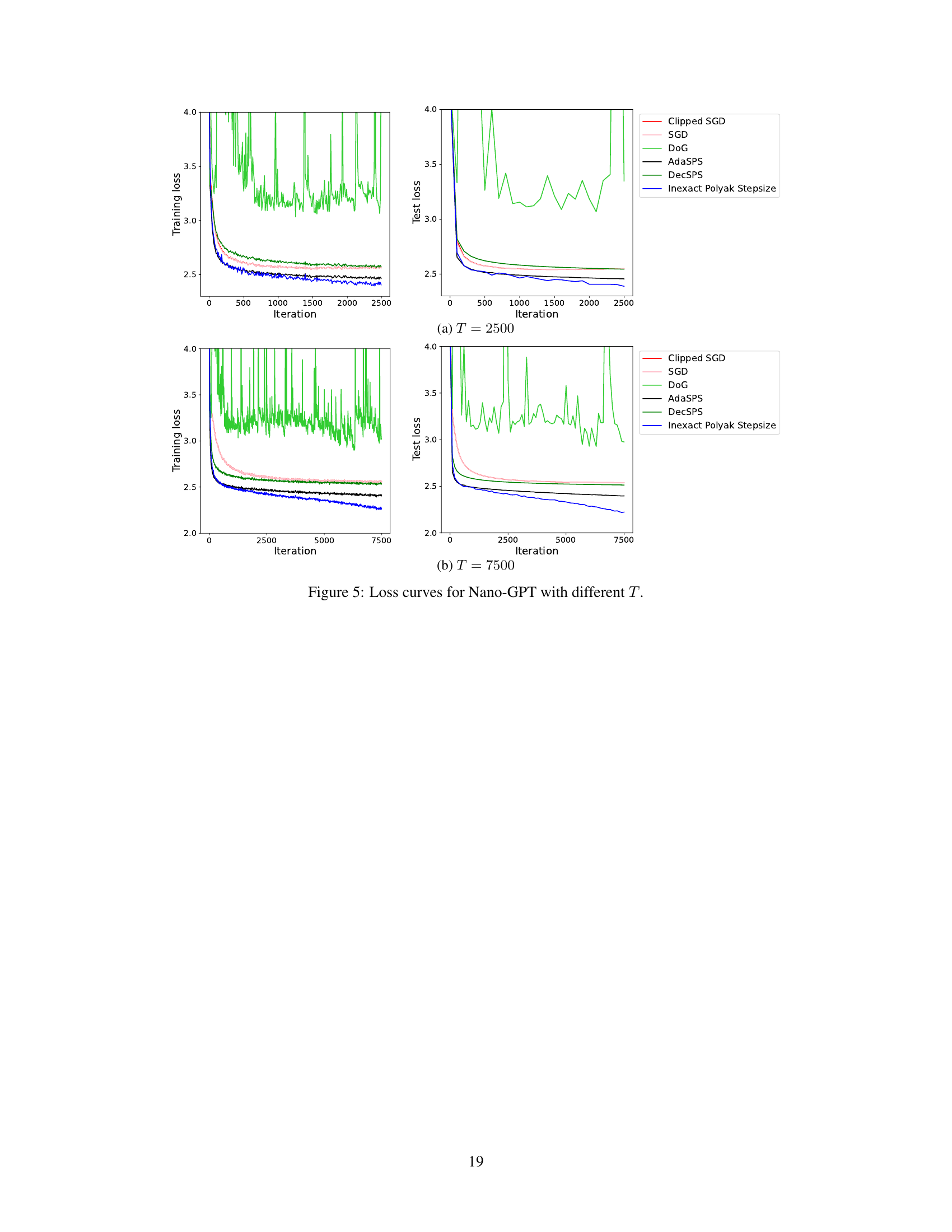
This figure shows the training and test loss curves for the Nano-GPT model trained with different numbers of iterations (T=2500 and T=7500). It compares the performance of various optimization methods, including Clipped SGD, SGD, DoG, AdaSPS, DecSPS, and the proposed Inexact Polyak Stepsize. The plot helps to visualize how the different algorithms converge (or fail to converge) to a solution over time, especially highlighting the effects of the number of iterations on the convergence behavior and the relative performance of Inexact Polyak Stepsize.
More on tables

This table summarizes the convergence rates of three parameter-free methods (DecSPS, AdaSPS, and Inexact Polyak Stepsize) based on the Polyak stepsize. It shows the convergence rate achieved by each method under different assumptions (L-smoothness for DecSPS and AdaSPS, and (L0, L1)-smoothness for Inexact Polyak Stepsize) about the loss function. The convergence rates are expressed in terms of the number of iterations (T), the smoothness parameters (L, L0, L1), and the distance to the optimum (DT, ||x0 - x*||). Note that the convergence rate of Inexact Polyak Stepsize is asymptotically independent of L under (L0, L1)-smoothness, a key advantage highlighted in the paper.

This table shows the range of hyperparameters used for the clipped gradient descent experiments in the paper. The hyperparameters that were tuned are the learning rate and the gradient clipping threshold. The learning rate was varied over several orders of magnitude, while the gradient clipping threshold was tested with various fixed values and also the case where no clipping was applied (infinity).

This table presents the hyperparameters selected through grid search for both gradient descent and clipped gradient descent methods. The hyperparameters considered were the learning rate and the gradient clipping threshold (for the clipped gradient descent). Four different values for L1 (a parameter related to the smoothness of the loss function) were tested: 1, 10, 100, and 1000. The learning rates and clipping thresholds shown in the table were chosen as optimal during the experiment for each of the values of L1.

This table displays the hyperparameter settings used for training the LSTM model. It shows the range of learning rates explored, the gradient clipping thresholds tested, and the batch size used during training. These settings were used in a grid search to find optimal hyperparameters for the LSTM model.

This table presents the hyperparameter settings used for gradient descent and clipped gradient descent experiments in the paper. Three values are given for each hyperparameter, representing the settings used with three different random seeds. The table is broken down by model (LSTM, Nano-GPT, T5) and shows the learning rate used for both gradient descent and clipped gradient descent, as well as the gradient clipping threshold used for the clipped gradient descent method.
Full paper#