↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current methods for verifying the safety of neural network controllers are limited by the complexity of neural networks, the need for unbounded time horizons and the lack of tools capable of handling nonlinear properties. This paper introduces VerSAILLE, which integrates differential dynamic logic (a formal verification technique) with neural network verification tools to address these issues. By creating a verifiable “control envelope” that specifies safe system behavior, VerSAILLE ensures that the neural network controller adheres to these safety constraints. This overcomes limitations of previous approaches which often relied on time bounds or approximations that do not guarantee infinite-time safety.
The paper also introduces Mosaic, a novel technique that overcomes the computational challenges of verifying nonlinear properties. Mosaic effectively partitions the verification task into smaller, more manageable subproblems and lifts the capabilities of existing linear constraint tools to the nonlinear setting. The combination of VerSAILLE and Mosaic allows for the verification of complex, real-world systems such as the Vertical Airborne Collision Avoidance (ACAS) system, demonstrating the practical applicability of the approach. Both VerSAILLE and Mosaic significantly enhance the capacity to formally verify the safety of systems relying on neural networks.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on neural network control systems (NNCSs) because it presents VerSAILLE, a novel framework that allows reusing control theory literature for NNCS verification, and Mosaic, an efficient technique for verifying complex NN properties, pushing the boundaries of what’s achievable with existing tools. The work addresses the critical need for proving the safety of autonomous systems based on neural networks, enabling their safe deployment in real-world applications. This approach is significant for developing trustworthy AI systems and opens new avenues for research in formal verification and NNCS safety.
Visual Insights#
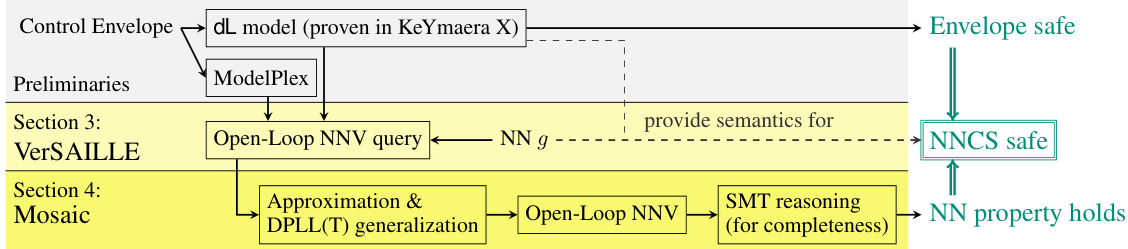
This figure illustrates the VerSAILLE approach which uses a control envelope proven in differential dynamic logic (dL) to verify infinite-time safety of a neural network controlled system (NNCS). It shows how open-loop neural network verification (NNV) is used to check if the neural network adheres to the control envelope, effectively transferring the dL safety guarantee to the NNCS. The figure also highlights the Mosaic technique that extends the applicability of existing linear-constraint open-loop NNV tools to polynomial constraints, enabling the verification of NN properties with arbitrary logical structure.

This table presents the applicability of the research results to different classes of neural networks (NNs) and the decidability of their safety verification problems. It categorizes NNs based on their activation functions (e.g., piece-wise Noetherian, ReLU). For each category, it indicates which sections of the paper provide applicable results and whether the safety verification problem is decidable for that class of NNs, along with an example activation function.
In-depth insights#
Safe NN Control#
Safe NN control is a critical area of research because of the increasing use of neural networks in safety-critical systems. The core challenge lies in verifying the safety of neural network controllers (NNCSs), which is difficult due to the complexity of NNs and their interaction with physical systems. Current approaches often employ open-loop verification (analyzing NNs in isolation) which is insufficient to guarantee NNCS safety in real-world conditions, or closed-loop verification (analyzing NN and system together) limited to bounded time horizons and approximations. This paper introduces a novel approach, VerSAILLE, combining the rigor of differential dynamic logic (dL) with the efficiency of NN verification tools. This hybrid approach leverages existing control theory literature within dL to generate specifications, which are then verified using NN verification techniques. It presents Mosaic, an efficient method for verifying polynomial real arithmetic properties on piecewise linear NNs, overcoming the limitations of existing tools. VerSAILLE and Mosaic address the limitations of traditional approaches, enabling provably safe NN controllers with infinite-time safety guarantees.
VerSAILLE: NNCS#
VerSAILLE presents a novel approach to verifying the safety of Neural Network Control Systems (NNCSs). It leverages the rigor of differential dynamic logic (dL) to establish infinite-time safety guarantees, a significant improvement over existing time-bounded methods. The core innovation lies in its ability to bridge the gap between the symbolic reasoning of dL and the numerical nature of neural networks. VerSAILLE achieves this by using a proven dL control envelope as a specification, then verifying that a given NN adheres to this specification using existing NN verification tools. This process offers both soundness and completeness, ensuring that a verified NN’s behavior in the NNCS is provably safe for all time. The approach is further enhanced by Mosaic, a technique designed to handle the nonlinearities often encountered in NN verification. Mosaic efficiently and completely translates complex, nonlinear NN verification queries into simpler ones solvable by existing tools, resolving the inherent limitations of current NN verification technology.
Mosaic: NN Verify#
Mosaic: NN Verify likely presents a novel approach to verifying neural networks, particularly focusing on handling the complexities of nonlinear arithmetic and arbitrary logical structures within neural network control systems (NNCS). The core idea seems to revolve around partitioning complex verification queries into simpler, more manageable sub-queries, potentially utilizing off-the-shelf linear constraint tools for increased efficiency. This partitioning, analogous to a mosaic, allows for a more scalable and complete verification process compared to existing methods that struggle with nonlinearity. A key aspect may involve combining approximation techniques with exact reasoning to ensure both soundness and completeness, enabling a sound and complete verification of properties in polynomial real arithmetic on piecewise-linear NNs. The technique’s strength may lie in its ability to handle complex real-world scenarios where standard techniques are challenged by nonlinearities and logical structure. It likely demonstrates significant performance gains over existing approaches, as indicated by the name “Mosaic.” Completeness-preserving approximation combined with judicious SMT reasoning is likely key to overcoming the limitations of traditional NN verification.
N3V Tool: Results#
The hypothetical “N3V Tool: Results” section would present a comprehensive evaluation of the N3V tool’s performance on various benchmarks. The results would likely showcase VerSAILLE’s ability to prove infinite-time safety for several neural network-controlled systems (NNCS), a significant advancement over existing time-bounded methods. Mosaic’s efficiency and completeness in handling complex, nonlinear verification queries would also be highlighted, possibly including comparisons with other state-of-the-art tools to demonstrate superior performance. Specific case studies, such as adaptive cruise control and ACAS X, would be discussed in detail, showing how N3V successfully verified or identified unsafe regions within the NNCS. Furthermore, the results would address the scalability of N3V by presenting timing data and analyses across NN architectures of varying complexity, highlighting its applicability to real-world systems. The discussion would likely include details on the choice of approximation techniques employed by Mosaic, as well as any limitations or challenges encountered during the evaluation.
Future Work#
The authors outline several promising avenues for future research. They plan to extend N³V’s capabilities to handle a wider range of activation functions, beyond ReLU networks, enhancing its applicability. Improving the efficiency of the MOSAIC algorithm is another goal, aiming to reduce its computational cost for particularly complex systems. The team also intends to explore the application of MOSAIC in other contexts, such as neural barrier certificate verification, leveraging its efficiency and generality. Finally, they highlight the need for more comprehensive case studies, as the availability of infinite-time-safe NNCS benchmarks is currently limited, hindering a more complete assessment of VerSAILLE’s effectiveness and scalability. Addressing the challenge of NNCS safety across diverse and complex real-world scenarios represents a major focus for future research.
More visual insights#
More on figures
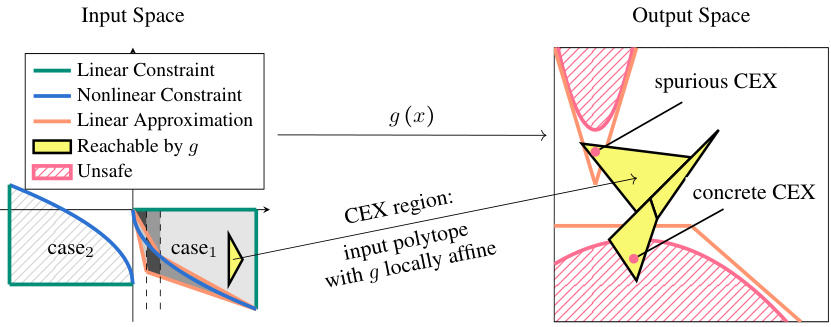
The figure visualizes how Mosaic, a nonlinear verification algorithm, handles nonlinear constraints in NN verification. It shows the input space partitioned into regions with linear approximations of nonlinear constraints. The NN’s behavior is analyzed in each region, considering reachable outputs. The output space highlights spurious and concrete counterexamples resulting from the linear approximations. This process aims for completeness and efficiency by combining approximation and SMT reasoning to verify complex properties on piecewise linear NNs.
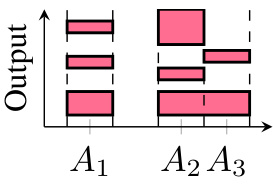
This figure illustrates the concept of Mosaic, a novel approach for handling nonlinear open-loop NNV queries. It shows how the input space is partitioned into regions (A1, A2, A3) which contain different linear and non-linear constraints. The algorithm efficiently addresses the arbitrary logical structure and polynomial constraints found in hybrid systems. Instead of processing all combinations of constraints individually, it partitions the problem into smaller subproblems (azulejos) making the verification process more efficient and practical for real-world applications.
The figure visualizes the nonlinear verification algorithm Mosaic. It shows how Mosaic handles nonlinear constraints in NN verification by combining approximation with exact reasoning. The input space is partitioned into regions where the NN is locally affine. Linear approximations of the constraints are generated, and these are used to check if unsafe regions are reachable. If a spurious counterexample is found, it is generalized to an affine region to preserve completeness. The algorithm combines off-the-shelf linear constraint tools with approximation and SMT reasoning to handle arbitrary logical structure in nonlinear constraints.
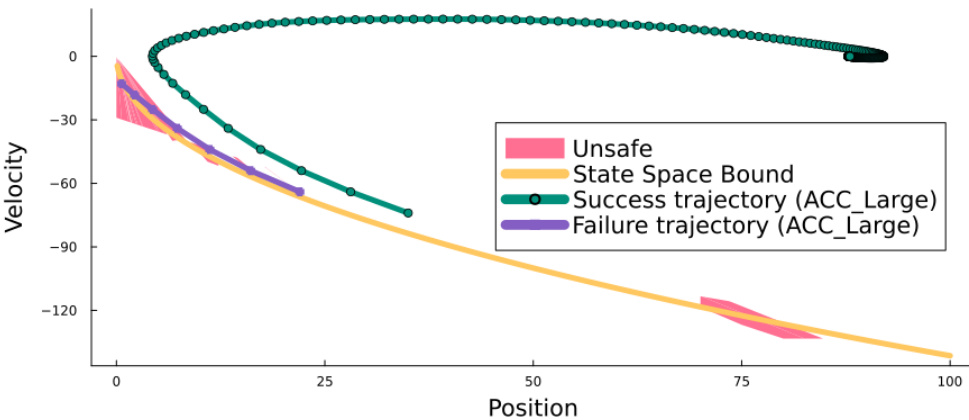
This figure shows the state space of the Adaptive Cruise Control (ACC) system with a large neural network (NN). The orange line demarcates the boundary of safe states. Red areas highlight regions where the NNCS exhibits unsafe behaviors (counterexamples). The green line illustrates a successful trajectory of the system, while the purple line shows an unsafe trajectory that leads to a collision. The dots along the trajectories represent individual control decisions.
The figure visualizes the nonlinear verification algorithm Mosaic. The left side shows the input space with linear and nonlinear constraints. The linear approximations are shown in orange lines. The blue and green areas represent two different input regions. The right side shows the output space with unsafe regions in red and reachable regions in green and blue. The algorithm aims to efficiently verify nonlinear properties by partitioning the input space and using off-the-shelf linear constraint tools for each partition.

The figure visualizes the nonlinear verification algorithm Mosaic. It shows how Mosaic handles nonlinear constraints in the verification of neural networks by combining approximation with exact reasoning. The input space is partitioned (creating a ‘mosaic’), and linear approximations are used for the nonlinear constraints. This allows lifting off-the-shelf linear constraint tools to the nonlinear setting while maintaining completeness. The figure illustrates how the algorithm identifies spurious counterexamples (spurious CEX) versus concrete counterexamples (concrete CEX) and how it partitions the input and output spaces for efficient verification.
The figure visualizes the process of the nonlinear verification algorithm Mosaic. The input space is shown on the left, where green and blue areas represent linear and nonlinear constraints, respectively. The algorithm partitions the input space into regions. Each region is analyzed for safety properties. The output space is shown on the right, where red areas indicate unsafe regions. The algorithm identifies concrete counterexamples and generalizes them to counterexample regions. This process combines approximation with exact reasoning to achieve completeness.
This figure visualizes the nonlinear verification algorithm Mosaic. The left side shows the input space with linear and nonlinear constraints. The nonlinear constraints are approximated by linear approximations (orange lines around the blue constraint). The input space is partitioned into regions (azulejos), each with its own open-loop NNV query. The right side shows the output space, highlighting spurious and concrete counterexamples. The algorithm determines whether the NN’s output reaches unsafe regions, effectively verifying nonlinear properties.
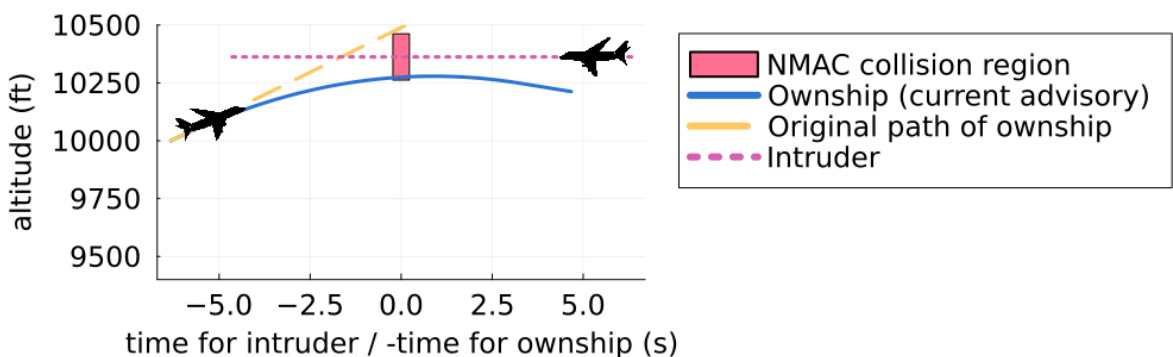
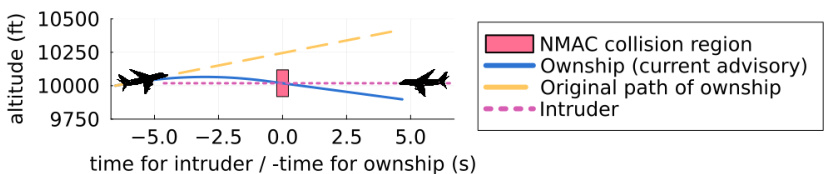
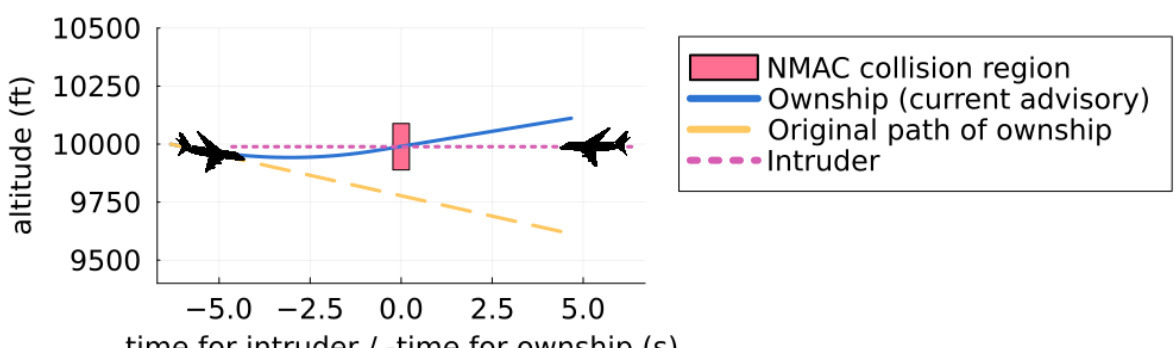
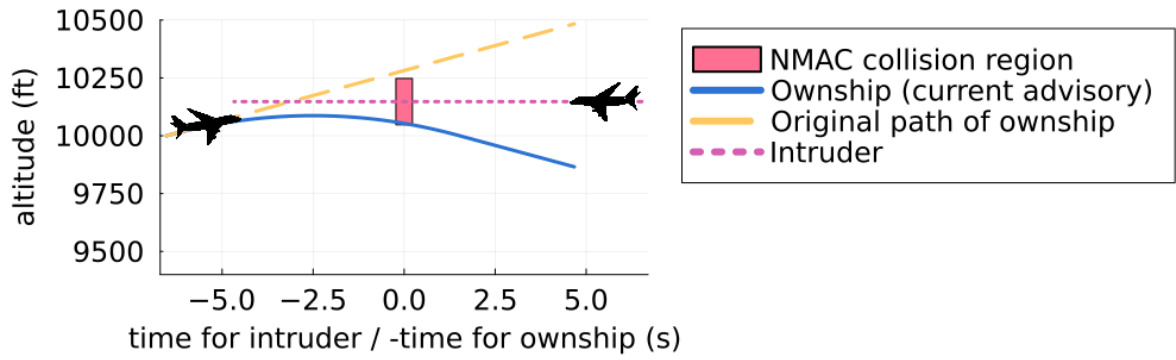
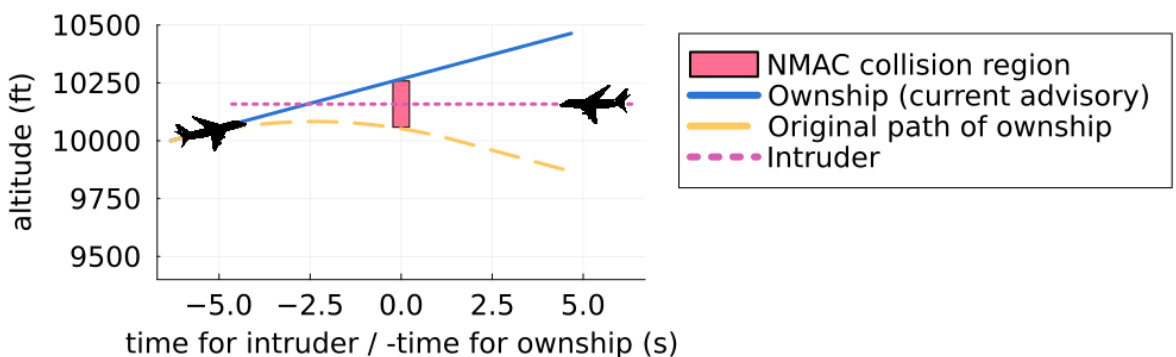
This figure shows a specific scenario where the Airborne Collision Avoidance Neural Network provides an unsafe advisory, leading to a near mid-air collision (NMAC). Initially advised to climb, the NN unexpectedly instructs a descent, resulting in a collision six seconds later. The figure highlights the trajectories of both aircraft, illustrating how the NN’s unsafe recommendation leads to a dangerous situation. Additional similar examples are detailed in Appendix G of the paper.
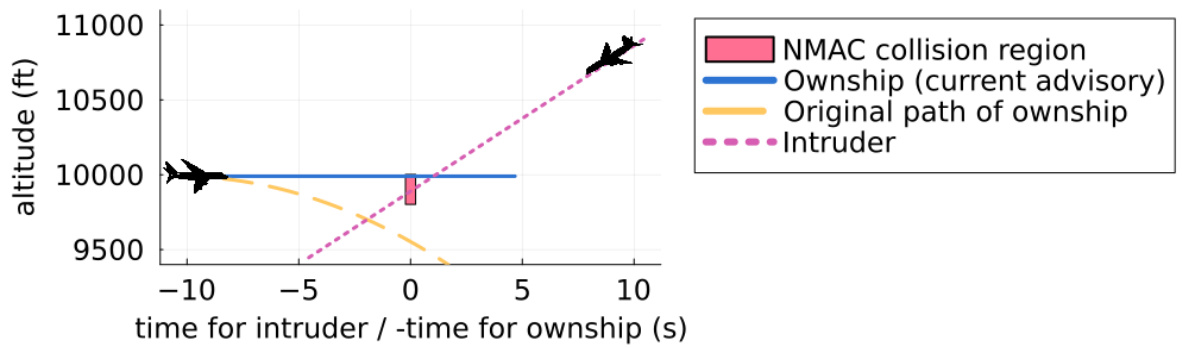
This figure shows an example of an unsafe advisory generated by the Airborne Collision Avoidance Neural Network. After receiving an advisory to climb, the NN subsequently advises a descent, leading to a near mid-air collision (NMAC) within 6 seconds. This highlights a failure case where the NN’s decision-making process resulted in an unsafe outcome, demonstrating the need for rigorous safety verification.
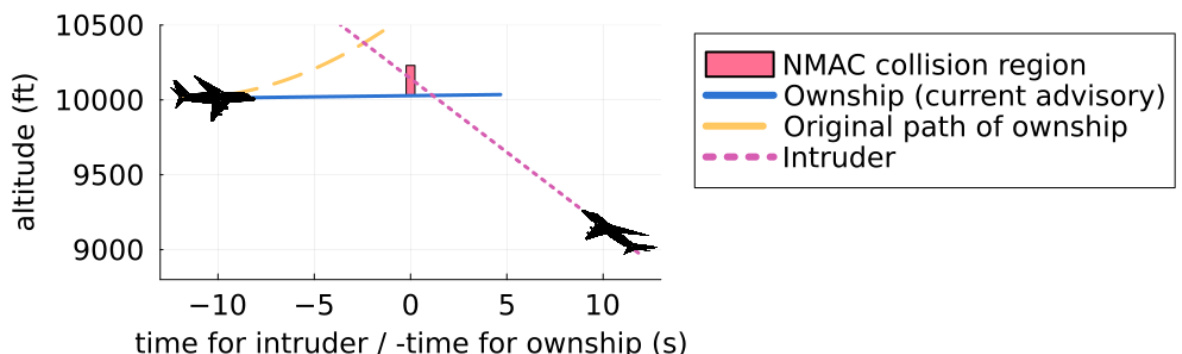
This figure shows an example of an unsafe advisory generated by the Airborne Collision Avoidance Neural Network. After initially advising a climb, the NN subsequently advises a descent, leading to a near mid-air collision (NMAC) within 6 seconds. This illustrates a failure case where the NN’s decision-making process results in an unsafe outcome, highlighting the importance of rigorous verification techniques.
More on tables

This table shows the applicability of the research results to different classes of neural networks (NNs). It demonstrates whether the proposed verification techniques can be applied to each NN class and if the safety verification problem is decidable for each NN class. The table is organized based on the complexity of the NN, ranging from piece-wise Noetherian to ReLU NNs. Each row specifies the type of activation function (all fᵢ, Noetherian, Polynomial, Linear), the type of constraints allowed (all qᵢ, FOLNR, FOLR, FOLLR), the sections of the paper where the results apply, whether the safety verification problem is decidable, and an example of an activation function for that class. The table shows that the methods are widely applicable but decidability is proven only for some.
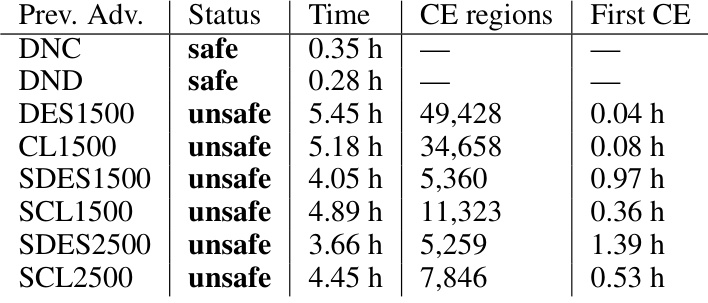
This table presents the results of verifying the safety of several neural networks used in the Airborne Collision Avoidance System (ACAS) for level flight scenarios. For each neural network, it shows the previous advisory given by the system, whether the system was deemed safe or unsafe by the verification process, the total runtime of the verification, the number of counterexample regions identified (indicating unsafe scenarios), and the time it took to find the first counterexample. The table demonstrates the effectiveness of the proposed verification approach in identifying and characterizing unsafe regions within the ACAS X system.
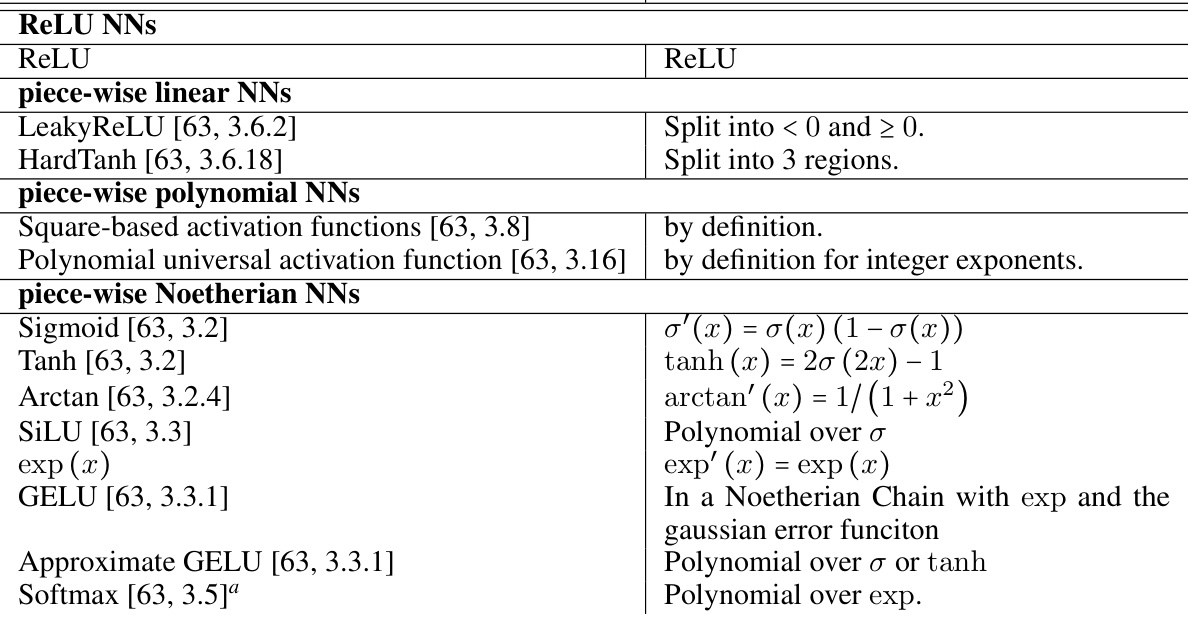
This table shows the applicability of the research results to different classes of neural networks (NNs) and indicates whether safety verification is decidable for each class. The NN classes are categorized based on the properties of their activation functions. The table indicates that the methods are applicable to all NNs with piecewise Noetherian activation functions, and that decidability is guaranteed for piecewise polynomial and piecewise linear NNs. A concrete example of each class and which sections of the paper they relate to is also included.

This table shows the applicability of the research results to different classes of neural networks and whether the safety verification problem is decidable for each class. The classes are hierarchical, with each class being a subset of the one above it. The table indicates whether the theoretical results and the implemented tool (N3V) can handle each class, and if the safety verification problem is decidable in each class.
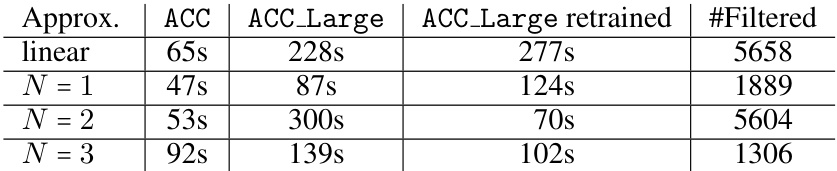
This table presents the runtimes of the N³V tool for verifying the safety of Adaptive Cruise Control (ACC) neural networks. It shows the performance for different neural network architectures (ACC, ACC_Large, and a retrained version of ACC_Large) using various approximation levels (linear, N=1, N=2, N=3). The ‘#Filtered’ column indicates the number of spurious counterexamples that were filtered out by the tool during the verification process. The runtimes are in seconds.
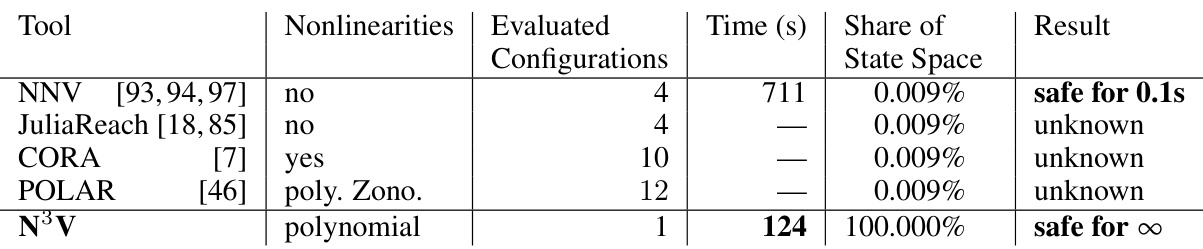
This table compares the performance of various verification tools on the Adaptive Cruise Control (ACC) benchmark. It contrasts tools’ abilities to handle nonlinearities, the number of configurations tested, the runtime, the proportion of the state space explored, and the verification result (whether safety was proved for a short time or infinitely). N³V, the authors’ tool, significantly outperforms others, achieving full state-space verification for infinite time.
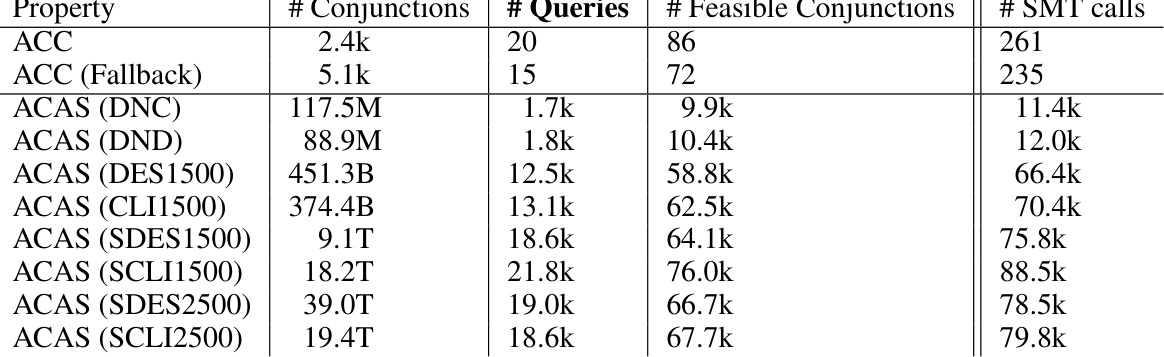
This table compares the number of queries generated by different methods for verifying non-normalized open-loop neural network verification (NNV) queries. It shows that the MOSAIC approach significantly reduces the number of queries compared to other methods, leading to improved efficiency. The table includes the number of propositionally satisfiable conjunctions, the number of open-loop NNV queries, the number of queries when splitting disjunctions, and the number of SMT calls for each method. This highlights the benefits of the MOSAIC approach in terms of computational cost.
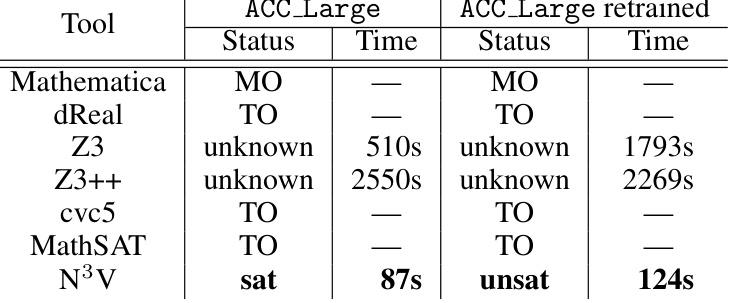
This table compares the performance of N³V against other state-of-the-art SMT solvers (dReal, Z3, Z3++, CVC5, MathSAT) on two different neural networks: ACC_Large and a retrained version of ACC_Large. The comparison focuses on the time taken to verify or refute the safety properties (represented as ‘sat’ for satisfiable/safe and ‘unsat’ for unsatisfiable/unsafe). It demonstrates N³V’s efficiency compared to other SMT solvers, especially for complex safety verification tasks, showing it is able to achieve results within 124 seconds that other tools failed to achieve in 12 hours.

This table lists the allowed advisories for a Vertical Airborne Collision Avoidance System. For each advisory, it provides a description, the allowed range of vertical velocity (in ft/min), and the minimum required acceleration (g/x where x is a numerical value).
Full paper#



















