Inexact Augmented Lagrangian Methods for Conic Optimization: Quadratic Growth and Linear Convergence

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it resolves a long-standing open question regarding the asymptotic linear convergence of primal iterates in Augmented Lagrangian Methods (ALMs) for semidefinite programs (SDPs). It provides new theoretical guarantees for ALM performance, impacting various applications. This opens avenues for improved algorithm design and a deeper understanding of ALM convergence behavior. The symmetric versions of inexact ALMs introduced here are also a significant contribution.

Visual Insights

#

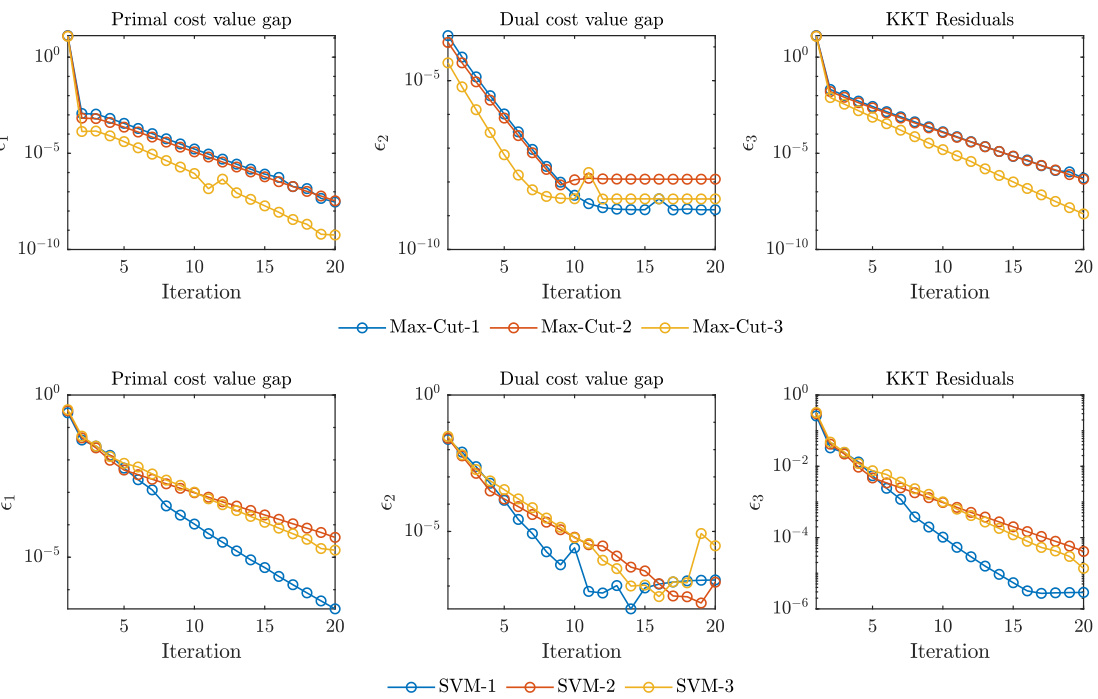
This figure displays the convergence behavior of the inexact Augmented Lagrangian Method (ALM) applied to Max-Cut and linear SVM problems. Three different instances of each problem are shown. The plots illustrate the convergence of the primal cost value gap, dual cost value gap, and KKT residuals. The symbol ε represents the maximum of five different KKT residuals, indicating the overall convergence of the algorithm toward optimality. The results demonstrate the linear convergence of the algorithm, as evidenced by the roughly linear decrease in the plotted values on a logarithmic scale.

In-depth insights

#

SDP Growth Analysis

#

An SDP growth analysis in the context of optimization algorithms investigates how the objective function of a semidefinite program (SDP) behaves near its optimal solution. Quadratic growth is a key property often studied, showing that the objective function increases at least quadratically with the distance from the optimum. Establishing quadratic growth is crucial because it implies linear convergence rates for many iterative algorithms used to solve SDPs, such as augmented Lagrangian methods (ALMs). An analysis might explore different conditions under which quadratic growth holds, including strict complementarity, which ensures the existence of unique primal and dual solutions. The analysis may also consider the impact of problem structure, constraints, and regularization techniques on growth properties. Furthermore, a rigorous analysis would compare and contrast various SDP growth results found in the literature, highlighting differences in assumptions and techniques, and ultimately clarifying the implications for the performance of specific algorithms. Error bounds, which quantify the distance to the optimal solution set in terms of the suboptimality or constraint violation, are closely related to growth conditions and may be a key aspect of such an analysis. The ultimate goal is to provide stronger theoretical underpinnings for algorithms used in solving SDPs, which have broad applications in various fields, such as control theory, machine learning, and combinatorial optimization.

Inexact ALM

#

Inexact Augmented Lagrangian Methods (ALMs) address the computational challenges of solving large-scale optimization problems by relaxing the requirement for exact minimization in each iteration. This inexactness is crucial for scalability, as it allows the use of efficient approximate solvers. The paper analyzes the convergence properties of these inexact ALMs, demonstrating linear convergence for both primal and dual iterates under the assumption of strict complementarity. This result is significant because it provides theoretical guarantees for the impressive empirical performance observed in practice. The authors also explore the nuances of using inexact ALMs, clarifying the role of the penalty parameter and establishing symmetric versions for both primal and dual SDPs. Establishing quadratic growth and error bound properties for primal and dual SDPs is key to proving linear convergence, demonstrating a deeper understanding of the underlying problem structure. The work’s contribution extends beyond mere algorithmic improvements; it provides a deeper theoretical understanding, directly impacting the design and implementation of effective solvers for SDPs and related problems.

Primal Convergence

#

The concept of ‘Primal Convergence’ in the context of optimization algorithms, particularly Augmented Lagrangian Methods (ALMs), focuses on how quickly the sequence of primal iterates approaches an optimal solution. Unlike dual convergence, which often enjoys readily available linear convergence guarantees under standard assumptions, establishing primal convergence rates has been a significant challenge. This is because ALMs are fundamentally dual-based methods where the primal iterates are derived indirectly. The paper addresses this gap by showing that under strict complementarity and a bounded solution set, the primal iterates of ALMs applied to semidefinite programs converge linearly. This result is crucial because it establishes a symmetric convergence property, mirroring the well-known dual convergence behavior. The novelty lies in proving quadratic growth and error bound properties for both the primal and dual problems, which are key to establishing linear convergence. These properties are crucial for characterizing the behavior of ALMs in high-dimensional spaces. The authors offer a new perspective on exact penalty functions, leading to a simplified and more elegant proof of the convergence results.

Strict Complementarity

#

Strict complementarity is a crucial concept in optimization, particularly within the context of conic programming. It essentially describes a relationship between primal and dual optimal solutions, suggesting that at optimality, the slackness in either the primal or dual problem should be zero. This condition, often assumed for theoretical analysis, significantly impacts the convergence properties of algorithms, such as augmented Lagrangian methods (ALMs), ensuring that iterates reach optimality efficiently. The paper highlights the importance of this condition by demonstrating that linear convergence of both primal and dual iterates in ALMs hinges upon strict complementarity. This is a key finding as it resolves an open question on the convergence rate of primal iterates. However, the assumption of strict complementarity is not always satisfied in practical applications; thus, the paper’s implications are most impactful when the condition is met. Further research should focus on the implications when this condition is relaxed and explore alternative techniques for handling scenarios lacking strict complementarity.

Future Directions

#

Future research could explore relaxing the strict complementarity assumption, which, while common, might limit applicability. Investigating the impact of different penalty parameter choices and inexactness criteria on convergence rates would refine the algorithm’s practical use. Extending the theoretical analysis to handle more general conic programs beyond SDPs is vital. Furthermore, empirical studies on larger-scale problems, especially those arising in machine learning and polynomial optimization, would strengthen the findings. Finally, the development of efficient numerical methods to solve the subproblems within the ALM framework could be beneficial, enhancing overall performance. Exploring the potential for parallelization within the ALM framework is also a promising avenue to unlock scalability.

More visual insights

#

More on figures

This figure shows that even a simple 2x2 SDP does not have sharp growth. It illustrates the quadratic growth property of the exact penalty function f(y) = −bTy + p max{0, λmax(A*(y) − C)} with p = 4 and optimal solution at (0,0). The 3D view shows regions where the linear term dominates (yellow), both linear and non-linear components are active (blue), and the quadratic growth (green) is apparent. The sectional view illustrates the non-linearity of the function.

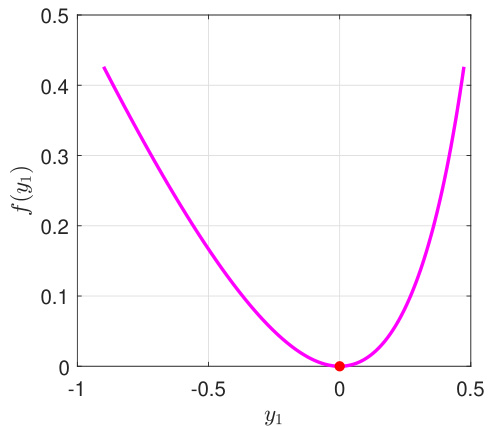
This figure shows the quadratic growth property of the exact penalty function f(y) = −by+pmax{0, Amax(A*(y)−C’)}. The 3D plot shows the function’s landscape, highlighting regions where the linear and non-linear components dominate. The 2D plot is a cross-section illustrating the quadratic growth near the optimal solution.

The figure shows the convergence behavior of the inexact ALM (15) for Max-Cut and linear SVM problems. Three instances are tested for each problem. For each instance and problem, three curves are plotted, showing the convergence of the primal cost value gap (the difference between the current primal cost and the optimal cost), the dual cost value gap (the difference between the current dual cost and the optimal cost), and the KKT residuals (the maximum of several measures indicating the optimality gap). The results demonstrate linear convergence of the ALM for all tested instances, indicating that both primal and dual iterates converge linearly to the optimal solution.

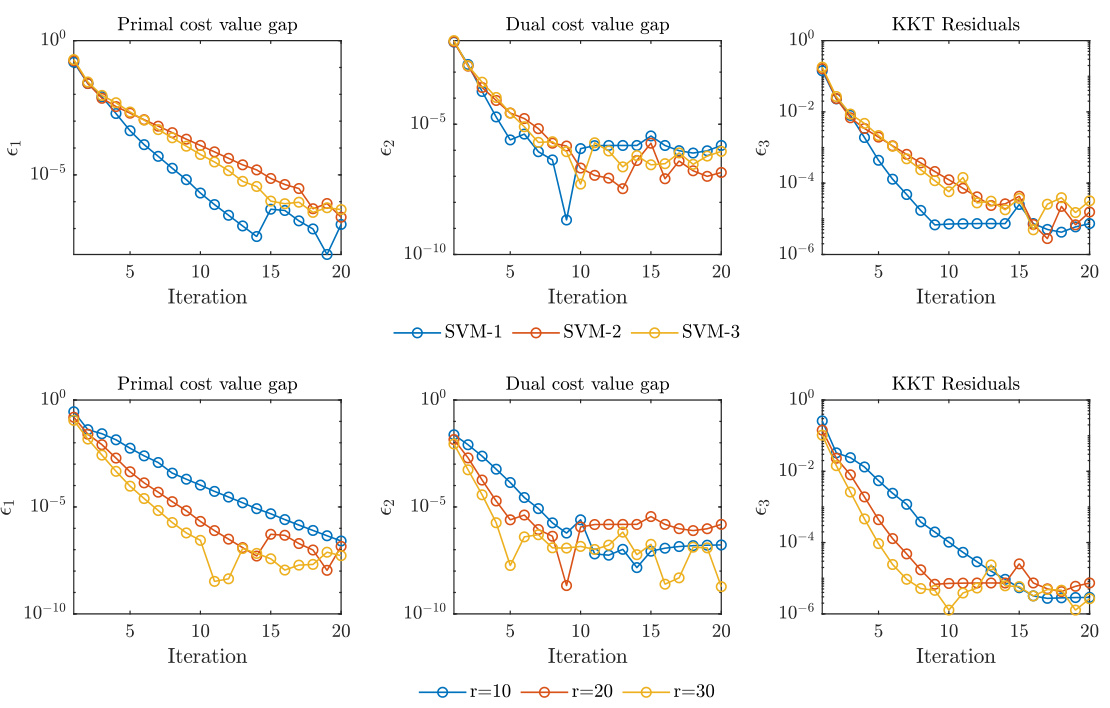
The figure shows the numerical convergence behavior of the inexact ALM (15) for Max-Cut and linear SVM problems. It displays the primal cost value gap, dual cost value gap, and KKT residuals over iterations for three different instances of each problem (Max-Cut 1-3, SVM 1-3). The KKT residuals are represented by epsilon3, which is the maximum of five different residuals (71-75). The plots illustrate the linear convergence of both primal and dual iterates towards optimality, as indicated by the decreasing gaps and residuals over the iterations.

This figure displays the convergence behavior of the inexact ALM (15) algorithm applied to Max-Cut and linear SVM problems. It shows the convergence of the primal cost value gap, the dual cost value gap, and the KKT residuals for three different instances of each problem. The plots illustrate the algorithm’s linear convergence, as indicated by the decreasing error over iterations. The KKT residuals (€3) represent the maximum of five error metrics measuring the closeness to optimality. The consistent decrease across the metrics suggests the efficiency of the inexact ALM approach in solving both Max-Cut and linear SVM problems.

Full paper

#