Optimal Hypothesis Selection in (Almost) Linear Time

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in hypothesis selection and density estimation. It presents the first almost linear-time algorithm achieving optimal accuracy, a long-standing open problem. This breakthrough impacts various fields, enabling efficient model selection and improved learning algorithms for structured distributions, and opens new avenues for research in sublinear-time hypothesis selection.

Visual Insights

#

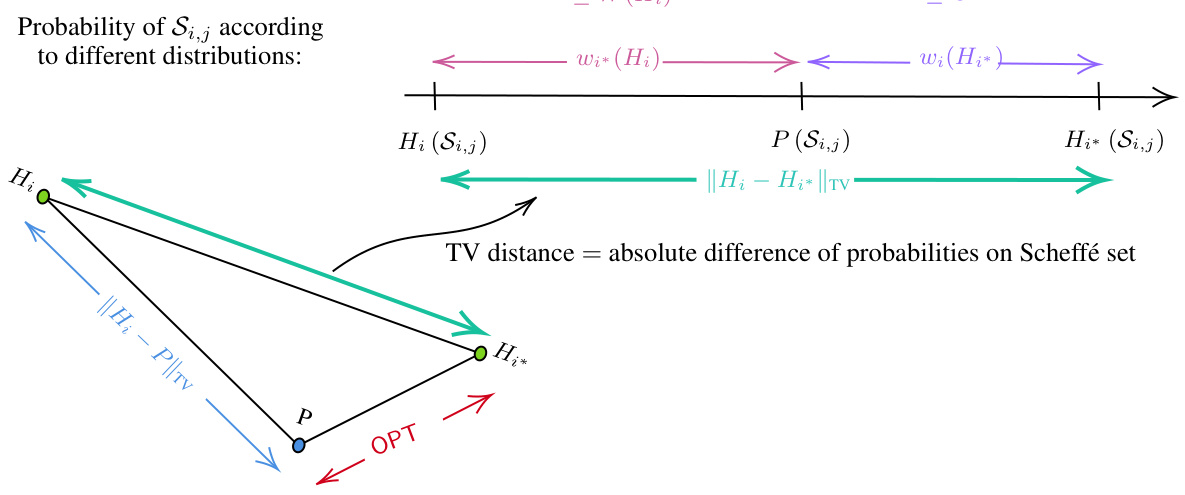
This figure illustrates how the total variation distance ||H₁ – P||tv between a hypothesis H₁ and the true distribution P can be bounded using the semi-distance wᵢ*(Hᵢ) and OPT (the distance between P and the closest hypothesis Hᵢ* in H). The triangle inequality shows that ||H₁ – P||tv ≤ ||H₁ – Hᵢ*||tv + ||Hᵢ* – P||tv. The semi-distance wᵢ*(Hᵢ) is defined as |Hᵢ(Sᵢ,ⱼ) - P(Sᵢ,ⱼ)|, where Sᵢ,ⱼ is the Scheffé set for Hᵢ and Hᵢ*. The figure demonstrates that wᵢ*(Hᵢ) is a lower bound for ||Hᵢ – P||tv, and W(Hᵢ) (the maximum semi-distance for Hᵢ) is used as a proxy for the quality of Hᵢ because it is an upper bound for wᵢ*(Hᵢ).

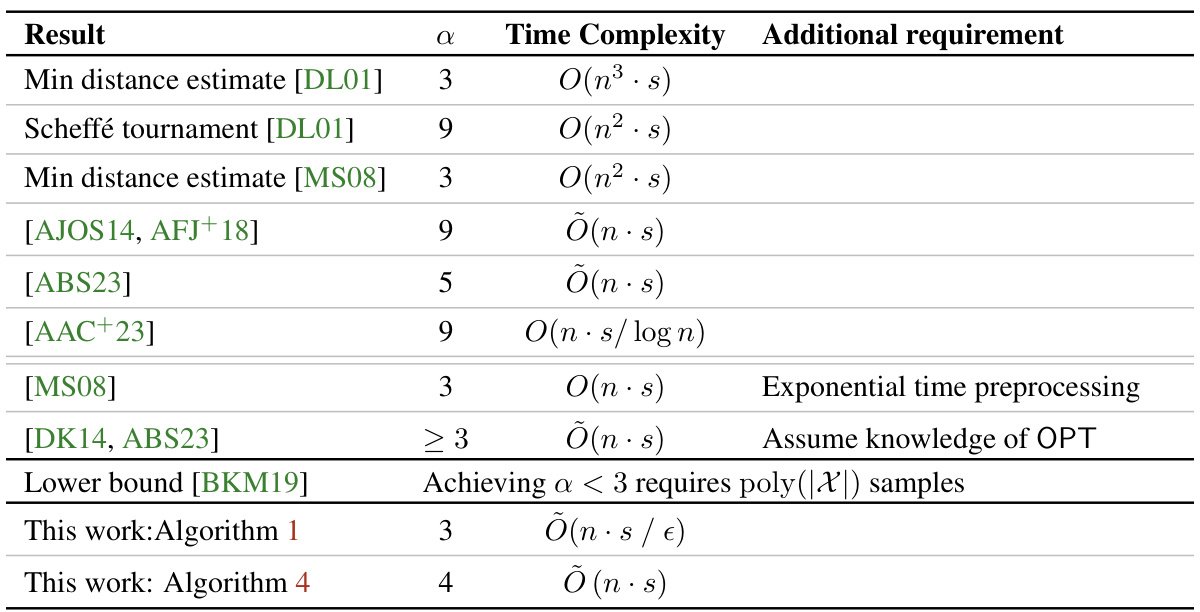
The table summarizes the time and sample complexities, and the accuracy parameter (alpha) of various hypothesis selection algorithms from prior works. It highlights the trade-off between achieving a smaller alpha (optimal accuracy) and the computational efficiency of the algorithms. The table shows that previous algorithms either had worse time complexities, larger alpha factors, or required additional assumptions.

In-depth insights

#

Optimal a=3 Achieved

#

The claim of “Optimal a=3 Achieved” in a hypothesis selection algorithm is a significant breakthrough, suggesting the algorithm achieves the best possible multiplicative constant (a) relating the algorithm’s error to the optimal error achievable with a given hypothesis class. Achieving a=3 is optimal in the minimax sense, meaning no other algorithm can guarantee a smaller constant factor in the error bound. This optimality is particularly noteworthy considering that previous algorithms could only achieve a>3, requiring significantly more computational resources or additional assumptions about the underlying distribution. The paper likely demonstrates this optimality result through rigorous theoretical analysis and provides a detailed algorithm achieving this bound. However, it is important to note that the claim of optimality may be limited to a specific setting, such as a particular class of distributions or access model. The runtime complexity of the algorithm is also critical; an optimal a=3 result is less impactful if the algorithm requires computationally prohibitive resources. Therefore, a complete evaluation would also need to consider the algorithm’s efficiency (e.g., runtime, memory usage) in relation to the optimality of the a=3 factor. The practical implications of this optimal a=3 result in various applications of hypothesis selection could then be discussed. Overall, “Optimal a=3 Achieved” represents a substantial advance in the field, but needs further context to fully assess its significance.

Near-Linear Time Algo

#

The heading ‘Near-Linear Time Algo’ likely refers to a section detailing algorithms achieving near-linear time complexity. This is a significant improvement in the field of hypothesis selection, as previous optimal algorithms had quadratic or cubic time complexities. Near-linear time (Õ(n)) means the algorithm’s runtime grows proportionally to the input size (n), up to logarithmic factors, enabling efficient processing of large datasets. The paper likely showcases novel techniques to reduce the computational burden, possibly involving clever data structures, approximation schemes, or randomized algorithms. Achieving near-linear time while maintaining optimal accuracy (e.g., a factor of 3) is a major theoretical breakthrough, addressing a long-standing open problem. The discussion likely contrasts this achievement with previous work, highlighting the efficiency gains while ensuring the accuracy guarantees remain strong. The details likely involve analysis of the algorithm’s time complexity, including a breakdown of the dominant steps and a rigorous proof of its near-linear bound. The practical implications are substantial: this improved efficiency makes hypothesis selection feasible for significantly larger datasets or real-world applications where computation time is a limiting factor.

Hypothesis Selection

#

Hypothesis selection, a crucial problem in statistics and machine learning, focuses on choosing the best-fitting distribution from a set of candidate distributions (hypotheses) to represent an unknown data-generating process. The paper highlights the challenge of balancing accuracy and computational efficiency, with a core focus on the approximation factor (alpha) that dictates how close the selected hypothesis is to the true distribution. Existing algorithms often struggled with either high alpha values, leading to less accurate estimations, or high computational complexity, making them impractical for large datasets. This research presents novel algorithms that achieve near-optimal linear time complexity (almost linear in the number of samples) while maintaining a small, near-optimal alpha. The algorithms employ innovative techniques to reduce computation time, leveraging semi-distance estimates and carefully designed update strategies for hypotheses. A particularly valuable aspect is the algorithms’ ability to achieve the optimal accuracy parameter (alpha=3) in almost linear time, improving upon prior work that either had higher alpha values or required significantly more computational resources. The improved efficiency allows the application of hypothesis selection to much larger datasets and complex modeling problems than before. The paper further explores algorithms with trade-offs between computational cost and accuracy, offering choices to suit different needs.

Improved Accuracy

#

The concept of “Improved Accuracy” in a PDF research paper would likely involve a discussion of methods to enhance the precision and reliability of results. This could encompass several strategies. Algorithmic advancements might be a central theme, detailing modifications to existing algorithms or the introduction of novel techniques to reduce error rates. Data preprocessing methods might also be discussed, exploring ways to improve the quality and consistency of the data used for analysis. This often includes techniques like handling missing values, outlier detection, and noise reduction. Model selection and evaluation would likely feature prominently, illustrating the careful selection of appropriate models and rigorous validation methods (like cross-validation or bootstrapping) to ensure that reported results are generalizable and not simply due to chance. Parameter tuning would be another aspect, describing how optimal parameter settings for the algorithms or models were determined and the impact of these choices on overall accuracy. Finally, the paper would likely include a detailed quantitative analysis comparing improved results with prior work, and possibly include a discussion on the trade-offs between accuracy and other factors such as computational complexity or interpretability.

Future Research

#

The paper’s significant advancement in hypothesis selection using almost linear time algorithms opens exciting avenues for future research. A primary direction involves bridging the remaining gap to achieve truly linear time complexity while maintaining optimal accuracy (a=3). This requires deeper investigation into algorithmic techniques that can eliminate the currently existing polylogarithmic factors. Another key area is improving the dependency on the accuracy parameter (ε). While the paper presents algorithms with improved dependencies, further optimizations can lead to more efficient algorithms especially in low-ε settings. Furthermore, extending the algorithm to handle improper learning scenarios would be highly valuable, allowing the algorithm to select a hypothesis that isn’t necessarily part of the predefined set. Finally, exploring real-world applications to showcase the practical benefits of this efficient hypothesis selection approach and validating performance in varied scenarios is crucial. This includes exploring the algorithm’s robustness when handling noisy data and datasets with intricate characteristics. Research in these directions would contribute to both theoretical understanding and impactful practical applications of hypothesis selection.

More visual insights

#

More on tables

This table summarizes the time and sample complexities, and accuracy parameter (alpha) of various hypothesis selection algorithms from prior works. It highlights the trade-off between achieving a smaller alpha (optimal accuracy) and computational efficiency. The table also notes additional requirements some algorithms may have, such as preprocessing or knowledge of OPT.

This table summarizes previous research on hypothesis selection, focusing on the trade-off between the accuracy parameter (α) and time complexity. It shows that achieving a near-optimal accuracy parameter (α=3) typically came at the cost of high time complexity (O(n³s) or O(n²s)). The table highlights the improvement achieved by the authors’ work, which achieves α=3 with almost linear time complexity.

This table summarizes previous research on hypothesis selection, focusing on the trade-off between the accuracy parameter (α) and time complexity. It shows the different algorithms, their achieved α values, time complexities, and any additional requirements. The table highlights the improvement achieved by the authors’ work, which achieves near-linear time complexity with an optimal accuracy parameter. All algorithms listed use an optimal sample complexity of O(log n/ε²).

This table summarizes the time and sample complexities, and the accuracy parameter (alpha) of several previously published hypothesis selection algorithms. It highlights the trade-off between accuracy and computational efficiency, showing how different algorithms achieve various levels of accuracy (represented by alpha) with varying time complexities. The table also notes any additional requirements or assumptions made by each algorithm, such as knowledge of OPT or exponential preprocessing time. It helps to contextualize the contributions of the current paper by demonstrating the improvements it achieves in terms of time complexity and accuracy compared to existing approaches.

Full paper

#