The Intelligible and Effective Graph Neural Additive Network

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on graph neural networks and interpretable machine learning. It directly addresses the critical need for transparency in AI applications, particularly in high-stakes domains. The proposed method, GNAN, offers a novel approach that combines high accuracy with full model interpretability, paving the way for trustworthy AI solutions and opening up new avenues of research in both fields. This work challenges the common trade-off between accuracy and interpretability in machine learning models and provides a practical and effective solution for creating reliable and trustworthy AI systems. The interpretable nature of the model allows for a deeper understanding of decision-making processes, enhancing the model’s reliability and enabling easier debugging and bias detection.

Visual Insights

#

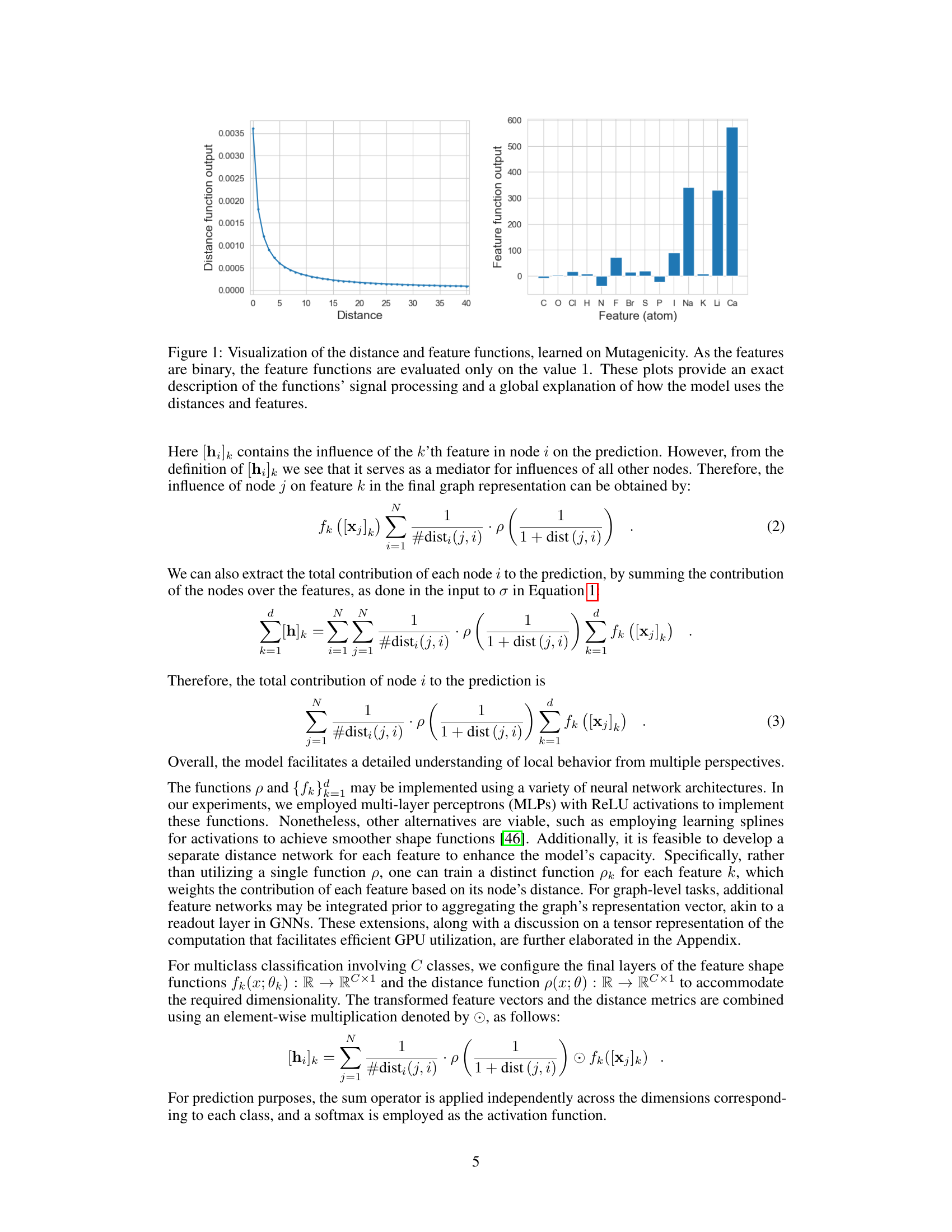
This figure visualizes the learned distance and feature functions of a GNAN model trained on the Mutagenicity dataset. The left panel shows the distance function, illustrating how the model weighs the influence of nodes based on their distance from a given node. The right panel displays the feature functions for each atom type, indicating their individual contribution to the model’s predictions. Because the features are binary (0 or 1), the feature functions are only shown for the value 1. Together, these plots provide a complete and interpretable representation of the model’s inner workings.

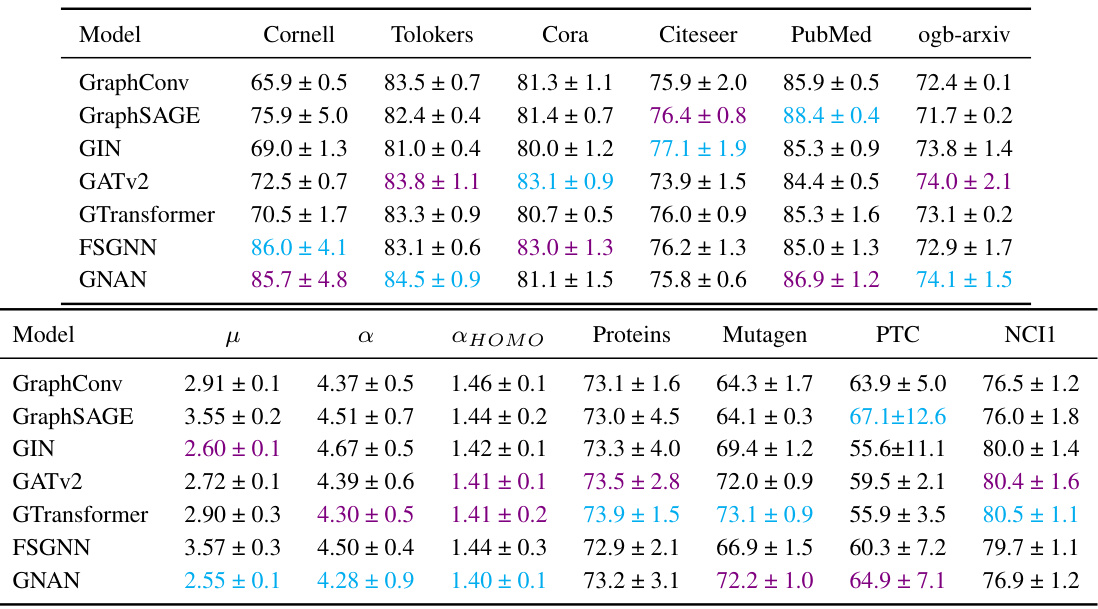
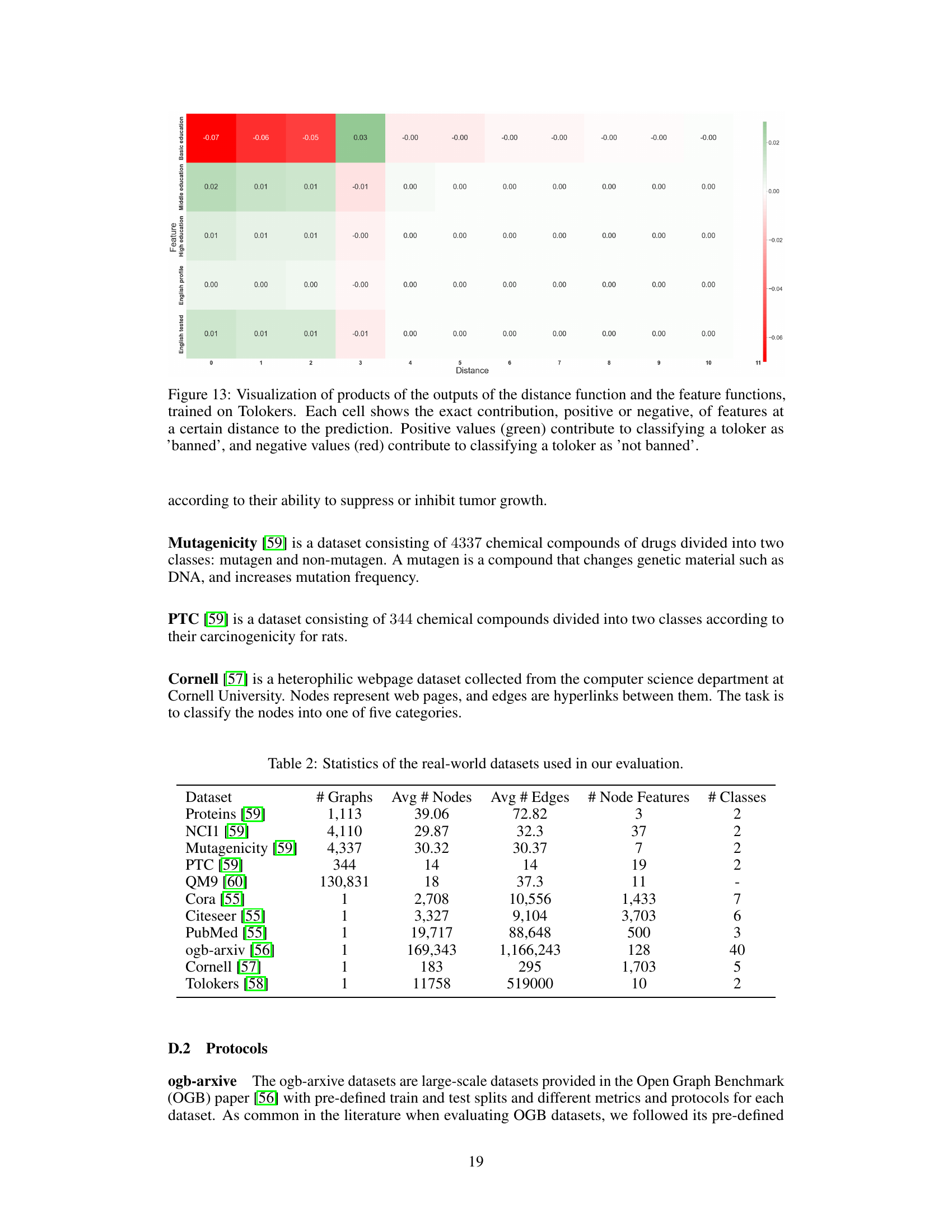
This table presents the results of experiments comparing the performance of Graph Neural Additive Networks (GNAN) with several other Graph Neural Network (GNN) models on various node and graph classification and regression tasks. The performance is measured by accuracy (with standard deviation) for most datasets and ROC-AUC (with standard deviation) for the Tolokers dataset and MAE (with standard deviation) for the μ, α, and ΔHOMO datasets. The best and second-best performing models for each task are highlighted.

In-depth insights

#

Interpretable GNNs

#

Interpretable Graph Neural Networks (GNNs) aim to address the black-box nature of many GNNs, which hinders their use in high-stakes applications demanding transparency. Explainability and interpretability are crucial for understanding model decisions, identifying biases, and ensuring trustworthiness. While many post-hoc methods exist to explain black-box GNNs, building interpretable GNNs by design offers a more robust solution. This involves designing the model’s architecture and learning processes to be inherently transparent, allowing for direct insight into how the model makes predictions. This might involve using simpler model architectures like additive models, or incorporating mechanisms for visualizing the model’s internal representations and feature importance. The challenge lies in balancing interpretability with accuracy, as simpler models may sacrifice predictive power. Research in interpretable GNNs is actively exploring various approaches to achieve this balance, leading to more trustworthy and understandable AI solutions.

GAMs for Graphs

#

Extending Generalized Additive Models (GAMs) to graph data presents a compelling avenue for creating interpretable graph neural networks (GNNs). GAMs’ inherent interpretability, stemming from their additive nature and the use of univariate functions for each feature, is highly attractive for applications demanding transparency. A key challenge lies in adapting the additive structure of GAMs to the complex relational nature of graph data. The approach might involve decomposing the graph into local substructures or features and applying GAMs to each, or by modeling the interactions of node features in an additive way using distance-based kernels. Visualizing the learned univariate functions is crucial to maintain the model’s interpretability. This allows for analyzing feature contributions and identifying interactions directly from the model, which would be a significant step beyond current black-box GNN explanations. Successful implementation would deliver a GNN that balances predictive power with the ease of understanding, making it suitable for critical decision-making scenarios requiring transparency and high accuracy.

GNAN Visualizations

#

GNAN visualizations are crucial for understanding the model’s inner workings. They offer a unique level of interpretability by directly showcasing the learned functions (distance and feature shape functions). The visualizations provide both global and local explanations, allowing users to grasp the overall model behavior and pinpoint specific feature contributions. Global interpretability is achieved through plots of these functions, offering a complete picture of the model’s logic. This contrasts sharply with typical black-box GNNs, where such insights are often unavailable. Local explanations further illuminate how specific nodes and features impact predictions for individual instances. The visualizations, therefore, are not merely supplementary, but rather fundamental to the GNAN approach. They enable model debugging, bias detection, and a deeper understanding of the model’s decision-making process, making GNAN particularly useful in high-stakes applications where transparency is paramount.

GNAN Performance

#

GNAN’s performance is a key aspect of the research paper. The authors benchmark GNAN against several state-of-the-art black-box GNNs across various graph and node labeling tasks. GNAN demonstrates competitive performance, often achieving results comparable to, or even surpassing, more complex models. This is particularly noteworthy because GNAN prioritizes interpretability, often a trade-off with accuracy in machine learning models. The strong empirical results suggest that high accuracy and strong interpretability are not mutually exclusive. The authors highlight GNAN’s superior performance on long-range tasks, showcasing its ability to capture relationships between distant nodes in a graph, a challenge for many other GNNs. Further analysis reveals that GNAN’s performance is consistent across different datasets and tasks. This robustness underscores its potential for use in diverse critical applications where both accuracy and transparency are paramount. Overall, the performance evaluation provides compelling evidence for GNAN’s effectiveness and its potential to be a valuable tool in fields requiring trustworthy AI.

Future Extensions

#

Future extensions of Graph Neural Additive Networks (GNAN) could significantly enhance its capabilities and impact. Improving the smoothness of learned shape functions through techniques like splines or adaptive activation functions is crucial for enhanced interpretability and potentially better performance. Exploring more sophisticated distance functions beyond simple shortest paths, such as those incorporating weighted edges or higher-order graph structures, could lead to improved model accuracy and better capture of complex graph relationships. Investigating different aggregation methods beyond the simple summation used currently in GNAN, such as attention mechanisms, would improve expressivity. Additionally, applying GNAN to diverse graph tasks, including link prediction and graph classification, and evaluating it on different types of graph datasets, are necessary. Finally, exploring efficient GNAN implementation, potentially leveraging hardware acceleration, is needed for scalability and applicability to large graphs. Addressing challenges posed by heterophily in graph data and the incorporation of temporal dynamics into the GNAN architecture are essential future directions.

More visual insights

#

More on figures

This figure visualizes the distance and feature functions learned by the GNAN model on the Mutagenicity dataset. The left panel shows the distance function (p), illustrating how the distance between atoms influences the model’s prediction. Since the features are binary (0 or 1), the right panel displays the feature functions (fk) only for the value 1, showing the impact of each atom type on the mutagenicity prediction. The plots together provide a complete, global view of how the model integrates distance and feature information for predictions.

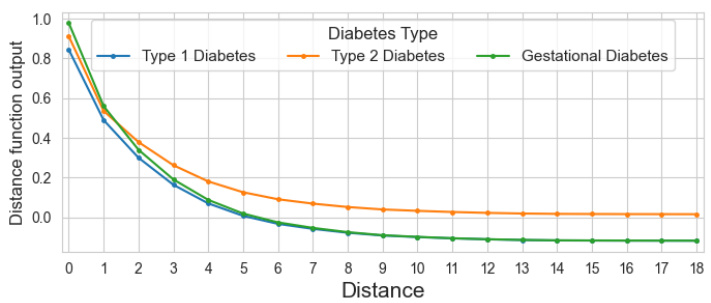
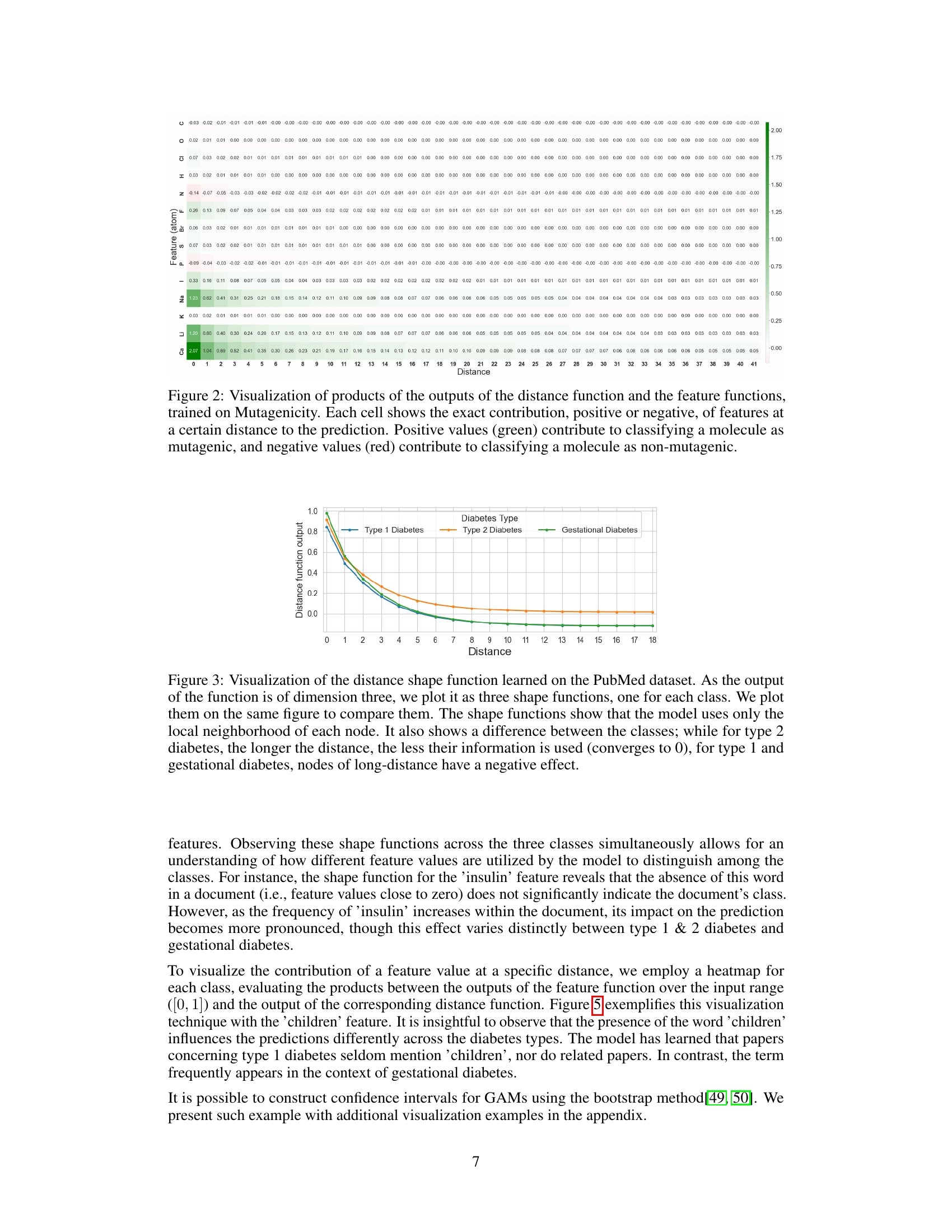
This figure visualizes the distance shape function learned by the GNAN model on the PubMed dataset. Because the model predicts three classes (Type 1, Type 2, and Gestational diabetes), three separate functions are shown, one for each class. The plot reveals that the model primarily uses information from nodes within a short distance; the influence decreases as the distance increases. A key observation is the difference in how distance affects the three classes: for Type 2 diabetes, the effect diminishes to almost zero at longer distances, while for Type 1 and Gestational diabetes, more distant nodes have a negative influence.

The figure visualizes the learned distance and feature functions of a GNAN model trained on the Mutagenicity dataset. The left panel shows the distance function, illustrating how the model weights the influence of nodes based on their distance from a given node. The right panel displays the feature functions, showing the relationship between each atom type (feature) and the model’s prediction. Because features are binary, only the function output for the value ‘1’ is shown. Together, these plots offer a complete, visual explanation of the model’s behavior, demonstrating the global interpretability of GNAN.

This figure visualizes the distance shape functions learned by the GNAN model on the PubMed dataset for the three different diabetes types. It shows how the model weighs the importance of information from different distances of nodes. The plots reveal that the model primarily utilizes information from nearby nodes and that the influence of distant nodes diminishes, especially for type 2 diabetes. Type 1 and gestational diabetes show a different pattern, where distant nodes have a negative influence.

This figure provides local explanations for two molecules from the Mutagenicity dataset. Each molecule is represented as a graph where nodes are atoms and edges are bonds. The size of each node is proportional to its importance in the model’s prediction, calculated using Equation 3. The figure highlights the crucial substructures contributing to the model’s classification of each molecule as mutagenic. In (a), a carbon ring is highlighted, and in (b), a NO2 subgraph is highlighted, showcasing known mutagenic features. These visualizations demonstrate GNAN’s ability to provide easily interpretable local explanations, aligning with prior biological knowledge.

The figure visualizes the learned distance and feature functions of a GNAN model trained on the Mutagenicity dataset. The left plot shows the distance function (p), illustrating how the model weighs the influence of nodes based on their distance from a target node. The right plot displays the feature functions (fk), demonstrating the relationship between each feature and the target variable. The visualizations offer a global interpretation of the model’s inner workings, showing how it leverages both distance and feature information.

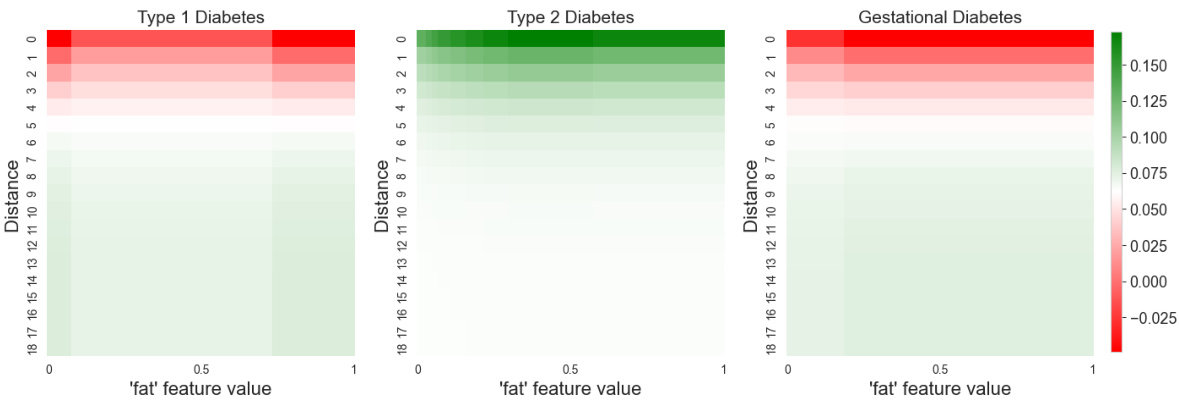
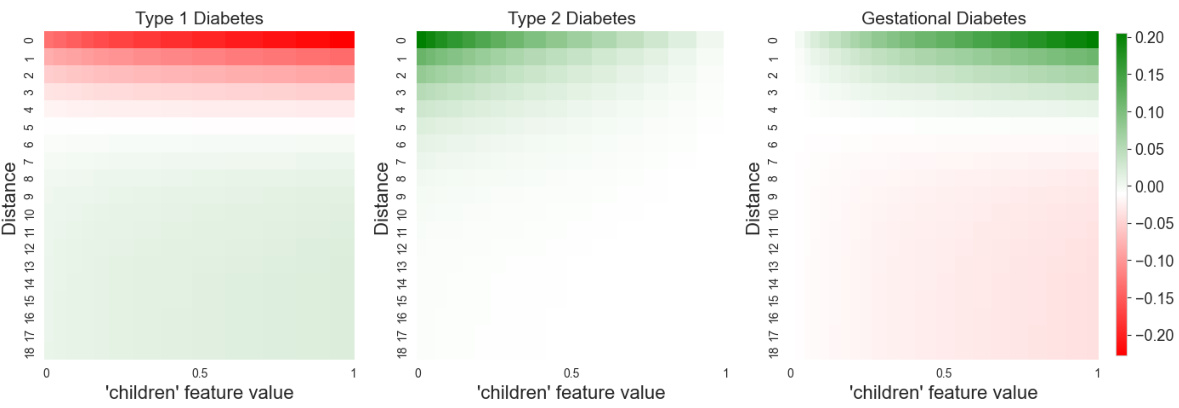
This figure visualizes the interaction between the ‘fat’ feature and distance in predicting the three types of diabetes. The heatmaps show how the importance of the ‘fat’ feature changes with distance for each diabetes type. Warmer colors (red/green) indicate stronger positive/negative contribution to the prediction for each diabetes type. This allows for a detailed understanding of how the model utilizes the feature across different distances and how this impacts its classification of the diabetes types.

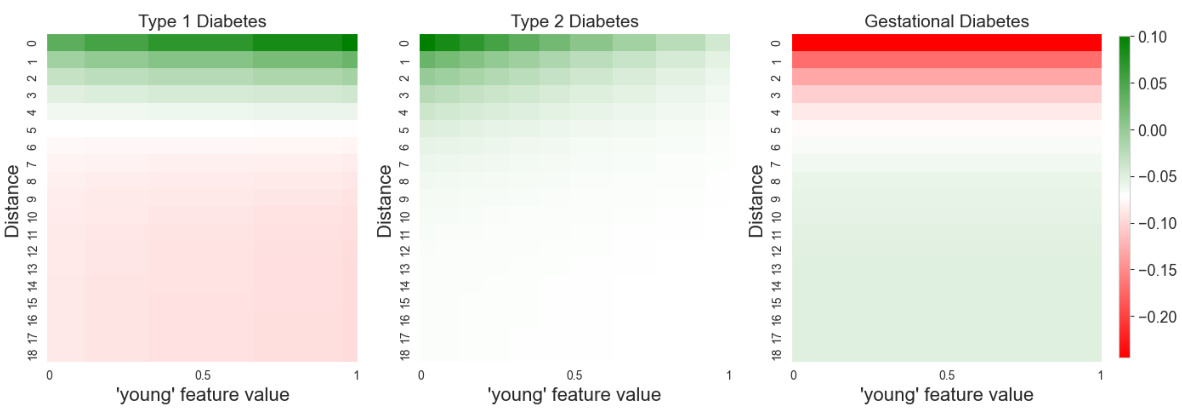
This figure visualizes the distance shape functions learned by the GNAN model for the PubMed dataset. Because there are three classes (type 1 diabetes, type 2 diabetes, and gestational diabetes), the output of the distance function is three-dimensional. The plot shows each of the three shape functions, facilitating a direct comparison. Notably, the functions indicate that the model primarily utilizes information from the local neighborhood of each node. Furthermore, the model’s behavior differs across the three classes: for type 2 diabetes, the influence diminishes as the distance increases, ultimately approaching zero; however, for type 1 and gestational diabetes, there is a negative effect with increasing distance.

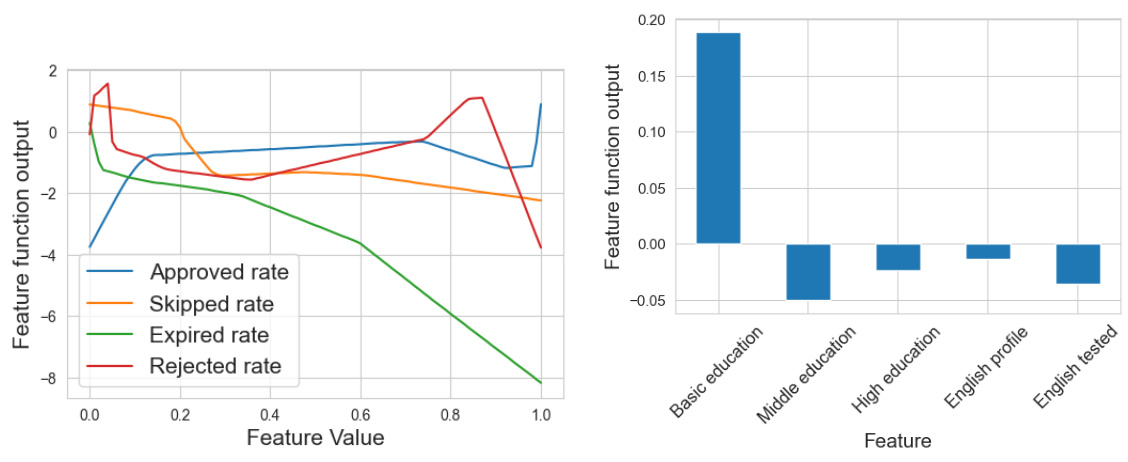
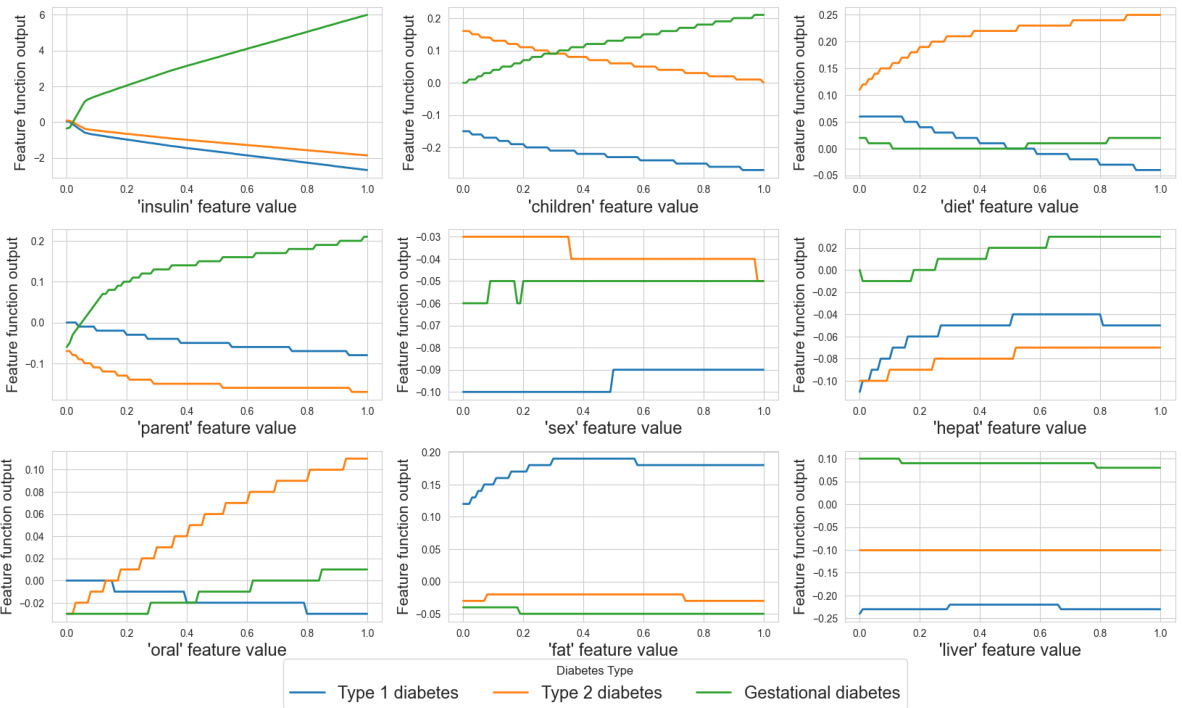
The figure visualizes the learned shape functions for nine features in the Tolokers dataset. Each line represents a different feature’s shape function, showing its non-linear relationship with the prediction. The x-axis represents the feature value, ranging from 0 to 1, and the y-axis shows the feature function output. The plot reveals how each feature contributes to the model’s prediction, illustrating non-monotonic relationships for some features.

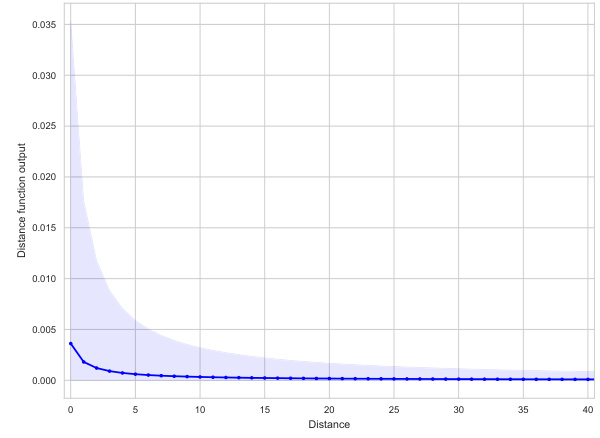
This figure shows the distance shape function learned by the GNAN model on the Tolokers dataset. The x-axis represents the distance between nodes in the graph, and the y-axis represents the output of the distance function. The plot shows how the model weighs the influence of nodes based on their distance. We can see that the model gives more weight to nodes that are closer, and less weight to nodes that are farther away. The shape of the function suggests that the model is able to learn complex relationships between nodes based on their distance.

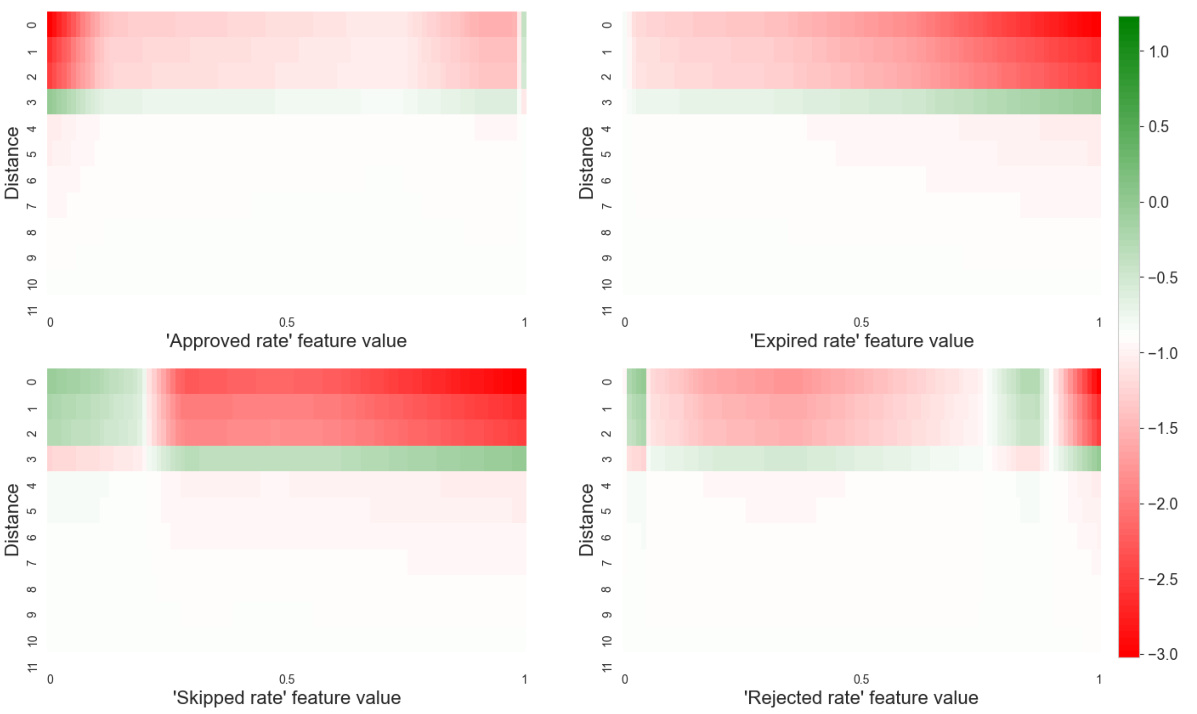
This heatmap visualizes the interaction between features and their distances from a node in the Mutagenicity dataset. The color of each cell represents the combined influence of a specific feature at a specific distance on the model’s prediction. Green indicates a positive contribution (increasing mutagenicity), while red shows a negative contribution (decreasing mutagenicity). This allows for a detailed understanding of how the model integrates both local feature information and the graph structure to make predictions.

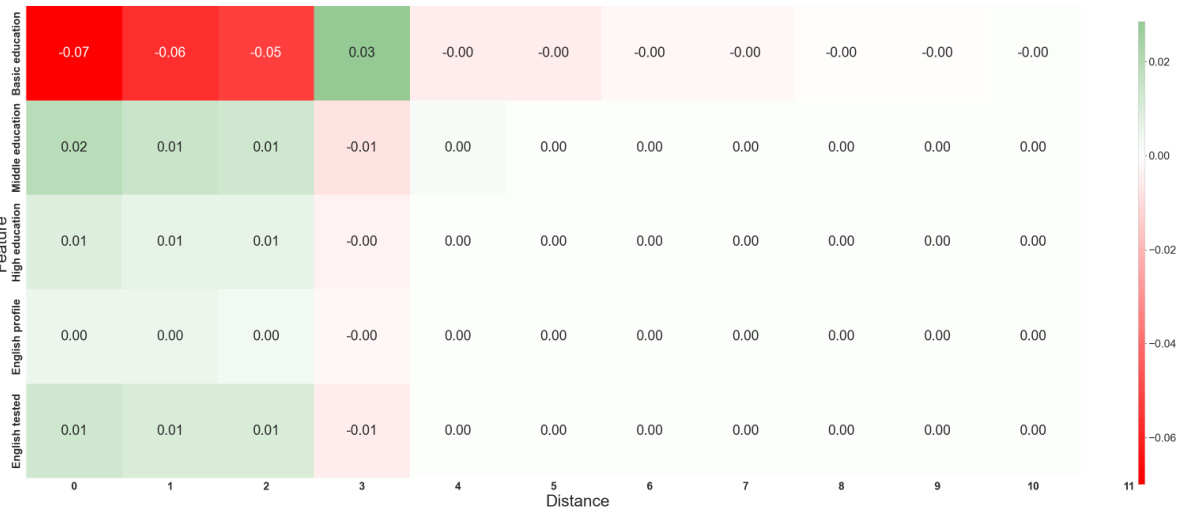
This heatmap visualizes the interplay between the distance and feature functions in the GNAN model trained on the Mutagenicity dataset. Each cell represents the combined effect of a specific feature at a particular distance on the model’s prediction. Positive values (green) indicate a contribution towards classifying a molecule as mutagenic, while negative values (red) suggest a contribution towards classifying it as non-mutagenic. The heatmap provides insight into how the model integrates both local features and the graph structure to make predictions.

Full paper

#