↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many imaging applications involve inferring an unknown image from limited, noisy measurements. Score-based diffusion models have shown promise as expressive image priors but incorporating them efficiently and robustly into diverse reconstruction tasks remains challenging. Existing methods often lack either efficiency, consistency, or robustness, particularly for nonlinear problems.
This paper introduces a novel algorithm, DPnP, that leverages the power of score-based diffusion models. DPnP cleverly integrates two samplers: a proximal consistency sampler focusing on measurement fidelity, and a denoising diffusion sampler utilizing the score functions of the image prior for regularization. The authors establish both asymptotic and non-asymptotic guarantees for DPnP, demonstrating its robustness and effectiveness in various tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a provably robust method for nonlinear inverse problems using a novel algorithmic framework. It addresses the limitations of existing approaches by providing both asymptotic and non-asymptotic performance guarantees, opening new avenues for research in various imaging applications and related fields. The work also contributes a new plug-and-play algorithm (DPnP), which is highly versatile and adaptable to diverse applications.
Visual Insights#

This figure shows examples of image reconstruction results using the proposed Diffusion Plug-and-Play (DPnP) method on three different types of inverse problems: super-resolution (linear), phase retrieval (nonlinear), and quantized sensing (nonlinear). For each problem, the input (noisy measurements) is shown on the left, and the corresponding reconstruction results from DPnP and other competing methods are shown alongside the ground truth image. The results visually demonstrate DPnP’s capability to solve both linear and nonlinear inverse problems.
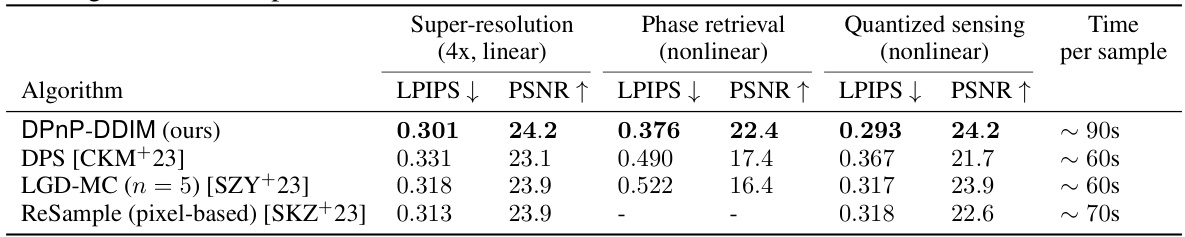
This table presents a comparison of different algorithms for solving three inverse problems: super-resolution, phase retrieval, and quantized sensing, using the FFHQ dataset. The algorithms compared are DPnP-DDIM (the proposed method), DPS, LGD-MC, and ReSample. The evaluation metrics are LPIPS and PSNR. The results show that DPnP-DDIM achieves competitive performance, particularly in phase retrieval where other methods struggle. The table highlights the computational cost per sample for each algorithm.
In-depth insights#
Diffusion Posterior#
The concept of “Diffusion Posterior” blends the generative power of diffusion models with the inferential framework of Bayesian methods. Diffusion models excel at generating realistic samples from complex distributions, learning to reverse a diffusion process that gradually adds noise to data. A “diffusion posterior” leverages this learned generative process as a prior distribution in a Bayesian setting to solve inverse problems. Instead of directly optimizing for an image, the approach samples from a posterior distribution that incorporates both the likelihood of the observed data and the prior knowledge encoded by the diffusion model. This offers advantages in handling ill-posed inverse problems, where the data alone is insufficient, and offers a principled way to quantify uncertainty in reconstruction results. A key challenge lies in efficiently sampling from the often high-dimensional posterior, requiring sophisticated sampling techniques and careful consideration of computational cost. The theoretical analysis of such methods is crucial, investigating the convergence properties and robustness to noise or imperfect score estimation, which are key elements of a diffusion posterior framework.
Plug-and-Play#
The concept of “Plug-and-Play” in image reconstruction signifies modularity and flexibility. It emphasizes the ability to integrate pre-trained components, like denoisers, into a larger image reconstruction framework without requiring extensive retraining or modification of the entire system. This approach contrasts with end-to-end methods that demand task-specific training. A key advantage of Plug-and-Play is its adaptability to diverse forward models and noise characteristics, making it a powerful tool for solving a broad range of inverse problems in imaging. However, theoretical understanding and performance guarantees often lag behind empirical success, posing a challenge for robust applications. The core idea is to leverage the strengths of independently developed components, thereby facilitating efficient algorithm design and customization.
Robustness#
The concept of robustness in the context of score-based diffusion models for image reconstruction is multifaceted. A robust method should demonstrate reliable performance despite noisy or incomplete measurements, variations in the forward model, and errors in score function estimation. The paper establishes robustness through theoretical guarantees, proving asymptotic convergence to the true posterior distribution under ideal conditions. More importantly, non-asymptotic bounds are derived, quantifying the graceful degradation of performance as the accuracy of score functions and samplers decreases. This theoretical robustness is then validated through numerical experiments, showing that the proposed DPnP method outperforms existing state-of-the-art techniques across various tasks with different complexities and levels of noise, showcasing its practical robustness.
Theoretical Guarantees#
The section on “Theoretical Guarantees” is crucial for establishing the paper’s contribution to the field. It likely presents asymptotic and non-asymptotic analyses of the proposed algorithm’s performance. Asymptotic analysis might show convergence to the true posterior distribution under ideal conditions, while non-asymptotic analysis would offer error bounds that depend on factors like the number of iterations or the accuracy of score function estimations. The presence of both analyses demonstrates a rigorous approach to validation and provides practical insight into the algorithm’s behavior in real-world scenarios. This is particularly important as the algorithm uses score-based diffusion models, which are often complex and challenging to analyze. The robustness analysis is especially valuable because it suggests how gracefully performance degrades as certain assumptions are violated. Overall, this section is essential for justifying the claims of the paper and highlighting its superiority compared to existing methods, by showing that not only does it work well empirically, but that there is a strong theoretical foundation underlying its operation.
Future Directions#
Future research could explore several promising avenues. Extending DPnP to more complex forward models beyond the scope of this paper, such as those with non-Gaussian noise or non-differentiable likelihoods, would significantly broaden its applicability. Developing more efficient sampling strategies for the denoising diffusion process could enhance DPnP’s computational performance. This could involve investigating alternative numerical methods or exploring the use of learned samplers. Combining DPnP with other techniques such as variational inference or Bayesian optimization could yield improved performance, especially for high-dimensional inverse problems. Finally, further theoretical analysis would help establish the optimality and robustness of DPnP under various conditions. Specifically, investigating the impact of imperfect score function estimates and understanding the limitations of the plug-and-play framework could be valuable.
More visual insights#
More on figures

This figure showcases the results of applying the Diffusion Plug-and-Play (DPnP) method to three different types of inverse problems: super-resolution (a linear problem), phase retrieval (a nonlinear problem), and quantized sensing (a nonlinear problem). For each problem, it shows the input (noisy measurements), and the reconstructions obtained using DPnP, compared to the ground truth. The results demonstrate the ability of DPnP to effectively reconstruct images from limited and noisy measurements across different problem types and nonlinearities.

This figure demonstrates the effectiveness of the proposed Diffusion Plug-and-Play (DPnP) method in solving various inverse problems. It showcases results for three different tasks: super-resolution (a linear inverse problem), phase retrieval (a nonlinear inverse problem), and quantized sensing (a nonlinear inverse problem). Each column represents a different method, with DPnP showing significantly improved results compared to the other methods. This highlights the method’s ability to handle both linear and nonlinear inverse problems and its versatility in different imaging modalities.

This figure shows the results of applying the proposed Diffusion Plug-and-Play (DPnP) method to three different inverse problems: super-resolution (a linear inverse problem), phase retrieval (a nonlinear inverse problem), and quantized sensing (a nonlinear inverse problem). For each problem, the input (noisy or incomplete measurements) is shown on the far left, followed by the reconstruction results from four different methods: DPS, LGD-MC, ReSample, and DPnP (using both DDPM and DDIM samplers). The ground truth image is shown on the far right. The figure visually demonstrates the ability of DPnP to effectively handle both linear and nonlinear inverse problems, and achieve superior performance compared to existing state-of-the-art methods.
More on tables
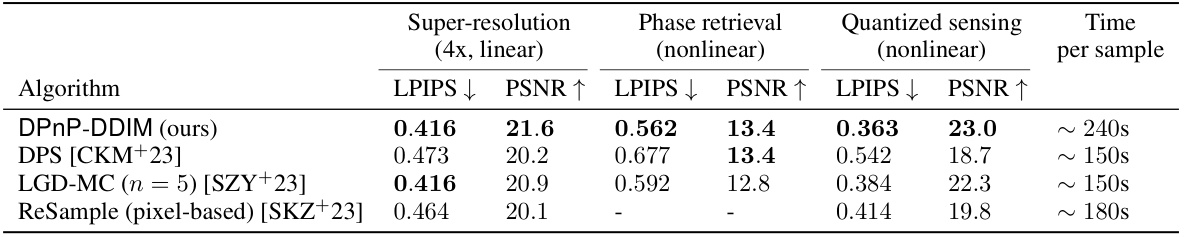
This table presents the quantitative results of evaluating different image reconstruction algorithms on the ImageNet dataset. The algorithms are compared across three inverse problem tasks: super-resolution, phase retrieval, and quantized sensing. The metrics used for comparison are LPIPS and PSNR. The table highlights that the proposed DPnP-DDIM method achieves superior performance compared to existing methods across all tasks, except for the ReSample algorithm which failed to produce meaningful results for phase retrieval. Computation time per sample is also provided for each algorithm.

This table compares the number of neural function estimations (NFEs) required for different algorithms (DPnP-DDIM, DPnP-DDPM, DPS, LGD-MC, and ReSample) to generate samples. NFEs represent the computational cost in terms of the number of calls to score functions. The values shown are approximate and vary depending on factors like initialization and the annealing schedule used in DPnP.
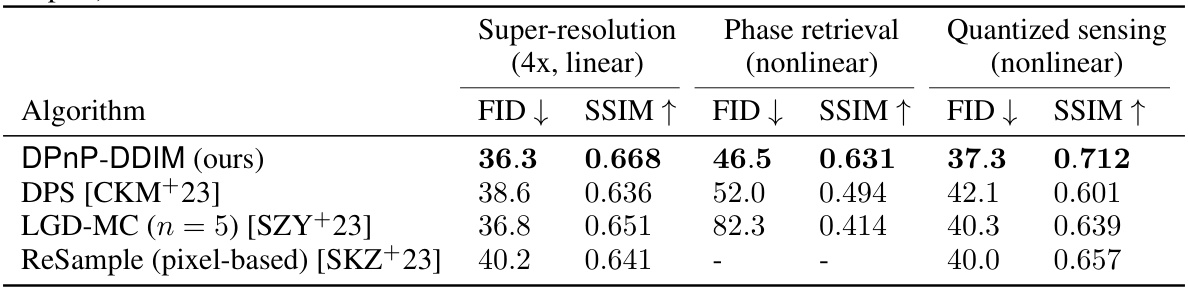
This table presents a comparison of the Fréchet Inception Distance (FID) and Structural Similarity Index Measure (SSIM) scores for four different algorithms applied to three inverse problems: super-resolution, phase retrieval, and quantized sensing. Lower FID scores indicate better performance, while higher SSIM scores indicate better performance. The results show that the DPnP-DDIM algorithm achieves better or comparable results than the other algorithms in each inverse problem.
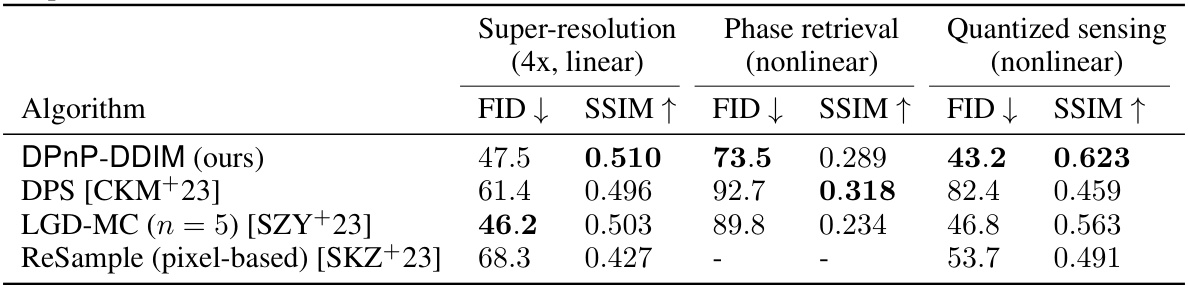
This table shows the Fréchet Inception Distance (FID) and Structural Similarity Index Measure (SSIM) scores for four different algorithms on the FFHQ dataset, solving three different inverse problems: super-resolution (linear), phase retrieval (nonlinear), and quantized sensing (nonlinear). Lower FID and higher SSIM values indicate better performance. The results demonstrate the relative performance of DPnP-DDIM compared to other state-of-the-art algorithms.
Full paper#