Achieving Tractable Minimax Optimal Regret in Average Reward MDPs

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it presents the first tractable algorithm achieving minimax optimal regret for average-reward Markov Decision Processes (MDPs), a significant advancement in reinforcement learning. It addresses a long-standing computational challenge and provides a novel subroutine applicable to other RL algorithms, paving the way for improved efficiency and theoretical guarantees. This has significant implications for various applications of RL.

Visual Insights

#

This figure provides a visual representation of the algorithm PMEVI-DT and how its regret is analyzed. It breaks down the total regret into four main components: navigation error, empirical bias error, optimistic overshoot, and second-order error. Each component is linked to a specific lemma in the paper that details its theoretical bound. The figure shows how these components contribute to the overall regret of the algorithm, illustrating the different sources of error and their respective magnitudes. The diagram effectively summarizes the key steps of the regret analysis presented in the paper. It visually clarifies the relationships between different sources of errors, and also shows that the analysis takes into consideration several scenarios and the different errors in each one. The use of a diagram is beneficial as a summarization of the theoretical contributions, and aids in grasping the main points of the paper.

This table compares the performance of several reinforcement learning algorithms used for average-reward Markov Decision Processes (MDPs). It lists various characteristics for each algorithm, including the regret bound (a measure of performance), whether it is computationally tractable, and any specific requirements or assumptions made. The regret bound is expressed using several variables: S (number of states), A (number of actions), T (number of steps), D (diameter of the MDP, or local diameter Ds), and sp(h*) (span of the optimal bias function). Other details such as Bayesian regret, requirements for knowledge of sp(h*), and comments about specific algorithm properties are also included.

In-depth insights

#

Minimax Regret

#

Minimax regret, a core concept in online learning, particularly relevant to reinforcement learning, seeks to minimize the worst-case regret an algorithm can experience. In the context of Markov Decision Processes (MDPs), it balances exploration (gathering information) and exploitation (using that information). The minimax approach focuses on finding algorithms that perform optimally even under the most challenging conditions, hence the term “worst-case”. This is especially crucial in average-reward MDPs, which lack the convenient reset mechanism of episodic MDPs, making long-term performance optimization more challenging. Achieving minimax optimal regret often requires a careful design of exploration strategies and the use of sophisticated techniques like optimism in the face of uncertainty. Tractability is a significant concern; while theoretical bounds provide valuable guarantees, practically usable algorithms must have polynomial time complexity. The paper’s contribution lies in developing a tractable algorithm that guarantees minimax optimal regret, overcoming the computational challenges faced by previous approaches. This advancement is significant because it bridges the gap between theory and practice, allowing the application of theoretically sound methods to real-world problems.

PMEVI Subroutine

#

The PMEVI subroutine, Projected Mitigated Extended Value Iteration, is a crucial innovation enhancing the efficiency and optimality of reinforcement learning algorithms for average reward Markov Decision Processes (MDPs). Its core functionality involves efficiently computing near-optimal policies under uncertainty by leveraging bias information. Unlike prior approaches that rely on computationally expensive or suboptimal methods, PMEVI incorporates bias constraints and a mitigation technique to refine the Extended Value Iteration (EVI) process, achieving a significant improvement. The projection step ensures the solution remains within a predefined bias region, while mitigation addresses the uncertainty of the unknown environment. This approach results in a tractable algorithm achieving minimax optimal regret, a critical metric showing the algorithm performs as well as possible considering the worst possible scenario. The subroutine’s effectiveness stems from the efficient integration of bias information and variance reduction techniques leading to a polynomial time algorithm with improved regret bounds, unlike previously intractable approaches. In essence, PMEVI is a pivotal contribution offering a significant advancement in efficiently solving average reward MDPs.

Bias Confidence

#

The concept of ‘Bias Confidence’ in reinforcement learning, particularly within the context of average reward Markov Decision Processes (MDPs), is crucial for achieving optimal regret bounds. It involves quantifying the uncertainty in estimating the optimal bias function, which represents the long-term accumulated reward difference between starting in different states. A high bias confidence implies a more precise estimate of the bias function, leading to more informed decision-making and reduced regret. The challenge lies in efficiently constructing this bias confidence region while maintaining computational tractability. This often involves balancing exploration (gathering data to improve the estimate) and exploitation (using the current estimate to make decisions). Accurate bias confidence is vital for algorithms aiming to achieve minimax optimal regret. Effective methods leverage various techniques such as confidence bounds derived from concentration inequalities, incorporating prior knowledge about the bias function, and employing efficient bias estimation subroutines. The design of the bias confidence region significantly impacts the algorithm’s performance and theoretical guarantees; a poorly designed region can lead to suboptimal regret, while an overly conservative one might cause computational inefficiencies. Therefore, striking a balance between accuracy and tractability is key to successful algorithm design in this domain.

Regret Analysis

#

Regret analysis in reinforcement learning is crucial for evaluating the performance of algorithms. It quantifies the difference between an algorithm’s cumulative reward and that of an optimal policy that knows the environment perfectly. The core idea is to decompose the regret into manageable components, often using techniques like optimism in the face of uncertainty or pessimism. A key challenge lies in handling the exploration-exploitation trade-off, as exploration is needed to learn the environment but leads to immediate sub-optimal actions. The analysis often involves concentration inequalities to bound the deviation of estimated quantities from their true values, ultimately leading to regret bounds that depend on the problem’s characteristics, such as the size of the state-action space and the horizon. Tight regret bounds are highly desirable, indicating algorithm efficiency. The analysis can be complex, especially for average-reward Markov Decision Processes (MDPs), which lack a natural terminal state, requiring innovative techniques to handle the bias and gain. Advanced techniques often incorporate confidence regions around the unknown environment, utilizing optimism or other strategies to select actions. The ultimate goal is to achieve minimax optimal regret, meaning the algorithm performs as well as theoretically possible, regardless of the environment’s specific structure.

Future Work

#

The paper’s conclusion suggests several promising avenues for future research. Improving the bias estimation mechanism is crucial; the current method struggles in early learning phases, hindering practical performance despite theoretical optimality. Exploring alternative confidence regions could improve computational efficiency and empirical results, as the choice of region currently impacts performance. Investigating the interaction between the bias confidence region and the choice of mitigation technique could lead to refinements in the algorithm’s design and further enhance regret bounds. Finally, extending the theoretical analysis to broader classes of MDPs beyond weakly-communicating ones would significantly broaden the algorithm’s applicability and impact.

More visual insights

#

More on figures

The figure consists of two subfigures. The left subfigure shows the performance comparison of UCRL2 and PMEVI-DT algorithms on a 3-state river-swim environment. PMEVI-DT is tested with different levels of prior knowledge about the bias function. The right subfigure shows the comparison of several algorithms (UCRL2, KL-UCRL, UCRL2B and their PMEVI variants) on a 5-state river-swim environment.

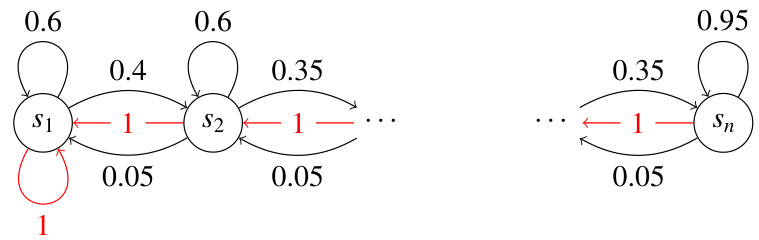
This figure shows the transition probabilities between states in a river-swim Markov Decision Process (MDP). In this MDP, there are n states arranged linearly. The agent can choose to move either RIGHT or LEFT. The transition probabilities are depicted by arrows between states, labeled with probabilities. Rewards are Bernoulli, with a reward of 0.95 only for the action RIGHT in the final state (s_n) and a reward of 0.05 only for the action LEFT in the initial state (s₀). All other state-action pairs yield a reward of 0.

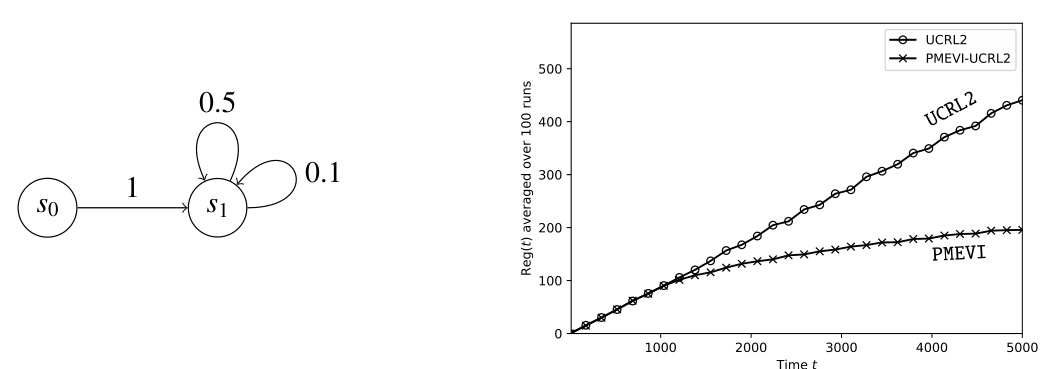
The left graph shows the regret of UCRL2 and PMEVI-DT (with different prior knowledge) on a 3-state river-swim environment. The right graph compares several algorithms’ average regret (UCRL2, KL-UCRL, UCRL2B) against their PMEVI-enhanced versions on a 5-state river-swim environment. The graphs illustrate the impact of prior knowledge and PMEVI subroutine on regret performance.

More on tables

This table compares various reinforcement learning algorithms for average-reward Markov Decision Processes (MDPs). It shows the regret bounds achieved by each algorithm, indicating their efficiency in terms of the number of steps (T), state-action space (SxA), diameter (D), and bias span (sp(h*)). It also notes whether the algorithms are tractable and what prior knowledge, if any, is required. The table helps illustrate the state-of-the-art and the improvement achieved by the proposed PMEVI-DT algorithm.

This table compares various reinforcement learning algorithms for average-reward Markov Decision Processes (MDPs). It shows the regret bounds achieved by each algorithm, indicating their performance in terms of time and space complexity. Key parameters include the size of the state-action space (SxA), total steps (T), diameter (D or Ds), bias span (sp(h*)), mixing time (tmix), and hitting time (thit). The table also notes whether each algorithm is tractable and the prior knowledge required.

This table compares different reinforcement learning algorithms for average-reward Markov Decision Processes (MDPs). It shows the regret bounds achieved by each algorithm, indicating their computational tractability and whether they require prior knowledge of the MDP. Key parameters influencing the regret are also included, such as the size of the state-action space, the number of steps, the diameter of the MDP, the span of the bias function, mixing time, and hitting time. The table helps to situate the proposed algorithm (PMEVI-DT) within the existing literature.

Full paper

#