The Impact of Initialization on LoRA Finetuning Dynamics

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in deep learning and large language model optimization. It directly addresses the critical issue of efficient fine-tuning, a major bottleneck in deploying LLMs. By providing a rigorous theoretical analysis and empirical validation of initialization strategies within LoRA, this research offers practical guidelines for improved performance and opens up new avenues for exploring parameter-efficient methods. Its findings could significantly impact the development and application of LLMs, making them more accessible and efficient for a wider range of researchers and practitioners.

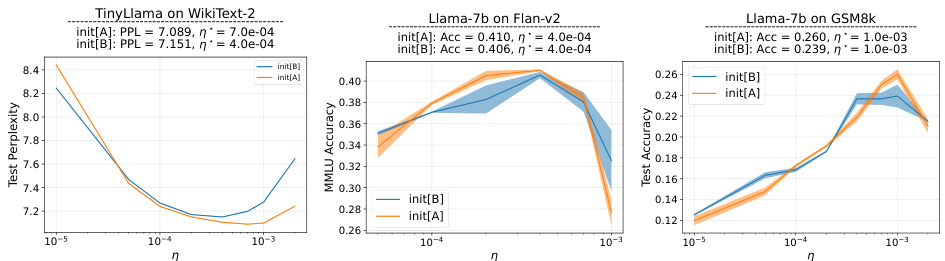
Visual Insights

#

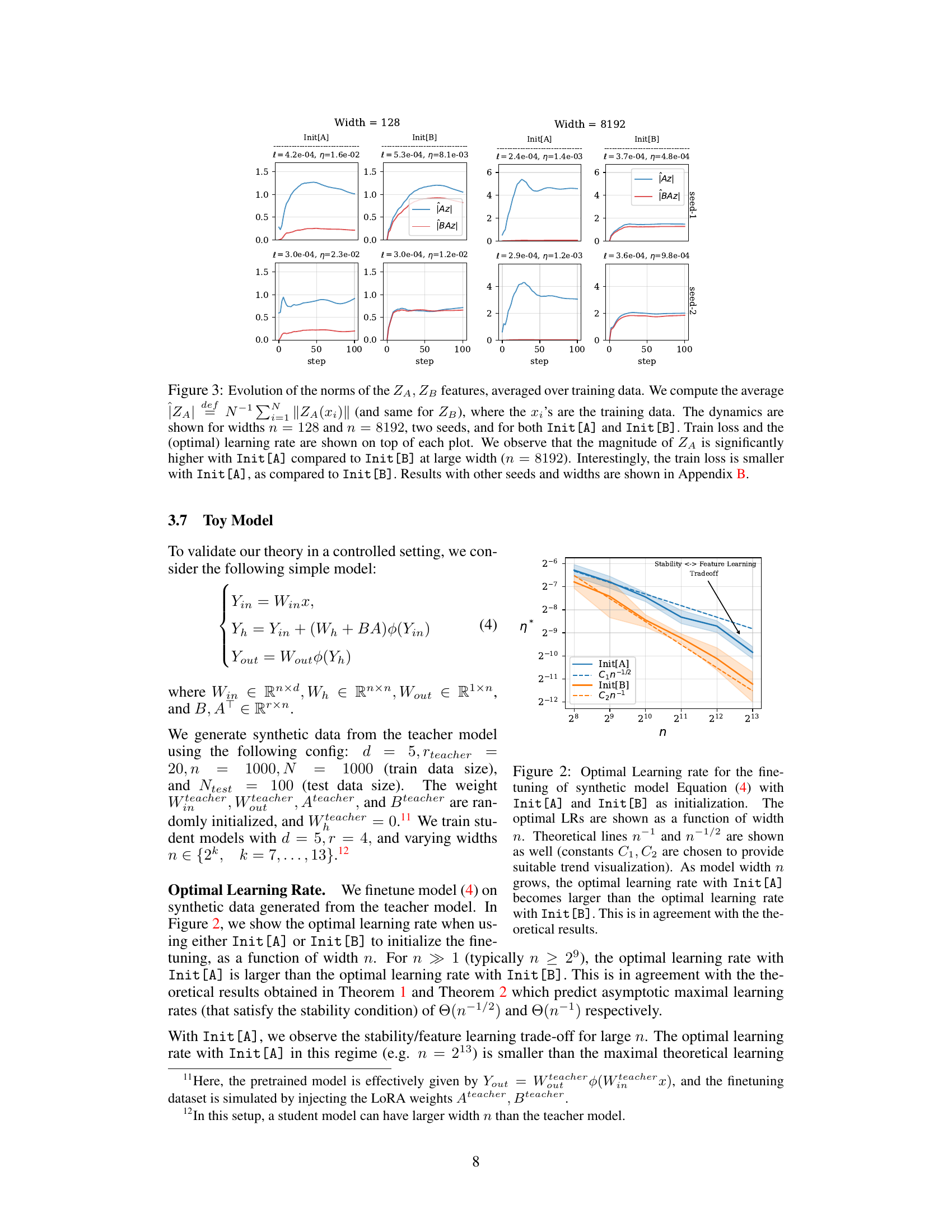
This figure summarizes the key findings of the paper regarding the impact of initialization on LoRA finetuning. It compares two initialization schemes, Init[A] and Init[B], showing their effects on optimal learning rate, finetuning dynamics, and overall performance. Init[A], which initializes B to zero and A to random, generally leads to better performance due to more efficient feature learning, although with some instability. Init[B] provides stability but suffers from suboptimal feature learning. The figure visually represents the differences in the learning processes and the resulting performance.

This table details the hyperparameters and settings used for training RoBERTa-Large models on GLUE tasks using the LoRA method. It specifies the model, learning rates, beta values for AdamW optimizer, epsilon, learning rate schedule, weight decay, training batch size, number of epochs, LoRA rank, alpha, dropout, target modules, sequence length, random seeds, and precision. These parameters define the specific configurations of the experiments conducted in the study.

In-depth insights

#

LoRA Init. Impact

#

The study’s core finding is that the seemingly minor choice of initializing either the A or B matrix in LoRA to zero significantly impacts model training. Initializing B to zero (Init [A]) consistently outperforms initializing A to zero (Init [B]), achieving better results with larger learning rates. This is not merely empirical; the authors provide a theoretical analysis using the large-width limit of neural networks to explain why Init [A] allows for more efficient feature learning and greater stability. Init [A]’s success stems from the introduction of a controlled level of instability, enabling faster learning without compromising overall performance. Conversely, Init [B] suffers from suboptimal feature learning, unable to leverage larger learning rates effectively. The paper provides empirical validation across various language models and datasets, confirming the theoretical findings and suggesting a straightforward yet crucial improvement to the standard LoRA training procedure.

Large-Width Analysis

#

Large-width analysis, a crucial technique in the study of neural networks, offers valuable insights into the behavior of LoRA (Low-Rank Adaptation) finetuning. By examining the infinite-width limit, researchers can derive principled scaling rules for hyperparameters, like learning rates and initialization schemes. This approach helps to avoid numerical instabilities and facilitates efficient learning. Specifically, the analysis reveals a crucial trade-off between stability and feature learning in LoRA finetuning, which is highly sensitive to initialization choices. Init[A], while leading to more efficient learning and use of larger learning rates, can result in ‘internal instability,’ where some internal features grow unbounded, whereas Init[B] is more stable but achieves suboptimal feature learning. This large-width analysis provides a theoretical framework for understanding the observed differences in LoRA finetuning dynamics and suggests that Init[A] is generally preferable despite its instabilities, especially at larger model widths. The insights from this analysis can be leveraged to optimize LoRA finetuning by helping practitioners to choose appropriate hyperparameter settings.

Init. & Learning Rate

#

The interaction between initialization and learning rate in the context of Low-Rank Adaptation (LoRA) for fine-tuning large language models is a crucial aspect of the paper. The authors explore two initialization schemes: Init[A], where one matrix is initialized randomly and another to zeros, and Init[B], the reverse. Init[A] demonstrably allows for larger learning rates compared to Init[B] without causing instability. This difference arises from the distinct dynamics they induce, impacting feature learning. While Init[A] leads to more efficient feature learning, it also suffers from internal instability where the internal features grow without unbounded growth in output. Init[B] is more stable, however this comes at the cost of suboptimal feature learning because the learning rate cannot be increased sufficiently. This trade-off highlights the importance of considering initialization strategies when optimizing the training process.

LLM Finetuning

#

LLM finetuning, a crucial aspect of large language model adaptation, focuses on enhancing pretrained models for specific tasks. Parameter-efficient techniques, like LoRA, are vital due to the computational cost of training massive LLMs. This paper investigates the impact of initialization strategies on LoRA’s finetuning dynamics. The choice between initializing matrix A or B to zero significantly affects the learning process and final performance. A theoretical analysis reveals that initializing B to zero (Init[A]) allows for larger learning rates, leading to more efficient feature learning, though it may introduce ‘internal instability’. Conversely, initializing A to zero (Init[B]) provides stability but suffers from suboptimal feature learning. Experimental results on various LLMs and datasets validate these findings, demonstrating that Init[A] generally produces superior outcomes. Further research should explore the trade-off between stability and efficiency, and how techniques like LoRA+ might address the limitations of both initialization schemes.

Future Work

#

The paper’s findings on LoRA initialization suggest several promising avenues for future research. A key area is bridging the gap between the theoretical large-width analysis and finite-width practical observations. While the theory provides valuable insights into the dynamics of Init[A] and Init[B], further investigation is needed to understand how these dynamics manifest in models of realistic sizes. Exploring the interaction between LoRA initialization and other parameter-efficient fine-tuning techniques like LoRA+ is crucial. This could lead to more robust and efficient training methods. Another important direction is developing a more comprehensive understanding of the ‘internal instability’ observed with Init[A]. Determining the optimal balance between this instability and efficient feature learning is key for achieving optimal performance. Finally, the paper highlights the need for more systematic experiments across diverse language models and downstream tasks. This would strengthen the generalizability of the findings and provide a clearer picture of LoRA’s behavior in various settings.

More visual insights

#

More on figures

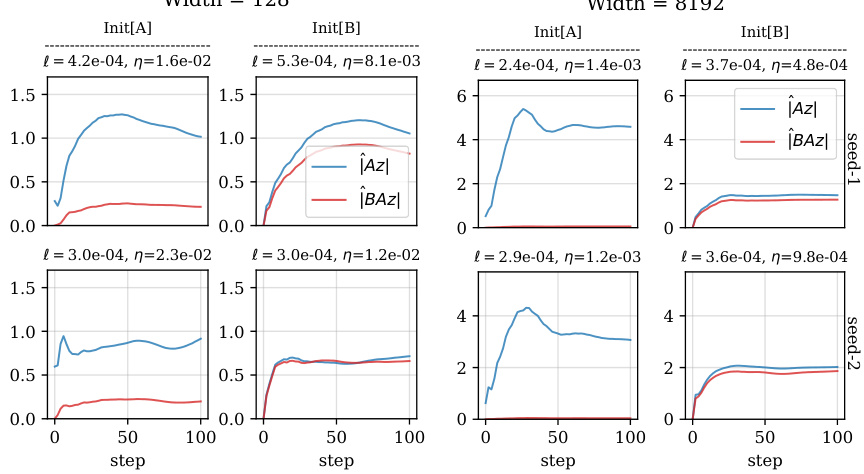
This figure shows the evolution of the norms of the LoRA features Z_A and Z_B during training, averaged over the training data points. It compares two different initialization schemes (Init[A] and Init[B]) for two different network widths (n = 128 and n = 8192). The plots illustrate that the magnitude of Z_A is substantially larger with Init[A] than with Init[B], especially for the larger network width. Despite this, the training loss is lower with Init[A], suggesting a tradeoff between feature magnitude and training loss. The figure also includes the optimal learning rates used for each initialization and network width.

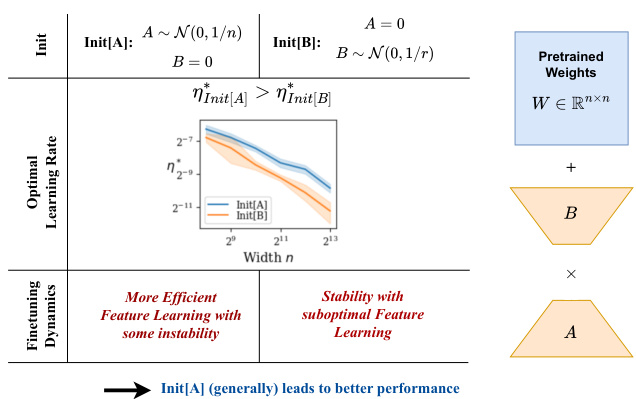
This figure shows the optimal learning rate for a synthetic model as a function of model width, comparing two different initialization schemes (Init[A] and Init[B]). The plot shows that as the model width increases, the optimal learning rate for Init[A] becomes significantly larger than for Init[B]. Theoretical lines representing the scaling laws of n⁻¹ and n⁻¹/² are included for comparison, demonstrating agreement with the theoretical analysis presented in the paper.

This figure shows the evolution of the norms of the LoRA features ZA and ZB during training, averaged across training data points. It compares two different initialization schemes (Init[A] and Init[B]) at different network widths (n=128 and n=8192). The results demonstrate that the magnitude of ZA is substantially larger with Init[A] than with Init[B], especially at larger widths. Despite this, the training loss is lower with Init[A], suggesting a trade-off between feature magnitude and training loss.

This figure displays the evolution of the norms of ZA and ZB features during training, averaged across training datapoints. It compares two initialization schemes, Init [A] and Init [B], at different network widths (n=128 and n=8192) and random seeds. The plots reveal that the magnitude of ZA is considerably larger with Init [A] than with Init [B], especially at larger network widths. This difference is interesting because the training loss is lower with Init [A].

This figure shows the evolution of the norms of the LoRA features ZA and ZB during training, averaged across training data points. It compares two initialization schemes, Init [A] and Init [B], across different network widths (n = 128 and n = 8192) and random seeds. The plots illustrate how the magnitude of ZA is considerably larger with Init [A] than with Init [B], especially at a larger width (n=8192). Despite this, the training loss is lower for Init [A], suggesting that while Init [A] exhibits higher internal instability, it achieves better performance.

More on tables

This table shows the hyperparameters used for the Low-Rank Adaptation (LoRA) method in the experiments described in the paper. The LoRA rank determines the dimensionality of the low-rank approximation used to adapt the model parameters. LoRA α is a scaling factor. LoRA Dropout refers to the dropout rate used during training to regularize the model. Finally, Target Modules specifies which modules of the model are adapted using the LoRA technique.

This table lists the hyperparameters used for the Low-Rank Adaptation (LoRA) experiments in the paper. It details settings like the rank of the LoRA matrices, the alpha scaling factor, dropout rate, and which modules were targeted for adaptation. These settings are crucial to the parameter efficiency of LoRA and influence its performance.

This table details the training algorithm used for the experiments, specifically focusing on hyperparameters like learning rates, betas for AdamW optimizer, epsilon value, learning rate schedule, weight decay, batch size, and number of epochs. These settings are consistent across various model and dataset combinations, except where otherwise specified in the paper.

This table lists the hyperparameters used for the Low-Rank Adaptation (LoRA) method in the experiments. It specifies the rank of the low-rank matrices (LoRA Rank), the scaling factor for the rank decomposition (LoRA α), the dropout rate applied to the LoRA layers (LoRA Dropout), and the specific modules within the language model that the LoRA adaptation is applied to (Target Modules). These settings are crucial for controlling the tradeoff between model performance and the number of trainable parameters.

This table lists the hyperparameters used in the experiments involving the TinyLlama model on the WikiText-2 dataset. It details the settings for the training algorithm (AdamW), including learning rates, beta values, epsilon, learning rate schedule, weight decay, batch size, number of epochs, and LORA parameters (rank, alpha, dropout, and target modules). Additionally, it provides hyperparameters for other aspects of the experiment, including sequence length, the number of random seeds used, and the precision (BF16).

This table details the hyperparameters used for training the Llama-7b model on the GSM8k dataset. It specifies the range of learning rates tested, the beta parameters for AdamW optimizer, epsilon value, learning rate schedule, weight decay, training batch size, and the number of epochs.

This table shows the hyperparameters used for the Low-Rank Adaptation (LoRA) experiments in the paper. It lists the LoRA rank, the scaling factor alpha, the dropout rate, and the target modules that were updated during the training. These settings are crucial for the parameter-efficient fine-tuning of large language models, as detailed in the paper.

This table lists the hyperparameters used for the Low-Rank Adaptation (LoRA) experiments in the paper. It includes details like the rank of the LoRA matrices, the scaling factor, dropout rate, and which modules were targeted for adaptation.

This table shows the hyperparameters used for training the Llama-7b model on the GSM8k dataset. It lists the learning rates, beta1, beta2, epsilon values used in the AdamW optimizer, the learning rate schedule, weight decay, training batch size, and the number of epochs.

This table shows the hyperparameters used for the Low-Rank Adaptation (LoRA) experiments in the paper. The LoRA rank specifies the dimensionality reduction applied to the weight matrices. LoRA α is a scaling factor for the update of the LoRA matrices. LoRA Dropout refers to the dropout rate used during training of the LoRA weights. Finally, Target Modules specifies the layers within the model to which LoRA is applied.

This table lists the hyperparameters used in the experiments described in section 4.1 of the paper. These hyperparameters were used for fine-tuning the RoBERTa-large model on GLUE tasks using LORA. The table includes details about sequence length, random seeds, and precision settings.

Full paper

#