↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
The increasing size and computational cost of machine learning models necessitate model compression techniques. Existing methods often lack theoretical grounding, particularly in neural network (DNN) pruning where heuristics based on Optimal Brain Surgeon (OBS) have dominated. While these heuristic methods have shown promise, the connection to the established field of sparse recovery remains unexplored, potentially limiting improvements.
This paper introduces Iterative Optimal Brain Surgeon (I-OBS), a new family of algorithms that leverages second-order information to enhance the efficiency of iterative sparse recovery algorithms. I-OBS offers theoretical convergence guarantees, unlike previous methods, and demonstrates superior performance through extensive experiments on Transformer-based DNNs applied to vision and language tasks. The proposed method shows I-OBS not only achieves superior results compared to current methods, but also provides a theoretical framework for future model compression research.
Key Takeaways#
Why does it matter?#
This paper is important because it bridges the gap between two seemingly disparate areas: sparse recovery algorithms and neural network pruning. By combining theoretical guarantees with practical algorithms and large-scale experiments, it offers new avenues for improving the efficiency and accuracy of machine learning models, a crucial area for current research.
Visual Insights#

This figure compares the performance of two algorithms, k-IHT and Topk-I-OBS, on a sparse linear regression task using two different prior distributions (standard Gaussian and MNIST). The left panel shows the training loss curves for both algorithms, demonstrating the convergence rate of each. The right panel displays the L2 distance between the solution found by each algorithm and the true optimal solution. The shaded regions represent the variability across multiple runs. The results suggest that Topk-I-OBS converges faster and achieves a solution closer to the optimum than k-IHT, especially when using the MNIST prior.

This table presents the Top-1 accuracy results on the ImageNet validation set for three different DeiT models (DeiT-Tiny, DeiT-Small, and DeiT-Base) using SparseGPT for pruning. It shows the accuracy for different numbers of iterations of the I-OBS algorithm, highlighting the impact of iterative pruning on model accuracy. The results demonstrate that I-OBS consistently improves accuracy across all model sizes, with larger improvements seen in smaller models and quickly saturating for larger models.
In-depth insights#
I-OBS: Algorithmic Core#
The core of the I-OBS algorithm centers around iteratively refining a sparse solution by leveraging second-order information. Unlike first-order methods, I-OBS incorporates curvature information, specifically the Hessian matrix, to guide the update process. This allows for a more informed decision about which parameters to prune or retain, leading to faster convergence and potentially higher accuracy. The algorithm begins with a dense model and iteratively refines it by approximating the loss function and strategically selecting a subset of parameters to adjust or remove. This selection, crucial to the effectiveness of I-OBS, uses second-order information to improve the choice. The algorithm offers a trade-off between computational cost and model accuracy. While theoretically rigorous, practical versions of I-OBS often employ approximations of the Hessian, balancing theoretical guarantees with computational efficiency. The success hinges on accurately modeling and exploiting the curvature of the loss landscape to accelerate convergence toward an optimal sparse solution. Efficient approximations of the Hessian are key to scaling I-OBS for large models.
Convergence Rates#
Analyzing convergence rates in machine learning algorithms is crucial for understanding their efficiency and scalability. Faster convergence translates to less computational time and energy consumption, making algorithms more practical for large-scale applications. Theoretical analysis of convergence rates often involves establishing bounds on the error between the algorithm’s iterates and the optimal solution, providing insights into how quickly the algorithm approaches its goal. Different algorithms exhibit different convergence behaviors, some converging linearly, others quadratically, or even sublinearly. The choice of algorithm depends on the specific problem and the desired level of accuracy. Factors influencing convergence rates include the properties of the objective function (e.g., convexity, smoothness), the algorithm’s parameters (e.g., step size, regularization), and the problem’s dimensionality. Empirical evaluation through experiments complements theoretical analysis, providing practical insights into algorithm performance in real-world scenarios. Investigating the interplay between these factors is key for developing and optimizing machine learning algorithms.
Model Sparsity#
Model sparsity, a crucial technique in modern machine learning, focuses on reducing model complexity by eliminating less important parameters. This is driven by the need to decrease computational costs, memory footprint, and energy consumption, especially for large models. The trade-off between sparsity and accuracy is a key consideration. Approaches range from simple heuristic methods to sophisticated optimization algorithms leveraging second-order information. Heuristic methods, while effective in practice, often lack a solid theoretical foundation. In contrast, optimization-based approaches, such as those inspired by the Optimal Brain Surgeon framework, aim for more principled solutions by utilizing information about loss curvature. These techniques, however, can be computationally expensive, especially at scale. Recent research emphasizes bridging the gap between heuristic and optimization-based methods, seeking algorithms that retain the practical effectiveness of heuristics while offering theoretical guarantees. This research area is actively evolving, with ongoing efforts to develop efficient, theoretically-sound sparse training and pruning methods for different model architectures and tasks. Future work will likely focus on addressing the scalability challenges of optimization-based methods while also exploring novel regularization techniques to better control the sparsity-accuracy trade-off.
Practical I-OBS#
A practical I-OBS algorithm would address the limitations of the theoretical I-OBS by focusing on computational efficiency and scalability. The core challenge lies in approximating the Hessian matrix, which is computationally expensive for large-scale models. A practical approach might involve using techniques like low-rank approximations or stochastic estimations of the Hessian, trading off some theoretical optimality for significantly faster computation. Additionally, a greedy heuristic for selecting the support set Qt+1 would replace the intractable optimal search. This heuristic might prioritize weights based on magnitude of the preconditioned gradient or other criteria for efficient pruning. The ultimate goal is to develop a faster converging algorithm capable of delivering accurate sparsity in realistic settings while maintaining good theoretical properties, providing guarantees on convergence rate and sparsity level, even if these guarantees are looser than those of the idealized theoretical version.
Future Research#
The paper’s success in bridging sparse recovery and Optimal Brain Surgeon (OBS) techniques opens several avenues for future work. Extending I-OBS to non-convex loss functions beyond quadratics would enhance applicability to broader machine learning models. Exploring adaptive sparsity levels during training, rather than a fixed k, could lead to improved performance and efficiency. The algorithm’s reliance on Hessian approximations warrants investigation into more efficient Hessian estimation techniques, particularly for large-scale models. Finally, a key area for future research is a rigorous theoretical analysis to relax strong assumptions currently needed for theoretical guarantees, making the approach more robust in practice. Investigating different sparsity-inducing penalties in place of the l0 norm could potentially improve convergence rates or computational efficiency.
More visual insights#
More on figures

This figure compares the performance of two algorithms, k-IHT and Topk-I-OBS, on a sparse linear regression task using two different priors: a standard Gaussian prior and an MNIST prior. The left subplot shows the learning curves (loss vs. iteration count) for both algorithms with the standard Gaussian prior, demonstrating Topk-I-OBS’s faster convergence rate. The right subplot visually presents the original MNIST digit images, images recovered using Topk-I-OBS, and images recovered using k-IHT for the MNIST prior; this illustrates the superior recovery quality of Topk-I-OBS.
This figure compares the performance of two algorithms, k-IHT and Topk-I-OBS, on a sparse linear regression task using two different priors (standard Gaussian and MNIST). The left subplot (a) shows the learning curves for both algorithms using the standard Gaussian prior, demonstrating the faster convergence of Topk-I-OBS. The right subplot (b) shows the reconstruction quality of the MNIST prior by both methods, visually comparing the recovered image with the original. The results highlight the superior convergence and reconstruction capabilities of Topk-I-OBS.

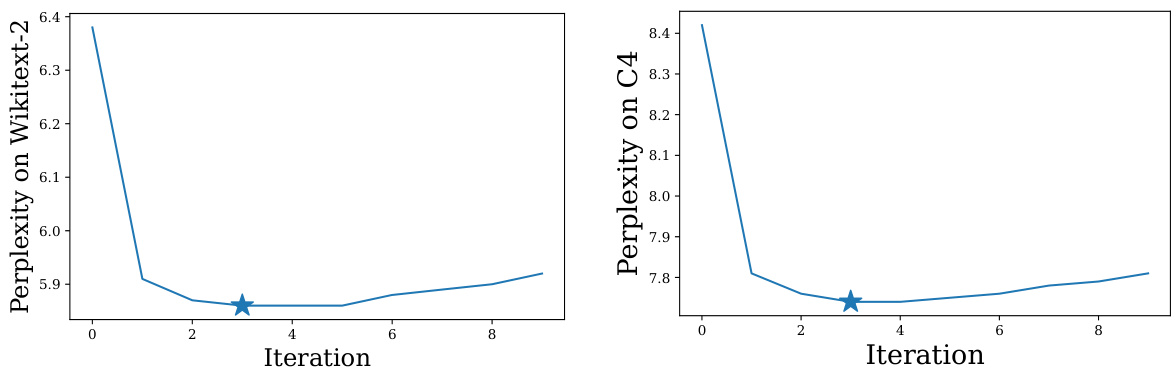
This figure shows the perplexity (a measure of how well a language model predicts a sequence of words) for the Llama-2 7B language model on two different datasets, WikiText-2 and C4. The x-axis represents the iteration number of the I-OBS (Iterative Optimal Brain Surgeon) algorithm, and the y-axis shows the perplexity. The left panel shows perplexity on the WikiText-2 dataset, while the right panel shows perplexity on the C4 dataset. The star indicates the iteration with the lowest perplexity score (best performance). The figure demonstrates how the perplexity changes over the iterations of the I-OBS algorithm. The initial decrease indicates improvement during pruning but is followed by an increase suggesting a possible overfitting to the training dataset in later iterations.
More on tables

This table presents the Top-1 accuracy results on the ImageNet validation set for three different DeiT models (DeiT-Tiny, DeiT-Small, and DeiT-Base) after applying the SparseGPT pruning method. The results are shown for different numbers of iterations of the pruning algorithm, including the results for the dense (unpruned) models as a baseline. The table demonstrates how the accuracy changes as the number of iterations and model size change.

This table shows the perplexity scores achieved by three different methods on the WikiText2 and C4 datasets. The three methods are: Dense (the original, unpruned model), SparseGPT (a baseline one-shot pruning method), and I-OBS(3) (the proposed iterative method with 3 iterations). Lower perplexity indicates better performance.
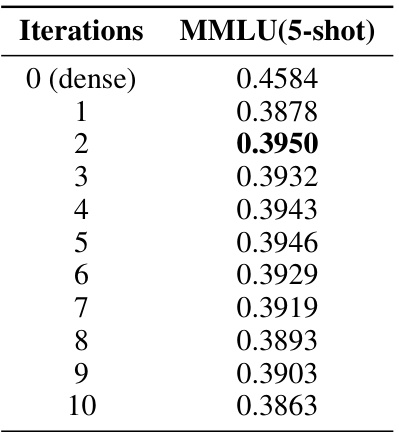
This table shows the performance of the Iterative Optimal Brain Surgeon (I-OBS) algorithm on the Llama-2-7B model for the MMLU (5-shot) task. The iterations column indicates the number of I-OBS iterations performed, starting from a dense model (iteration 0). The MMLU (5-shot) column shows the performance of the model on the MMLU benchmark after each I-OBS iteration. The best performance is highlighted in bold.
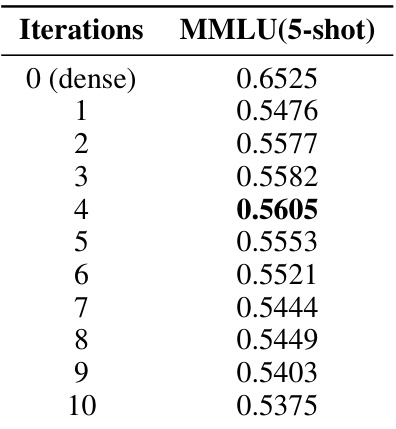
This table presents the performance of the Iterative Optimal Brain Surgeon (I-OBS) algorithm on the Llama-3-8B model, measured by the MMLU (5-shot) score. It shows the performance for various numbers of iterations, starting from the dense model (0 iterations). The MMLU score likely represents performance on the Multi-lingual Language Understanding Evaluation benchmark. The results highlight the I-OBS algorithm’s ability to improve model performance with each iteration, suggesting a trade-off between sparsity and performance.
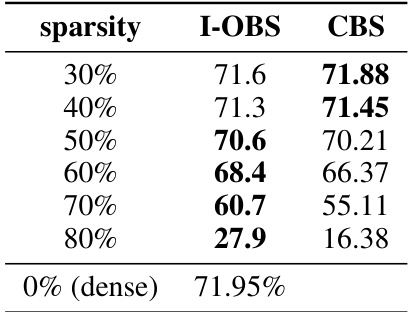
This table compares the performance of the proposed Iterative Optimal Brain Surgeon (I-OBS) algorithm with the Combinatorial Brain Surgeon (CBS) algorithm on the MobileNetV1 model. The comparison is made across various sparsity levels (30%, 40%, 50%, 60%, 70%, and 80%). The results show the accuracy obtained by each method at each sparsity level. The performance of the dense (0% sparsity) model is also provided as a baseline for comparison.
Full paper#