↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Ensemble sampling is a popular technique in reinforcement learning that balances exploration and exploitation by using an ensemble of models. Previous research on its theoretical performance in linear bandits—a simplified yet important model for sequential decision making—has been incomplete, with prior analyses either flawed or requiring unrealistic ensemble sizes. This hinders the practical adoption of ensemble sampling for complex tasks.
This paper addresses this by providing the first rigorous and useful analysis of ensemble sampling in the linear bandit setting. The authors prove that a much smaller ensemble (logarithmic in horizon size) is sufficient to achieve near-optimal performance. This work significantly advances our understanding of ensemble sampling and its potential applications, suggesting that it may be more practical for various learning tasks than previously thought. The findings are particularly valuable for high-dimensional problems, where linearly scaling ensembles would be computationally prohibitive.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides the first rigorous analysis of ensemble sampling for stochastic linear bandits, a widely used method in reinforcement learning. The findings challenge existing assumptions about the necessary ensemble size, opening new avenues for developing more efficient and scalable algorithms in various applications.
Visual Insights#
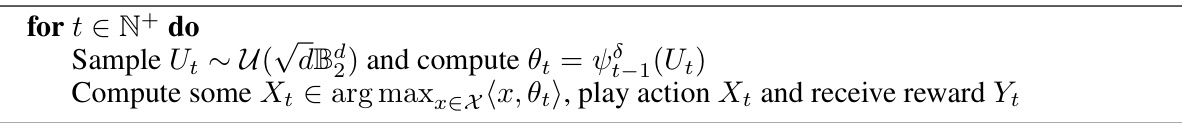
The algorithm outlines the steps involved in linear ensemble sampling. It starts by initializing parameters like regularization parameter, ensemble size, perturbation scales, and then iteratively computes and updates m+1 d-dimensional vectors. This includes a ridge regression estimate of theta* and m perturbation vectors, and selects an action that maximizes the predicted reward based on a randomly chosen perturbation. It updates the ensemble and repeats the process for each time step.
Full paper#



















