↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Subspace learning is crucial for analyzing high-dimensional data. Traditional methods often struggle with efficiency and robustness, particularly in online settings. This paper explores a novel approach using single-layer Generative Adversarial Networks (GANs), framing them as a new method for subspace learning. The core issue is that existing methods lack the ability to efficiently capture the underlying structure of high-dimensional data, especially when dealing with noisy or incomplete datasets.
The researchers analyze the training dynamics of single-layer GANs with a focus on the role of inter-feature interactions in multi-feature discriminators. Their analysis reveals that non-sequential learning (multi-feature) is superior to sequential learning (single-feature), leading to faster convergence and more accurate subspace representation. They confirm their findings through theoretical analysis and experiments using real-world datasets, demonstrating the effectiveness and robustness of the proposed multi-feature GAN approach for subspace learning tasks.
Key Takeaways#
Why does it matter?#
This paper is important because it offers new insights into the training dynamics of single-layer GANs, a fundamental model in machine learning. By bridging the analysis to subspace learning and introducing a multi-feature discriminator, it provides a more efficient and robust approach to this crucial task. This research also opens doors for further investigation into multi-layer GANs and the broader implications for high-dimensional data analysis.
Visual Insights#

This figure displays the results of Ordinary Differential Equation (ODE) simulations for various noise levels, comparing them to empirical simulations. Four noise levels (ης = ητ = 2, 1, 3, 4) are shown, illustrating the learning dynamics for a two-dimensional subspace (d=2) using a specific learning rate. The plot demonstrates the convergence of the model’s macroscopic state to values predicted by the ODE model, which suggests that the ODE accurately captures the essential dynamics of the generative adversarial network (GAN). Importantly, it’s noted that when the noise level (η) reaches 5 or above, the generator fails to learn effectively.
In-depth insights#
GAN Dynamics#
The analysis of GAN dynamics is crucial for understanding and improving GAN training. Understanding the dynamics allows researchers to diagnose training issues, such as mode collapse or vanishing gradients, and to develop better training strategies. The paper delves into the precise dynamics of single-layer GAN models through a rigorous scaling limit analysis. This theoretical approach provides insights into the behavior of the model and how features interact, especially with multi-feature discriminators. The focus on non-sequential feature learning offers a novel perspective compared to prior research that mainly investigated sequential learning. Theoretical analysis is supplemented by empirical validation on real-world datasets, showing that the theoretical insights translate to practical improvements. The study bridges GAN training with subspace learning, demonstrating the strengths of GANs in learning meaningful subspaces compared to other conventional methods. A key finding is the significant impact of multi-feature discriminators in accelerating learning and improving performance. This contributes to a richer understanding of GAN training and its potential applications in subspace learning tasks.
Multi-Feature Analysis#
A multi-feature analysis in the context of generative adversarial networks (GANs) would involve investigating how the model learns and interacts with multiple features simultaneously, rather than sequentially. The key is understanding the interplay and dependencies between features, which traditional single-feature analyses often overlook. This could reveal insights into how GANs achieve disentanglement or learn complex data representations. The analysis may involve comparing models trained with single-feature versus multi-feature discriminators to highlight the impact of simultaneous feature processing on training speed, convergence, and overall performance. Visualizing and analyzing how the generator modifies feature representations to match the true data distribution would also be a critical component. Furthermore, the analysis should examine the impact of this non-sequential processing on the GAN’s ability to generalize to unseen data, bridging the gap between theoretical analysis and practical application. A comparative analysis with conventional subspace learning methods would help establish the unique advantages of GAN-based multi-feature approaches.
ODE Framework#
The core of this research lies in its novel application of ordinary differential equation (ODE) frameworks to model and analyze the training dynamics of single-layer Generative Adversarial Networks (GANs). Instead of focusing solely on the discrete updates during GAN training, the authors leverage ODEs to capture the continuous-time evolution of the model’s parameters. This approach enables a deeper understanding of GAN behavior, particularly the complex interactions between the generator and discriminator. By analyzing the ODEs, they reveal key insights into the convergence properties and the role of various factors, such as learning rates and initialization strategies, in shaping the model’s performance. The use of ODEs allows for a more rigorous and mathematically tractable analysis of GAN training dynamics, moving beyond empirical observations to gain theoretical understanding. This framework is particularly valuable in uncovering how multi-feature discriminators impact training efficiency and the attainment of a more informative basis for the learned subspace. The resulting ODEs provide a concise yet powerful tool for evaluating and optimizing GAN architectures, offering a theoretical foundation for enhancing subspace learning in high-dimensional data.
Subspace Learning#
The concept of subspace learning, crucial in high-dimensional data analysis, is thoughtfully examined. The paper highlights its importance in handling modern datasets, where identifying meaningful subspaces within the data is paramount. Online methods, such as Oja’s method and GROUSE, are presented as efficient techniques for this task, particularly in high-dimensional settings. The paper then proposes a novel approach by framing single-layer Generative Adversarial Networks (GANs) as a method for subspace learning. This perspective provides a fresh lens for understanding GAN training dynamics, particularly through the investigation of multi-feature discriminators. A key insight is that inter-feature interactions within the discriminator are vital in accelerating training and improving performance, particularly when using an uninformed initialization strategy. The theoretical analysis, supported by both synthetic and real-world datasets (MNIST and Olivetti Faces), demonstrates the robustness of this GAN-based method in subspace learning and also unveils the unique ability of GANs to learn a more informative basis by generating new data samples. This is in contrast to conventional approaches which are shown to capture the subspace but with less efficiency and insight.
GAN Limitations#
Generative Adversarial Networks (GANs), while powerful, present significant limitations. Training instability is a major hurdle, with the generator and discriminator often falling into a cycle of poor performance. Mode collapse, where the generator produces limited variety, is another key issue. Evaluating GANs remains challenging; standard metrics often fail to capture the true quality of generated samples. The high computational cost of training GANs, particularly for high-resolution images, is a practical barrier. Hyperparameter sensitivity significantly impacts performance, requiring extensive experimentation. Lack of theoretical guarantees makes understanding and improving GAN training difficult. Finally, interpretability issues surrounding the learned representations hinder applications where understanding how the model generates images is vital. Addressing these limitations is key to unlocking GANs’ full potential.
More visual insights#
More on figures

This figure shows the results of simulations performed to validate the ODE model presented in the paper. It shows the cosine similarity over time for different noise levels (ης = ητ = 2, 1, 3, 4). The results indicate a good match between the simulations and the ODE model’s predictions. For noise levels above 4, the generator fails to learn, illustrating a limitation of the model.

This figure compares the performance of three subspace learning methods: Oja’s method, a multi-feature GAN, and a single-feature GAN, on the Olivetti Faces dataset. The y-axis represents the Grassmann distance between the learned subspace and the true subspace (approximated by full PCA). The x-axis shows the training time. The graph illustrates that the multi-feature GAN outperforms both Oja’s method and the single-feature GAN in terms of capturing the true data subspace, achieving a lower Grassmann distance.

This figure compares the top 16 learned features of three different subspace learning methods (GAN with multi-feature discriminator, GAN with single-feature discriminator, and Oja’s method) on the Olivetti Faces dataset at three different training stages (epoch 1, epoch 200, and final epoch). It demonstrates the qualitative difference in feature learning between the methods, highlighting the superior performance and diversity of features learned by the GAN with a multi-feature discriminator.

This figure compares the learned features of a multi-feature discriminator GAN model against a single-feature discriminator GAN model. Both models aim to learn 36 features from the MNIST dataset. The multi-feature model achieves good results in a single epoch, whereas the single-feature model requires 5 epochs to reach a similar level of performance. The visualization shows that the multi-feature model learns clear and recognizable features, while the single-feature model produces many noisy or unclear features.

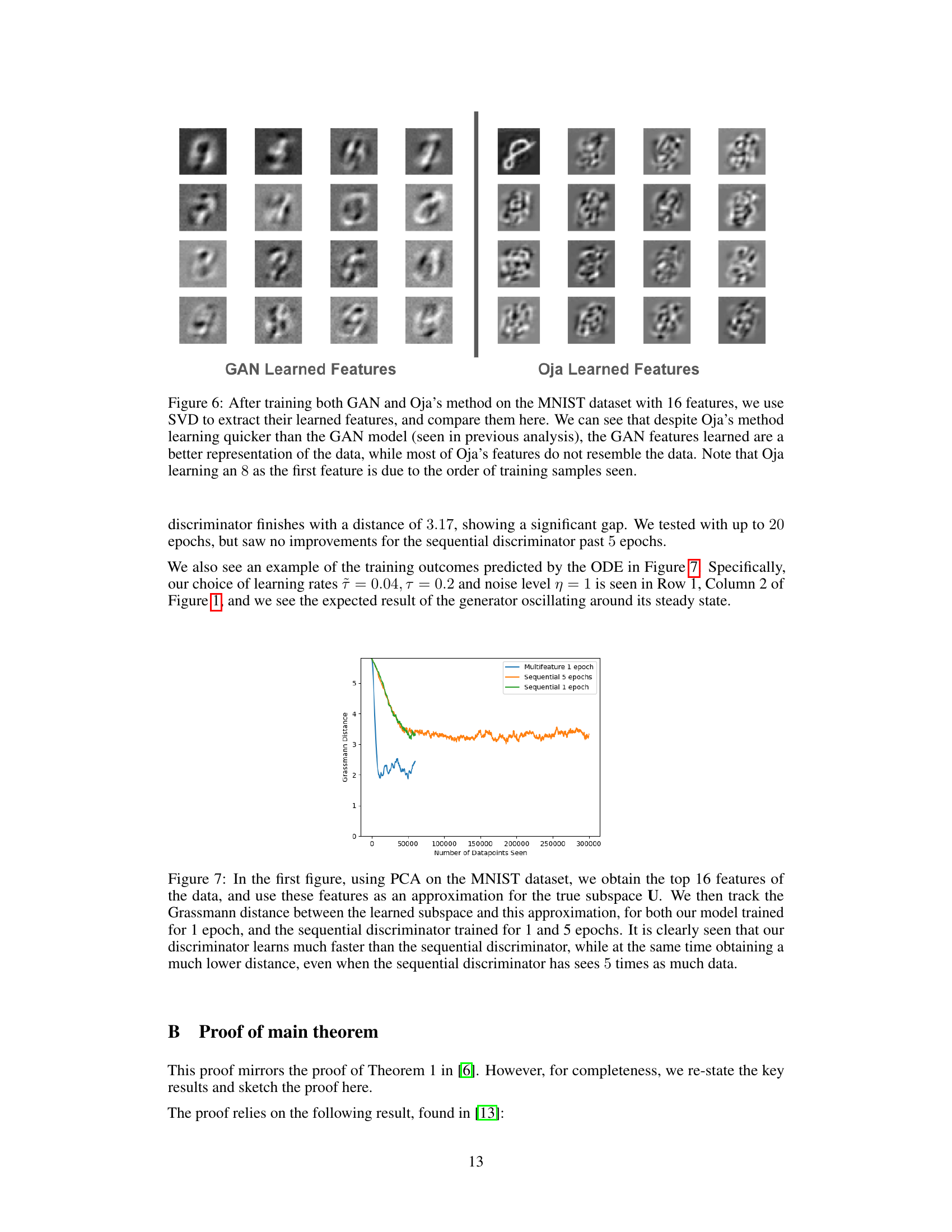
This figure compares the features learned by GAN and Oja’s method on the MNIST dataset. The left side shows the top 16 features learned by the GAN model, while the right shows those learned by Oja’s method. Each image represents a single feature vector. The caption highlights that GAN learns features that better represent the dataset despite Oja’s method being faster. The order of features learned by Oja’s method is influenced by the order of training samples.

This figure compares the Grassmann distances for the multi-feature and single-feature discriminators. The Grassmann distance measures the similarity between two subspaces. The results show that the multi-feature discriminator learns a subspace that is much closer to the true subspace (as determined by PCA) than the single-feature discriminator, even when the single-feature discriminator is trained for five times as many epochs (iterations).
Full paper#