↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional methods for modeling disease progression struggle with high-dimensionality and computational cost, limiting their ability to incorporate rich clinical data like images. This makes it difficult to achieve detailed, pixel-level understanding of disease mechanisms.
This research proposes a novel method called the variational event-based model (vEBM), leveraging optimal transport to overcome these issues. The vEBM drastically speeds up the inference process, making it computationally feasible to model high-dimensional data. It allows for pixel-level disease progression analysis, offering a new level of granularity and interpretability. The results on both synthetic and real-world data demonstrated the improved speed and accuracy, showcasing the vEBM’s potential for transforming disease research.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers studying disease progression because it introduces a novel method that significantly speeds up inference and enables high-dimensional modeling. This addresses a major limitation in the field, opening avenues for more detailed and accurate modeling of complex diseases using diverse data types.
Visual Insights#

This figure schematically describes the variational event-based model (vEBM) using a toy dataset with four features. Panel A shows the input data as snapshots from multiple individuals, with each feature potentially exhibiting abnormality or normality. Panel B illustrates the inference process, where probabilistic models of normality and abnormality are first fit to the data. The core of the inference uses the Sinkhorn-Knopp algorithm to optimize the Evidence Lower Bound (ELBO) and iteratively update the permutation matrix (S). Panel C demonstrates how the hard permutation (s), representing the disease event sequence, is derived from the inferred permutation matrix S. The key point is that the vEBM’s permutation matrix S is a probability distribution that can be sampled to quantify uncertainty.

This table presents the results of a hyperparameter study on the temperature parameter (τ) in the variational event-based model (vEBM). It shows the Kendall’s tau correlation and the fraction of correctly inferred events for different values of τ (0.1 and 10.0) and for three different model sizes (100x10, 1000x100, 2000x200 features). The results are based on synthetic data with noise (σ = 0.5). The purpose is to illustrate how the choice of τ impacts model performance.
In-depth insights#
Optimal Transport#
The concept of Optimal Transport (OT) is ingeniously leveraged in this research to address the computational challenges inherent in modeling disease progression. Traditional methods struggle with the combinatorial explosion of possibilities when dealing with high-dimensional data representing multiple disease events. OT elegantly recasts the problem as one of finding the optimal ’transport plan’ to map observed data to latent disease event sequences. This reformulation bypasses the combinatorial hurdles and facilitates efficient inference. The authors employ an entropy-regularized OT approach, employing the Sinkhorn-Knopp algorithm, enhancing computational tractability. This framework allows for the analysis of significantly larger datasets and more complex models than previously feasible, ultimately leading to improved speed and accuracy in uncovering disease progression patterns. The transition to a continuous latent permutation matrix within the Birkhoff polytope is a key innovation, enabling fast inference through variational lower bound optimization. This innovative application of OT marks a substantial advance in the field, pushing the boundaries of what’s computationally possible in disease progression modeling.
Variational Inference#
Variational inference, a core methodology in the paper, offers a powerful technique for approximating intractable posterior distributions. By introducing a tractable variational distribution, it enables efficient estimation of model parameters. The choice of variational family significantly impacts the accuracy and computational cost. The paper highlights the use of the Gumbel-Sinkhorn distribution for its unique ability to model latent permutations, resulting in enhanced efficiency and interpretability. A key contribution is leveraging this distribution to achieve fast inference in high-dimensional models, previously computationally prohibitive. The effectiveness of the variational approach is carefully demonstrated, particularly in the context of high-dimensional disease progression modeling. The algorithm’s performance, even with noise, underscores the robustness of this approach. However, the limitations of the variational approximation, potentially resulting in biased estimates, warrant consideration. Overall, variational inference is shown as a critical component enabling scalability and efficiency, leading to novel analyses not previously feasible.
Pixel-level Progression#
The concept of “Pixel-level Progression” represents a significant advancement in disease modeling. By analyzing changes at the individual pixel level in medical images (like MRI or OCT scans), researchers can move beyond broad, regional assessments of disease and gain finer-grained insights into the spatiotemporal dynamics of the condition. This approach offers enhanced precision in tracking disease onset, progression, and even subtle changes often missed by conventional methods. It allows for the identification of early disease markers, provides a more accurate representation of disease heterogeneity, and facilitates individualized patient monitoring. However, this granularity necessitates computational efficiency and robust handling of high-dimensional data, as well as addressing the potential noise inherent in medical images. Success in this area relies on computationally efficient algorithms and innovative approaches to visualize the progression over time, which can prove particularly impactful for diseases that affect multiple tissue types or are characterized by highly variable presentations.
Computational Speed#
The research paper significantly emphasizes computational speed as a critical factor influencing the practicality and scalability of disease progression models. Traditional maximum likelihood approaches for discrete models face challenges due to combinatorial explosion, limiting model dimensionality and hindering their applicability to large datasets. The paper addresses this limitation by leveraging optimal transport theory, which enables faster inference of event permutations. This novel method, named the variational event-based model (vEBM), is shown to achieve a 1000x speedup compared to existing state-of-the-art methods. This substantial improvement is critical for handling high-dimensional data, such as pixel-level information from medical images, enabling detailed analyses not previously feasible. The enhanced speed supports models with orders of magnitude more features, increasing the accuracy and robustness of results, all while maintaining model interpretability. Computational efficiency is presented as a key contribution, broadening the application of these models to diverse datasets and clinical scenarios.
Future Directions#
Future directions for this research could involve exploring more complex data modalities beyond imaging and clinical scores, such as genomics and proteomics. Integrating these diverse data types could provide a more holistic understanding of disease progression and identify novel biomarkers. Another area of exploration is improving model interpretability. While the current model offers insights into pixel-level events, further advancements in visualization techniques could enhance the understanding of disease mechanisms. Developing more robust inference methods to handle missing data and noise is also crucial. Investigating the vEBM’s ability to handle non-monotonic disease progression would enhance its applicability to a wider range of conditions. Finally, extending the model to accommodate multiple disease subtypes within a single dataset would further refine the model’s clinical utility and ability to deliver personalized medicine.
More visual insights#
More on figures

This figure compares the runtime performance of three different models (vEBM, EBM, and ALPACA) for disease progression inference across various numbers of features. The x-axis represents the number of features in the dataset, while the y-axis shows the wall-clock time in seconds. The vEBM consistently demonstrates significantly faster inference times compared to the other two models, showcasing its scalability to high-dimensional datasets. The ALPACA model becomes computationally intractable for larger numbers of features (J=200), illustrating the vEBM’s advantage in handling complex datasets.

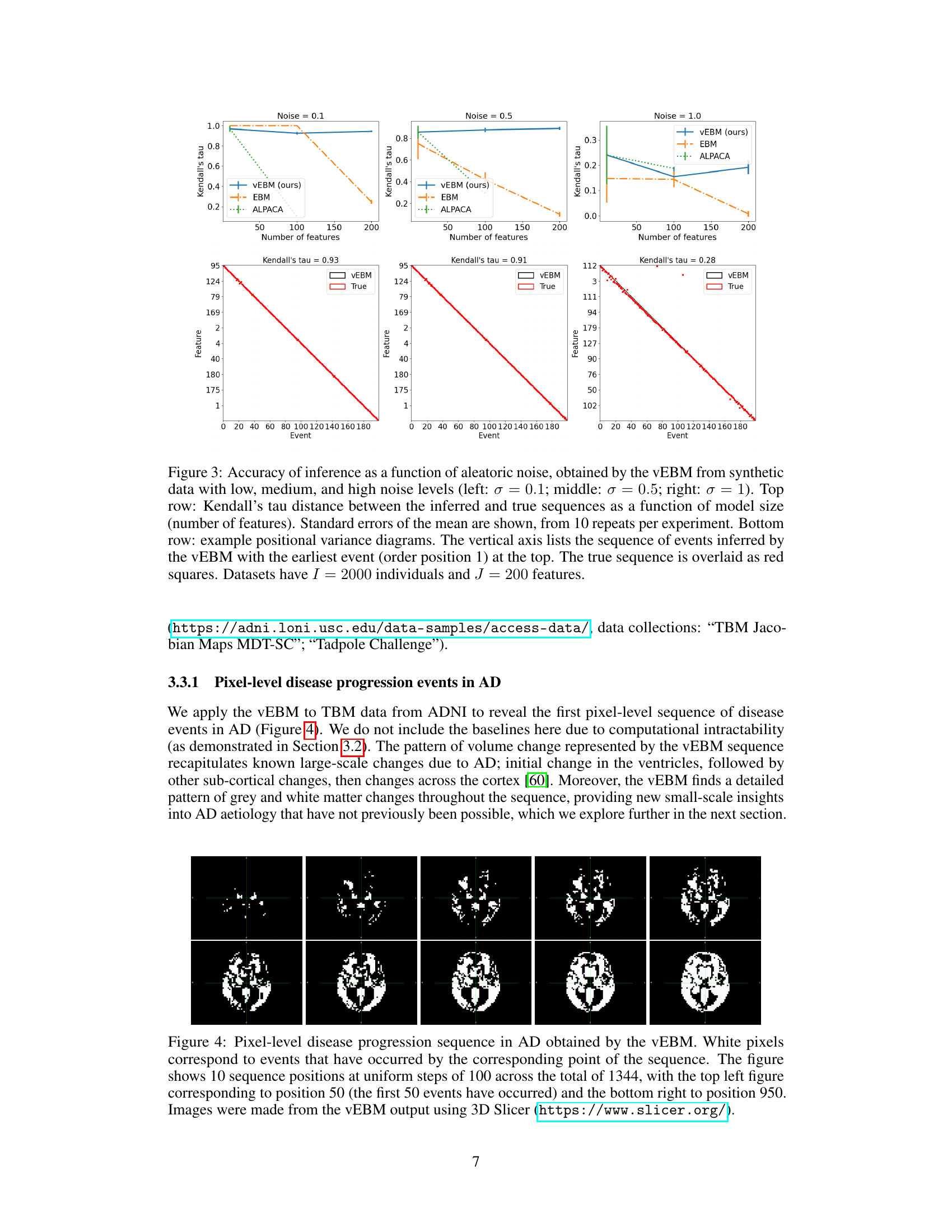
This figure demonstrates the accuracy and robustness of the variational event-based model (vEBM) against increasing noise levels in synthetic datasets. The top row shows Kendall’s tau, a measure of rank correlation, indicating the similarity between the inferred and true event sequences. The bottom row provides positional variance diagrams, visualizing the alignment of inferred and true event orders for different features, highlighting the model’s performance across various noise levels.

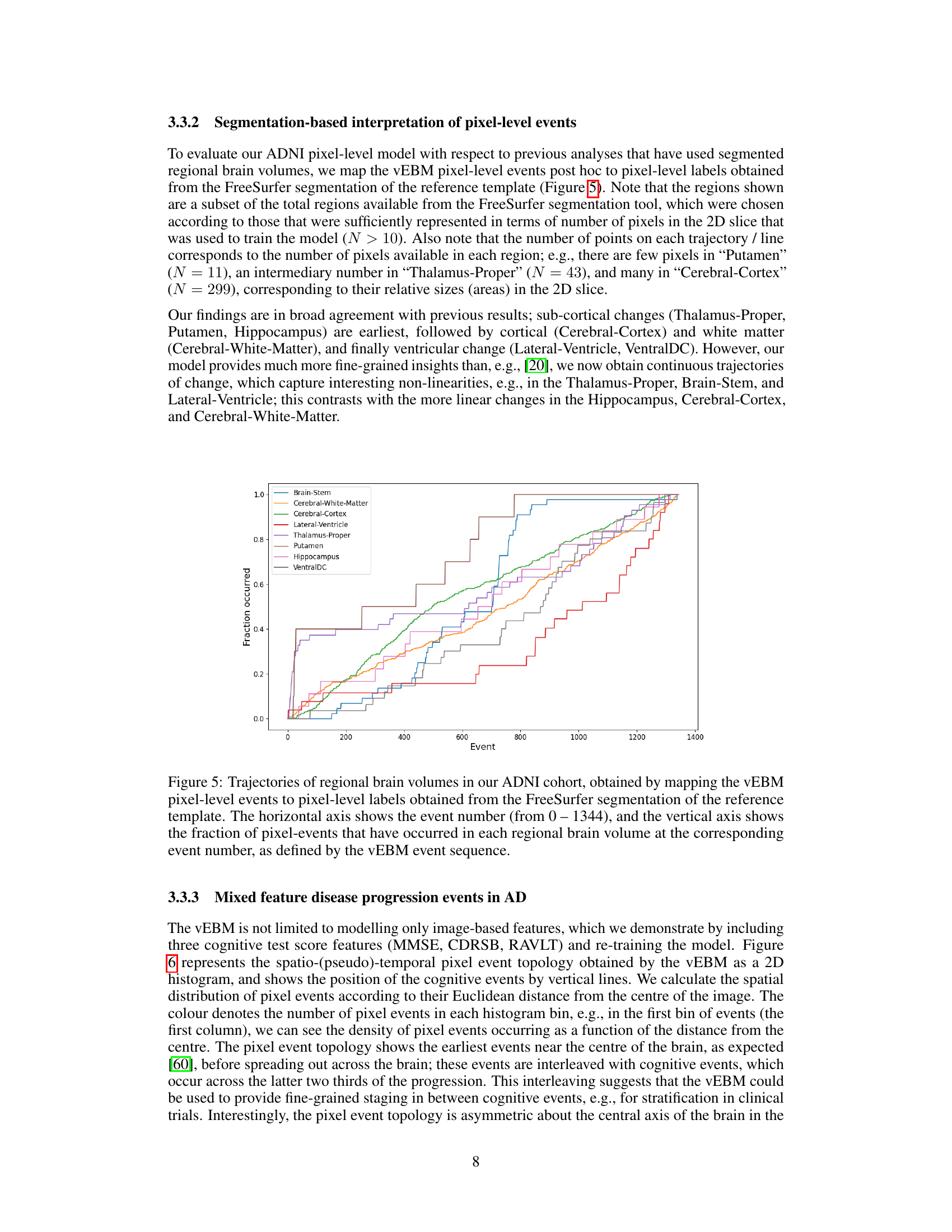
This figure shows the progression of Alzheimer’s Disease at the pixel level, obtained by applying the variational event-based model (vEBM) to tensor-based morphometry (TBM) data. Each image represents a snapshot of the brain at a specific point in the progression sequence. White pixels indicate brain regions where a disease event has occurred. The sequence of images illustrates the spread of the disease across the brain over time, starting in the ventricles and progressing to the cortex.

This figure shows the trajectories of regional brain volumes over the course of Alzheimer’s disease progression. The x-axis represents the event number (from a total of 1344 events identified by the model) and the y-axis shows the fraction of pixel-level events that have occurred in each region. The data comes from the ADNI study, and the regions were defined using FreeSurfer segmentation. The plot allows visualization of the temporal order in which different brain regions show signs of disease progression.
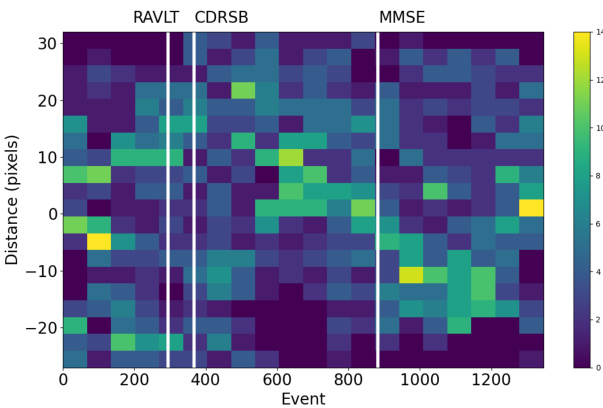
This figure shows a 2D histogram representing the spatio-temporal distribution of pixel events (horizontal axis) and their distance from the brain’s center (vertical axis), as determined by the vEBM model for Alzheimer’s disease. The vertical lines indicate the positions of cognitive events within the progression sequence. The color intensity corresponds to the density of pixel events at each location in the space. The asymmetry around the central axis suggests potential variations in the disease progression pattern across the brain.

This figure shows the pixel-level disease progression sequence in Alzheimer’s disease (AD) obtained using the variational event-based model (vEBM). It visualizes the progression of the disease spatially across the brain over time, showing which pixels have become abnormal (white) at each stage of the progression. The images represent ten snapshots of the process, each showing the cumulative number of events that have occurred up to that point in time. The figure shows how the disease progresses, starting in certain regions and spreading throughout the brain.
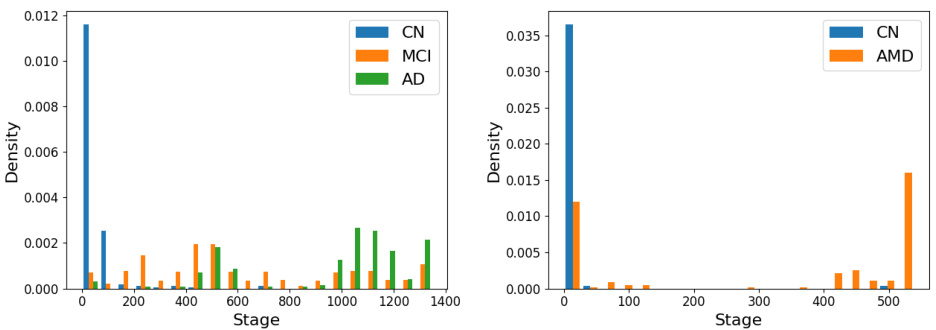
This figure shows the distribution of individual-level stages obtained by the variational event-based model (vEBM) in Alzheimer’s disease (AD) and age-related macular degeneration (AMD). The left panel displays the stage distribution for AD, categorizing individuals into control (CN), mild cognitive impairment (MCI), and AD groups. The right panel shows the stage distribution for AMD, with control (CN) and AMD groups. The x-axis represents the stage (an integer value indicating the progression of the disease), and the y-axis represents the density of individuals at each stage. The distributions show how well the vEBM is able to stratify individuals according to their disease stage, highlighting its potential for use in clinical trials and other applications that require accurate staging.

This figure shows the graphical model for the variational event-based model. The model has latent variables (circles) and observed variables (squares). The latent variables include the event permutation matrix (S), the initial probability vector (π), and the disease state for each individual (ki). The observed variables are the biomarker data (Yi,j). The arrows indicate the dependencies between variables. This model uses a hierarchical Bayesian approach, where the observed data depend on the latent states and the model parameters.
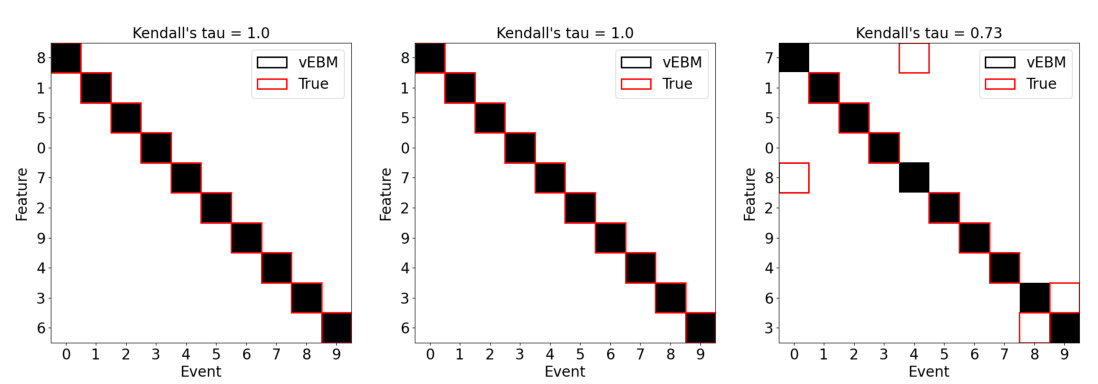
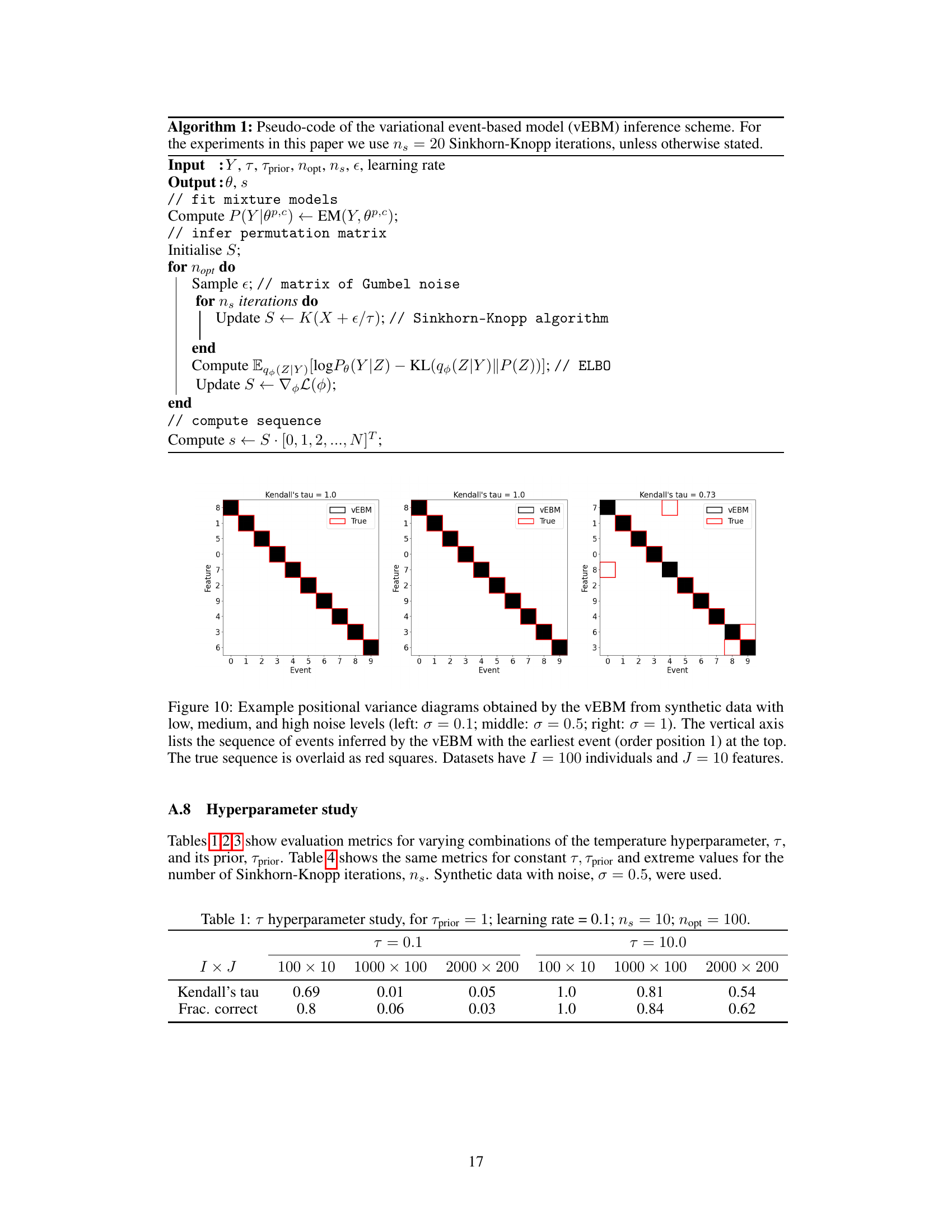
This figure shows positional variance diagrams for three different noise levels (low, medium, and high). Each diagram displays the sequence of events inferred by the vEBM, compared to the true event sequence, with the earliest event at the top. The vertical axis represents the sequence of events, while the horizontal axis represents the feature index. The red squares show the true order of events. The degree of variation from the true order (uncertainty) is shown visually. Datasets used for this example have 100 individuals and 10 features.
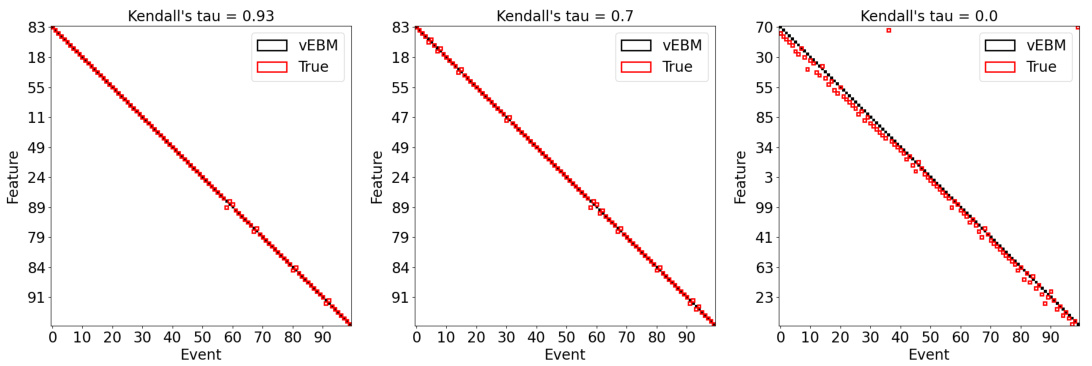
This figure demonstrates the accuracy and robustness of the variational event-based model (vEBM) against varying levels of noise in synthetic datasets. The top row shows the Kendall’s tau correlation between the true and inferred event sequences at different model sizes (number of features) and noise levels (σ = 0.1, 0.5, 1). The bottom row provides example positional variance diagrams that visualize the inferred event order against the true order, showcasing the VEMB’s ability to maintain accuracy even with significant noise.
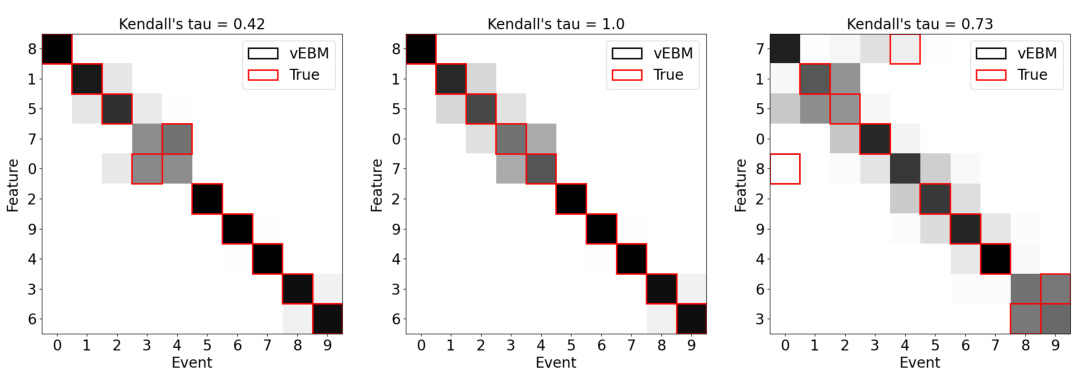
This figure demonstrates the performance of the variational event-based model (vEBM) in handling different levels of noise. The top row shows that the VEMB consistently outperforms or matches other methods in terms of Kendall’s tau, which measures the correlation between the true and inferred event sequences. The bottom row shows positional variance diagrams, which visually represent the consistency of the VEMB’s performance across various levels of noise.

This figure demonstrates the performance of the variational event-based model (vEBM) in handling varying levels of noise in synthetic data. The top row shows that the vEBM maintains high accuracy even with increasing noise levels, indicated by Kendall’s tau values, in datasets with 2000 individuals and 200 features. The bottom row shows example positional variance diagrams, illustrating the relationship between the inferred and true event sequences.

This figure demonstrates the accuracy and robustness of the variational event-based model (vEBM) against increasing noise levels in synthetic data. The top row shows Kendall’s tau, a measure of rank correlation between the inferred and true event sequences, plotted against the number of features for different noise levels (σ = 0.1, 0.5, 1). The bottom row provides example positional variance diagrams illustrating the inferred event sequence compared to the true sequence for each noise level. The diagrams visually represent the model’s ability to accurately infer the event order despite noise.
More on tables

This table presents the results of a hyperparameter study focusing on the temperature parameter (τ) in the vEBM model. It shows the Kendall’s tau correlation and the fraction of correctly inferred sequences for different model sizes (100x10, 1000x100, and 2000x200 features) and two values of τ (0.1 and 10.0). The results demonstrate how the performance of the model varies with different temperature parameters and model complexities.

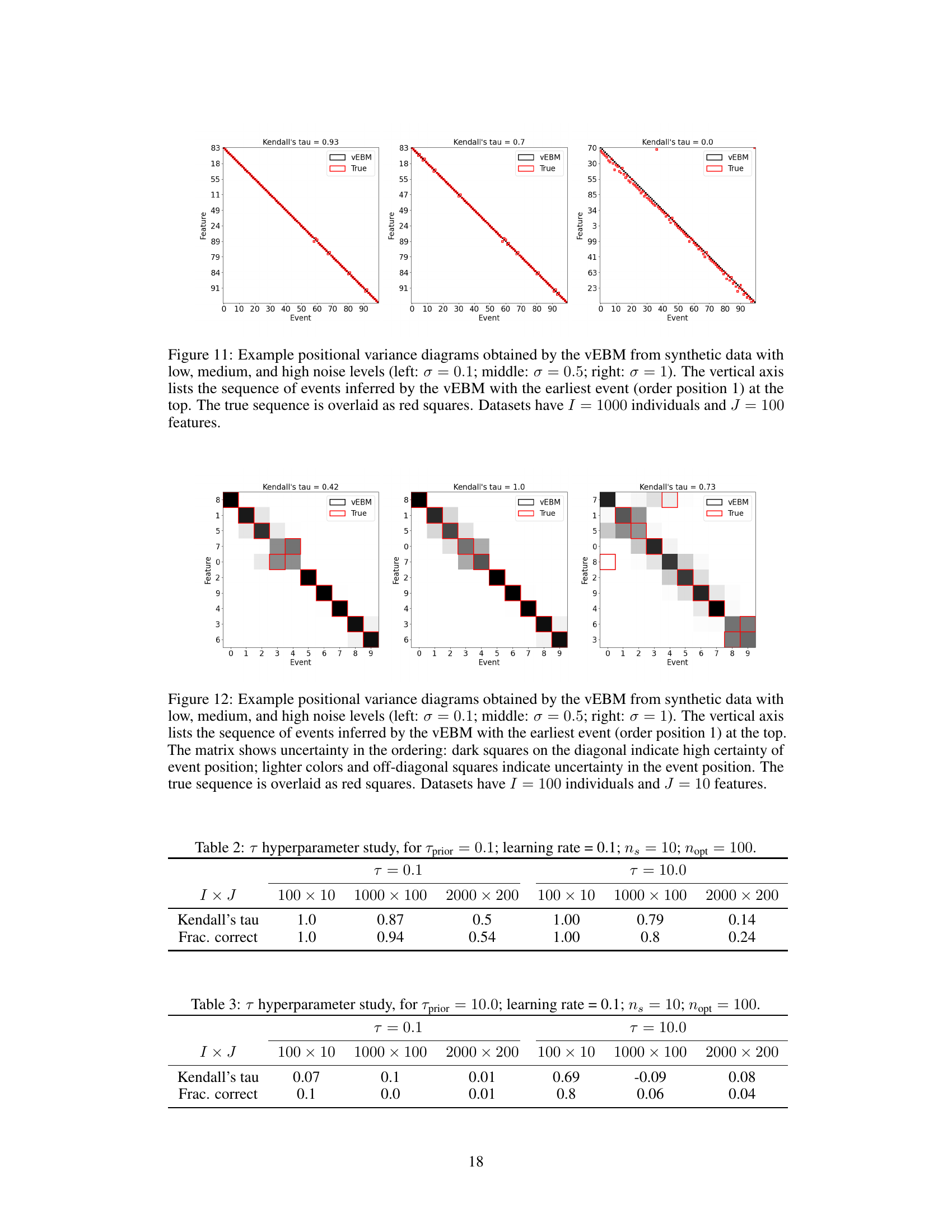
This table presents the results of a hyperparameter study focusing on the temperature parameter (τ) within the variational event-based model (vEBM). It shows the Kendall’s tau correlation and fraction of correctly inferred sequences for different dataset sizes (I x J) and two values of τ (0.1 and 10.0). The results illustrate the model’s sensitivity to the choice of τ and dataset size, with varying performance observed across different conditions.

This table presents the result of a hyperparameter study focusing on the number of Sinkhorn-Knopp iterations (ns) in the vEBM model. It shows the Kendall’s tau correlation and fraction of correctly inferred sequences for different model sizes (I x J) and two values of ns: 1 and 100. The results demonstrate the impact of this hyperparameter on the accuracy of the model’s inference.
Full paper#