↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current graph anomaly detection methods typically focus on a single graph object type (node, edge, or graph), overlooking the relationships between different types of anomalies. This can lead to inaccurate and incomplete detection, particularly in complex scenarios where different levels of anomalies are interconnected. For example, a money laundering transaction might involve an abnormal account (node-level anomaly) and unusual communication patterns (edge-level anomaly) within a specific community (graph-level anomaly).
UniGAD tackles this problem by providing a unified framework to detect node, edge, and graph-level anomalies jointly. It introduces the MRQSampler, a novel subgraph sampling technique that preserves significant anomaly information across different levels, and the GraphStitch Network, which effectively integrates and balances multi-level training. Experiments demonstrate that UniGAD outperforms existing methods specialized for single-level tasks and also achieves robust zero-shot task transferability, highlighting its versatility and effectiveness in various real-world applications.
Key Takeaways#
Why does it matter?#
This paper is important because it presents UniGAD, the first unified framework for graph anomaly detection across multiple levels (node, edge, graph). This addresses a critical limitation in existing methods, which often focus on a single level. The unified approach improves accuracy, robustness, and transferability, opening avenues for more effective anomaly detection in various domains. Its novel subgraph sampling technique and multi-level training strategy are valuable contributions to the field.
Visual Insights#
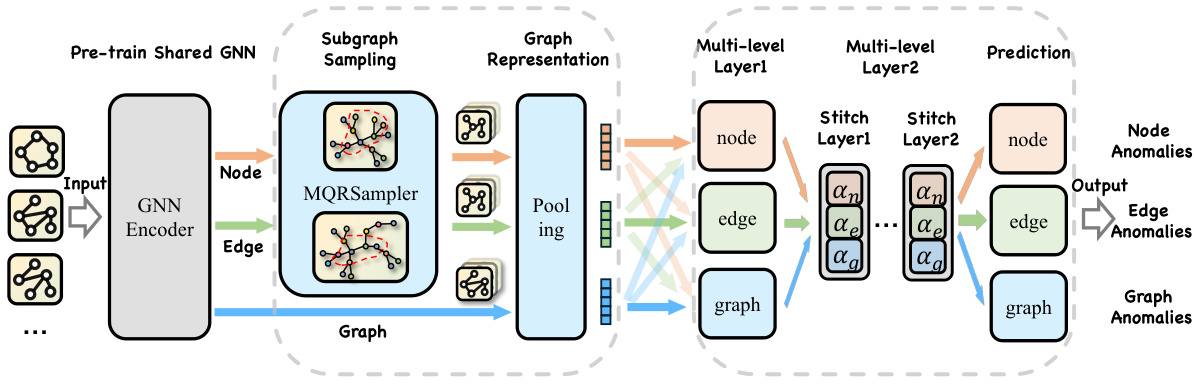
The figure illustrates the architecture of UniGAD, a unified graph anomaly detection model. It shows a series of processing steps: First, a pre-trained shared Graph Neural Network (GNN) encoder processes the input data (nodes, edges, and graphs). Next, a Maximum Rayleigh Quotient Subgraph Sampler (MRQSampler) samples subgraphs to unify multi-level formats. Then, pooling layers create graph representations. These representations are then processed by a multi-level layer (Layer1 and Layer2). A GraphStitch Network combines the outputs from these layers, unifying multi-level training. Finally, multi-level prediction layers produce the anomaly predictions for nodes, edges, and graphs.
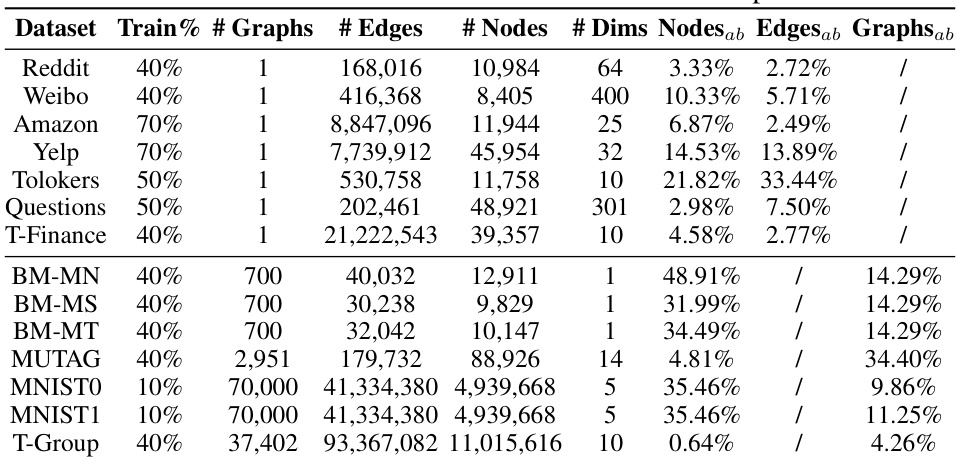
This table presents a detailed overview of the fourteen datasets employed in the UniGAD experiments. For each dataset, it lists the percentage of data used for training, the number of graphs, the number of edges, the number of nodes, the feature dimensionality, and the percentage of abnormal nodes, edges, and graphs.
In-depth insights#
Multi-level GAD#
Multi-level Graph Anomaly Detection (GAD) tackles the challenge of identifying anomalies across various granularities within graph data, moving beyond the traditional node- or edge-level focus. This multi-level approach is crucial because anomalies often manifest as interconnected patterns involving nodes, edges, and entire subgraphs. UniGAD, for instance, directly addresses this by jointly detecting anomalies at all three levels, recognizing the complex relationships between them. A key advantage of multi-level GAD is its ability to capture a holistic view of anomalies, providing a richer and more informative understanding than single-level methods. The unified approach improves accuracy and robustness, as it leverages the complementary information available at each level. However, this complexity introduces new challenges, such as the need for effective information integration and harmonization of potentially conflicting training objectives. UniGAD’s approach employs a novel subgraph sampler and a GraphStitch Network to overcome this, showcasing a successful framework for multi-level GAD. The method also emphasizes the potential for zero-shot transferability, further enhancing its efficiency and adaptability. Future research should explore more sophisticated multi-level architectures and advanced strategies for handling diverse anomaly types and imbalanced datasets within this framework.
Unified Framework#
A unified framework in a research paper typically aims to integrate multiple methods or models to address a complex problem holistically. Instead of tackling individual components separately, a unified approach seeks to leverage the interdependencies and synergies between them. This often results in a more robust, efficient, and effective solution than using individual methods in isolation. For example, in graph anomaly detection, a unified framework might combine node-level, edge-level, and graph-level anomaly detection techniques, recognizing that anomalies at one level often influence other levels. Such an approach would likely involve novel ways to represent data, transfer information between levels, and harmonize training objectives. The success of a unified framework depends critically on its ability to effectively manage complexity, avoid conflicting goals, and ensure generalizability. Furthermore, a well-designed unified framework should provide improved performance and robustness compared to existing methods while also offering insights into the underlying problem structure. A key benefit is usually better zero-shot task transferability, meaning the unified model can handle new tasks or variations without needing retraining.
Spectral Subgraph#
The concept of “Spectral Subgraph” merges spectral graph theory with subgraph analysis. It suggests leveraging the eigenvalues and eigenvectors of a graph’s Laplacian matrix (or similar spectral representation) to guide the selection or construction of meaningful subgraphs. This approach is powerful because spectral properties often reflect global structural information and community patterns, which are crucial for many graph applications. Anomalous subgraphs, for instance, might exhibit unusual spectral signatures, enabling their identification. Efficiently computing spectral properties for large graphs is crucial, often involving approximation techniques. Furthermore, choosing the appropriate spectral measure (e.g., eigenvalues, eigenvectors, or other spectral features) is critical, depending on the task. Defining how to translate global spectral information into local subgraph structures remains a key challenge. Combining spectral methods with efficient subgraph sampling strategies will be vital for scalability and practical application.
GraphStitch Network#
The proposed GraphStitch Network ingeniously addresses the challenge of unifying multi-level training in graph anomaly detection. Instead of a single, monolithic model, UniGAD leverages separate-but-identical networks for node, edge, and graph levels, recognizing the inherent differences in anomaly representation at each level. These specialized networks are then elegantly stitched together via a GraphStitch Unit, enabling controlled information sharing across levels. This approach avoids the pitfalls of forcing disparate tasks into a single architecture, mitigating negative interactions between gradients and preventing a single level from dominating the training process. The result is a harmonious training strategy that leverages the strengths of each level, while maintaining their individual efficacy, ultimately improving the model’s robustness and overall performance. The theoretical underpinnings of the GraphStitch unit and its ability to efficiently distribute the weight of gradient information across levels represents a key innovation and a significant contribution to multi-task graph learning.
Zero-shot Transfer#
Zero-shot transfer learning in the context of graph anomaly detection is a significant advancement. It implies a model’s ability to detect anomalies in unseen tasks or graph types without any explicit training on those specific tasks. This capability is crucial for real-world applications due to the ever-evolving nature of graph data and the scarcity of labeled data across diverse tasks. The success of zero-shot transfer relies on the model’s ability to leverage learned representations and relationships from previously seen tasks to generalize to new ones. This often involves using a shared feature extractor or a robust, generalizable architecture that can adapt to new input data. Transferability is particularly beneficial when dealing with limited or imbalanced datasets, enabling efficient anomaly detection across multiple tasks with reduced labeling efforts. However, the effectiveness of zero-shot transfer is highly dependent on the similarity between the source and target tasks. A model trained on highly specialized graph structures may not generalize well to different graph types. Addressing this limitation is key to enhancing the practical value of zero-shot transfer approaches in graph anomaly detection.
More visual insights#
More on figures
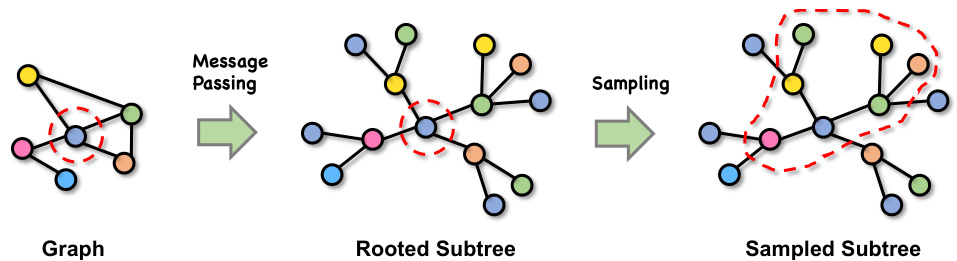
This figure illustrates the subgraph sampling process used in the UniGAD model. It shows three stages: 1) The original graph with a node highlighted (target node). 2) The rooted subtree centered on that target node after the message-passing phase of a Graph Neural Network (GNN). The subtree contains the information directly obtained from the target node and its immediate neighbors. 3) A sampled subtree, which is a subset of the rooted subtree. The red dashed line highlights that the sampled subtree is a smaller portion of the rooted subtree, chosen by an algorithm to best retain the most significant anomaly information.

The figure illustrates the MRQSampler algorithm’s operation. The algorithm recursively decomposes the problem of finding the optimal subtree into smaller subproblems by exploring the tree’s depth. Each smaller problem involves identifying the optimal nodeset for a subtree, maximizing the accumulated spectral energy. The process combines dynamic programming for efficiency and theoretical guarantees ensuring the most significant anomaly information is retained in the final subgraph.

The figure illustrates the architecture of the GraphStitch network, a key component of UniGAD. It shows how separate but identical networks for nodes, edges, and graphs are integrated using GraphStitch Units. The GraphStitch Units facilitate information sharing across different levels (node, edge, and graph) to unify multi-level training. The figure highlights the node level for clarity, showing how node embeddings are composed of information from node, edge, and graph perspectives.
This figure presents a detailed overview of the UniGAD framework. It illustrates the different stages involved in the process, starting from pre-trained shared GNN to the multi-level prediction. UniGAD unifies multi-level formats by transferring node, edge, and graph-level tasks into graph-level tasks on subgraphs (using MRQSampler), and unifies multi-level training by integrating information across different levels (using GraphStitch Network). The figure highlights the key components of UniGAD, including the pre-trained shared GNN, subgraph sampling, multi-level layers, and finally the multi-level prediction. The components of multi-level prediction are clearly shown: node anomaly detection, edge anomaly detection, and graph anomaly detection.
More on tables

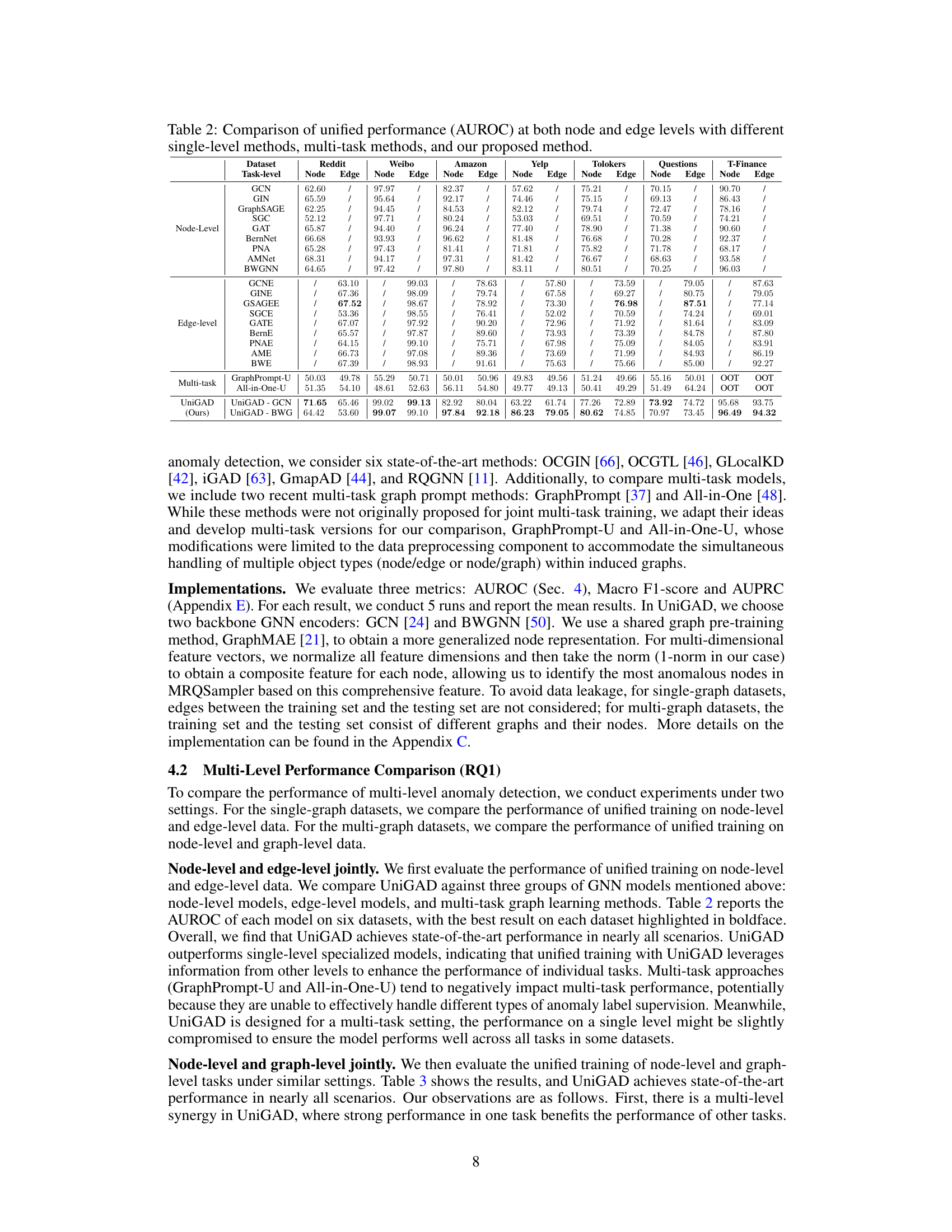
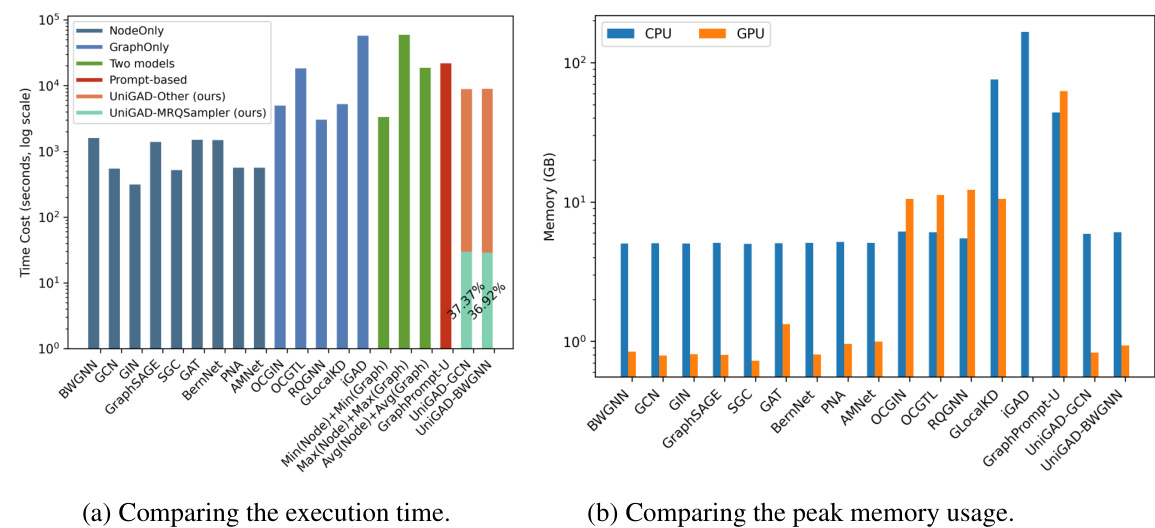
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) results for node-level and edge-level anomaly detection tasks. It compares the performance of UniGAD against various single-level methods (specialized for node or edge level tasks), and multi-task methods. The table highlights the superior performance of UniGAD in unifying multi-level anomaly detection by showing its AUROC scores across different datasets. Note that some multi-task baselines show ‘OOT’ (out of time) results, indicating limitations in their scalability.
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) for node-level and edge-level anomaly detection tasks. It compares the performance of UniGAD against various single-level methods (specialized for either node or edge-level tasks), multi-task learning methods, and a baseline GCN model. The results show UniGAD’s effectiveness in unifying multi-level tasks and improving performance over existing state-of-the-art methods.

This table compares the Area Under the Receiver Operating Characteristic curve (AUROC) scores for different graph anomaly detection methods on various datasets. It contrasts the performance of UniGAD against single-level methods focused solely on node or edge anomaly detection, as well as multi-task methods that attempt to handle both levels simultaneously. The results illustrate the effectiveness of UniGAD’s unified approach in achieving superior performance across different datasets and tasks compared to more specialized methods.
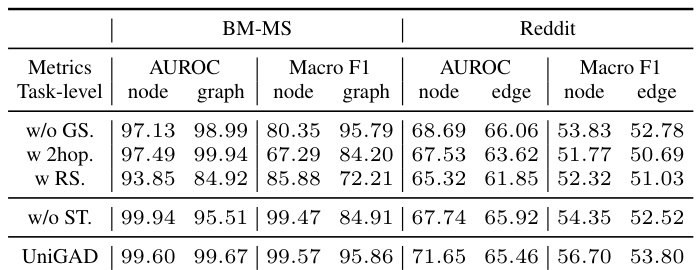
This table presents the ablation study results for UniGAD, showing the impact of different model components. It compares the performance of UniGAD against three variants: one without the subgraph sampler (w/o GS), one using a simpler 2-hop subgraph sampler (w 2hop), one using random sampling (w RS), and one without the GraphStitch Network (w/o ST). The results demonstrate the contributions of the subgraph sampler and GraphStitch Network to the overall performance of UniGAD.

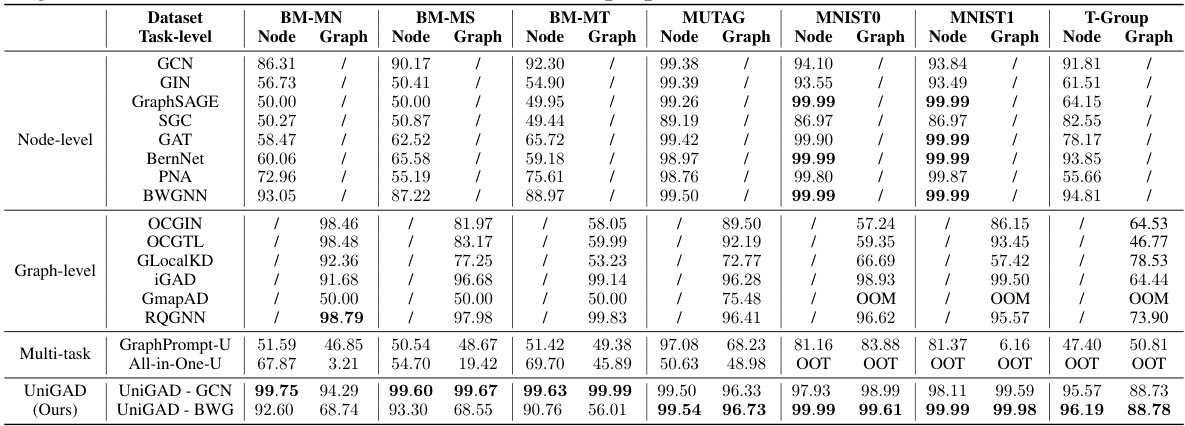
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) scores for various graph anomaly detection methods on seven datasets. It compares the performance of UniGAD against single-level methods (node-level and graph-level), multi-task methods, and UniGAD with different backbone GNNs (GCN and BWGNN). The table shows the AUROC for node-level and graph-level tasks separately for each method and dataset, allowing for a comprehensive performance comparison across different model types and datasets. The results demonstrate UniGAD’s ability to effectively unify multi-level anomaly detection, surpassing the performance of single-task and traditional multi-task approaches.
This table shows the hyperparameter search space used for training the UniGAD model. It lists each hyperparameter (learning rate, activation function, hidden dimension, MRQSampler tree depth, GraphStitch Network layer, and epochs) along with the range of values explored during the hyperparameter search.

This table presents the Area Under the Receiver Operating Characteristic Curve (AUROC) scores for various anomaly detection methods on six datasets. It compares the performance of UniGAD, a unified multi-level approach, against single-level methods (node-level and edge-level) and multi-task methods. The results show how well each method identifies anomalies at both the node and edge levels in a graph. UniGAD aims to outperform other methods by jointly considering information from both levels.

This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) for node-level and edge-level anomaly detection across six datasets. It compares the performance of UniGAD against various single-task methods (GCN, GIN, GraphSAGE, etc.), edge-level methods (GCNE, GINE, etc.), and multi-task methods (GraphPrompt-U, All-in-One-U). The results highlight UniGAD’s superior performance in unifying multi-level anomaly detection.

This table presents the Area Under the Receiver Operating Characteristic Curve (AUROC) scores for node-level and edge-level anomaly detection using various methods. It compares the performance of UniGAD against several single-level (node-only or edge-only) methods, as well as multi-task learning methods. The results show UniGAD’s ability to perform well across different datasets and task types, often outperforming specialized methods.

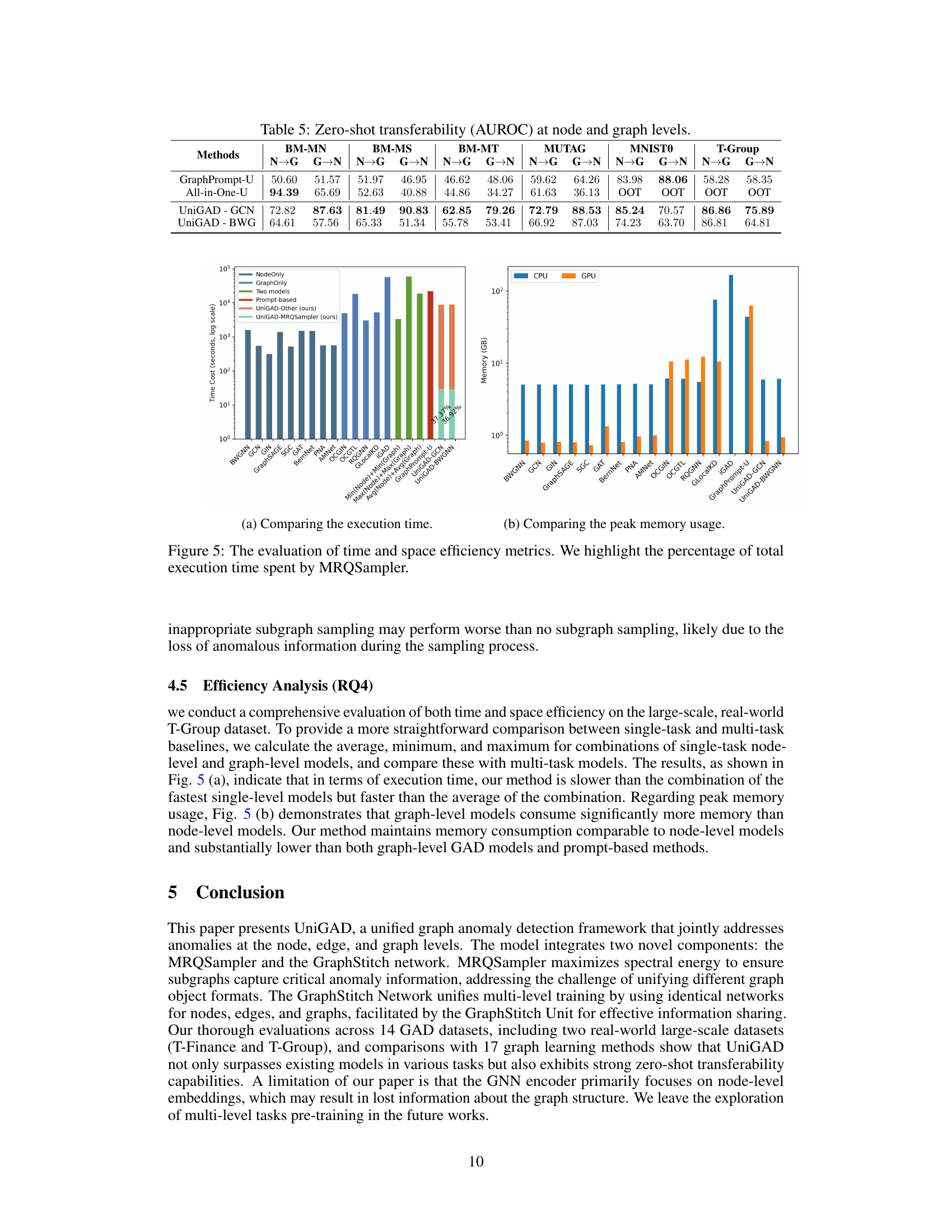
This table compares the performance of UniGAD against various single-level and multi-task methods on seven multi-graph datasets for node-level and graph-level anomaly detection. The AUROC (Area Under the Receiver Operating Characteristic curve) metric is used to evaluate performance. The table shows that UniGAD consistently outperforms other methods on most datasets for both tasks.
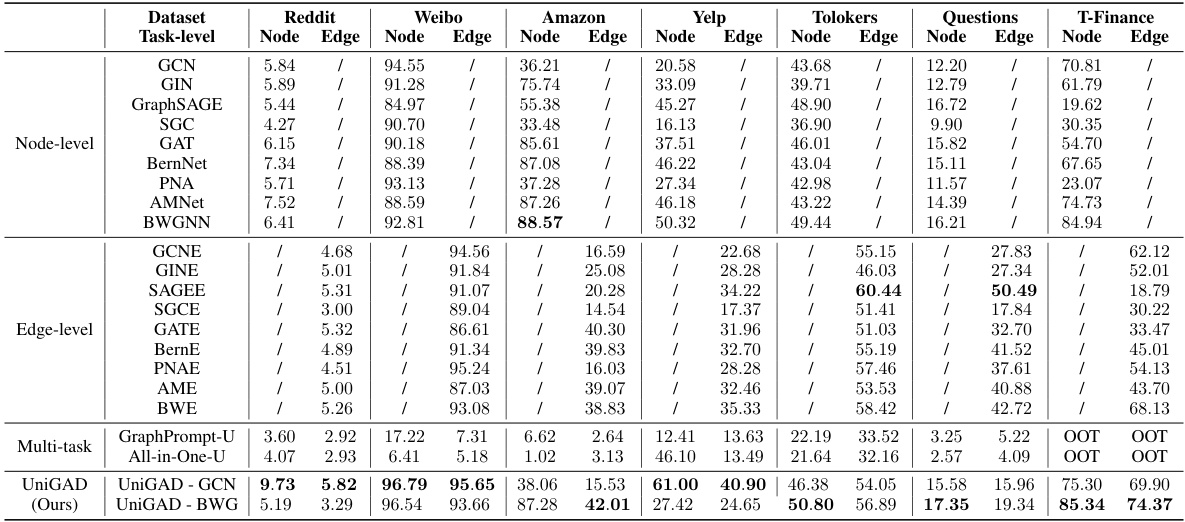
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) for node-level and edge-level anomaly detection across several datasets. It compares the performance of UniGAD against various single-task and multi-task methods, highlighting UniGAD’s superior performance in a unified multi-level approach.

This table compares the Area Under the Receiver Operating Characteristic Curve (AUROC) achieved by UniGAD against various single-level and multi-task methods for node-level and edge-level anomaly detection on six datasets. It showcases UniGAD’s performance relative to existing state-of-the-art models on various graph datasets, demonstrating the effectiveness of its unified approach in handling multi-level tasks.

This table compares the area under the receiver operating characteristic curve (AUROC) for node-level and edge-level anomaly detection across various methods. It includes results for single-level methods (GCN, GIN, etc.), multi-task methods (GraphPrompt-U, All-in-One-U), and the proposed UniGAD method (with GCN and BWGNN backbones). The table allows for a comparison of the performance of different methods across multiple datasets, showing how UniGAD’s unified approach performs in comparison to methods that handle node and edge anomalies separately.

This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) results for various graph anomaly detection methods across seven datasets. The methods are categorized into single-level (node-level and graph-level), multi-task, and the proposed UniGAD method. UniGAD is tested using two different backbone GNNs (GCN and BWGNN). The table allows for comparison of the performance of different methods across different tasks (node-level and graph-level anomaly detection).
Full paper#