↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world applications require algorithms that can efficiently process and update solutions in response to continuously changing data streams. Dynamic submodular maximization tackles this challenge, but existing algorithms often suffer from slow update times. This significantly limits their applicability for large-scale problems.
This research introduces a novel algorithm that improves update speed by incorporating predictions about future data changes. The algorithm utilizes a combination of pre-processing based on predictions and a fast dynamic update mechanism, which results in a dramatically faster amortized update time, effectively addressing the limitation of prior algorithms. This improvement is achieved without sacrificing the quality of the approximation results, making it a practical and efficient solution for dynamic submodular maximization problems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in submodular optimization and dynamic algorithms. It directly addresses the challenge of slow update times in dynamic settings, a major bottleneck in many large-scale applications. The innovative use of predictions to accelerate algorithms opens new avenues for research, particularly in handling streaming data efficiently. The results are broadly applicable to various problems dealing with dynamic data, making it a valuable resource for a wide range of researchers.
Visual Insights#
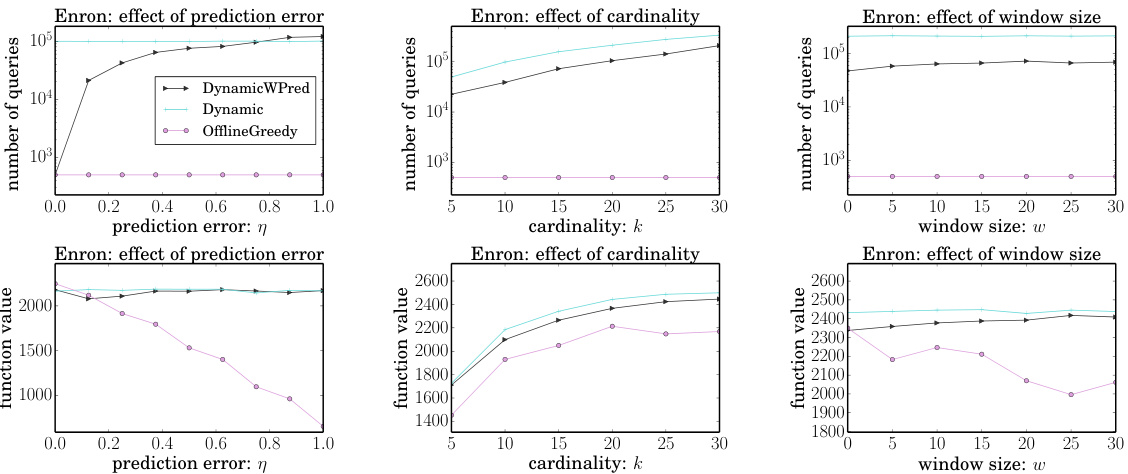
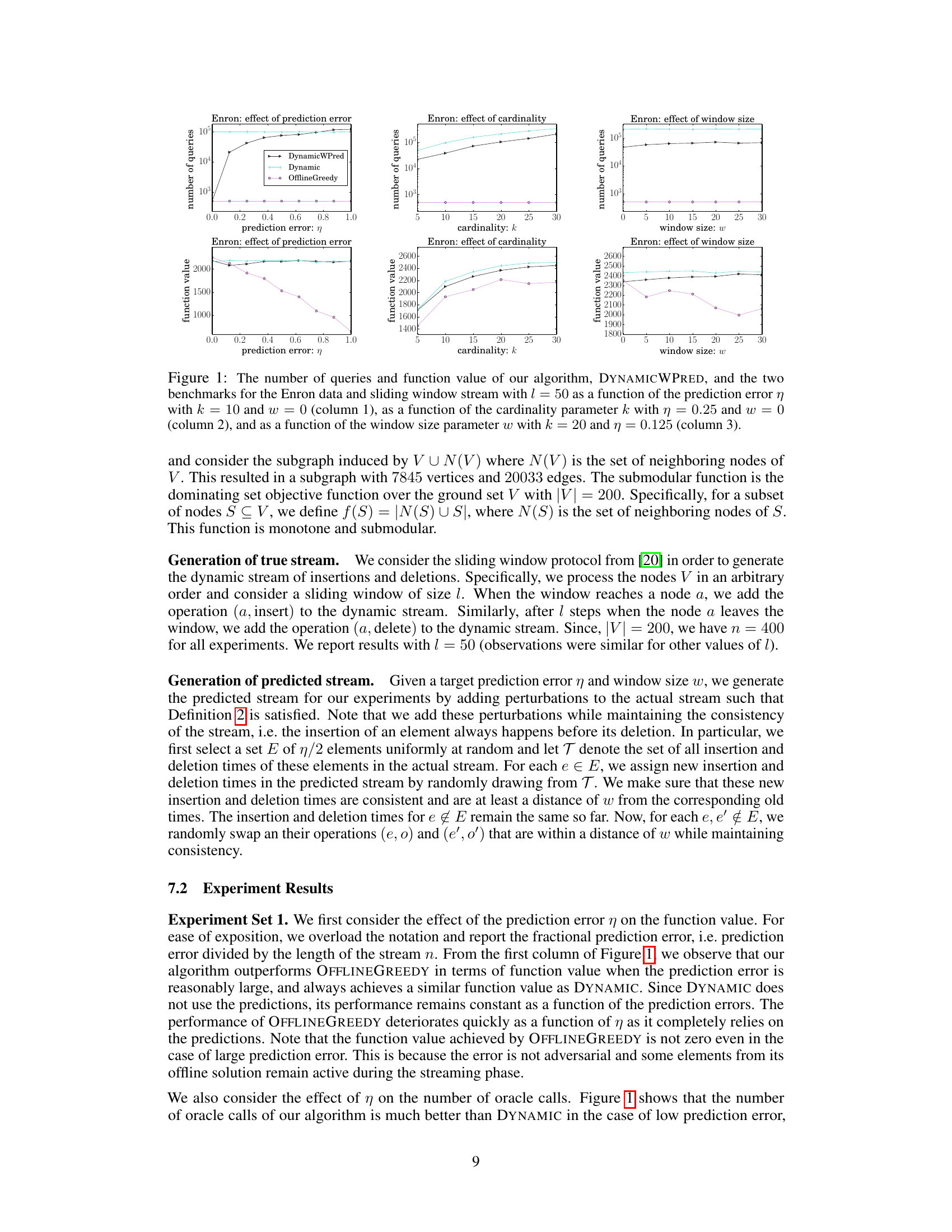
This figure shows the experimental results on the Enron dataset using a sliding window stream. It presents the number of queries and function values achieved by three algorithms: DYNAMICWPRED (the proposed algorithm), DYNAMIC (an algorithm without predictions), and OFFLINEGREEDY (an algorithm that uses predictions but is highly sensitive to prediction errors). The results are shown as functions of prediction error (η), cardinality (k), and window size (w). The figure helps evaluate the performance and robustness of DYNAMICWPRED under various conditions and in comparison to the other approaches.

This figure compares the performance of three algorithms: DYNAMICWPRED, DYNAMIC, and OFFLINEGREEDY. It shows the number of queries and the function value achieved by each algorithm under various conditions. Specifically, it explores how these metrics change as the prediction error (η), cardinality (k), and window size (w) vary, providing a comprehensive evaluation of the algorithms’ efficiency and effectiveness across different settings.
Full paper#