Detecting and Measuring Confounding Using Causal Mechanism Shifts

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in causal inference because it offers novel measures for detecting and quantifying confounding effects, even in the presence of unobserved confounders. This significantly advances causal discovery and enhances the reliability of causal effect estimation, impacting various fields relying on observational data.

Visual Insights

#

This figure illustrates three different settings for measuring confounding between two variables Xi and Xj, potentially influenced by an unobserved confounder Z. Each setting leverages different contextual information and methods to quantify confounding: Setting 1 uses directed information, Setting 2 employs causal mechanism shifts in Z, and Setting 3 incorporates knowledge of the causal path direction between Xi and Xj.

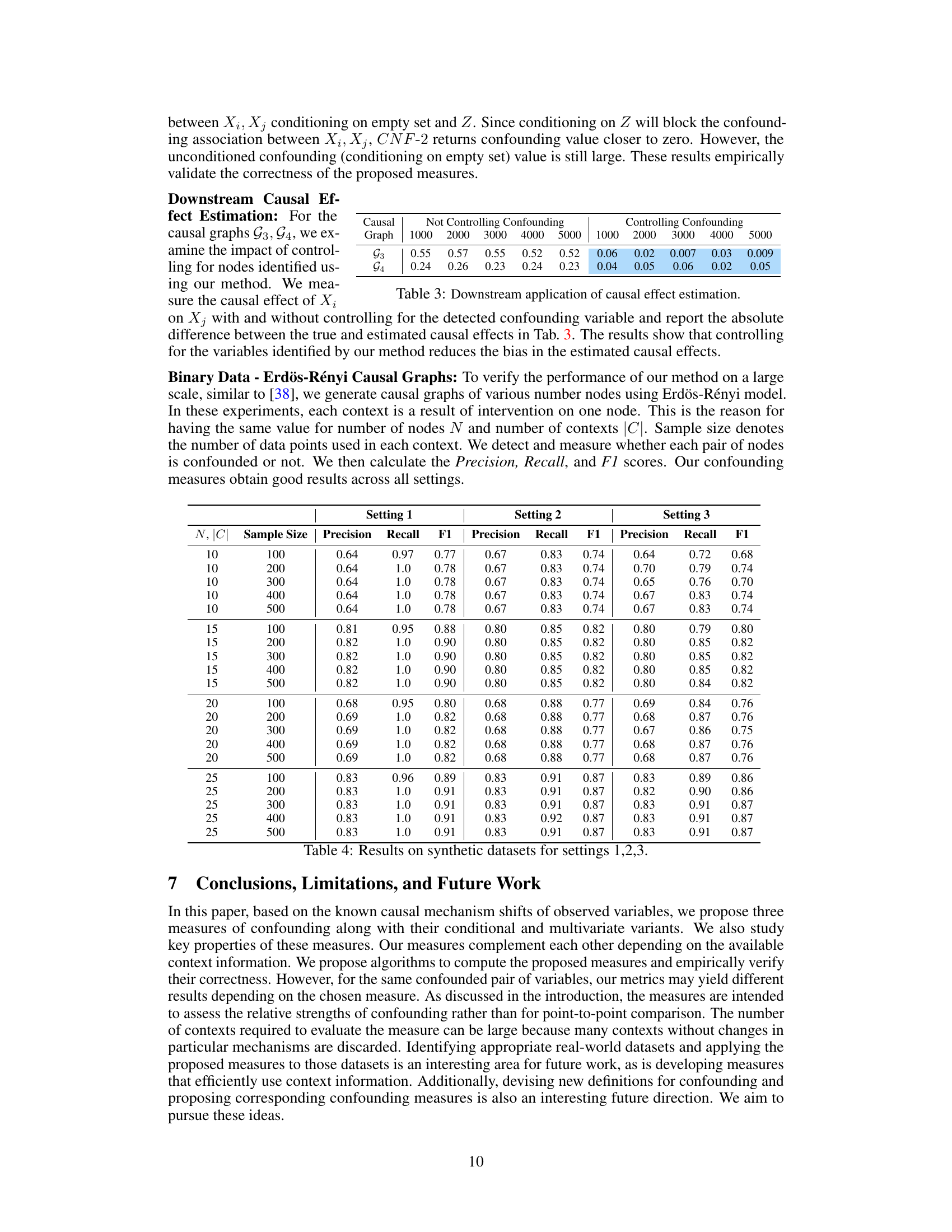
This table summarizes the different settings used to detect and measure confounding in the paper. It shows three settings, each based on different assumptions about available data and interventions. Setting 1 leverages directed information and non-collapsibility, requiring hard/structural interventions. Settings 2 and 3 rely on mutual information with soft/parametric interventions.

In-depth insights

#

Causal Mechanism Shifts

#

The concept of “Causal Mechanism Shifts” proposes that changes in the causal relationships between variables can be leveraged to understand and measure confounding. This approach moves away from traditional causal sufficiency assumptions, which often are unrealistic and empirically untestable. By observing data from multiple contexts where causal mechanisms have shifted, it becomes possible to identify and quantify confounding effects, separating observed from unobserved confounding. The methods proposed aim to assess the relative strengths of confounding between variable sets, providing a more comprehensive view than simply detecting the presence or absence of confounding. A key strength is its ability to handle unobserved confounding variables, a persistent challenge in causal inference. The framework introduces various measures of confounding, tailored to different scenarios and incorporating information from multiple contexts, supporting practical application and interpretation of results. These advances can potentially enhance the accuracy and reliability of causal inferences drawn from observational data.

Confounding Measures

#

The concept of “Confounding Measures” in causal inference is crucial for reliably estimating causal effects. A confounding variable distorts the relationship between variables of interest, leading to inaccurate conclusions. Therefore, robust methods for quantifying and addressing confounding are essential. This involves not just detecting confounding variables but also assessing their strength of influence. Different measures capture different aspects of confounding, reflecting various assumptions and characteristics of the data. Some methods might focus on the magnitude of bias introduced by confounders, while others might quantify the degree to which observed associations are attributable to the confounder versus other causal mechanisms. The selection of an appropriate measure depends on the specific research context and data properties. An ideal confounding measure should be interpretable, easily calculable, and robust to violations of assumptions. Moreover, it should offer insights into how to best adjust for or mitigate the effects of confounding, leading to more precise and reliable causal estimates. The development and comparison of different confounding measures remains an active area of research and it is crucial to consider the limitations and implications of each approach.

Multi-context Analysis

#

Multi-context analysis, in the context of causal inference, offers a powerful approach to address the challenges posed by confounding. Leveraging data from multiple contexts, where each context represents a different set of environmental conditions or interventions, allows researchers to disentangle spurious correlations from genuine causal effects. By carefully studying how causal relationships change across contexts, it becomes possible to identify confounding variables and more accurately estimate causal effects, which addresses limitations of traditional methods that often rely on unrealistic assumptions like causal sufficiency. The strength of this approach lies in its ability to reveal hidden confounders and to assess the relative strength of confounding bias, thereby leading to more robust and reliable causal inference. However, successful implementation depends on the careful selection and characterization of contexts, ensuring sufficient variation while controlling for extraneous factors. Methodological challenges may include determining appropriate statistical techniques to analyze data across diverse contexts and formulating assumptions that maintain rigor while allowing for flexibility in the modeling approach. Despite these challenges, multi-context analysis represents a promising avenue for more nuanced and robust causal understanding, particularly in situations where traditional causal discovery methods struggle.

Unobserved Confounding

#

Unobserved confounding presents a significant challenge in causal inference, as its presence violates the crucial assumption of causal sufficiency. It undermines the reliability of causal effect estimates derived from observational data, as spurious associations can arise due to the influence of hidden variables. Methods for addressing unobserved confounding often require strong assumptions, such as linearity or specific distributions, which may not hold in real-world scenarios. Identifying and mitigating the effects of unobserved confounding is critical for drawing valid causal conclusions, and various approaches, including those leveraging data from multiple environments or incorporating domain expertise, are continuously being developed to improve the accuracy and robustness of causal inference in the presence of unobserved confounding.

Future Research

#

Future research directions stemming from this work could explore several promising avenues. Extending the proposed confounding measures to more complex causal structures with numerous variables and intricate relationships is crucial. The current approach’s efficiency could also be improved. Developing more computationally efficient algorithms to address larger datasets and higher dimensionality would enhance applicability. Furthermore, investigating the robustness of the proposed methods under different data distributions and noise models is essential to broaden practical usage. Exploring hybrid approaches combining the strengths of various existing methods with the proposed measures could lead to improved accuracy. Finally, applying these advanced confounding analysis techniques to specific real-world applications across various domains (healthcare, climate science, social sciences) will be critical to validate their effectiveness and unlock new insights. A focus on developing easily interpretable visualizations of confounding effects is vital to make this analysis readily understandable and accessible to broader audiences.

More visual insights

#

More on figures

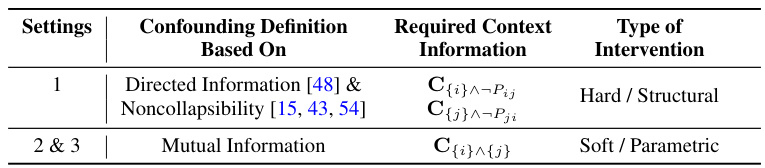
This figure displays the results of measuring confounding between two variables (Xi, Xj) using three different methods (CNF-1, CNF-2, CNF-3) across various sample sizes. The results are shown for four different causal graph structures (G1-G4). G1 and G2 represent unconfounded scenarios (empty graph and Xi→Xj, respectively), while G3 and G4 represent confounded scenarios (Z→Xi, Z→Xj and Z→Xi, Z→Xj, Xi→Xj respectively). The plots show that the confounding measures correctly output values near zero in the unconfounded cases and positive values in the confounded cases, demonstrating the methods’ effectiveness in detecting confounding.

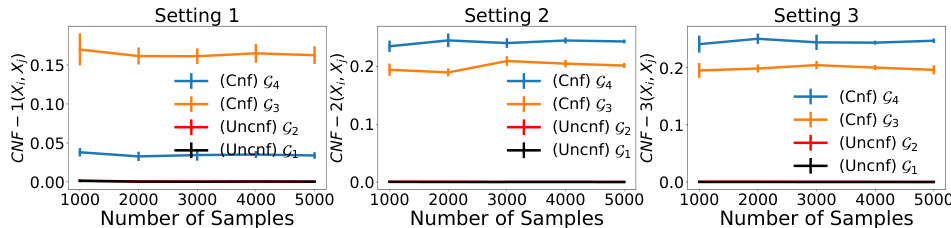
This figure shows the results of measuring conditional confounding using CNF-2 in two different causal structures (G5 and G6). G5 has two confounding variables, Z1 and Z2, while G6 has one (Z). The left panel illustrates that conditioning on either Z1, Z2, or neither, still results in positive conditional confounding values because the confounding relationship remains. Conversely, the right panel depicts that while conditioning on nothing results in positive confounding, conditioning on Z removes it, leading to a CNF-2 value closer to zero.

This figure shows two example graphs representing real-world scenarios where the proposed method can be applied to detect and measure confounding. The graphs illustrate two different sets of variables and their relationships, providing concrete examples of how the methods described in the paper can be used in practical applications.

More on tables

This table shows the values of directed information I(Xᵢ → Xⱼ) and I(Xⱼ → Xᵢ) for different causal graphs involving two or three nodes (Xᵢ, Xⱼ, Z). The table illustrates how the presence of confounding affects the values of directed information. When there’s no confounding between Xᵢ and Xⱼ, one of the directed information values will be zero; if there is confounding (via Z), both directed information values will be greater than zero.

This table presents the results of a downstream application of causal effect estimation. It shows the impact of controlling for confounding variables (identified using the proposed methods) on the accuracy of causal effect estimations. Two causal graphs (G3 and G4) with varying sample sizes (1000-5000) are used to compare causal effect estimations with and without controlling for confounding factors. The difference between the true and estimated causal effects is measured, demonstrating the effectiveness of confounding control in improving the accuracy of causal effect estimations.

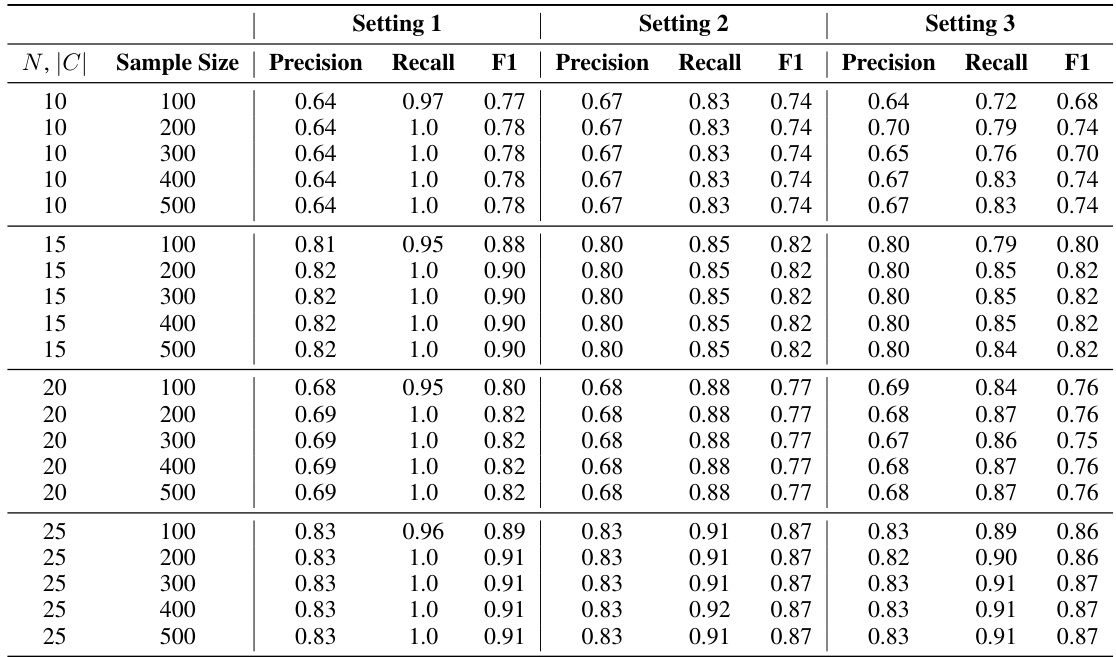
This table presents the results of experiments on synthetic datasets to evaluate the performance of three different confounding measures (CNF-1, CNF-2, CNF-3) under various conditions. The experiments use Erdos-Renyi generated causal graphs, varying the number of nodes (N), contexts (C), and sample sizes. The table reports precision, recall, and F1 scores for each measure across three settings, reflecting different assumptions about available contextual information and interventions. The results demonstrate the effectiveness of the measures in detecting confounding relationships.

Full paper

#