↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Hybrid deep generative models (DGMs), which integrate physics-based expressions into neural networks, are increasingly popular. However, a major challenge is their unidentifiability—multiple sets of parameters can generate the same data, hindering model interpretation and generalization. Existing studies have primarily focused on improving the learning of these models without addressing this identifiability issue. This paper presents a first theoretical investigation into the identifiability of hybrid DGMs and reveals that the existing methods using unconditional priors fail to guarantee identifiability.
The researchers propose a novel solution to this problem: meta-learning. By formulating the learning process as a meta-learning task, they establish the identifiability of hybrid DGMs. This is achieved by enforcing conditional independence among latent variables given few-shot context samples, a method inspired by nonlinear ICA. Their findings are supported by experiments on synthetic and real-world datasets, demonstrating superior identifiability and improved performance in predicting unseen data compared to other methods. This work contributes a new framework for building identifiable DGMs.
Key Takeaways#
Why does it matter?#
This paper is crucial because identifiability is fundamental for reliable model generalization and out-of-distribution robustness. It offers a novel meta-learning solution, impacting the design and interpretation of hybrid deep generative models across various fields. The theoretical framework opens new avenues for constructing identifiable generative models beyond hybrid-DGMs. This research directly addresses a significant limitation in the current deep learning landscape.
Visual Insights#
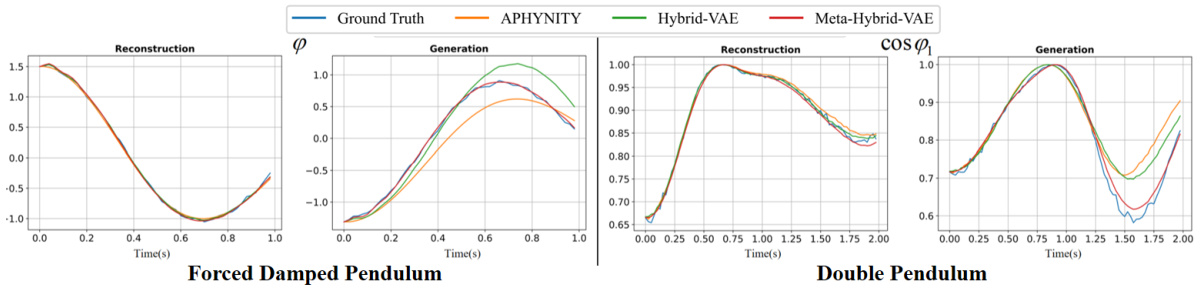
The figure displays visual results comparing the performance of three different models (APHYNITY, Hybrid-VAE, and Meta-Hybrid-VAE) on two synthetic datasets: Forced Damped Pendulum and Double Pendulum. For each dataset, the figure shows two subplots: reconstruction and generation. The reconstruction subplots show the model’s ability to reconstruct the observed data, while the generation subplots show the model’s ability to generate new data points. The ground truth data is also included for comparison. The purpose of the figure is to show visually that even when the reconstruction performance is similar across the models, the new Meta-Hybrid-VAE model significantly outperforms the other models in prediction tasks by generating trajectories closer to the ground truth.
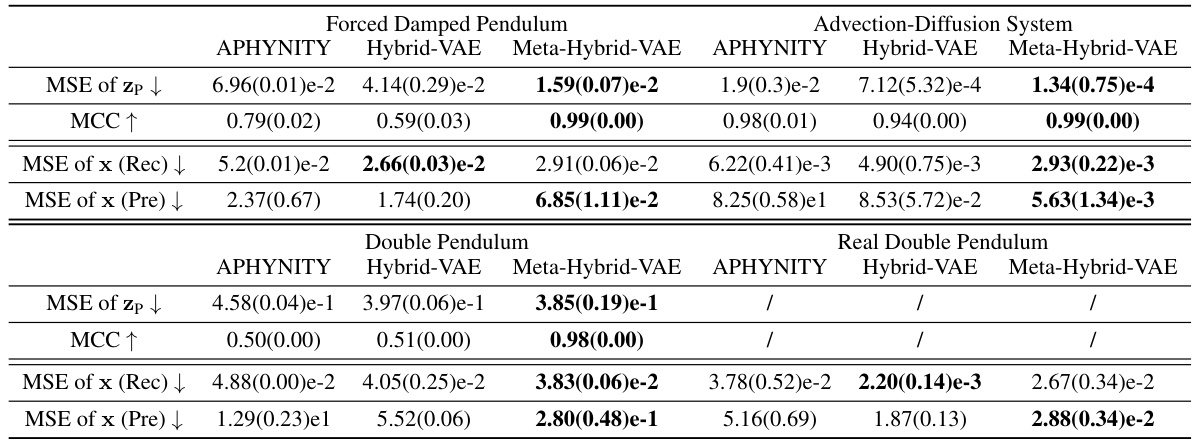
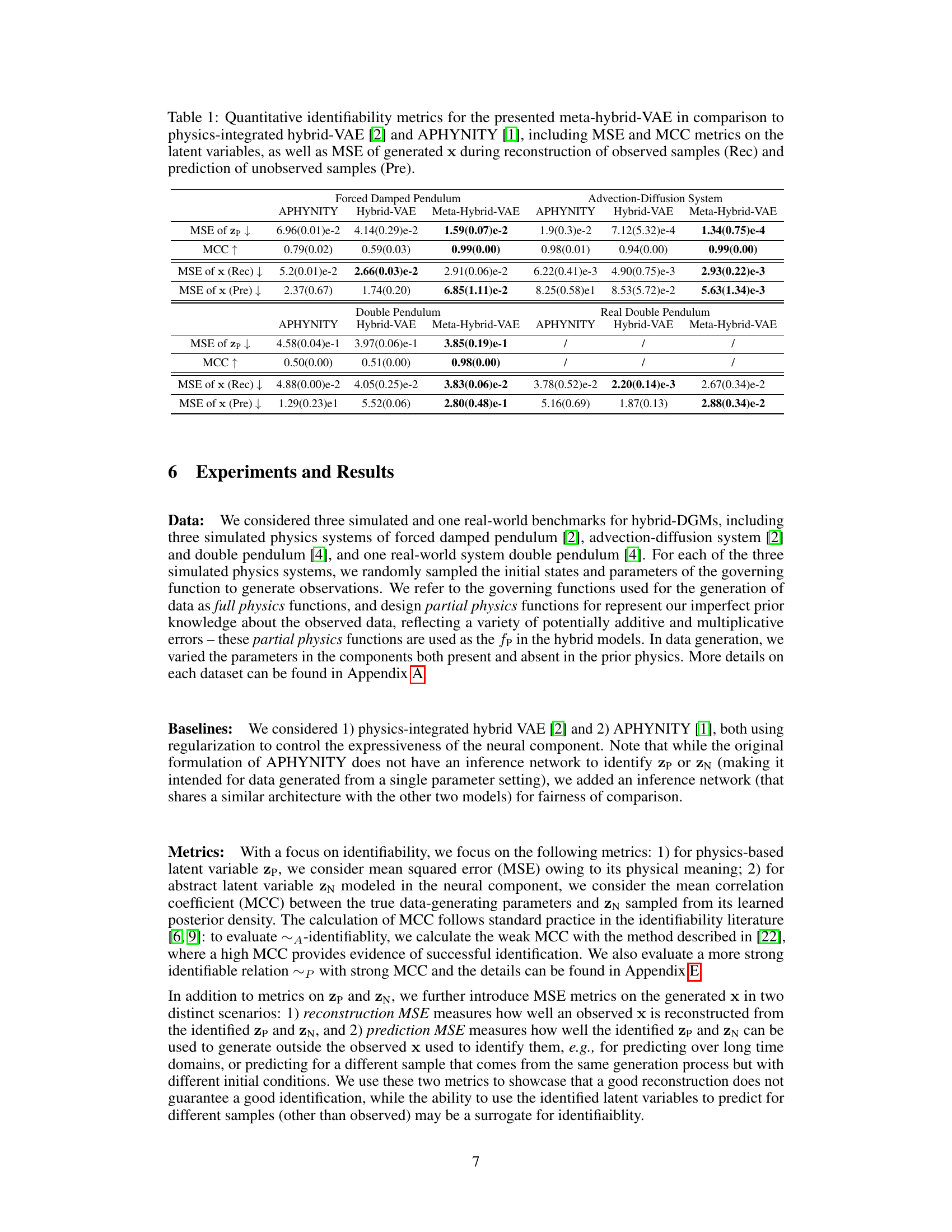
This table presents a quantitative comparison of the identifiability performance of three different hybrid VAEs: the proposed meta-hybrid VAE and two existing models (physics-integrated hybrid-VAE and APHYNITY). Identifiability is evaluated using Mean Squared Error (MSE) and Matthews Correlation Coefficient (MCC) for both the physics-based and neural latent variables. Additionally, MSE is calculated for the reconstruction and prediction of the observed samples, offering a comprehensive evaluation of each model’s ability to identify and generalize from the data.
In-depth insights#
Hybrid-DGM ID#
The heading ‘Hybrid-DGM ID’ likely refers to the identifiability problem within hybrid deep generative models (Hybrid-DGMs). Hybrid-DGMs combine physics-based and neural network components, presenting a challenge for parameter estimation. The ‘ID’ likely signifies the core issue: determining whether a given model’s parameters are uniquely recoverable from data. Unidentifiability arises when multiple parameter sets can generate the same data, rendering the model ambiguous. The paper likely investigates methods to ensure identifiability, perhaps through meta-learning approaches that leverage contextual information or impose constraints to resolve the ambiguity inherent in the combined physics and neural components. This is crucial because unidentifiable models are unreliable for prediction and lack the interpretability that motivates their development. Therefore, strategies for achieving identifiability are a key contribution, potentially focusing on conditions under which unique parameter solutions are guaranteed.
Meta-Learning Fix#
A ‘Meta-Learning Fix’ in the context of hybrid deep generative models (DGMs) would likely address the core issue of identifiability. Standard DGMs often suffer from unidentifiability, meaning multiple parameter sets can produce the same output distribution. Hybrid DGMs, combining physics-based and neural components, exacerbate this issue. A meta-learning approach might learn to identify the correct parameters not by directly optimizing the likelihood but by learning a model that predicts the correct parameters given a few-shot context dataset. This would involve training the meta-learner on many similar tasks, allowing it to generalize to unseen scenarios and thus resolve the identifiability problem. The resulting DGM would boast increased robustness and interpretability, as the identified parameters would reflect true underlying physics, rather than artifacts of the model’s training. The meta-learning fix would offer a strong theoretical foundation and demonstrate strong empirical results, potentially setting a new standard for identifiable hybrid DGMs.
Identifiability Theory#
The Identifiability Theory section likely delves into the core theoretical underpinnings of the research, addressing the fundamental question of whether the model parameters can be uniquely determined from the observed data. This is crucial because unidentifiable models can lead to ambiguous interpretations and unreliable predictions. The authors probably explore existing identifiability results for general deep generative models (DGMs) and discuss how these results apply, or don’t apply, to their specific hybrid DGM architecture. A key contribution would be the presentation of novel theoretical conditions or constraints under which their proposed hybrid model becomes identifiable, possibly leveraging concepts like conditional independence, specific structural assumptions about the model components, or meta-learning. They may provide rigorous mathematical proofs to support their claims of identifiability. The analysis would also discuss practical implications for model training and interpretation, highlighting how establishing identifiability enhances the model’s robustness, generalizability, and the reliability of inferences drawn from it.
Synthetic Data#
The use of synthetic data in evaluating hybrid deep generative models offers several crucial advantages. Synthetic datasets allow for precise control over the data-generating process, enabling researchers to isolate and study the impact of specific factors on model performance, such as noise levels, or the distribution of latent variables. This precise control facilitates a deeper understanding of the model’s behavior. Furthermore, synthetic data provides a reliable and consistent benchmark, which is particularly valuable when assessing the identifiability of hybrid models as it mitigates the influence of dataset biases and complexities present in real-world data. This helps isolate the true performance of the model. However, a limitation of synthetic data is its potential for limited generalizability to real-world scenarios. While synthetic data enables focused investigations, it is crucial to validate findings using real-world data. To fully understand a hybrid model’s capabilities and limitations, both synthetic and real datasets must be employed. A careful consideration of both the strengths and weaknesses of synthetic data is essential for rigorous model evaluation.
Real-World Test#
A robust ‘Real-World Test’ section in a research paper would go beyond simply applying the model to a new dataset. It should include a detailed description of the real-world data, highlighting its complexity and any differences from the training data. The section needs to demonstrate the model’s generalizability and practical utility in a setting that isn’t perfectly controlled. Qualitative and quantitative results showcasing the model’s performance on key metrics specific to the application are essential, along with a thoughtful analysis comparing its strengths and limitations against existing methods or baselines applied in similar real-world scenarios. A discussion of unexpected behaviors, failures, or edge cases encountered during testing, and how these insights inform future improvements, would significantly enhance the validity and impact of the ‘Real-World Test’ section. Finally, addressing potential ethical considerations or societal implications arising from the real-world application would demonstrate responsible research practices.
More visual insights#
More on figures
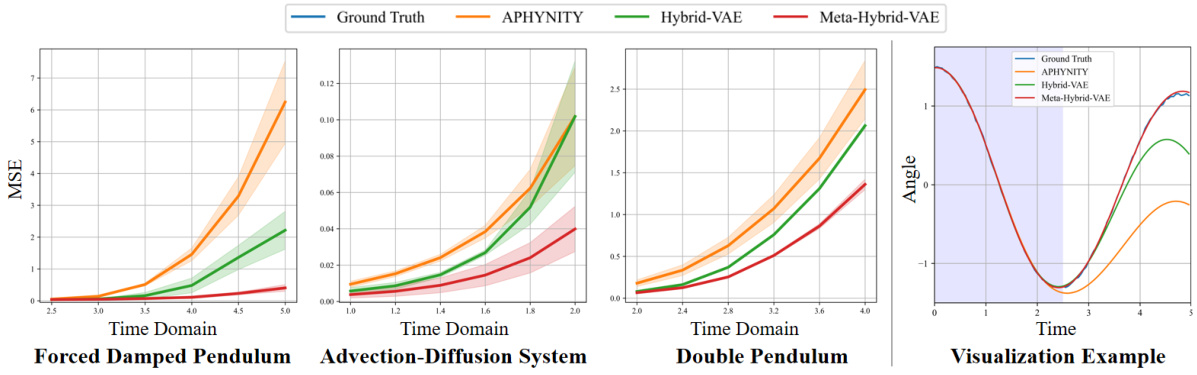
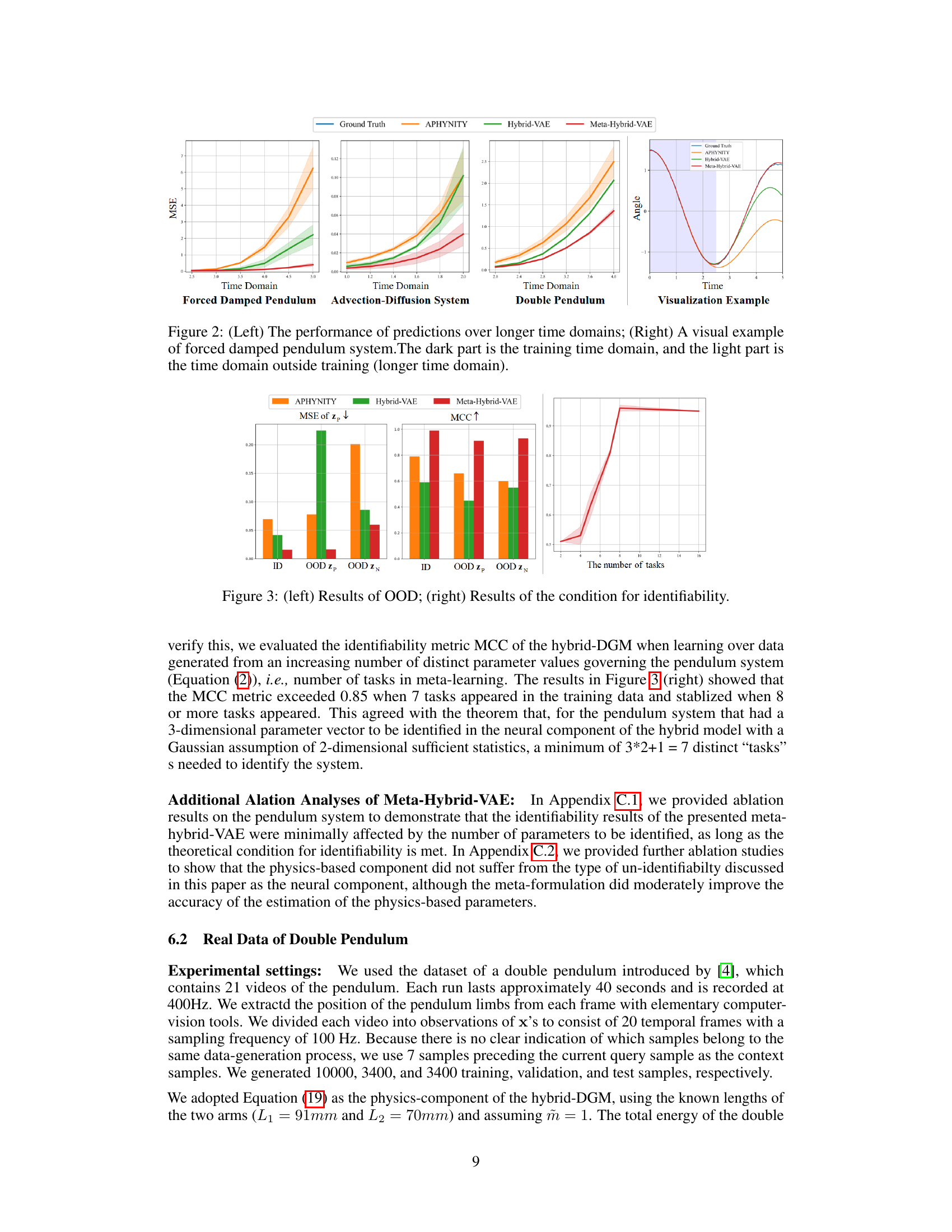
This figure visualizes the prediction performance of three different models (APHYNITY, Hybrid-VAE, and Meta-Hybrid-VAE) on three different datasets (Forced Damped Pendulum, Advection-Diffusion System, and Double Pendulum) over extended time periods. The left panel shows the MSE (Mean Squared Error) for each model across the three datasets, demonstrating the performance degradation as the prediction horizon extends beyond the training data. The right panel shows a visual representation of these prediction results on the Forced Damped Pendulum dataset, highlighting the performance differences of the models.

This figure presents results regarding out-of-distribution (OOD) performance and the verification of the condition for identifiability. The left panel shows a bar chart comparing the performance of three models (APHYNITY, Hybrid-VAE, and Meta-Hybrid-VAE) in both in-distribution (ID) and OOD settings, focusing on MSE of the physics latent variables (zp) and MCC of the abstract latent variables (zn). The right panel displays a line chart illustrating the relationship between the MCC metric and the number of tasks in the meta-learning process. This empirically verifies the theoretical condition for identifiability, showing a clear increase in MCC as the number of tasks reaches a threshold.

This figure compares the reconstruction and prediction performance of three different models (APHYNITY, Hybrid-VAE, and Meta-Hybrid-VAE) on synthetic datasets. The top row shows the ground truth data, while the subsequent rows display the results from each model. The left-hand side shows reconstruction performance, where the models attempt to reconstruct observed data points. The right-hand side shows prediction performance, where the models attempt to predict data points outside the training domain. The models are evaluated across three different datasets: Forced Damped Pendulum, Double Pendulum, and Advection-Diffusion System. The figure visually demonstrates that the Meta-Hybrid-VAE model shows superior prediction performance compared to the other models, especially for more complex systems like the Double Pendulum.

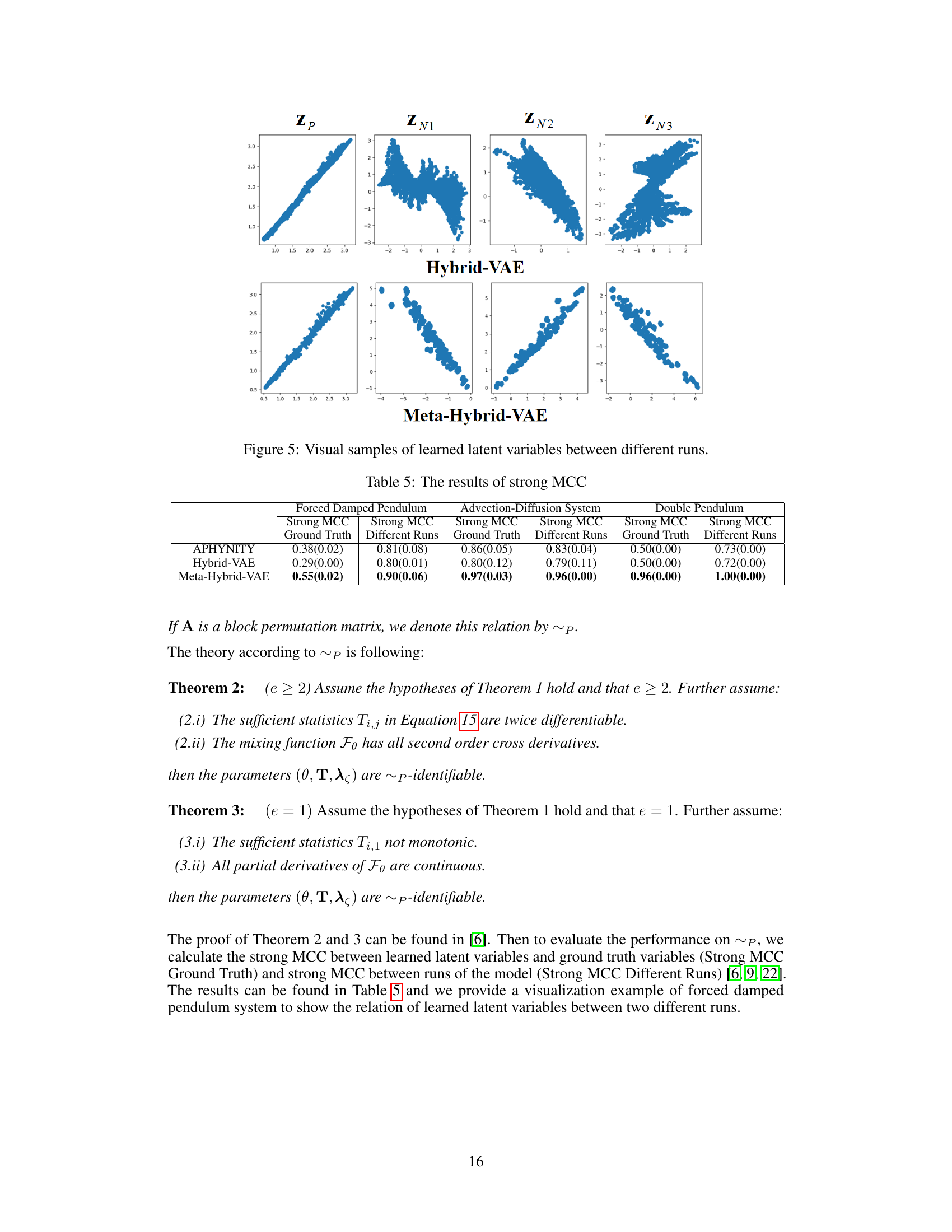
This figure visualizes the learned latent variables from two different runs of the Hybrid-VAE and Meta-Hybrid-VAE models. The top row shows the results for the Hybrid-VAE, while the bottom row shows the results for the Meta-Hybrid-VAE. Each column represents a different latent variable (Zp, ZN1, ZN2, ZN3). The plots show the relationship between the learned latent variables across the two different runs. The goal is to show the differences in the identifiability of the latent variables between the two models, with the Meta-Hybrid-VAE showing a clearer and more consistent relationship across different runs, indicating better identifiability.
More on tables

This table presents a comparison of quantitative identifiability metrics between the proposed meta-hybrid Variational Autoencoder (VAE) and two baseline methods: physics-integrated hybrid-VAE and APHYNITY. The metrics used include Mean Squared Error (MSE) and Matthews Correlation Coefficient (MCC) for latent variables (zp and zn), and MSE for the generated data x, broken down into reconstruction and prediction performance. Lower MSE values and higher MCC values indicate better identifiability.

This table compares the performance of Non-meta and Meta methods in terms of MSE of zp, MCC, MSE of x (Rec), and MSE of x (Pre). The results show that the Meta method achieves lower MSE of zp and MSE of x (Pre) while maintaining similar MCC and MSE of x (Rec).

This table presents a comparison of quantitative identifiability metrics for three different hybrid VAEs: the presented meta-hybrid VAE, the physics-integrated hybrid VAE from prior work, and APHYNITY. It evaluates performance using Mean Squared Error (MSE) and Matthews Correlation Coefficient (MCC) for latent variables (zp and zn), and also MSE for reconstruction and prediction of observed samples (x). Lower MSE values and higher MCC values indicate better identifiability.

This table presents a quantitative comparison of the identifiability of three different hybrid VAEs: the proposed meta-hybrid VAE, a physics-integrated hybrid VAE, and APHYNITY. Identifiability is measured using Mean Squared Error (MSE) and Matthews Correlation Coefficient (MCC) for both the physics-based and neural latent variables. Additionally, it shows the MSE of the generated data (x) for both reconstruction and prediction tasks, allowing a comparative evaluation of the models’ ability to accurately learn and generalize from data.
Full paper#