↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Multi-agent reinforcement learning (MARL) excels in strategic game playing and real-world applications such as autonomous driving, but often faces privacy challenges when dealing with sensitive user data. Existing differential privacy mechanisms struggle to provide strong privacy protection in the dynamic MARL setting. This limits the application of MARL to scenarios involving sensitive user information.
This research introduces a new algorithm called DP-Nash-VI that addresses this challenge. DP-Nash-VI combines optimistic Nash value iteration with a novel privacy mechanism to guarantee trajectory-wise privacy while maintaining near-optimal regret bounds. This work extends the definition of differential privacy to two-player zero-sum episodic Markov games and provides the first results on trajectory-wise privacy protection in MARL.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between multi-agent reinforcement learning and differential privacy, a critical area for real-world applications involving sensitive data. The proposed algorithm and theoretical framework provide a strong foundation for future research, potentially leading to safer and more privacy-preserving AI systems in various domains like autonomous driving and online gaming. Its rigorous analysis and near-optimal regret bounds make it a valuable contribution to the field.
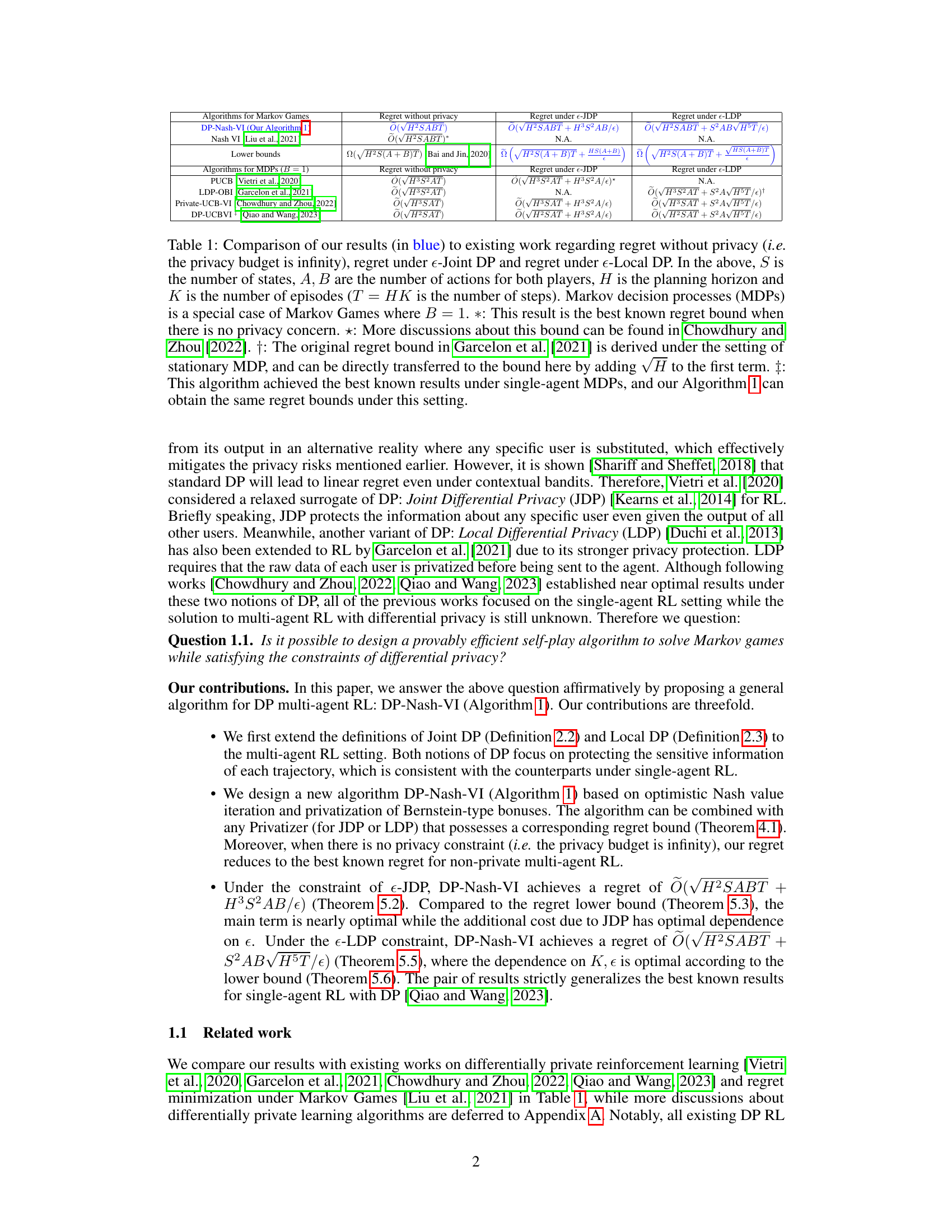
Visual Insights#

This table compares the regret bounds (a measure of performance) of different algorithms for solving Markov Games (a type of game used in reinforcement learning) under various conditions. It contrasts the regret without any privacy constraints, with the regret under e-Joint Differential Privacy (e-JDP) and e-Local Differential Privacy (e-LDP). The table shows that the proposed algorithm (DP-Nash-VI) achieves comparable or better regret bounds than existing methods, even when considering privacy constraints. The different algorithms are categorized as algorithms designed for Markov Games and algorithms specifically optimized for Markov Decision Processes (MDPs, a simpler case of Markov Games). The table clearly shows the superior performance of the new algorithm, especially in the context of privacy.
Full paper#