C-GAIL: Stabilizing Generative Adversarial Imitation Learning with Control Theory

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it tackles the instability problem in Generative Adversarial Imitation Learning (GAIL), a significant hurdle in reinforcement learning. By applying control theory, it provides a novel theoretical framework for understanding and improving GAIL’s training stability. This offers a more stable and efficient method for imitation learning, potentially impacting various applications. The findings also open up new research avenues in combining control theory with deep learning for improved convergence and stability in other adversarial learning algorithms.

Visual Insights

#

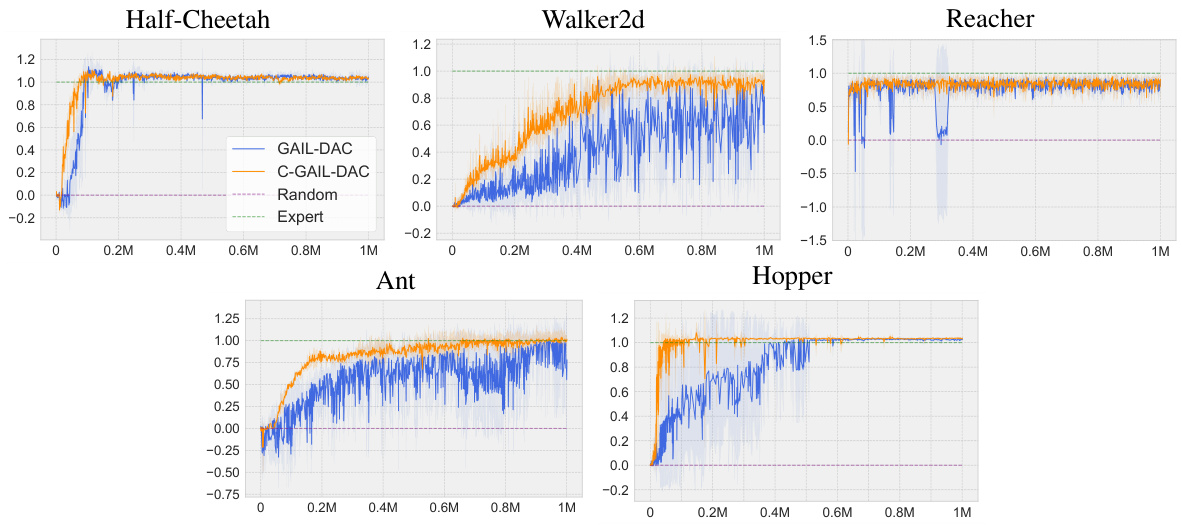
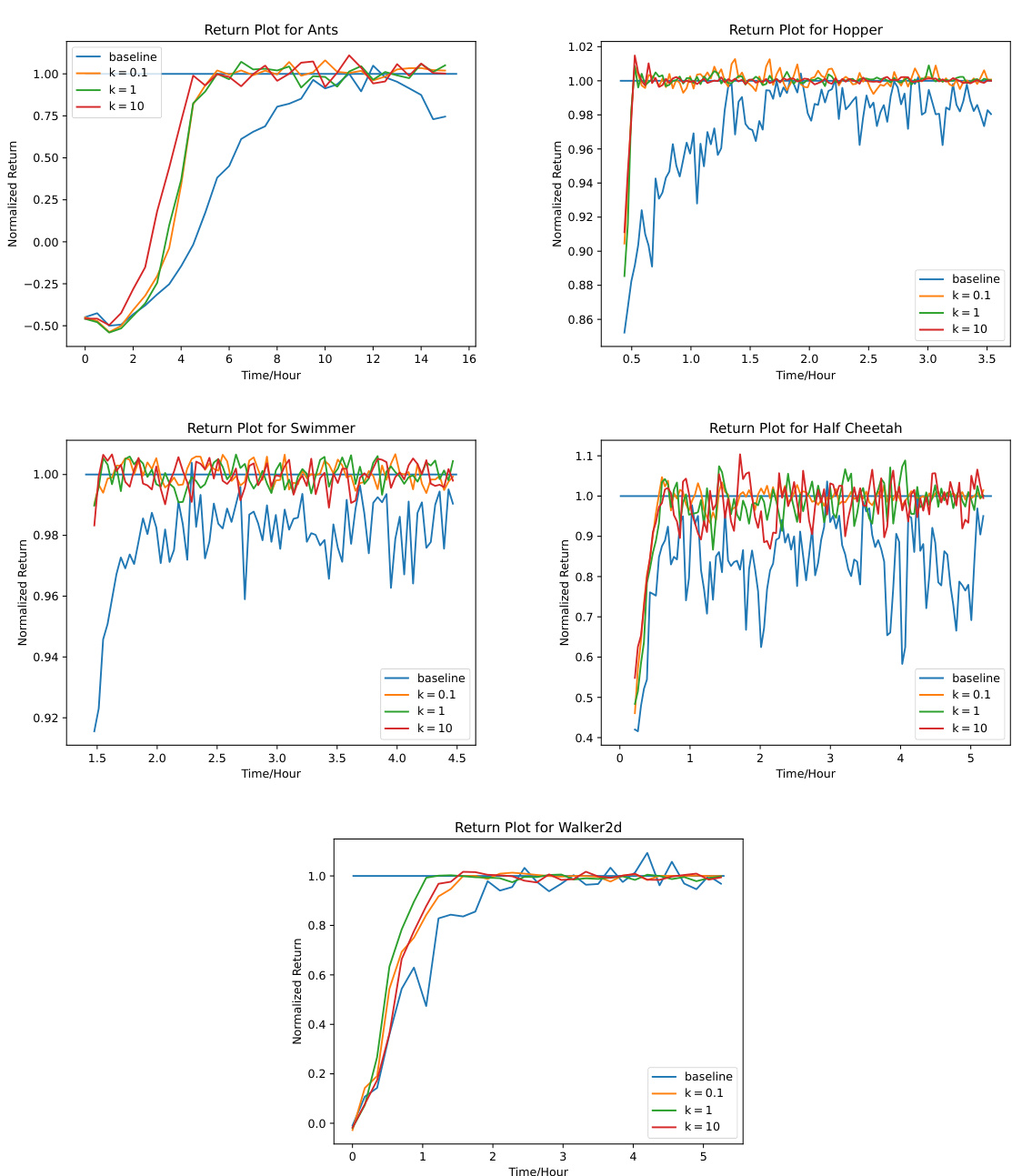
This figure displays the normalized return curves for the GAIL-DAC algorithm with a control mechanism (C-GAIL-DAC) compared against the standard GAIL-DAC and a random policy. The experiment uses four expert demonstrations across five different MuJoCo environments. The x-axis shows the number of gradient steps (in millions), and the y-axis indicates the normalized return, with 1 representing the expert policy’s performance and 0 representing a random policy. The results are averaged over five different random seeds to show the stability and convergence speed of the methods. C-GAIL-DAC demonstrates faster convergence and reduced oscillation compared to the standard GAIL-DAC, indicating improved training stability.

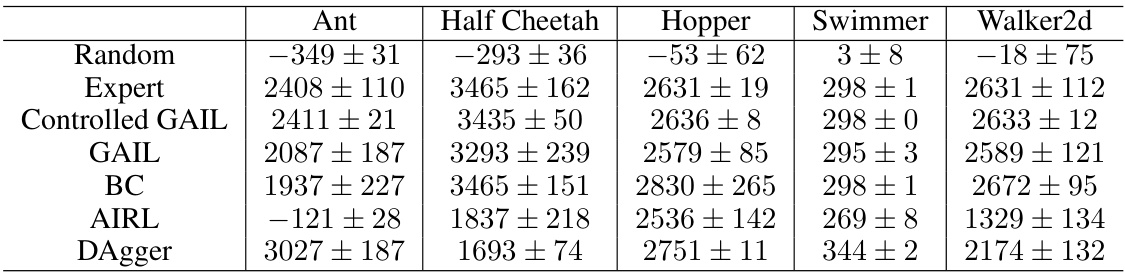
This table presents a comparison of the mean and standard deviation of returns achieved by different imitation learning (IL) algorithms across five MuJoCo environments. The algorithms compared include: Random (a baseline representing random actions), Expert (the performance of the expert policy being imitated), Controlled GAIL, GAIL, Behavior Cloning (BC), Advantage Weighted Regression (AIRL), and Dataset Aggregation (DAgger). The table provides a quantitative assessment of the relative performance of these algorithms in learning to mimic expert behavior across different control tasks.

In-depth insights

#

GAIL Instability

#

Generative Adversarial Imitation Learning (GAIL) suffers from training instability, a significant hurdle hindering its widespread adoption. The core issue stems from the inherent minimax nature of GAIL, where the generator and discriminator are locked in an adversarial game. This dynamic often leads to oscillations in the training loss, preventing convergence to a desirable equilibrium where the generated policy effectively mimics the expert. The instability is further exacerbated by the difficulty of balancing exploration and exploitation, as well as the sensitivity to hyperparameter choices. Control theory offers a promising framework for analyzing and addressing GAIL’s instability, providing tools to design controllers that regulate the training dynamics and ensure convergence to a stable solution. This approach provides both theoretical guarantees and practical improvements to existing GAIL algorithms, achieving faster convergence rates, reduced oscillations, and improved policy performance. Addressing GAIL’s instability is crucial to realizing the full potential of imitation learning, enabling the efficient training of high-performing policies in complex environments.

Control-Theoretic Analysis

#

A control-theoretic analysis of Generative Adversarial Imitation Learning (GAIL) offers a powerful lens to understand its training dynamics and instability. By modeling GAIL as a dynamical system, researchers can leverage control theory to analyze its convergence properties. A key insight is that GAIL, in its standard form, might not converge to the desired equilibrium, where the generated policy perfectly matches the expert. This is because the standard formulation might lack the necessary conditions for asymptotic stability. Therefore, a control-theoretic perspective is crucial for identifying the root causes of instability and designing novel controllers to stabilize the training process. These controllers can then be incorporated into the GAIL objective as differentiable regularizers, leading to improved convergence speed, reduced oscillations, and better policy performance. This approach demonstrates the effectiveness of combining machine learning and control theory, providing a robust and theoretically grounded framework for improving the performance of imitation learning algorithms.

C-GAIL Regularizer

#

The C-GAIL regularizer is a novel contribution designed to address the instability inherent in Generative Adversarial Imitation Learning (GAIL). GAIL’s training often suffers from oscillations and slow convergence, hindering its ability to effectively learn from expert demonstrations. By analyzing GAIL through the lens of control theory, the authors identify the cause of this instability and propose a differentiable regularization term that stabilizes the training dynamics. This regularizer acts as a controller, gently guiding the learning process towards a desired equilibrium where the generated policy closely matches the expert. Empirically, the C-GAIL regularizer consistently improves the performance of existing GAIL algorithms, speeding up convergence, reducing oscillations, and enhancing the learned policy’s ability to match the expert distribution. The theoretical underpinnings and the empirical results demonstrate the effectiveness of this technique, providing a valuable tool for practitioners seeking to apply GAIL to real-world problems. The regularizer’s pragmatic nature makes it easily adaptable to various GAIL methods, increasing its utility and applicability within the broader imitation learning landscape.

Empirical Validation

#

An empirical validation section in a research paper would rigorously test the proposed method’s effectiveness. It should compare the novel approach against existing state-of-the-art methods using multiple relevant datasets. The results should be presented clearly, likely with tables and figures showing key performance metrics, such as accuracy, precision, recall, F1-score, or other relevant metrics depending on the research area. Statistical significance testing would be crucial to demonstrate that observed improvements are not due to random chance. The section should also discuss any limitations observed during the empirical validation, potential sources of error, and the robustness of the proposed method under various conditions. A thorough analysis of both the strengths and weaknesses, along with potential reasons for unexpected outcomes, is vital. The discussion should explicitly address the research question and whether the empirical findings support or refute the hypotheses, clearly linking back to the theoretical underpinnings.

Future Works

#

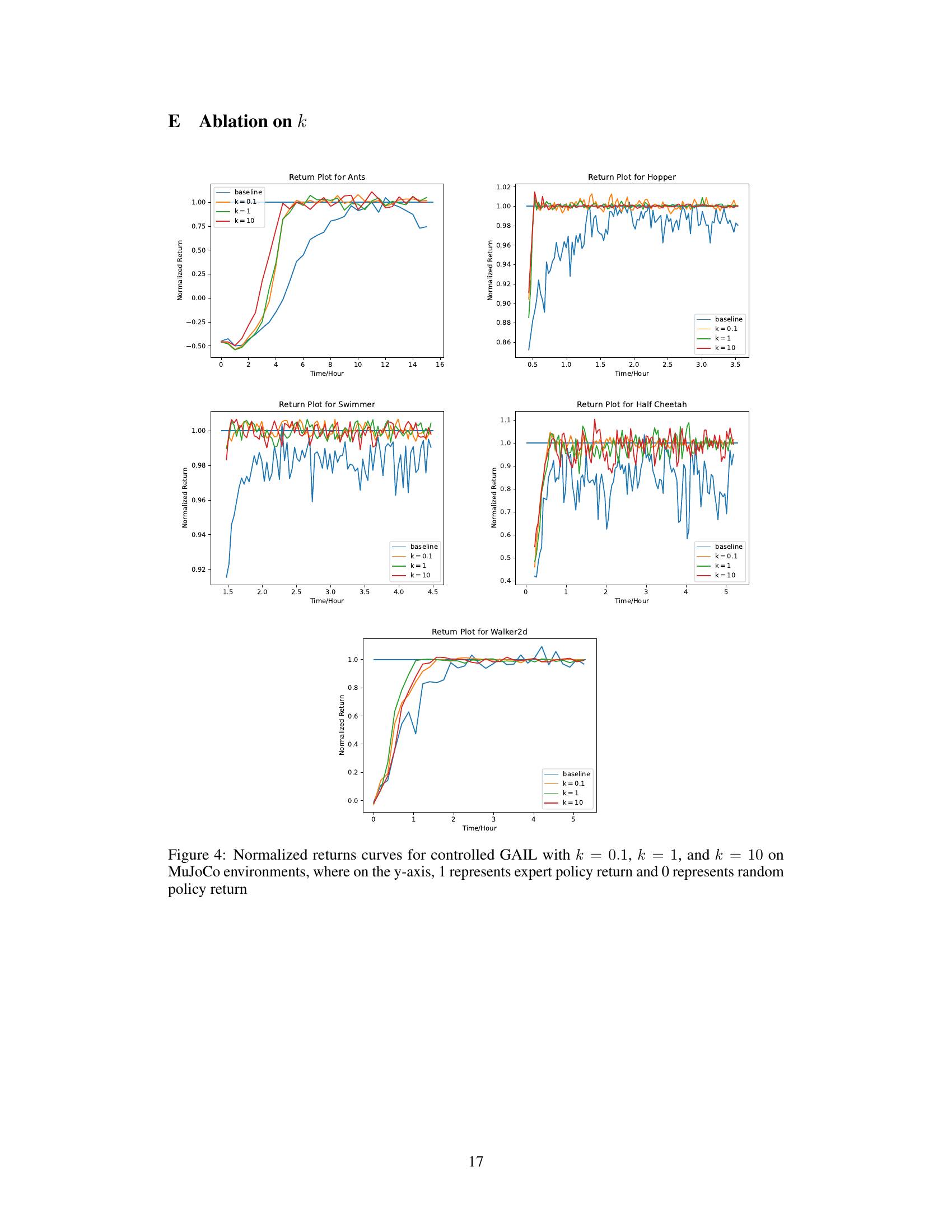
Future work could explore several promising directions. Extending the theoretical analysis beyond the one-step simplification would enhance the understanding of C-GAIL’s stability in more realistic scenarios. Investigating the impact of different controller designs and hyperparameter tuning methods could further optimize performance and robustness. Applying C-GAIL to a wider range of imitation learning tasks, including those with high-dimensional state and action spaces or sparse reward signals, would demonstrate its generalizability. Finally, combining C-GAIL with other advanced techniques, such as model-based reinforcement learning or curriculum learning, is also worth investigating to further improve sample efficiency and learning speed. A thorough empirical comparison with state-of-the-art methods across diverse benchmarks would solidify its position and identify potential limitations.

More visual insights

#

More on figures

This figure compares the performance of GAIL-DAC and C-GAIL-DAC in terms of how well the learned policy matches the expert policy’s state distribution. The x-axis represents the number of gradient steps (updates) during training. The y-axis represents the Wasserstein distance between the state distributions of the expert and the learned policy. A lower Wasserstein distance indicates a closer match between the two distributions. The figure shows that C-GAIL-DAC consistently achieves a lower Wasserstein distance than GAIL-DAC across all five MuJoCo environments, demonstrating that the controlled variant more closely matches the expert distribution.

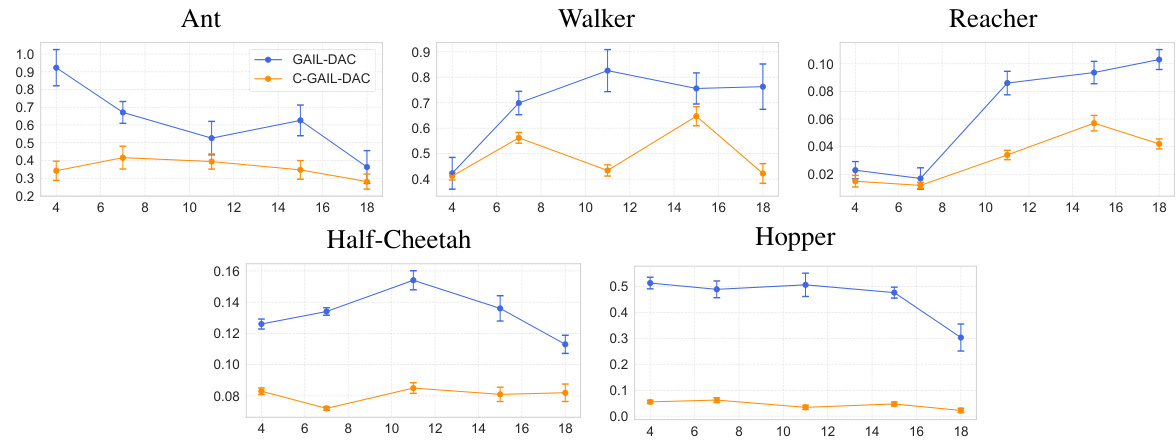
This figure compares the performance of GAIL-DAC and C-GAIL-DAC in terms of how well the learned policy matches the expert policy’s state distribution. The y-axis represents the Wasserstein distance, a measure of the difference between two probability distributions. A lower Wasserstein distance indicates a better match between the learned and expert policies. The x-axis represents the number of gradient steps during training. The plots show that C-GAIL-DAC consistently achieves a lower Wasserstein distance than GAIL-DAC across all five MuJoCo environments, indicating that the learned policy in C-GAIL-DAC more closely resembles the expert policy’s state distribution.

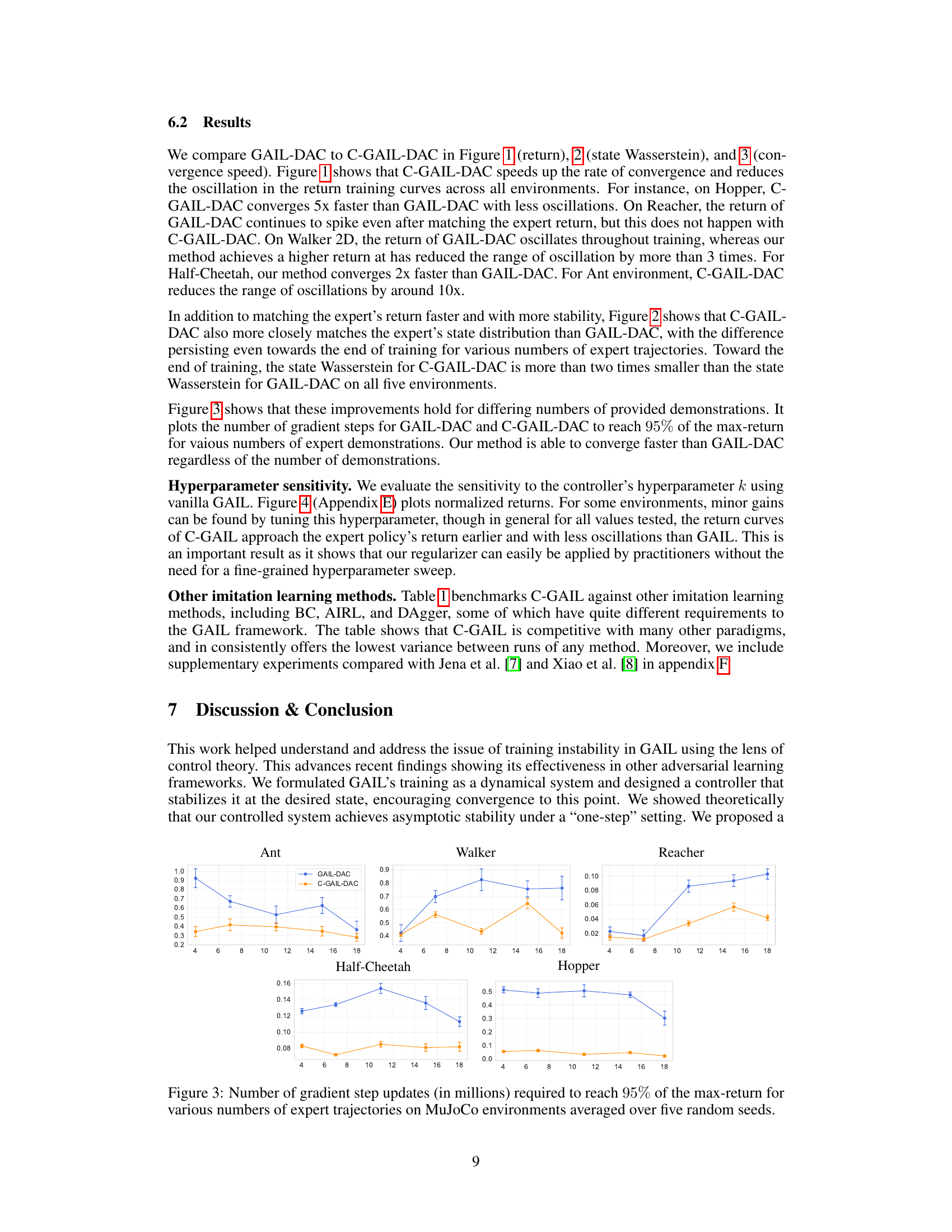
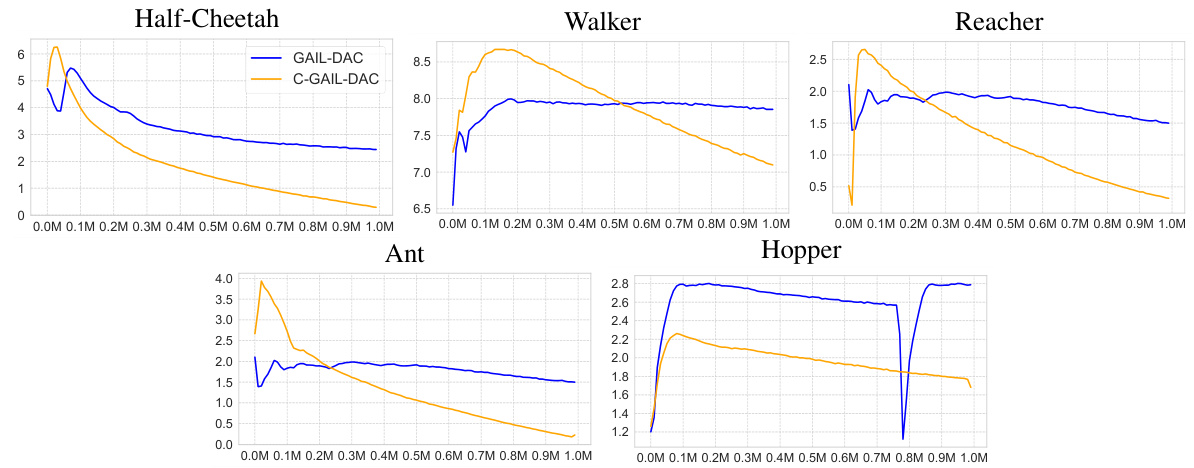
The figure shows the training curves of the GAIL-DAC algorithm with and without the proposed controller (C-GAIL-DAC) across five different MuJoCo environments. The x-axis represents the number of gradient updates, and the y-axis represents the normalized return (reward), scaled from 0 (random policy) to 1 (expert policy). The plot demonstrates that C-GAIL-DAC converges faster and with less oscillation than GAIL-DAC, indicating improved training stability.

More on tables

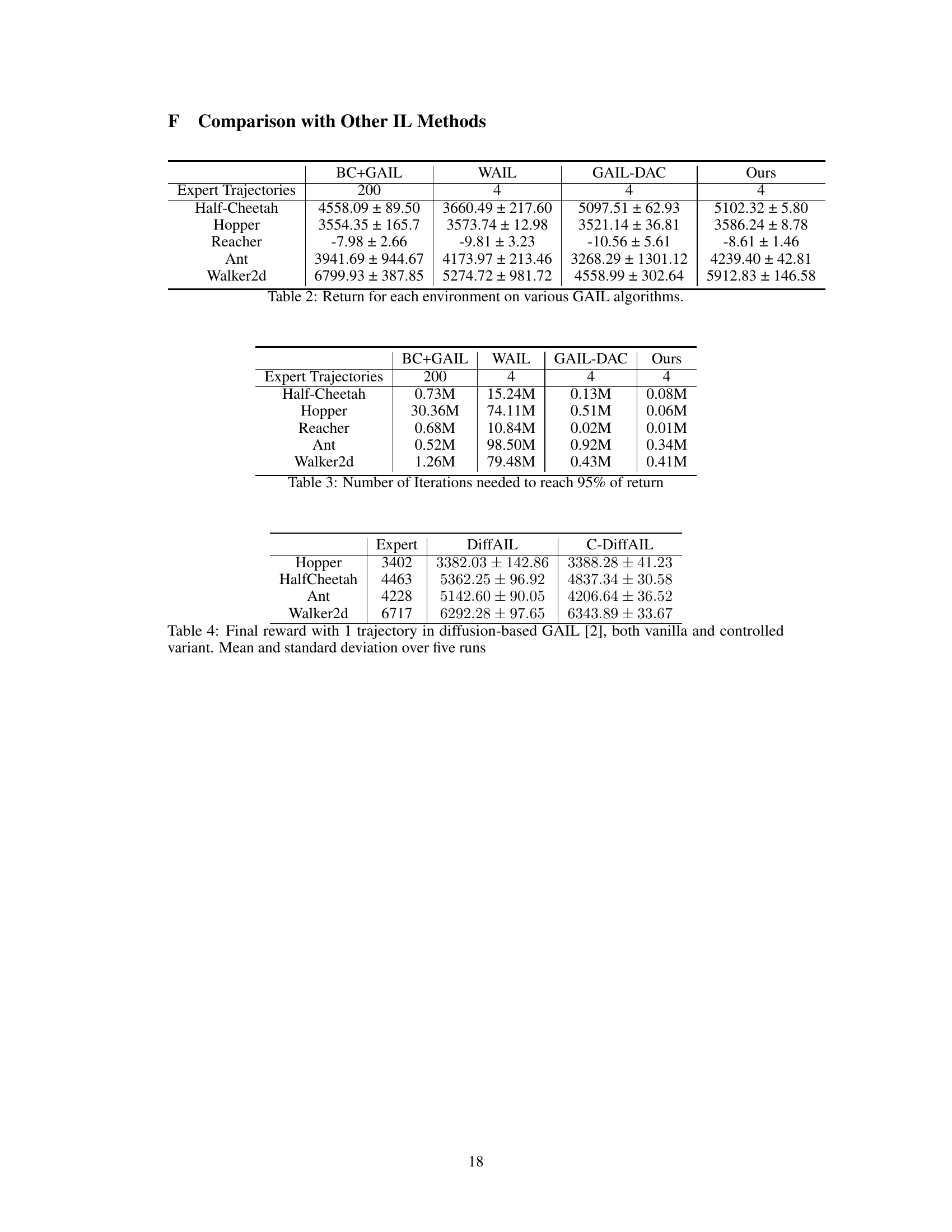
This table presents a comparison of the performance of different imitation learning algorithms, including BC+GAIL, WAIL, GAIL-DAC, and the proposed method (‘Ours’), across five different MuJoCo environments. The results are the average returns achieved by each algorithm, with standard deviations, for each of the five environments. The number of expert trajectories used for training is also specified for each algorithm.

This table shows the number of iterations (in millions) required by different imitation learning methods (BC+GAIL, WAIL, GAIL-DAC, and the proposed C-GAIL) to achieve 95% of the maximum return for five MuJoCo environments (Half-Cheetah, Hopper, Reacher, Ant, and Walker2d). The number of expert trajectories used for training is also specified for each method. The results highlight the efficiency of the proposed C-GAIL in terms of the number of iterations needed to reach near-optimal performance.

This table presents the final reward achieved by three different methods: the expert policy, the vanilla DiffAIL (diffusion-based adversarial imitation learning), and the proposed C-DiffAIL (controlled DiffAIL) method. The results are shown for four different MuJoCo environments (Hopper, HalfCheetah, Ant, and Walker2d). For each environment and method, the mean final reward and its standard deviation across five independent runs are reported. This allows for a comparison of the performance of the proposed C-DiffAIL against the expert and vanilla DiffAIL.

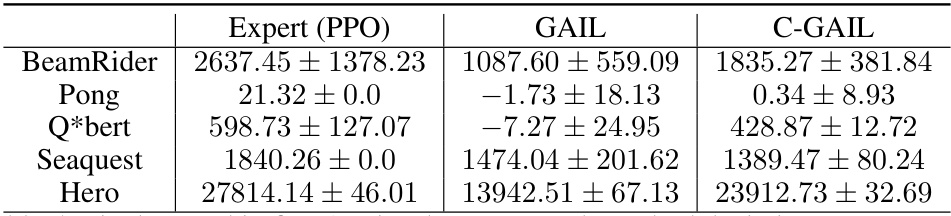
This table presents the final reward achieved by three different methods (Expert PPO, GAIL, and C-GAIL) across five Atari games. For each game, the table shows the mean and standard deviation of the final reward obtained over ten runs of each method. The Expert PPO represents the performance of a well-trained Proximal Policy Optimization (PPO) agent, serving as a benchmark for the imitation learning methods (GAIL and C-GAIL). The results demonstrate the effect of the proposed C-GAIL method on improving the performance of GAIL in Atari games, which are complex environments with high dimensionality.

Full paper

#