↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline reinforcement learning (RL) relies heavily on offline policy evaluation (OPE) to estimate a new policy’s performance using historical data. However, numerous OPE algorithms exist, each with hyperparameters and potential biases, making algorithm selection crucial yet challenging. This necessitates a robust, generalizable approach.
OPERA addresses this issue by combining multiple OPE estimators to produce a single, improved estimate. It employs bootstrapping to estimate the mean squared error of various estimator combinations, optimizing for minimal error. OPERA’s consistency is proven, meaning its estimates improve with more data. Experiments in multiple domains show OPERA consistently outperforms single-estimator and simple averaging approaches, highlighting its practical value for enhancing offline RL systems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in offline reinforcement learning because it offers a novel, general-purpose solution to the problem of estimator selection for policy evaluation. OPERA’s estimator-agnostic approach and proven consistency make it a valuable tool for improving the accuracy and reliability of offline RL systems. This work opens up new avenues for research into meta-learning techniques for combining multiple estimators in other machine learning domains.
Visual Insights#

This figure shows how the weights assigned by OPERA to different estimators are influenced by the bias and variance of those estimators. Four scenarios are presented: * Low bias, differing variance: When both estimators have low bias but one has higher variance, OPERA assigns a higher weight to the estimator with lower variance. * Similar variance, opposite bias: When both estimators have similar variance but opposite biases, OPERA assigns roughly equal weights to both estimators. * High bias, opposite bias: When one estimator is unbiased and the other has high bias, OPERA assigns a weight of 0 to the biased estimator. * Differing bias and variance: When one estimator has low bias and variance and the other has high bias, OPERA assigns a high weight to the low bias/variance estimator and a negative weight to the high bias estimator.
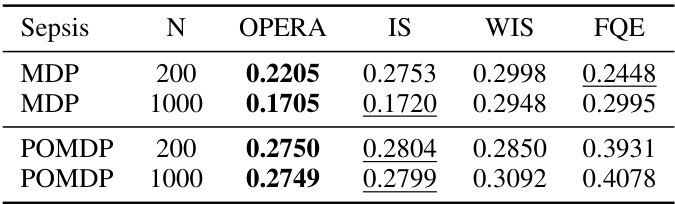
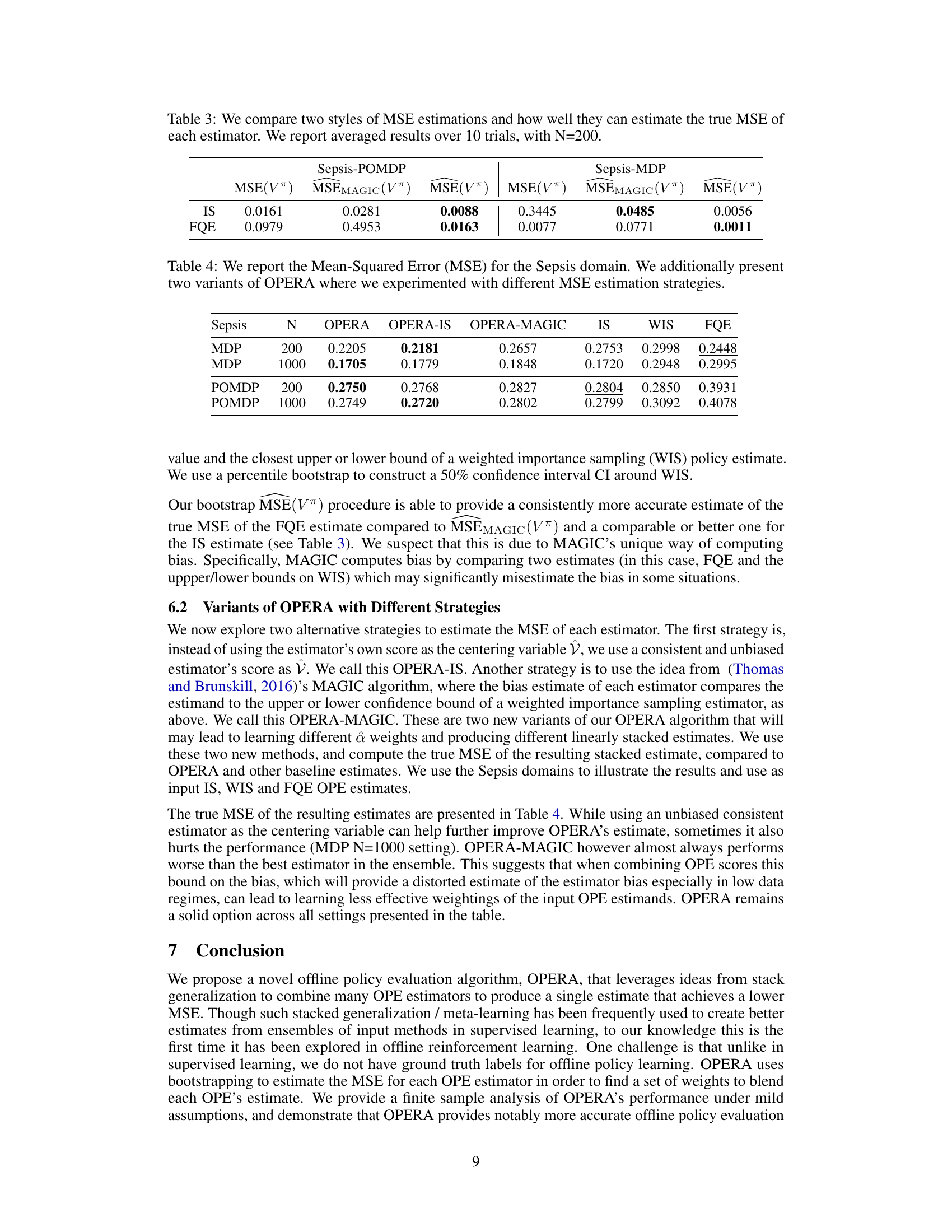
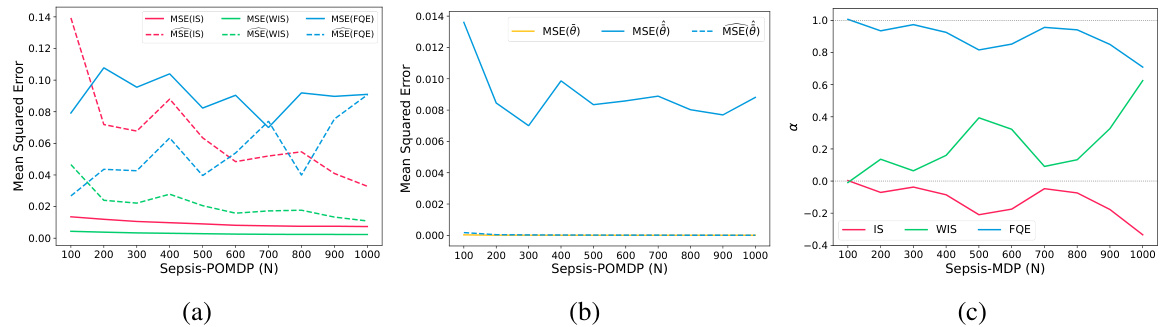
This table shows the mean squared error (MSE) of different offline policy evaluation (OPE) methods on the Sepsis domain, which simulates treatment options for sepsis patients in an ICU. The results are averaged across 20 trials for both MDP and POMDP settings with 200 and 1000 samples. The table compares the performance of OPERA to several other individual OPE methods, such as IS, WIS and FQE, and highlights the best-performing method for each condition by underlining the lowest MSE.
In-depth insights#
OPE Estimator Blend#
Offline Policy Evaluation (OPE) estimator blending is a powerful technique to improve the accuracy and robustness of policy evaluation in reinforcement learning. By combining multiple estimators, each with its strengths and weaknesses, we can mitigate the limitations of individual estimators, such as high variance or bias. The key challenge lies in determining how to effectively combine these estimators. Simple averaging might not be optimal, as some estimators may be more reliable or informative than others. A weighted averaging approach, where weights are assigned based on the estimated quality or reliability of each estimator, could offer significant advantages. However, estimating these weights reliably can be difficult, and sophisticated methods, like bootstrapping, may be necessary. The choice of blending technique depends heavily on the characteristics of the estimators and the data, requiring careful consideration of bias-variance tradeoffs. Ultimately, the success of OPE estimator blending hinges on choosing a robust and appropriate aggregation strategy, potentially incorporating adaptive weighting or model selection mechanisms. This is a rich and active research area with significant potential to enhance the reliability and efficacy of offline reinforcement learning.
OPERA Algorithm#
The OPERA algorithm presents a novel approach to offline policy evaluation by intelligently combining multiple estimators. Its strength lies in its estimator-agnostic nature, allowing for the integration of diverse methods without requiring specific assumptions about their characteristics. The algorithm leverages a weighted averaging scheme, where weights are learned via a constrained optimization problem that minimizes the mean squared error. This optimization is particularly innovative because it utilizes bootstrapping to effectively estimate the MSE, avoiding reliance on unavailable ground truth values. The resulting combined estimator often outperforms individual estimators, especially in low data regimes. Further, OPERA offers valuable interpretability through its weights, revealing insights into the relative importance and quality of each component estimator. However, it’s crucial to note that the performance of OPERA is contingent on the underlying estimators used and its accuracy might be limited by the inherent biases and variability present in the input data.
Bootstrapping MSE#
The concept of “Bootstrapping MSE” involves using the bootstrap method, a resampling technique, to estimate the mean squared error (MSE) of an estimator. This is particularly valuable in offline policy evaluation (OPE) where ground truth isn’t readily available, making traditional MSE calculation impossible. The core idea is to create multiple bootstrap samples from the original dataset, apply the estimator to each, and then calculate the MSE across these bootstrapped estimates. This provides a robust and data-driven way to gauge an estimator’s accuracy without relying on assumptions about the underlying data distribution. A key advantage is its applicability to diverse OPE estimators, not needing to calculate theoretical variances or biases. However, bootstrapping MSE introduces computational overhead due to repeated estimator evaluations on resampled datasets and accuracy depends heavily on the sample size and smoothness of the estimators. The choice of bootstrap parameters like resample size also affects the accuracy of the MSE estimate. Consequently, careful consideration of these tradeoffs is needed for reliable OPE using this technique.
Offline RL domains#
Offline reinforcement learning (RL) presents unique challenges due to its reliance on logged historical data, rather than live interaction. The choice of offline RL domains significantly impacts the success and applicability of algorithms. Domains with diverse characteristics, such as high dimensionality, complex dynamics, and sparse rewards, necessitate careful consideration of the data quality, bias, and representativeness. Domains like robotics control demand high-precision, safe policies, which are challenging to learn offline without extensive testing. Healthcare settings pose ethical considerations, requiring careful handling of patient data and responsible policy deployment to avoid negative consequences. Simpler domains, such as contextual bandits or simulated environments, can serve as valuable testbeds for developing and evaluating new algorithms, but may not generalize well to more complex, real-world scenarios. The transferability of insights and algorithms across different offline RL domains remains a significant challenge. Thus, thorough analysis of domain-specific characteristics is critical for the robust development and reliable evaluation of offline RL techniques.
OPERA limitations#
The OPERA algorithm, while innovative in its approach to offline policy evaluation, has limitations. Its reliance on bootstrapping to estimate the mean squared error (MSE) introduces variance and potential bias, especially with smaller datasets. The consistency of OPERA depends on the underlying OPE estimators’ quality; if the base estimators are poor, OPERA’s performance will suffer despite its ability to optimally combine them. The linear weighted averaging of the estimators’ outputs may not adequately capture complex relationships between them, leading to suboptimal results in situations where non-linear combinations would be more appropriate. Furthermore, the computational cost of OPERA can scale significantly with the number of estimators, potentially hindering scalability to large-scale problems. The algorithm’s interpretability is limited despite the information provided by the weights; gaining deeper insights into why OPERA chooses certain weights over others is not straightforward. Finally, assumptions about the smoothness and boundedness of the estimators are required for theoretical guarantees, limitations that may not always hold in practice.
More visual insights#
More on figures
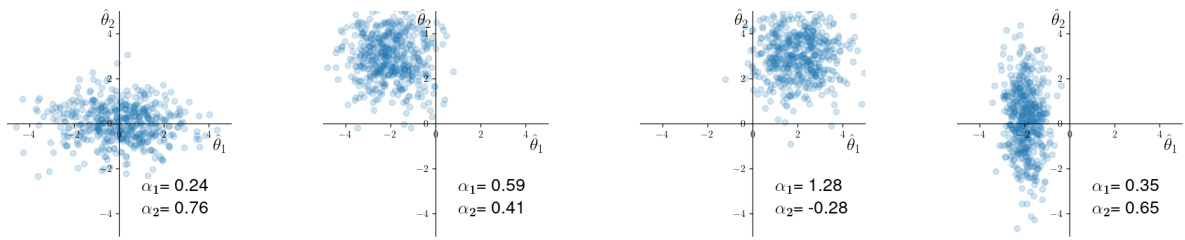
This figure shows how OPERA assigns weights to different estimators based on their bias and variance. Each subplot represents a different scenario with two estimators (V₁ and V₂). The x-axis shows the value of V₁, and the y-axis shows the value of V₂. The assigned weights (α₁ and α₂) are indicated in each subplot. The plots demonstrate how OPERA adjusts weights to leverage the strengths of low-variance, low-bias estimators, handle opposing biases, and account for variations in estimator properties.
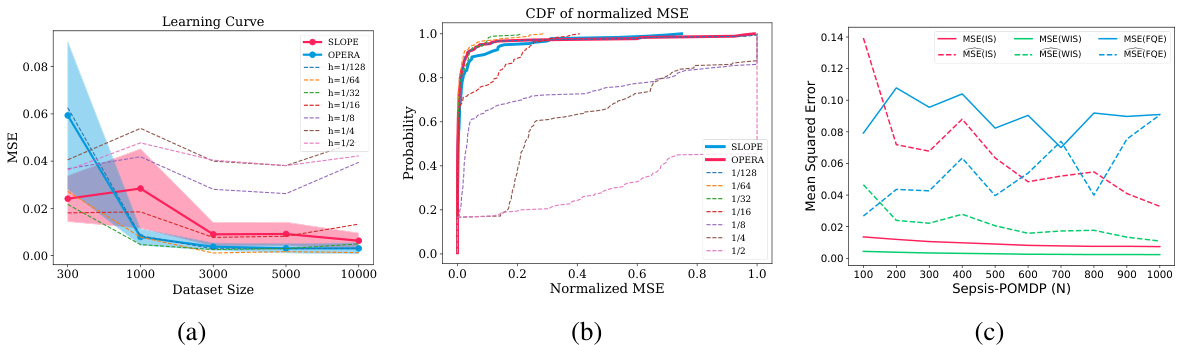
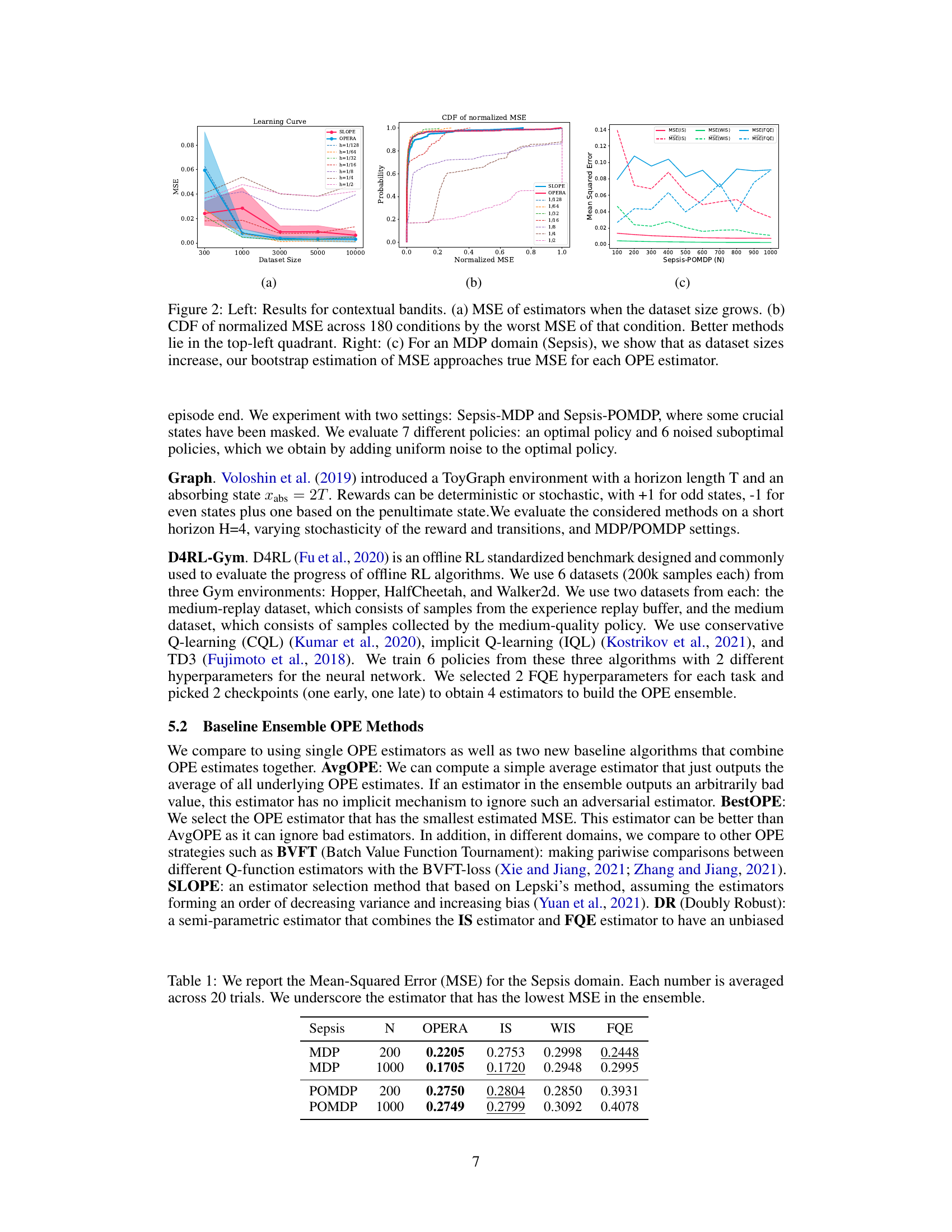
This figure shows the results of contextual bandit and sepsis experiments. The left side shows the mean squared error (MSE) of different estimators as the dataset size grows for contextual bandits. It also presents a cumulative distribution function (CDF) of normalized MSE, allowing for comparison across various conditions. The right side focuses on the Sepsis domain, demonstrating how the bootstrap estimation of MSE converges to the true MSE for each Offline Policy Evaluation (OPE) estimator as the dataset size increases.
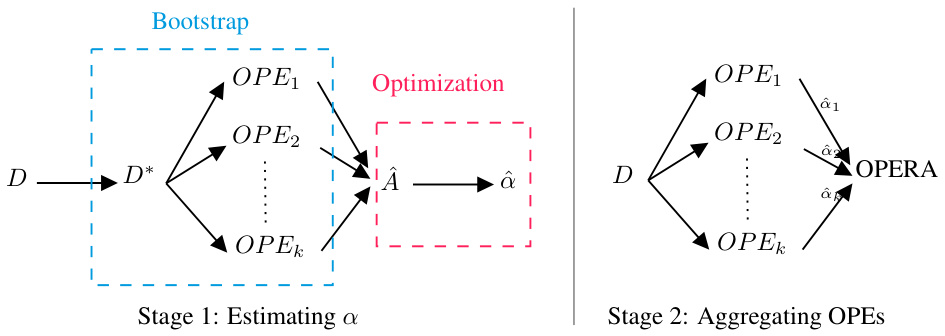
The figure illustrates the OPERA framework as a two-stage process. Stage 1 involves using bootstrap to estimate the quality of each OPE estimator, and then using this information to estimate a weight vector ( \hat{\alpha} ) through convex optimization. Stage 2 uses the learned weight vector to combine each estimator’s score, resulting in the OPERA score. The diagram visually represents the flow of data and computations in the OPERA algorithm.
This figure shows how OPERA assigns weights to different estimators based on their bias and variance. The plots illustrate different scenarios: when estimators have low bias but different variances, OPERA favors the estimator with lower variance; when estimators have similar variance but opposite biases, OPERA assigns weights that approximately cancel out the biases; and when one estimator is unbiased and the other has low variance, OPERA assigns weights inversely proportional to their MSE contributions.
More on tables

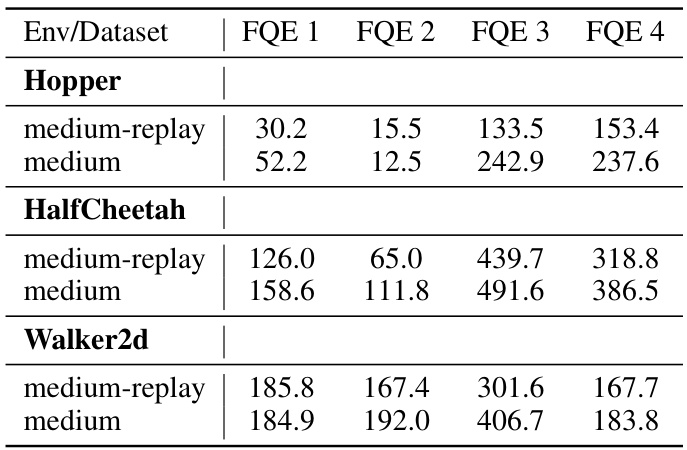
This table presents the Root Mean Squared Error (RMSE) results for various Offline Policy Evaluation (OPE) algorithms across different D4RL (Datasets for Deep Data-driven Reinforcement Learning) tasks. The tasks are categorized by environment (Hopper, HalfCheetah, Walker2d) and dataset type (medium-replay, medium). The table compares the performance of OPERA against several single OPE estimators and other multi-OPE estimators including BestOPE, AvgOPE, BVFT, DR, and Dual-DICE. Lower RMSE values indicate better performance.

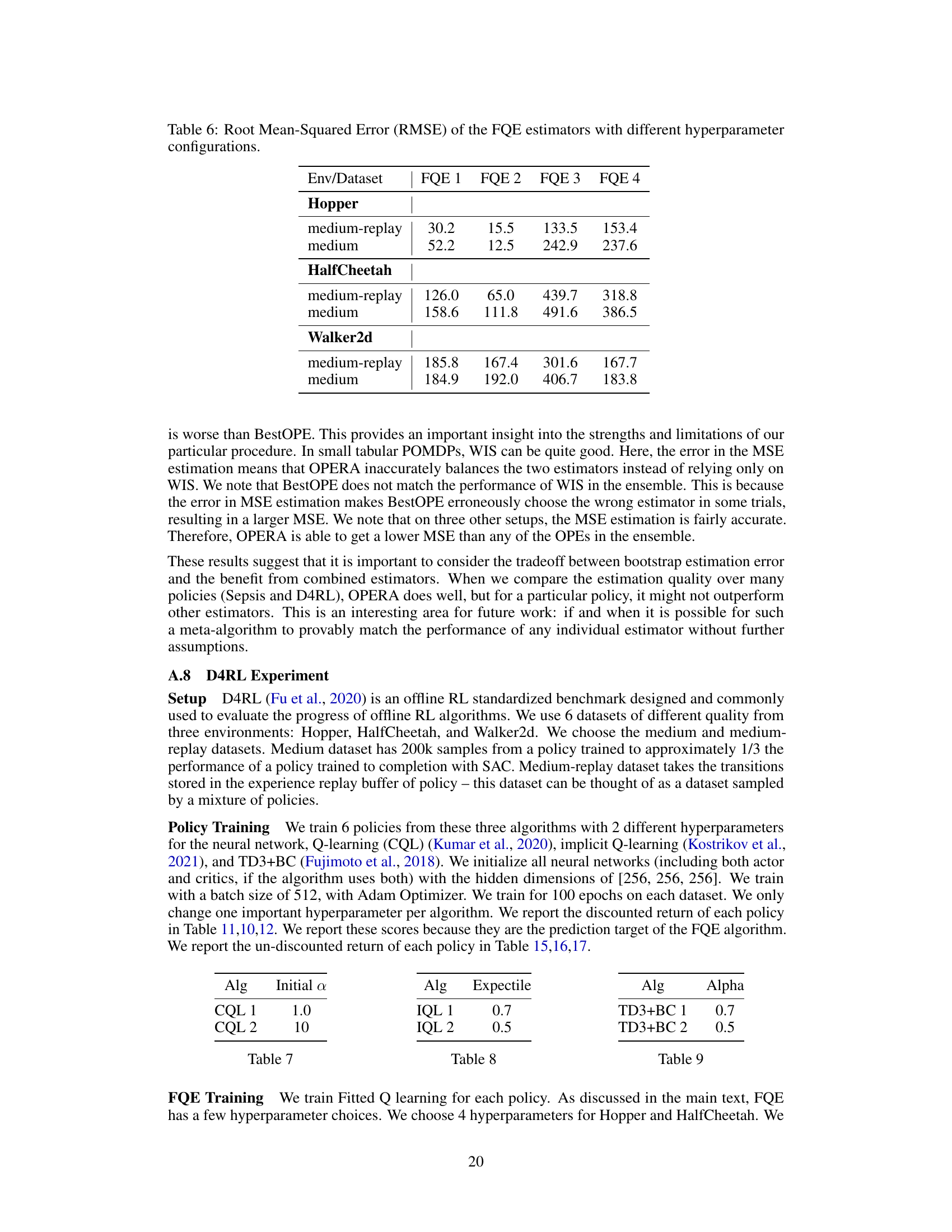
This table compares two methods for estimating the mean squared error (MSE) of offline policy evaluation (OPE) estimators: the proposed bootstrapping method and the MAGIC method. It shows the estimated MSEs for two estimators (IS and FQE) under two different scenarios (Sepsis-POMDP and Sepsis-MDP) with a sample size of N=200. The results indicate the accuracy of each MSE estimation method in approximating the true MSE values.
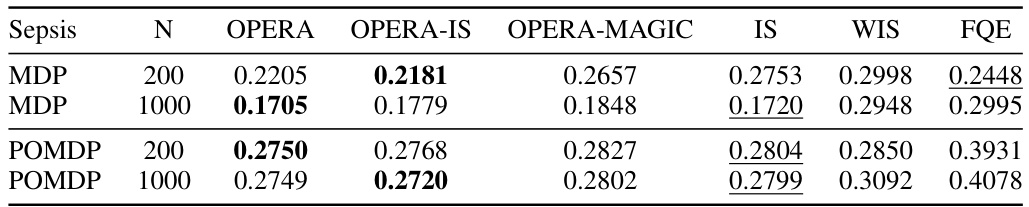
This table shows the mean squared error (MSE) for different offline policy evaluation (OPE) estimators on the Sepsis domain. The MSE is calculated for four different OPE methods (IS, WIS, FQE) and three variants of the OPERA algorithm (OPERA, OPERA-IS, OPERA-MAGIC). The results are averaged over 20 trials and different dataset sizes (200 and 1000 samples). The lowest MSE for each setting is highlighted.

This table presents the root mean squared error (RMSE) of various offline policy evaluation (OPE) algorithms across different tasks within the D4RL benchmark. It compares the performance of OPERA against single OPE estimators (IS, WIS, FQE, MB, DR, Dual-DICE) and other ensemble methods (AvgOPE, BestOPE, BVFT). The results are categorized by environment (Hopper, HalfCheetah, Walker2D) and dataset type (medium-replay, medium). Lower RMSE values indicate better performance.

This table presents the mean squared error (MSE) for different offline policy evaluation (OPE) estimators on the ToyGraph environment. The experiment was conducted 10 times with various settings for stochasticity, observability (MDP vs. POMDP), and the choice of OPE estimator (OPERA, BestOPE, AvgOPE, IS, WIS). The lowest MSE for each setting is underscored, highlighting OPERA’s performance relative to other methods.
This table presents the Root Mean Squared Error (RMSE) for different offline policy evaluation (OPE) algorithms across multiple tasks from the D4RL benchmark. The benchmark includes tasks from various robotics domains such as Hopper, HalfCheetah, and Walker2d, with each task having ‘medium-replay’ and ‘medium’ datasets, representing different data collection scenarios. Algorithms are compared to OPERA using the ‘BestOPE’, ‘AvgOPE’, ‘BVFT’, ‘DR’, and ‘Dual-DICE’ methods, allowing for a comprehensive comparison of their performance across diverse scenarios and datasets. The lower the RMSE, the better the algorithm’s performance in estimating the policy’s value.

This table shows the mean squared error (MSE) of different offline policy evaluation (OPE) estimators on the Sepsis domain. The results are averaged across 20 trials, and the lowest MSE for each setting is indicated by underlining. The table compares the performance of different OPE methods, including importance sampling (IS), weighted importance sampling (WIS), fitted Q-evaluation (FQE) and OPERA, demonstrating OPERA’s improved accuracy in offline policy evaluation compared to other methods.

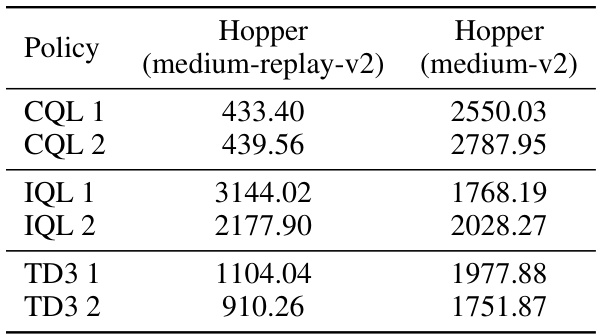
This table presents the discounted performance results for six different policies on the Hopper task, categorized by the dataset used (medium-replay and medium). The policies evaluated include two versions each of CQL, IQL, and TD3+BC, representing different hyperparameter configurations for each algorithm. The values likely represent an average discounted cumulative reward, reflecting the algorithm’s performance in achieving a specific goal within the simulation.

This table presents the discounted performance results for different policies evaluated on the Hopper task. The table shows the discounted reward obtained by each of six different policies on the Hopper task, categorized by the type of dataset used (medium-replay or medium). These results likely represent a subset of the overall findings, used to illustrate the performance of the OPERA algorithm in a specific context.

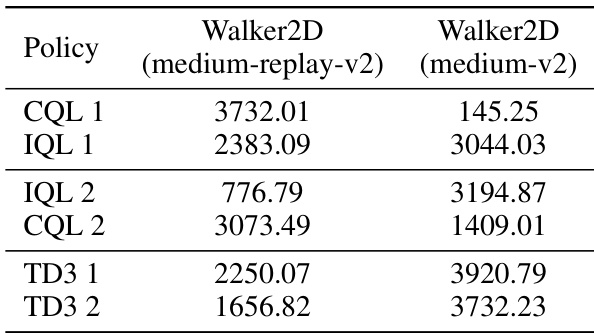
This table presents the discounted performance of six different policies on the HalfCheetah task from the D4RL benchmark. The policies were trained using three different algorithms (CQL, IQL, TD3+BC) with two hyperparameter settings each. The ‘medium-replay’ and ‘medium’ columns indicate the dataset used for training. Discounted reward is a common metric in reinforcement learning, reflecting the cumulative reward over time, discounted by a factor to emphasize near-term rewards.
This table presents the Mean Squared Error (MSE) for different offline policy evaluation (OPE) estimators on the Sepsis domain. The results are averaged over 20 trials for both MDP and POMDP settings with varying dataset sizes (N=200 and N=1000). The estimator with the lowest MSE in each case is underscored, highlighting OPERA’s performance in comparison to other methods (IS, WIS, FQE).
This table presents the Root Mean Squared Error (RMSE) achieved by different Offline Policy Evaluation (OPE) algorithms on various D4RL tasks. D4RL is a standardized benchmark for offline RL, and the tasks represent different robotics control problems with varying data characteristics. The algorithms compared include OPERA (the proposed method), along with baseline methods like AvgOPE (average OPE), BestOPE (best-performing OPE), BVFT (Batch Value Function Tournament), DR (doubly robust), Dual-DICE, and MB (model-based). The results show the RMSE across different datasets (‘medium’ and ‘medium-replay’) for three environments: Hopper, HalfCheetah, and Walker2d.
The table presents the Root Mean Squared Error (RMSE) for different offline policy evaluation (OPE) algorithms across various tasks within the D4RL benchmark. It compares OPERA’s performance against several single OPE estimators and other ensemble methods. The results show RMSE values for different D4RL environments (Hopper, HalfCheetah, Walker2d) and datasets (medium-replay, medium) providing a comprehensive comparison of the algorithms’ accuracy in offline RL.
The table presents the Root Mean Squared Error (RMSE) of different Offline Policy Evaluation (OPE) algorithms across various D4RL (Datasets for Deep Data-driven Reinforcement Learning) tasks. It compares OPERA’s performance against several baseline methods (BestOPE, AvgOPE, BVFT, DR, Dual-DICE, MB) for different environments and datasets (medium-replay and medium). Lower RMSE values indicate better performance.
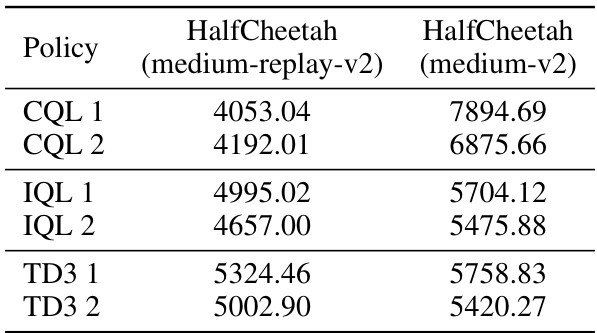
This table presents the undiscounted performance results for different policies on the HalfCheetah task, categorized by the dataset used (medium-replay-v2 and medium-v2). Each row represents a different policy (CQL 1, CQL 2, IQL 1, IQL 2, TD3 1, and TD3 2), and the columns show the undiscounted performance metrics for each policy on the specified datasets.
Full paper#