Federated Online Prediction from Experts with Differential Privacy: Separations and Regret Speed-ups

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it bridges the gap between federated learning and differential privacy, two significant research areas. It offers novel algorithms and theoretical analyses, providing valuable insights into the challenges and possibilities of private collaborative learning. The findings can significantly advance the development of privacy-preserving machine learning systems and inspire future research in this rapidly evolving field.

Visual Insights

#

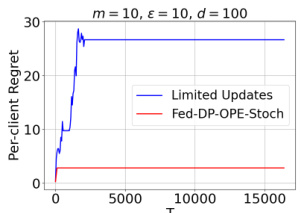
The figure compares the per-client regret of the Fed-DP-OPE-Stoch algorithm and the Limited Updates algorithm as a function of the time horizon T. The plot shows that Fed-DP-OPE-Stoch achieves significantly lower regret than Limited Updates, demonstrating the effectiveness of the proposed federated learning approach. The experiment used parameters m=10, ε=10, and d=100.

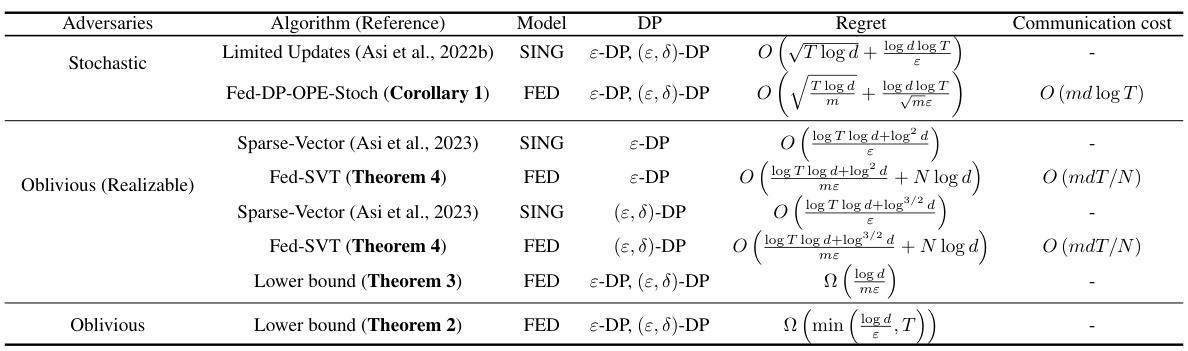
This table compares the regret and communication cost of different algorithms for online prediction from experts under various differential privacy constraints. It contrasts single-client and federated settings for both stochastic and oblivious adversaries, highlighting the impact of collaboration and privacy mechanisms on the performance of the algorithms. The table also includes lower bounds to benchmark the optimality of the proposed algorithms.

In-depth insights

#

Fed-OPE: DP Speedups

#

The heading ‘Fed-OPE: DP Speedups’ suggests a research focus on improving the efficiency of Federated Online Prediction (Fed-OPE) while incorporating Differential Privacy (DP). The core idea is likely to explore algorithmic techniques that reduce the regret (a measure of performance in online learning) in a federated setting. The ‘DP’ component highlights the crucial aspect of preserving data privacy during the collaborative learning process. The ‘Speedups’ indicate that the research aims to achieve faster convergence or improved efficiency compared to traditional Fed-OPE methods. This likely involves developing novel algorithms that leverage the distributed nature of federated learning while effectively managing the privacy-preserving noise that DP mandates. Successful speedups would demonstrate a significant advancement, allowing for faster model training in privacy-sensitive applications.

Stochastic Adversary

#

In the context of online prediction from experts, a stochastic adversary represents a probabilistic model of an opponent’s actions. Unlike an oblivious adversary that pre-determines its loss function sequence, the stochastic adversary samples loss functions from a fixed distribution at each time step, independently and identically. This probabilistic nature introduces an element of randomness into the learning process, making it more challenging and realistic to model real-world scenarios. Algorithms designed to handle stochastic adversaries must incorporate this uncertainty, usually employing strategies to estimate loss function distributions or to adapt to changing environments. The design of differentially private algorithms for this scenario often involves careful noise-adding mechanisms that still provide utility despite this randomness. Federated learning, where multiple clients collaborate, introduces additional complexities with stochastic adversaries. However, as the paper showcases, it also offers opportunities to improve efficiency and reduce the regret by means of better gradient estimations and aggregated noise, leading to a potential speedup over single-client counterparts.

Oblivious Adversary

#

The concept of an oblivious adversary presents a significant challenge in online learning, particularly within the context of federated settings. Unlike stochastic adversaries, which draw loss functions from a known distribution, an oblivious adversary strategically selects loss functions beforehand, rendering traditional collaborative strategies less effective. The paper highlights a crucial separation between stochastic and oblivious adversaries in federated online prediction. While collaboration among clients offers a speedup in the stochastic setting, lower bounds are established demonstrating the lack of such benefits in the general oblivious adversary case. This suggests that the inherent unpredictability of an oblivious adversary negates the advantages of data aggregation and collaboration in federated learning. However, a notable exception is identified when a low-loss expert exists. Under this realizability assumption, a new algorithm demonstrates a significant speedup. This highlights a fundamental distinction: collaboration is beneficial only under specific conditions when facing an oblivious adversary. The findings emphasize the importance of considering adversary types when designing federated online learning systems and selecting appropriate collaborative strategies.

Realizable Setting

#

The concept of a ‘realizable setting’ in online learning signifies a scenario where perfect prediction is attainable. This typically involves the existence of an expert (or model) that consistently achieves zero loss. In a federated learning context with oblivious adversaries, this assumption is particularly significant because it mitigates the challenge posed by adversaries who can arbitrarily select loss functions. With the ‘realizable setting’, collaboration among clients becomes far more advantageous. The shared goal of identifying this perfect expert allows for a significant speed-up in the learning process, reducing the overall regret, which is the cumulative difference between the algorithm’s performance and the optimal expert’s performance. This speed-up is a key focus of research in this area, and the ‘realizable setting’ is used to demonstrate the benefits of collaboration in a situation where it’s less intuitive due to the presence of oblivious adversaries. Establishing lower bounds in this setting helps to demonstrate the near optimality of proposed algorithms.

Future of Fed-OPE

#

The future of Federated Online Prediction from Experts (Fed-OPE) is bright, particularly given its potential for improving numerous applications. Privacy-preserving collaborative learning is key, with continued research into advanced differential privacy mechanisms crucial for ensuring data confidentiality while maximizing the benefits of distributed data. Further exploration of different adversary models beyond stochastic and oblivious is needed to make Fed-OPE more robust in real-world scenarios. Algorithm development should focus on minimizing communication overhead and improving efficiency, perhaps through techniques like quantization and sparsification. Finally, real-world applications need more attention to test and refine the algorithms. Areas like healthcare, finance, and personalized recommendations offer significant opportunities for impactful Fed-OPE implementations, though careful consideration of ethical implications will be paramount.

More visual insights

#

More on figures

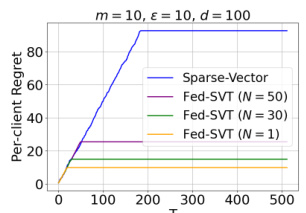
The figure shows the per-client regret as a function of the time horizon (T) for different algorithms. The algorithms compared are Sparse-Vector (a single-player model), and Fed-SVT (the federated algorithm proposed in the paper) with different communication intervals (N). The results indicate that Fed-SVT outperforms the single-player model significantly, highlighting the benefits of collaborative expert selection in reducing the per-client regret, even with infrequent communication.

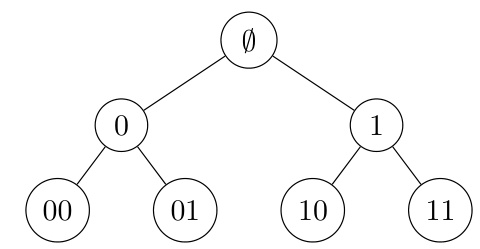
This figure shows a binary tree structure used in the DP-FW algorithm (Algorithm 3). The root node is labeled Ø, representing the initial gradient estimate. Each internal node represents an intermediate gradient estimate calculated from its child nodes. The leaf nodes represent final gradient estimates calculated using the DP-FW algorithm’s iterative process on sets of loss functions assigned to each leaf. The tree’s structure determines the hierarchical gradient aggregation in the algorithm, enabling privacy-preserving estimation.

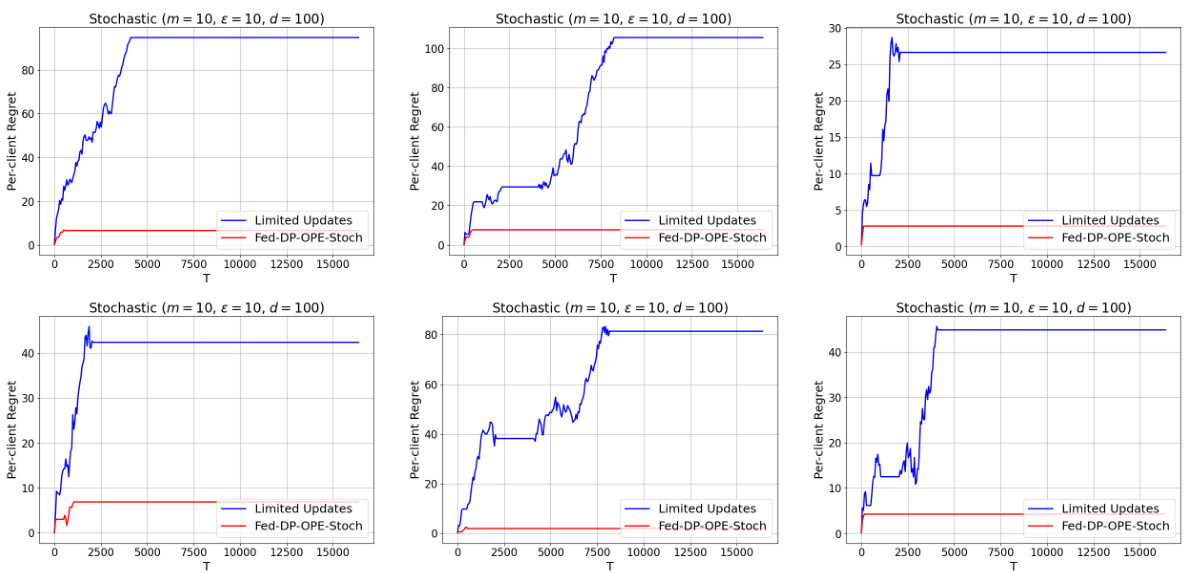
The figure compares the performance of the Fed-DP-OPE-Stoch algorithm and the Limited Updates algorithm, both designed for online prediction from experts under differential privacy constraints with stochastic adversaries. The experiment is repeated six times with different random seeds to demonstrate the consistency and robustness of the results. Each subplot shows the per-client cumulative regret as a function of time horizon (T) for one experiment with different random seeds. The results show that Fed-DP-OPE-Stoch consistently outperforms Limited Updates, illustrating its effectiveness and the benefits of the proposed federated approach.

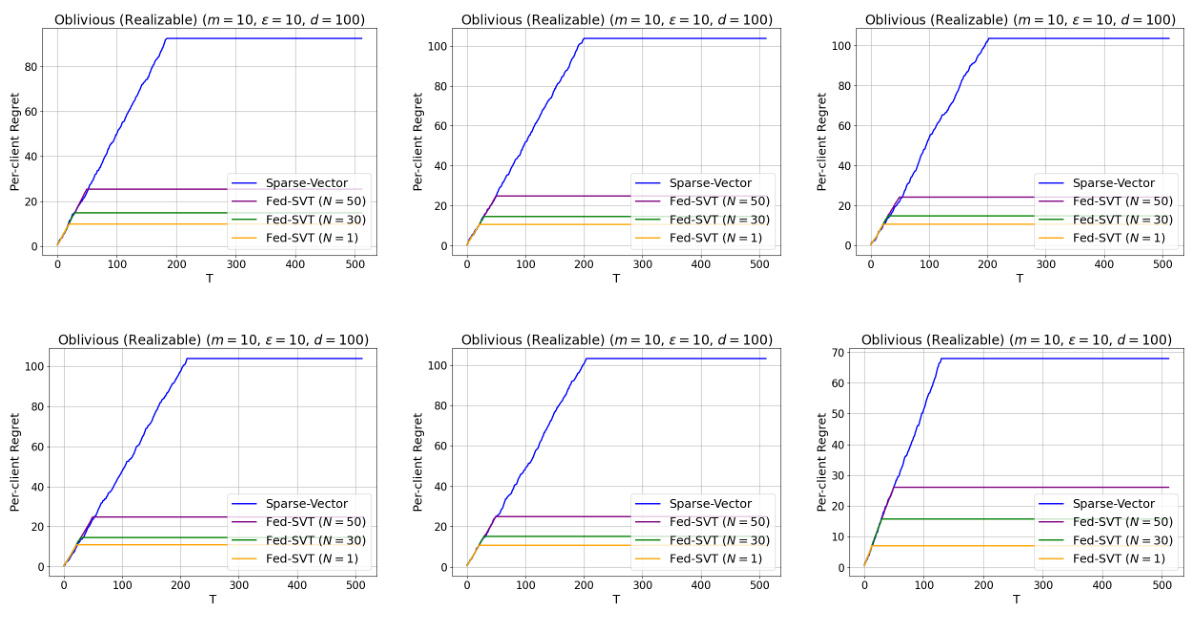
This figure compares the performance of the proposed Fed-SVT algorithm against the Sparse-Vector algorithm, a single-player baseline, under different random seeds for an oblivious realizable setting. It demonstrates the impact of varying communication intervals (N = 1, 30, 50) on the per-client regret of Fed-SVT. The results visually showcase the significant reduction in regret achieved by Fed-SVT compared to Sparse-Vector, highlighting the benefits of collaborative learning in the realizable scenario.

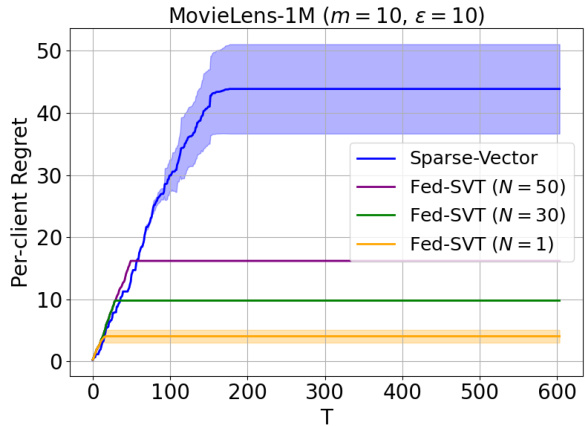
This figure compares the performance of the Fed-SVT algorithm with different communication intervals (N = 1, 30, 50) against the Sparse-Vector algorithm on the MovieLens-1M dataset. The y-axis represents the per-client regret, and the x-axis represents the time horizon (T). The shaded area represents the standard deviation across multiple runs. The results demonstrate that Fed-SVT, especially with larger communication intervals, achieves significantly lower regret than Sparse-Vector.

Full paper

#