↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current video violence detection (VVD) methods primarily use Euclidean space representation learning, but struggle to discriminate between visually similar events (like ambiguous violence). Hyperbolic representation learning, adept at capturing hierarchical relationships, offers a potential solution, but existing approaches have limitations in feature extraction and information aggregation.
The researchers developed Dual-Space Representation Learning (DSRL) that combines the strengths of both Euclidean and hyperbolic spaces. DSRL uses a novel Hyperbolic Energy-constrained Graph Convolutional Network (HE-GCN) with a layer-sensitive hyperbolic association degree for effective message passing in hyperbolic space. Furthermore, a Dual-Space Interaction (DSI) module leverages cross-space attention for effective information interaction between the two spaces. Experiments show DSRL outperforms existing methods, especially in detecting ambiguous violence, demonstrating the effectiveness of this dual-space approach.
Key Takeaways#
Why does it matter?#
This paper is crucial because it introduces a novel Dual-Space Representation Learning (DSRL) method for weakly supervised video violence detection. This addresses a critical limitation of existing methods that struggle with ambiguous violence, opening avenues for more robust and accurate violence detection systems. Its innovative approach of combining Euclidean and hyperbolic geometries for enhanced feature learning offers significant potential in other computer vision tasks involving complex hierarchical relationships.
Visual Insights#

The figure is composed of two parts: (a) shows a hierarchical diagram of video violence detection, illustrating the hierarchical structure of event categories (violent vs. normal events) and event development (before, during, and after a violent event); (b) illustrates the proposed Dual-Space Representation Learning (DSRL) method, highlighting its ability to improve ambiguous violence detection by combining the strengths of both Euclidean and hyperbolic spaces, which captures visual features and hierarchical relationships between events respectively.
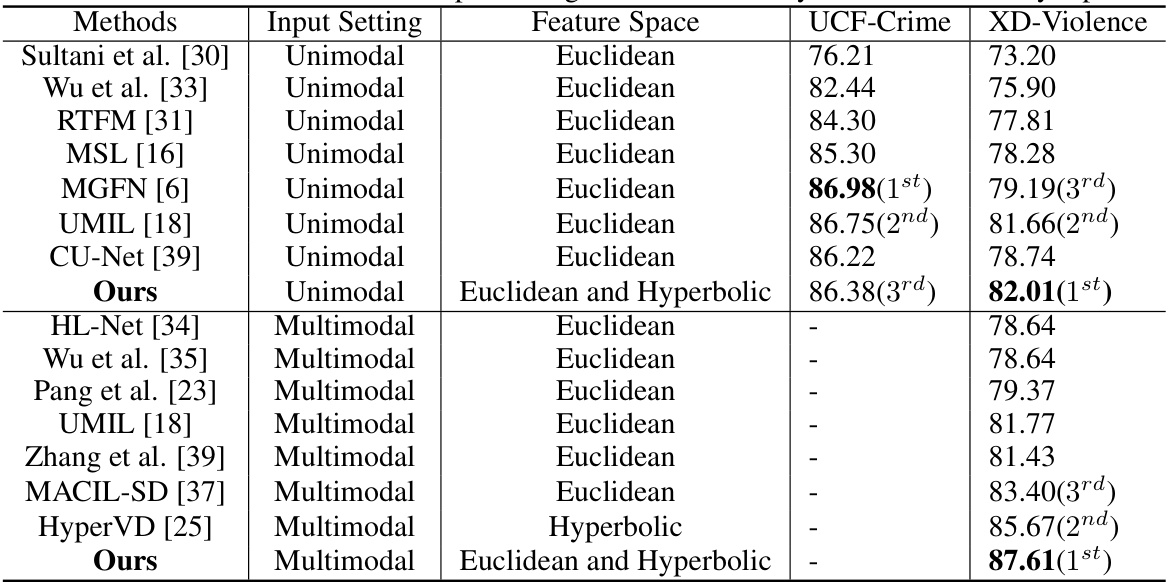
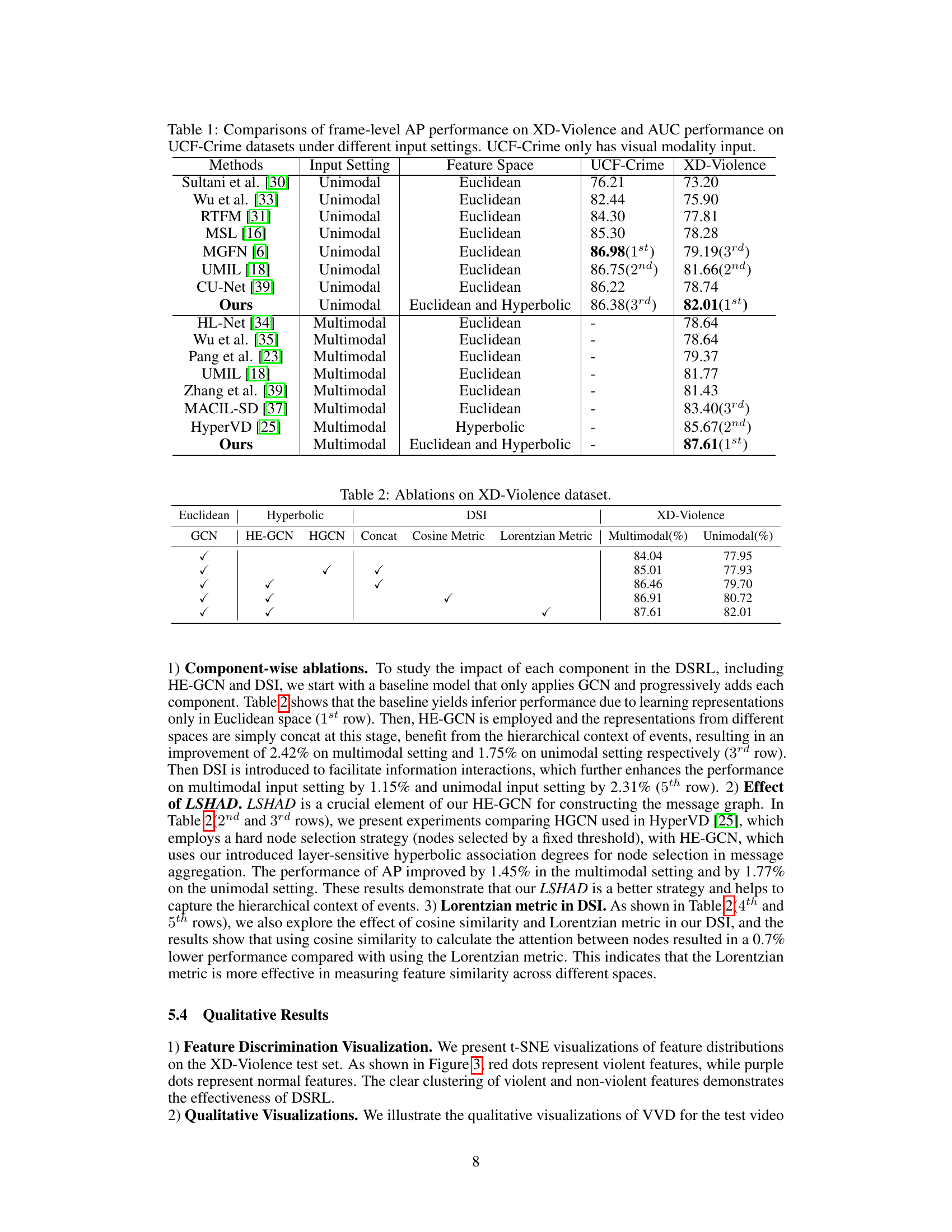
This table compares the performance of different methods on two video violence detection datasets: XD-Violence (multimodal) and UCF-Crime (unimodal). It shows the average precision (AP) for XD-Violence and the area under the curve (AUC) for UCF-Crime, highlighting the performance differences across various methods and input modalities (unimodal vs. multimodal). The table also specifies each method’s utilized feature space (Euclidean, hyperbolic, or both).
In-depth insights#
Beyond Euclidean VVD#
The heading ‘Beyond Euclidean VVD’ suggests a departure from traditional Euclidean geometry-based approaches in video violence detection (VVD). Euclidean methods often struggle with the nuances of visual data, particularly in distinguishing between similar-looking violent and non-violent events. This research likely explores alternative geometric spaces, such as hyperbolic space, to better capture the hierarchical and complex relationships within video data. Hyperbolic geometry excels at modeling hierarchical structures, potentially improving the discrimination between visually similar events. This approach might involve representing video frames as points in a hyperbolic space, where the distance between points reflects the semantic similarity of the corresponding events. The ‘Beyond Euclidean’ aspect likely involves integrating both Euclidean and hyperbolic representations, leveraging the strengths of each space. Euclidean space captures low-level visual features, while hyperbolic space models higher-level semantic relationships. Combining these may provide a more robust and comprehensive representation for VVD, leading to improved accuracy and better handling of ambiguous situations.
Dual-Space Learning#
Dual-space learning, as a novel approach, cleverly combines the strengths of Euclidean and hyperbolic geometries for enhanced feature representation. Euclidean space excels at capturing fine-grained visual details, while hyperbolic space is adept at modeling hierarchical relationships and complex structures, often found in events like violence detection. This dual approach is particularly beneficial when dealing with ambiguous events, where subtle differences in context or visual similarity can lead to misclassifications. By integrating both spaces, dual-space learning effectively leverages the discrimination power of Euclidean features while enriching the representations with the contextual understanding afforded by hyperbolic geometry. The result is a more robust and accurate model, capable of handling complex scenarios with improved precision and recall. Cross-space attention further refines the process, allowing for seamless interaction and information exchange between the two spaces, resulting in a more comprehensive and discriminative final representation that leads to better performance in video violence detection or similar tasks.
Hyperbolic Geometry#
Hyperbolic geometry, unlike Euclidean geometry, is characterized by a constant negative curvature, leading to properties that make it suitable for modeling hierarchical relationships and complex structures. This non-Euclidean space offers advantages in machine learning because it can effectively represent data with inherent hierarchical structures, where distances between points increase exponentially as they move apart. Hyperbolic spaces naturally capture hierarchical relationships found in many datasets, providing a more accurate representation than Euclidean space which often struggles with high dimensionality and complex interdependencies. The use of hyperbolic geometry in the paper presents a novel way to handle the inherent hierarchical nature of event relationships in video data. By leveraging hyperbolic representation learning, the researchers aim to improve the discriminative capability of their video violence detection model, especially when dealing with ambiguous scenarios that look similar to violent events. This is because the hierarchical modeling capacity of hyperbolic geometry allows for a more nuanced understanding of the relationships between different types of events, thereby improving classification accuracy.
Cross-Space Attention#
The concept of ‘Cross-Space Attention’ in the context of a research paper focusing on video violence detection using dual-space representation learning is quite intriguing. It suggests a mechanism that bridges the gap between Euclidean and hyperbolic spaces, allowing information to flow bidirectionally between the two. The Euclidean space likely captures low-level visual features like motion and object appearance, while the hyperbolic space might model the hierarchical relationships and temporal context of events. Cross-space attention, therefore, would enable the model to leverage the strengths of both representations. For example, high-level contextual information from the hyperbolic space could guide the attention in the Euclidean space, highlighting visually salient features relevant to violence. Similarly, strong visual cues in Euclidean space could reinforce or refine the hierarchical understanding in hyperbolic space. This cross-interaction is crucial because relying solely on one space may lead to incomplete or inaccurate violence detection. Ambiguous events, which look similar to both normal and violent scenarios, are particularly susceptible to improved analysis through this technique. The effectiveness of this approach hinges on the design of the attention mechanism itself, requiring careful consideration of distance metrics and appropriate weight assignment for interactions between spaces. The success depends on how well the attention mechanism effectively fuses the complementary information from both spaces, creating a more robust and accurate representation for violence detection.
Future of VVD#
The future of Video Violence Detection (VVD) hinges on addressing current limitations and leveraging emerging technologies. Improving the accuracy of VVD in ambiguous scenarios remains crucial, necessitating more robust feature extraction and representation learning techniques that can distinguish between visually similar violent and non-violent events. Multimodal approaches, incorporating audio and other contextual information, are likely to enhance accuracy and robustness. Advances in deep learning architectures and training methodologies will continue to play a vital role, potentially improving the efficiency and scalability of VVD systems. Furthermore, the development of larger, more diverse, and meticulously annotated datasets is essential to train more generalizable and reliable models. Addressing ethical concerns surrounding privacy and bias in VVD systems will also be paramount, necessitating careful consideration of data collection and model deployment strategies. Finally, real-time and resource-efficient VVD solutions are highly desirable for practical applications, especially in surveillance and security contexts, driving further research into optimized algorithms and hardware acceleration techniques.
More visual insights#
More on figures

The figure demonstrates the advantages of using both Euclidean and hyperbolic spaces in video violence detection. Panel (a) shows a hierarchical structure of events in VVD, illustrating the complexity and ambiguity that can arise with violent acts. Panel (b) highlights how the Dual-Space Representation Learning (DSRL) approach balances the strengths of both spaces: Euclidean space effectively captures visual features while hyperbolic space models the complex hierarchical relationships between events, leading to improved detection of ambiguous violent events.

This figure provides a detailed overview of the Dual-Space Representation Learning (DSRL) framework. It illustrates the key components and their interactions, starting from feature preprocessing of video and audio data to the final violence score prediction. The diagram highlights the HE-GCN module (Hyperbolic Energy-constrained Graph Convolutional Network), which performs representation learning in hyperbolic space to capture hierarchical event relations. It also shows the DSI module (Dual-Space Interaction), which integrates features from both Euclidean and hyperbolic spaces. The figure details the processes within each module, including exponential mapping, hyperbolic Dirichlet energy calculation, layer-sensitive hyperbolic association degree determination, message aggregation, and cross-space attention mechanisms. The figure also visually presents the LSHAD construction rules and how the modules work together to achieve the final violence score.
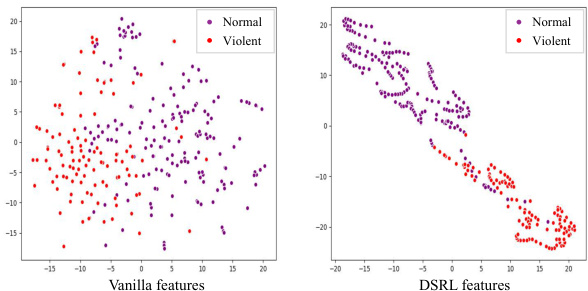
This figure shows the results of t-distributed Stochastic Neighbor Embedding (t-SNE) dimensionality reduction on the features extracted from the XD-Violence test video. The left panel displays the visualization of the original features, while the right panel shows the features obtained after applying the Dual-Space Representation Learning (DSRL) method proposed in the paper. The different colors represent different event categories (normal and violent). The visualization helps illustrate the ability of the DSRL method to better separate the features of different event categories, improving the discriminative power for violence detection.
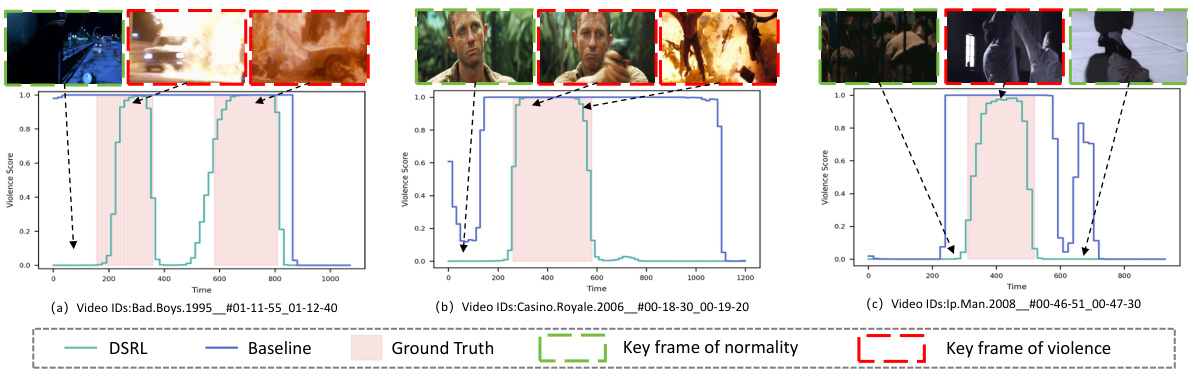
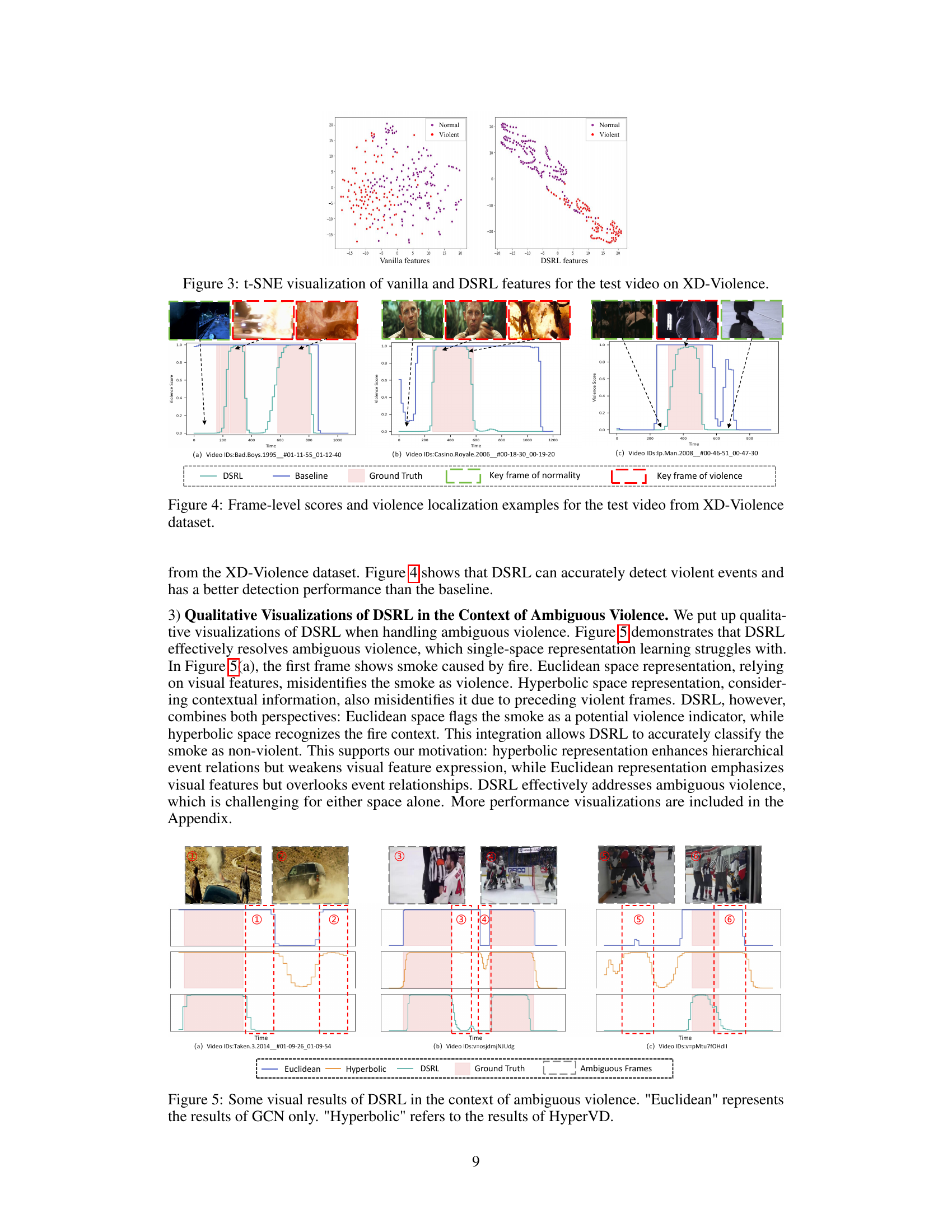
This figure visualizes the frame-level violence scores predicted by the DSRL model and a baseline model for three video clips from the XD-Violence dataset. The x-axis represents the time, while the y-axis represents the violence score. The shaded pink regions indicate the ground truth violent segments in the videos. The figure shows that DSRL more accurately identifies violent segments compared to the baseline model, as indicated by its violence scores closely aligning with the ground truth. Key frames are also highlighted to show specific examples of violent and normal events in each video clip.

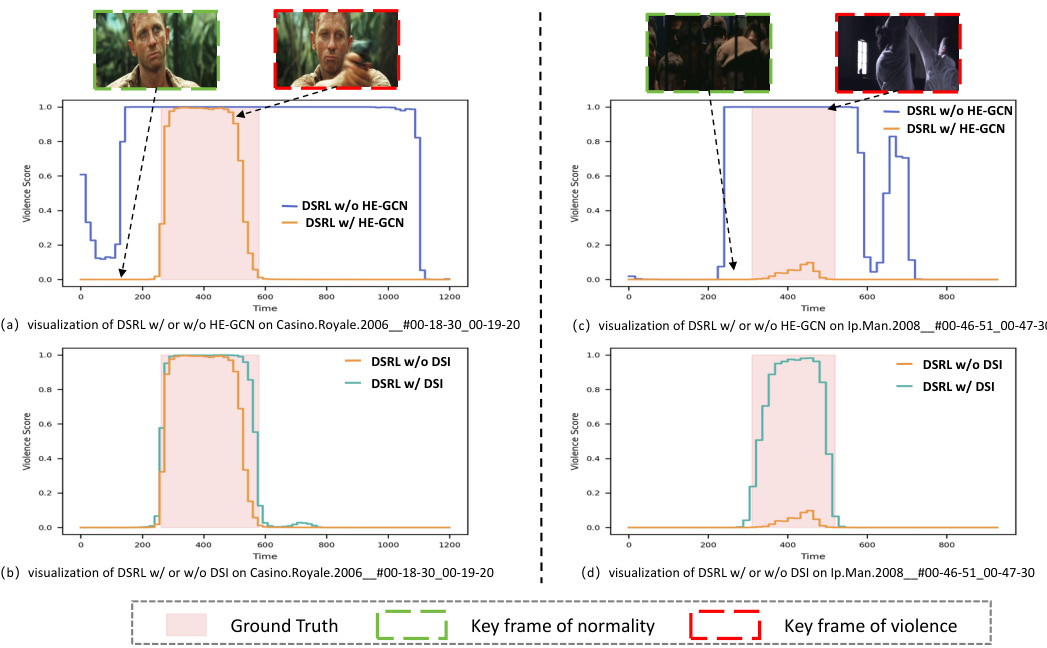
This figure presents qualitative visualizations of the Dual-Space Representation Learning (DSRL) method’s performance on ambiguous violence detection. It compares DSRL’s results with those obtained using only Euclidean space representation (GCN) and only hyperbolic space representation (HyperVD). Each subfigure shows a video clip with ambiguous violent events and the corresponding violence scores generated by each method. The results demonstrate that DSRL effectively handles ambiguous violence by combining the strengths of both Euclidean and hyperbolic geometries. Specifically, the Euclidean space representation focuses on visual features, while the hyperbolic space representation captures the hierarchical relationships between events. DSRL combines these two perspectives to achieve a superior performance in identifying violent events, even when visual cues are ambiguous.

This figure shows the t-SNE visualization of the vanilla features and the features extracted by the proposed Dual-Space Representation Learning (DSRL) method for a test video from the XD-Violence dataset. The visualization helps illustrate how DSRL improves the separability of violent and non-violent features in the feature space, enabling better classification performance. The improved separation is visually evident in the clustering of the points in the DSRL feature space compared to the vanilla features.
This figure provides a visual overview of the Dual-Space Representation Learning (DSRL) framework proposed in the paper. It illustrates the main components of the system, including feature preprocessing (handling both visual and audio inputs), the Hyperbolic Energy-constrained Graph Convolutional Network (HE-GCN) module for learning hierarchical relationships among events in hyperbolic space, the Dual-Space Interaction (DSI) module for integrating Euclidean and hyperbolic space representations, and finally, the violence score generation and loss calculation. The diagram depicts the flow of information through these different stages, showing how visual and audio features are processed, combined, and ultimately used to predict the likelihood of violent events in a video.

This figure demonstrates qualitative results of the proposed DSRL method and compares it to methods using only Euclidean or hyperbolic space representation for violence detection. It shows several video clips categorized as ambiguously violent, with frame-level violence scores calculated using the different methods. The results highlight that DSRL better identifies the true nature of ambiguously violent scenarios, outperforming the other approaches which can misclassify these scenes due to focusing only on one geometric space.

This figure shows qualitative results of the proposed Dual-Space Representation Learning (DSRL) method in handling ambiguous violent events. It compares the performance of DSRL against methods using only Euclidean space representation (GCN) and only hyperbolic space representation (HyperVD). The figure presents examples where DSRL successfully distinguishes ambiguous situations (e.g., smoke from a fire, a collision that might be interpreted as violence) while the single-space methods fail. The results demonstrate that the combined approach of DSRL effectively leverages the advantages of both Euclidean and hyperbolic spaces to improve the accuracy of violence detection in challenging scenarios.
More on tables

This table presents the ablation study results on the XD-Violence dataset. It demonstrates the impact of each component of the proposed Dual-Space Representation Learning (DSRL) method on the performance of violence detection. The table shows results for both unimodal (visual only) and multimodal (visual and audio) settings, comparing different configurations of the model: using only Euclidean geometry (GCN), adding hyperbolic geometry (HE-GCN or HGCN), the effect of concatenating Euclidean and hyperbolic features, and the impact of the Dual-Space Interaction (DSI) module using both cosine and Lorentzian metrics. The results highlight the contribution of each component and the effectiveness of the full DSRL model in improving the accuracy of violence detection.

This table compares the computing resources and training time for three different model variations: Baseline (GCN), Baseline+HE-GCN, and Baseline+HE-GCN+DSRL. It shows the number of parameters, training time per epoch, total training time, video memory usage, and the average precision (AP) achieved by each model on the XD-Violence dataset. The results highlight the computational efficiency and performance gains of the proposed DSRL method compared to simpler baselines.
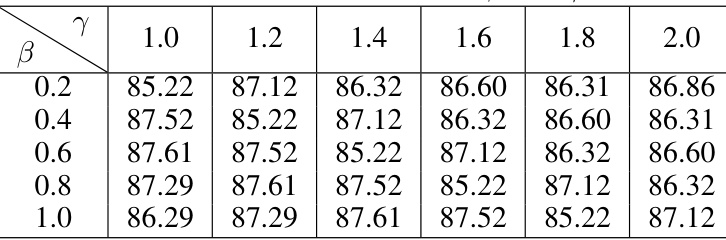
This table presents the results of ablation studies conducted on the hyperparameters β and γ within the LSHAD (Layer-Sensitive Hyperbolic Association Degree) module. Different values for β and γ were tested, and the resulting Average Precision (AP) performance on the XD-Violence dataset is shown. The goal is to determine the optimal combination of these parameters for optimal performance of the HE-GCN (Hyperbolic Energy-constrained Graph Convolutional Network) module.

This table presents the ablation study results on the hyperparameter λ in the Dual-Space Interaction (DSI) module. The average precision (AV-AP) metric is used to evaluate the performance of the model with different values of λ. The results show that the optimal value of λ is 0.8, achieving the highest AV-AP of 87.61.

This table presents the ablation study results on the hyperparameter α in the Dual-Space Interaction (DSI) module. The hyperparameter α controls the contribution of enhanced features from both Euclidean and hyperbolic spaces. The table shows the Average Precision (AV-AP) achieved on the XD-Violence dataset for different values of α, demonstrating the impact of this hyperparameter on the model’s performance. The best performance is highlighted in bold, indicating the optimal value of α for this experiment.
Full paper#