Physics-Informed Variational State-Space Gaussian Processes

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with spatio-temporal data and differential equations. It presents a novel method for integrating physical knowledge into machine learning models, leading to improved accuracy and efficiency. The linear-time complexity achieved offers significant advantages for handling large datasets and complex problems.

Visual Insights

#

This figure compares two approaches to state-space Gaussian processes (GPs): a naive approach and the physics-informed state-space GP (PHYSS-GP) proposed in the paper. The naive approach involves computing the full covariance matrix, resulting in cubic computational complexity. In contrast, PHYSS-GP uses a state-space representation, which allows for linear-time inference in the temporal dimension. This is illustrated by the different ways spatio-temporal data points are handled: the naive approach handles them in a way that leads to cubic complexity, while PHYSS-GP takes advantage of their structure for linear-time efficiency. The figure highlights the key difference in computational scaling between the two approaches.

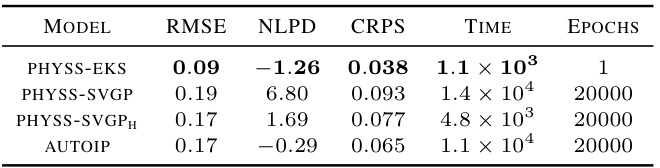
This table presents the test performance results for four different models (PHYSS-EKS, PHYSS-SVGP, PHYSS-SVGPH, and AUTOIP) on a diffusion-reaction system. The metrics used to evaluate performance include Root Mean Squared Error (RMSE), Negative Log Predictive Density (NLPD), Continuous Ranked Probability Score (CRPS), total wall clock time, and number of epochs. The results demonstrate that PHYSS-EKS achieves the best predictive performance and computational efficiency, while PHYSS-SVGPH shows similar accuracy to AUTOIP but is significantly faster.

In-depth insights

#

Variational Inference

#

Variational inference is a powerful approximate inference technique used extensively in machine learning, particularly when dealing with complex probability distributions that are intractable to compute exactly. The core idea is to approximate a complex posterior distribution with a simpler, tractable distribution. This is done by minimizing the Kullback-Leibler (KL) divergence between the true posterior and the approximate distribution. This minimization is often performed iteratively, adjusting the parameters of the approximate distribution to gradually reduce the KL divergence. The choice of the approximating family is crucial, as it determines the tractability of the calculations and the quality of the approximation. Popular choices include Gaussian distributions or mean-field approximations. The method is particularly useful for Bayesian models, where the posterior distribution over model parameters is typically difficult to compute directly. Computational efficiency is a major advantage of variational inference, enabling the application of Bayesian methods to large datasets and complex models where exact methods are infeasible. However, the quality of the approximation depends on the chosen family and the model’s complexity. A poorly chosen family could lead to a significant bias in the results, while complex models might necessitate more computationally expensive iterations. Despite this limitation, variational inference remains a key tool for many modern machine learning applications, offering a balance between accuracy and computational efficiency.

Physics-Informed GPs

#

Physics-informed Gaussian processes (GPs) represent a powerful paradigm shift in probabilistic modeling by integrating physical principles with data-driven learning. The core idea is to leverage prior knowledge about the underlying physical system, often expressed through differential equations, to constrain and regularize the GP model. This integration enhances the model’s ability to generalize to unseen data and handle complex scenarios with limited data. A key benefit lies in the ability to quantify uncertainty, inherent in both the data and the physical model. This contrasts with traditional physics-based approaches that often lack uncertainty quantification. Furthermore, variational inference techniques are crucial for making the computations tractable, especially for large datasets and complex models. The fusion of mechanistic understanding with the flexibility and uncertainty quantification of GPs offers a compelling approach across diverse scientific and engineering domains, addressing challenges of data scarcity and the need for reliable uncertainty estimates.

Spatiotemporal Modeling

#

Spatiotemporal modeling, the simultaneous analysis of spatial and temporal patterns, presents unique challenges and opportunities in various fields. The integration of these dimensions requires sophisticated methods that can capture complex interactions and dependencies. Statistical methods, such as spatial and spatiotemporal autoregressive models, or machine learning techniques, like recurrent neural networks or spatiotemporal Gaussian processes, are commonly used. The choice of method often depends on the specific data characteristics, including the dimensionality, the presence of non-linear relationships, and the computational resources available. Effective spatiotemporal modeling demands careful consideration of data preprocessing, model selection, and validation to ensure robust and meaningful insights. Handling missing data and quantifying uncertainty are critical aspects. Additionally, interpretability and visualization are important for understanding the underlying dynamics.

Computational Efficiency

#

The research paper emphasizes computational efficiency as a critical aspect of the proposed physics-informed state-space Gaussian process (PHYSS-GP) model. Traditional methods for incorporating physical knowledge into Gaussian processes often suffer from cubic computational complexity, particularly concerning the spatial dimension. In contrast, PHYSS-GP leverages a variational inference framework and a state-space representation to achieve linear-in-time computational cost for temporal data. Furthermore, the authors explore several approximations such as spatial inducing points and structured variational posteriors to reduce the cubic spatial complexity to linear, significantly enhancing scalability. This focus on efficiency is particularly relevant when dealing with large-scale spatio-temporal datasets, enabling the application of physics-informed machine learning to complex real-world problems that were previously intractable. The reported empirical results demonstrate that PHYSS-GP outperforms existing methods, showcasing its advantage in both predictive accuracy and computational speed.

Scalability

#

The scalability of physics-informed Gaussian processes (GPs) is a crucial aspect determining their applicability to large-scale problems. Traditional GP inference methods suffer from cubic computational complexity, limiting their use to relatively small datasets. This paper tackles this limitation head-on by introducing several key innovations. First, a variational inference framework is developed enabling linear-in-time computational costs for temporal dimensions. Second, spatial scalability is addressed through three distinct approximations: structured variational inference, spatial inducing points, and spatial mini-batching. Each of these cleverly leverages the structure of the GP model and underlying physics to reduce computational cost without significant loss of predictive accuracy. The use of inducing points, in particular, is a standard technique in GP literature but its adaptation to the spatio-temporal state-space is a notable contribution, and the combination of these techniques is shown to be highly effective in scaling the approach to significantly larger datasets than previously feasible. Experimental validation using several datasets including real-world applications demonstrates these gains in scalability, ultimately opening up the possibility of applying physics-informed GPs to problems previously intractable due to their high dimensionality and data volume.

More visual insights

#

More on figures

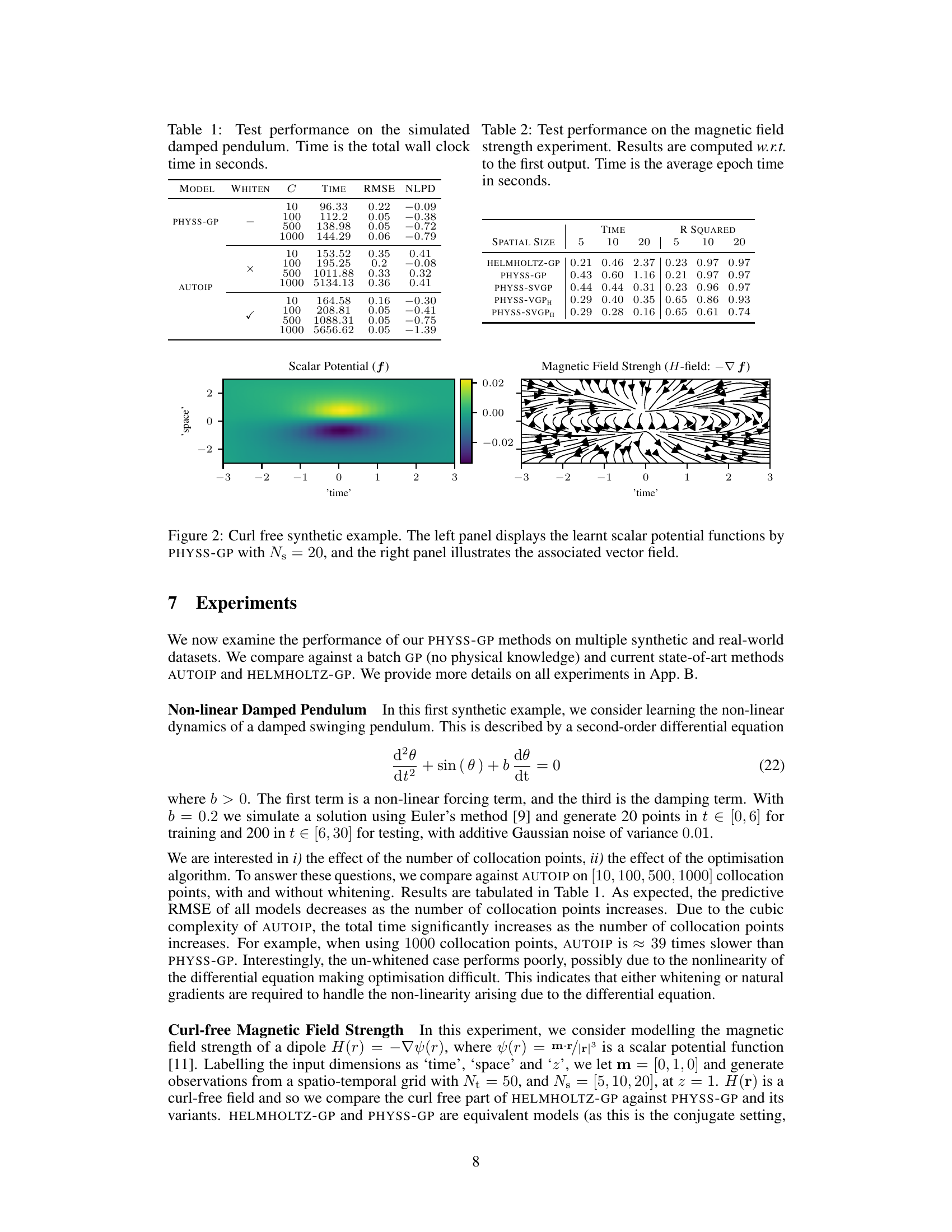
This figure shows the results of a curl-free synthetic experiment. The left panel is a heatmap visualization of the scalar potential function learned by the PHYSS-GP model (Physics-Informed State-Space Gaussian Processes), with 20 spatial points (N₃ = 20). The right panel displays the corresponding vector field, which is derived from the scalar potential. This demonstrates the model’s ability to capture both the scalar potential and its associated vector field in a curl-free setting.

This figure compares the predictive performance of three different methods (PHYSS-EKS, AUTOIP, and PHYSS-SVGPH) on a diffusion-reaction system. The top row shows the predictive mean for each method, while the bottom row displays the 95% confidence intervals. A vertical white line indicates the boundary between the training and testing data. The figure highlights that PHYSS-EKS accurately captures the sharp boundaries of the solution, attributed to its use of an integrated Wiener kernel (IWP). PHYSS-SVGPH achieves comparable results to AUTOIP but with significantly reduced computational cost.

This figure shows the results of a curl-free synthetic experiment. The left panel displays the scalar potential functions learned by the PHYSS-GP model, where N₃ represents the number of spatial points, set to 20. The right panel visually represents the associated vector field, providing a visual interpretation of the learned scalar potential. The purpose is to demonstrate the model’s effectiveness in handling curl-free constraints.

This figure compares the predictive distributions of a standard Gaussian Process (GP) and the proposed Physics-Informed State-Space Gaussian Process (PHYSS-GP) on a monotonic function. The GP model, unable to incorporate prior knowledge about monotonicity, simply fits the data points without capturing the underlying monotonic trend. In contrast, PHYSS-GP, leveraging this information, accurately learns and predicts the monotonic behavior of the function.

This figure compares the predictive performance of PHYSS-GP and AUTOIP on the damped pendulum problem for different numbers of collocation points (C=10 and C=1000). Each panel shows the true data (black dots), the predictive mean (line), and 95% confidence intervals (shaded area) for each model. The plot demonstrates the improvement in accuracy and uncertainty quantification offered by PHYSS-GP compared to AUTOIP, especially with a higher number of collocation points.

Full paper

#