TL;DR#
Deep neural networks (DNNs) are vulnerable to adversarial attacks, which often manipulate the phase information of an image’s frequency spectrum more than the amplitude. Existing adversarial training methods struggle to address this vulnerability, leading to models that are easily fooled by cleverly disguised inputs. This paper introduces a novel Dual Adversarial Training (DAT) method to improve the robustness of DNNs.
DAT leverages a new Adversarial Amplitude Generator (AAG) to create a more effective adversarial training strategy. By mixing the amplitude of training samples with those of distractor images, the model learns to focus on phase information, which is less susceptible to manipulation. This technique, combined with an efficient adversarial example generation procedure, leads to a significant improvement in model robustness against various attacks. Experiments on multiple datasets confirm the effectiveness of the proposed approach, showing that DAT consistently surpasses state-of-the-art methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in adversarial robustness because it identifies a critical vulnerability in existing adversarial training methods and proposes a novel approach to improve the model’s robustness against various attacks. The findings are significant for advancing the understanding of adversarial attacks’ impact on frequency domain and developing more robust models for real-world applications. This work also opens new avenues of research in adversarial training and frequency spectrum analysis.
Visual Insights#

🔼 The figure shows a comparison between a benign image and its adversarial example (AE). It highlights that adversarial attacks primarily affect the phase component of the image’s frequency spectrum, while leaving the amplitude largely unchanged. The red rectangle emphasizes a region where phase patterns are particularly affected by the adversarial perturbation. This observation motivates the proposed method, which focuses on improving robustness by leveraging the less-perturbed amplitude information.
read the caption
Figure 1: The adversarial perturbation severely damages phase patterns (especially in red rectangular) and the frequency spectrum, while amplitude patterns are rarely impacted. The AE is generated by PGD-20 l∞-bounded with radius 8/255.

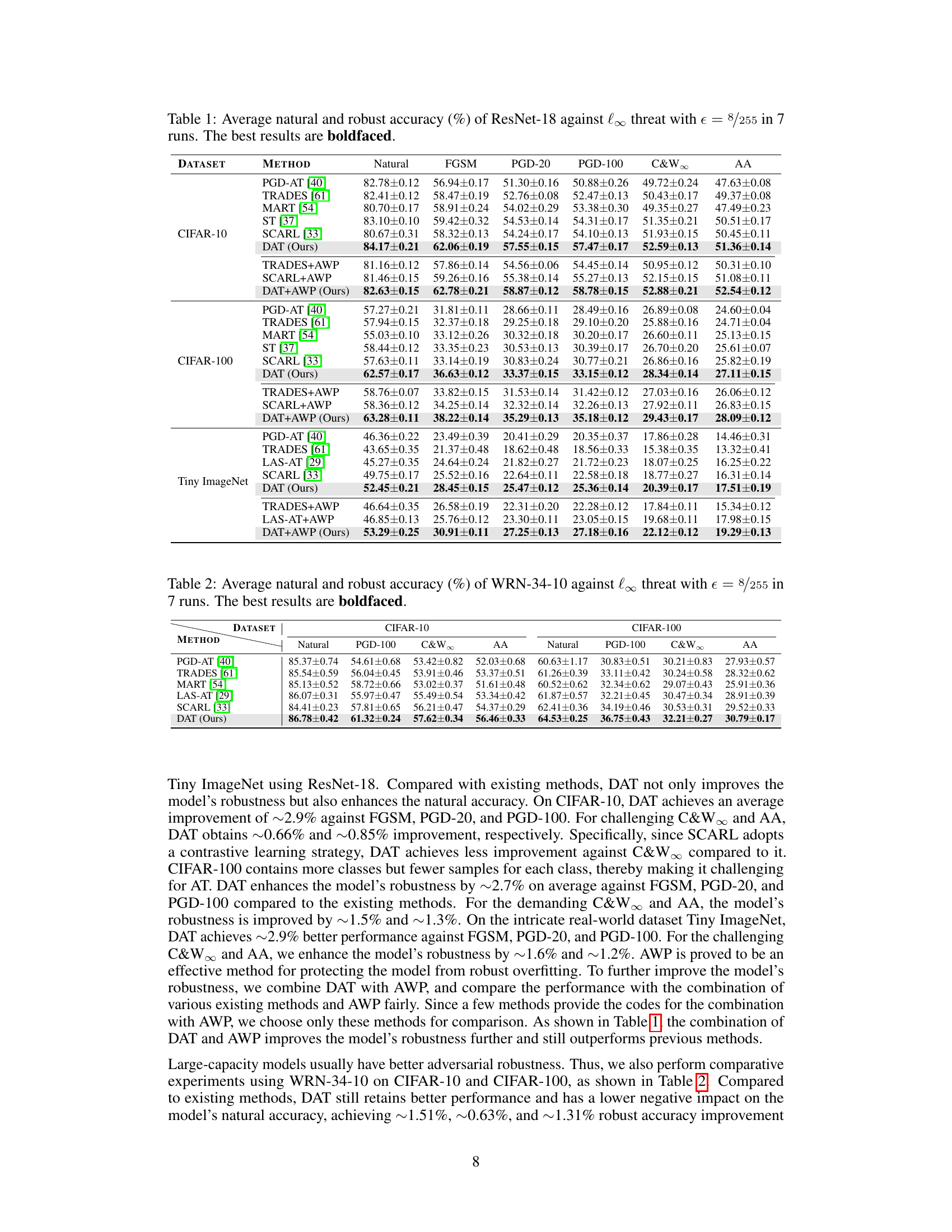
🔼 This table presents the average natural and robust accuracy of ResNet-18, a convolutional neural network model, against different adversarial attacks. The attacks use an L-infinity norm with a perturbation budget (epsilon) of 8/255. The table includes results for multiple attacks, and the best results are highlighted in bold. This data is used to compare the performance of DAT (Dual Adversarial Training), the proposed method, against other state-of-the-art adversarial training techniques.
read the caption
Table 1: Average natural and robust accuracy (%) of ResNet-18 against l∞ threat with e = 8/255 in 7 runs. The best results are boldfaced.
In-depth insights#
Freq Domain AT#
Frequency domain adversarial training (Freq Domain AT) offers a unique perspective on enhancing model robustness. Instead of focusing solely on the spatial domain, Freq Domain AT leverages the frequency representation of images, analyzing amplitude and phase components separately. This allows for a more nuanced understanding of how adversarial perturbations affect the model’s decision-making process. By manipulating the amplitude or phase components in the frequency domain during training, researchers can potentially improve model’s resilience against adversarial attacks while preserving its accuracy on clean images. A key challenge lies in determining the optimal way to modify the frequency components—too much alteration can disrupt essential semantic information encoded in the phase, while insufficient modification may not provide sufficient robustness improvement. Therefore, carefully designed generative models or other techniques become crucial to find the right balance, thereby improving the effectiveness of Freq Domain AT.
AAG Generator#
The Adversarial Amplitude Generator (AAG) is a crucial component of the proposed Dual Adversarial Training (DAT) framework. Its primary function is to generate adversarial amplitudes in the frequency domain for training images. By strategically mixing these generated amplitudes with the original image amplitudes, the AAG aims to force the model to focus more on the phase information which is less susceptible to adversarial attacks. This is a key innovation because adversarial attacks often disproportionately affect the phase component. The AAG’s design is optimized to maintain the integrity of the phase patterns while maximizing the model’s loss on the manipulated training data. This optimization is crucial for the success of DAT in enhancing adversarial robustness. The effectiveness of the AAG is experimentally validated showing its contribution to the improved robustness achieved by DAT over existing adversarial training methods.
DAT Framework#
The DAT framework introduces a novel Dual Adversarial Training approach to enhance the robustness of deep neural networks against adversarial attacks. It leverages a generative adversarial network (GAN) to create adversarial amplitude perturbations in the frequency domain, forcing the model to focus on phase patterns which are less susceptible to manipulation. This contrasts with traditional adversarial training methods that primarily focus on pixel-level perturbations. The framework involves three stages: adversarial amplitude generation, adversarial example generation, and joint optimization. The optimized Adversarial Amplitude Generator (AAG) is crucial, ensuring that amplitude mixing enhances robustness without significantly disrupting phase information. By combining this with an efficient adversarial example generation process, DAT demonstrates improved robustness across multiple datasets and against various adversarial attacks, highlighting the significance of frequency domain considerations for adversarial defense.
Robustness Gains#
The concept of “Robustness Gains” in the context of a research paper on improving the adversarial robustness of deep neural networks (DNNs) refers to the quantifiable improvements in a model’s resistance to adversarial attacks after applying a novel training method or technique. These gains are typically measured through higher accuracy on adversarially perturbed test data compared to a baseline model trained with standard methods. The magnitude of the gains is a key indicator of the effectiveness of the proposed approach, often reported as a percentage increase in accuracy or a decrease in error rate under various attack scenarios. A comprehensive analysis of robustness gains would consider factors such as the types of adversarial attacks used (e.g., FGSM, PGD, C&W), the strength of the attacks (perturbation budget), and the specific dataset used for evaluation. Furthermore, a well-rounded discussion would compare the robustness gains against the state-of-the-art methods, demonstrating a clear advantage of the proposed technique. Finally, the analysis should explore any trade-offs between robustness gains and other metrics, such as natural accuracy or computational cost, to provide a balanced assessment of the overall improvements.
Future of DAT#
The future of DAT (Dual Adversarial Training) hinges on addressing its current limitations and exploring new avenues for improvement. Improving efficiency is crucial; DAT’s computational cost can be prohibitive, especially with complex models and large datasets. Future research should focus on optimizing the Adversarial Amplitude Generator (AAG) for faster convergence and reduced computational overhead. Enhanced robustness against diverse attacks is another key area. While DAT shows promise, further evaluation and improvement are needed to ensure effectiveness across different attack strategies and perturbation levels, especially against stronger, more adaptive attacks. Expanding DAT’s applicability to other domains and modalities beyond image classification is also important. Its principles could be adapted to tackle adversarial robustness issues in areas like natural language processing and time series analysis. Finally, theoretical understanding needs further development. More rigorous analysis is needed to fully understand the interplay between phase and amplitude information, to refine DAT’s optimization and guide future enhancements.
More visual insights#
More on figures
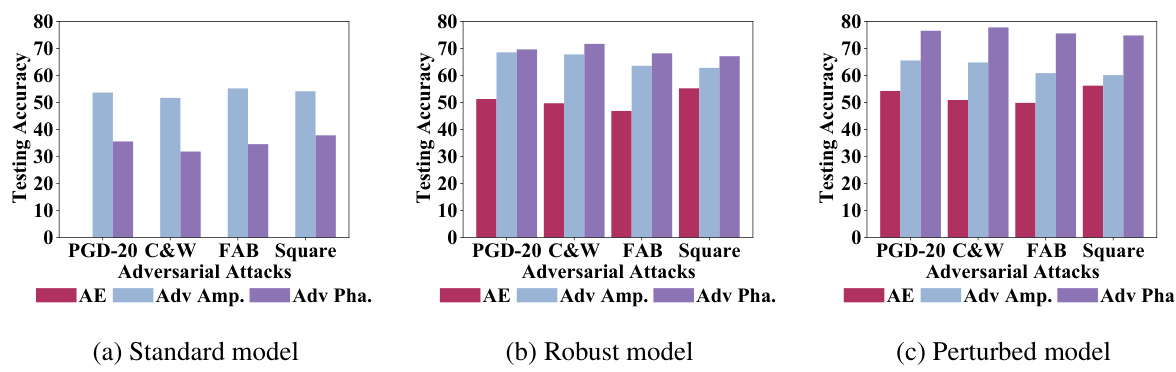
🔼 This figure compares the performance of three different ResNet-18 models (standard, robust, and amplitude-perturbed) on CIFAR-10 dataset against various adversarial attacks (PGD-20, C&W, FAB, Square). The robust model is trained with adversarial training, and the perturbed model is trained with amplitude-perturbed samples. The chart shows test accuracy for each model under different attacks and whether adversarial perturbations were applied to the amplitude or phase components of the frequency spectrum. The results demonstrate the impact of adversarial perturbations on phase and amplitude patterns and the effectiveness of adversarial training and amplitude perturbation in improving model robustness.
read the caption
Figure 2: Test accuracy (%) on CIFAR-10 of (a) standard, (b) robust, and (c) amplitude-perturbed ResNet-18. 'Adv Amp./Pha.' refers to x'amp/xpha. AEs are generated by PGD-20, C&W∞, FAB, and Square, with l∞-bounded perturbation budget e = 8/255 and inner step a = 2/255. The robust and perturbed models are trained by PGD-AT-10 following [40].

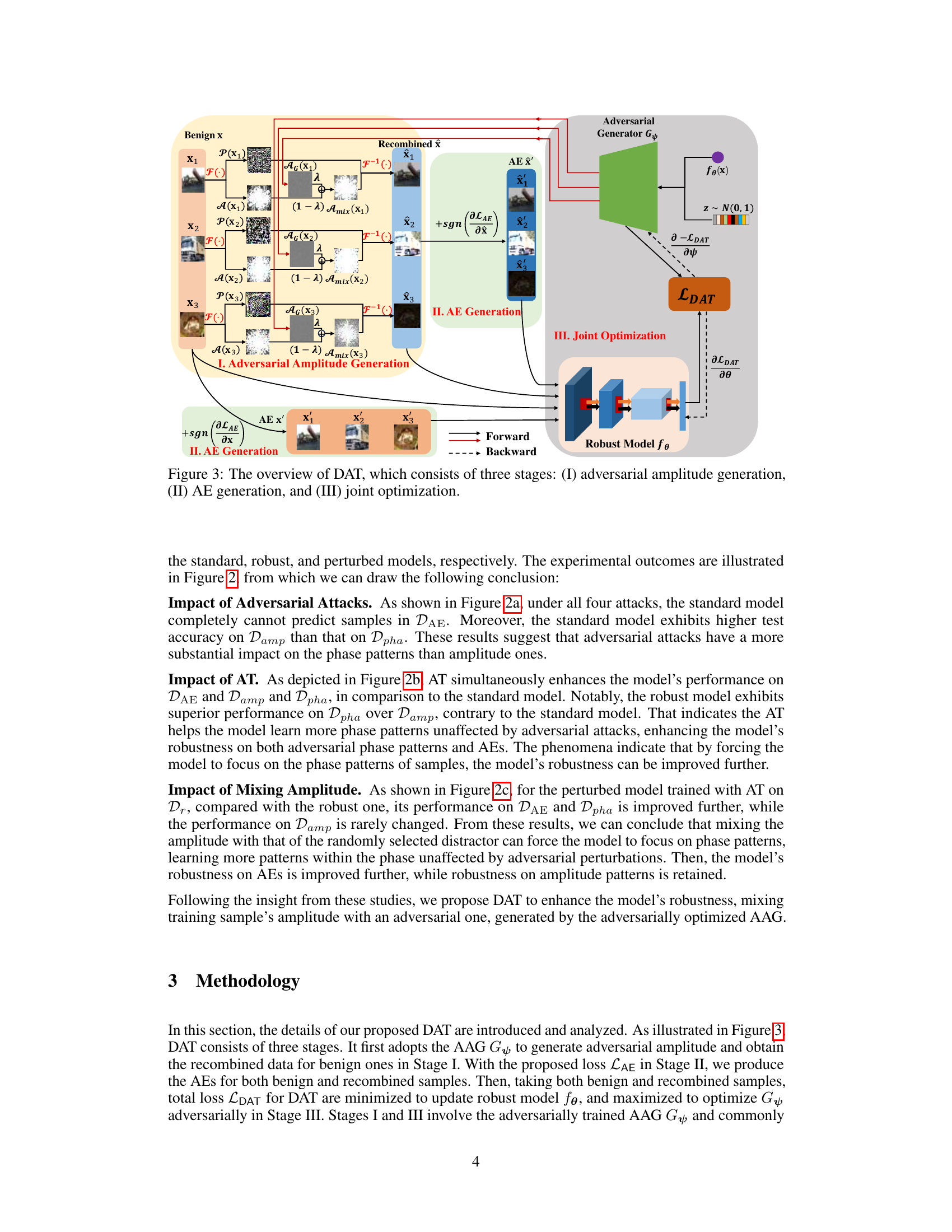
🔼 The figure illustrates the Dual Adversarial Training (DAT) framework, highlighting its three main stages. Stage I focuses on generating adversarial amplitudes using an Adversarial Amplitude Generator (AAG). Stage II involves generating adversarial examples (AEs) using an efficient AE generation module. Finally, Stage III performs joint optimization, updating both the robust model and the AAG adversarially using the combined loss function LDAT. The figure visually depicts the data flow and the interactions between these three stages, showing the forward and backward passes during the training process.
read the caption
Figure 3: The overview of DAT, which consists of three stages: (I) adversarial amplitude generation, (II) AE generation, and (III) joint optimization.
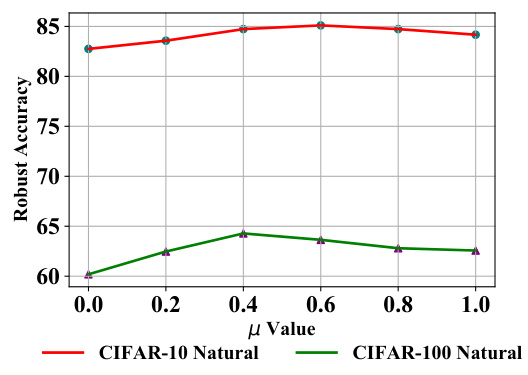
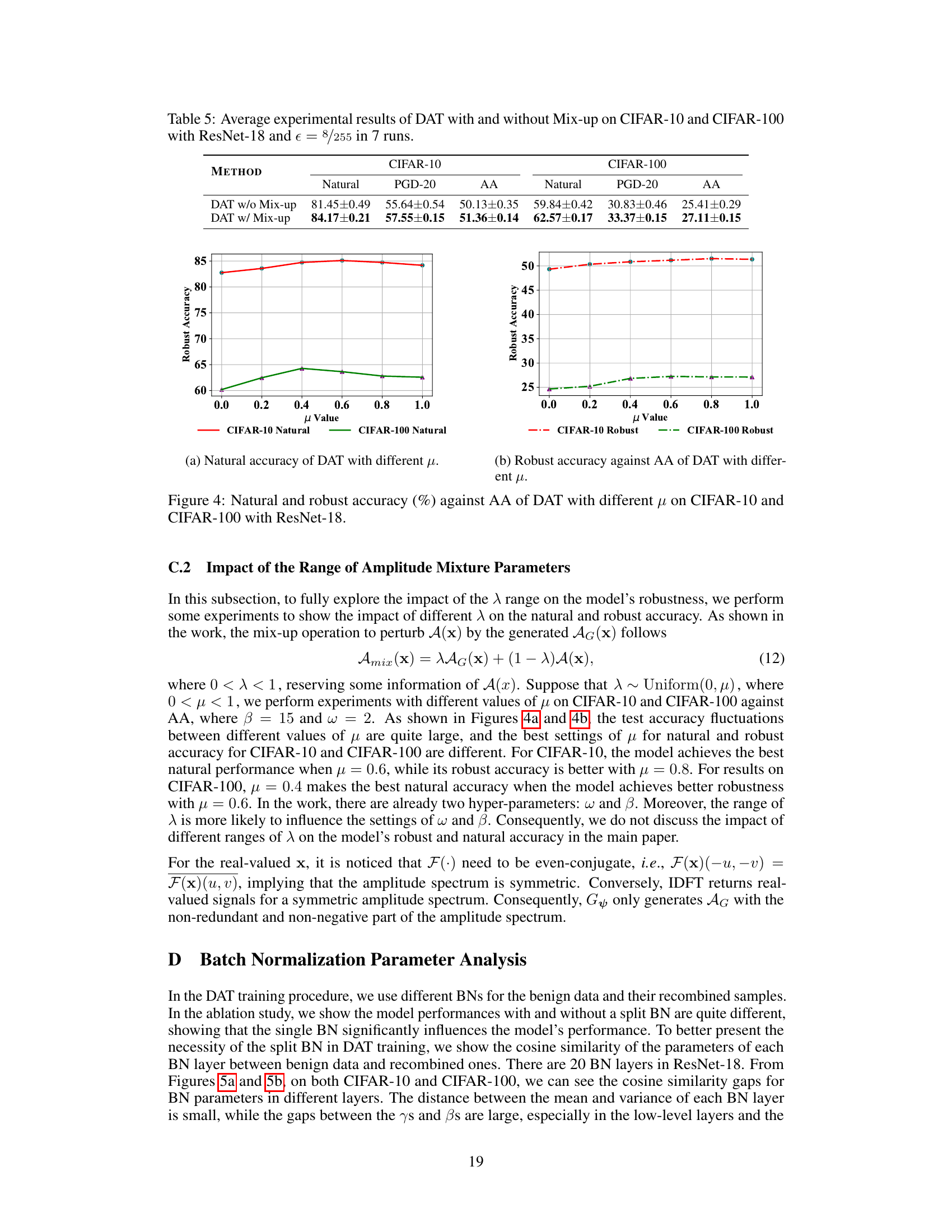
🔼 This figure shows the impact of different values of the mixing parameter μ on the natural and robust accuracy against the AutoAttack (AA) on CIFAR-10 and CIFAR-100 datasets using ResNet-18. The x-axis represents the μ value (from 0 to 1), and the y-axis represents the accuracy. Two lines for each dataset are presented, where one represents the natural accuracy and the other represents the robust accuracy against AA.
read the caption
Figure 4: Natural and robust accuracy (%) against AA of DAT with different μ on CIFAR-10 and CIFAR-100 with ResNet-18.

🔼 This figure shows the impact of the range of amplitude mixture parameters (μ) on the model’s robustness against the AutoAttack (AA) on CIFAR-10 and CIFAR-100 datasets. The ResNet-18 model was used. The x-axis represents the μ value, which controls the mixing of the original amplitude spectrum with the generated adversarial amplitude. The y-axis shows the robust accuracy. Separate lines show the results for CIFAR-10 and CIFAR-100. The plot indicates that there’s an optimal range for μ that balances robustness and natural accuracy, with performance varying across datasets.
read the caption
Figure 4: Natural and robust accuracy (%) against AA of DAT with different μ on CIFAR-10 and CIFAR-100 with ResNet-18.
🔼 This figure shows the impact of adversarial attacks on the frequency spectrum of an image. The adversarial perturbation significantly affects the phase component of the frequency spectrum (especially the red rectangular area), which is responsible for semantic information. The amplitude component, however, remains largely unaffected. This observation is important because it suggests that adversarial robustness can be enhanced by focusing on the phase patterns that are less impacted by adversarial attacks.
read the caption
Figure 1: The adversarial perturbation severely damages phase patterns (especially in red rectangular) and the frequency spectrum, while amplitude patterns are rarely impacted. The AE is generated by PGD-20 l∞-bounded with radius 8/255.
🔼 This figure shows the impact of adversarial perturbations on the frequency spectrum of an image. Adversarial examples (AEs) are created by adding small, imperceptible perturbations to a benign image. The figure compares the frequency spectrum of the benign image to that of its corresponding AE. The key observation is that adversarial attacks disproportionately impact the phase component of the frequency spectrum, while leaving the amplitude component relatively unchanged. This difference is highlighted by the red rectangular, showing a severe change in the phase patterns of the AE compared to the original image. This is important because the phase of the frequency spectrum is thought to contain more semantically meaningful information than the amplitude.
read the caption
Figure 1: The adversarial perturbation severely damages phase patterns (especially in red rectangular) and the frequency spectrum, while amplitude patterns are rarely impacted. The AE is generated by PGD-20 l∞-bounded with radius 8/255.

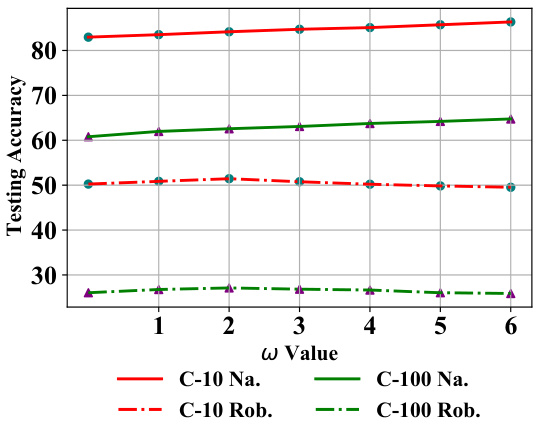
🔼 This figure shows the impact of hyperparameters β and w on the model’s performance. The x-axis represents the β values, while the y-axis shows the testing accuracy. The lines represent the natural accuracy and robust accuracy against adversarial attacks (AA) on CIFAR-10 and CIFAR-100 datasets. It demonstrates the effect of tuning these parameters for balancing natural accuracy and robustness.
read the caption
Figure 6: The impact of w and β on the model's natural (Na.) and robust accuracy (Rob.) against AA on CIFAR-10 (C-10) and CIFAR-100 (C-100) with ResNet-18.
🔼 The figure shows the impact of the range of amplitude mixture parameters (μ) on the model’s robustness against adversarial attacks. The plots display natural accuracy (how well the model performs on regular images) and robust accuracy (how well the model performs on images with adversarial attacks added) on CIFAR-10 and CIFAR-100 datasets using ResNet-18 model. It demonstrates how different values of μ affect both natural and robust accuracy. The optimal value of μ balances the improvement in robustness against the potential decrease in natural accuracy.
read the caption
Figure 4: Natural and robust accuracy (%) against AA of DAT with different μ on CIFAR-10 and CIFAR-100 with ResNet-18.
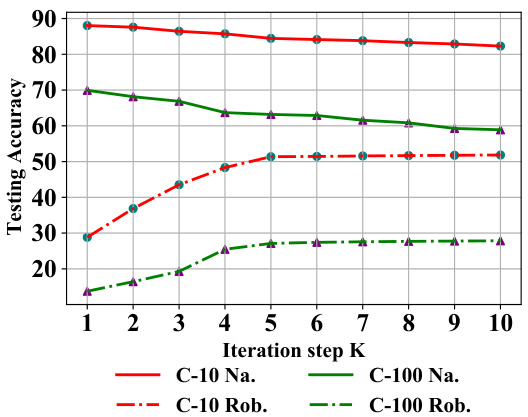
🔼 This figure shows how the number of iterations in the adversarial example generation process affects the model’s performance. The x-axis represents the number of iterations (K), and the y-axis shows the testing accuracy. There are four lines, representing the natural accuracy and robustness against the AutoAttack (AA) for both CIFAR-10 and CIFAR-100 datasets. The figure demonstrates that increasing K improves robustness against AA, especially for CIFAR-100, but at a cost of potentially reducing natural accuracy, suggesting an optimal K exists that balances robustness and natural accuracy.
read the caption
Figure 7: The impact of different iteration step K on the model's performance on natural data and against AA on CIFAR-10 and CIFAR-100 with ResNet-18.
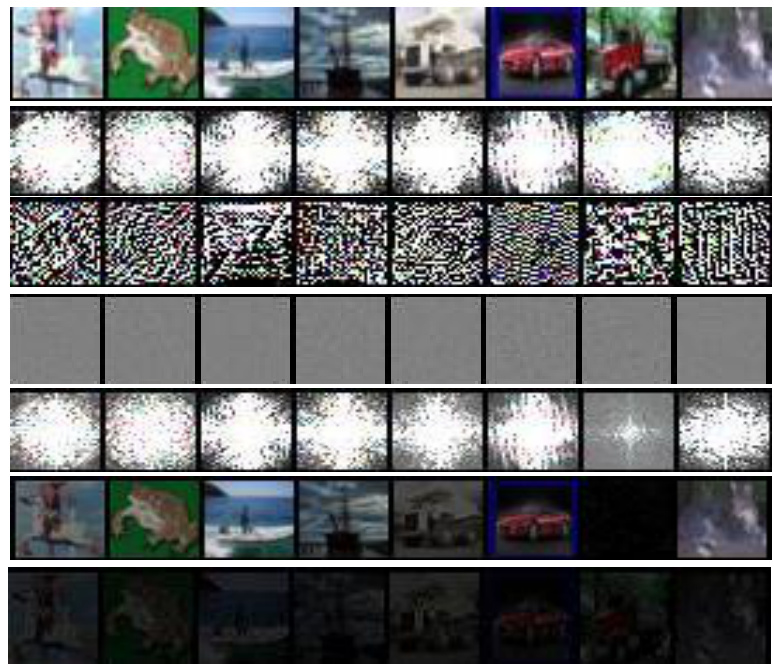
🔼 This figure visualizes the impact of the amplitude mix-up operation on the generated recombined samples. It shows original benign samples, their amplitude and phase spectrums, the generated adversarial amplitude spectrum, the mixed amplitude spectrum (combining original and generated), the recombined image using the mixed amplitude and the original phase, and finally, a recombined image using only the generated adversarial amplitude. This allows for a visual comparison of how the different approaches to amplitude modification affect the resulting recombined images.
read the caption
Figure 8: Visualization of recombined samples w/wo mix-up.

🔼 This figure visualizes the impact of different inputs to the Adversarial Amplitude Generator (AAG) on the generated amplitude spectrum, mixed amplitude spectrum, and the final recombined image. Three variations are shown: using only random noise, using random noise plus the image label, and using random noise plus the model’s logits. The results demonstrate how different inputs affect the AAG’s output and consequently influence the characteristics of the resulting recombined images.
read the caption
Figure 9: Visualization of recombined samples based on the amplitude spectrum generated by different inputs of AAG.
More on tables

🔼 This table presents the average natural accuracy and robust accuracy achieved by different adversarial training methods using ResNet-18 on CIFAR-10 and CIFAR-100 datasets. Robust accuracy is evaluated against four different adversarial attacks: FGSM, PGD-20, PGD-100, C&W∞, and AutoAttack (AA). The best performing method for each metric is highlighted in bold.
read the caption
Table 1: Average natural and robust accuracy (%) of ResNet-18 against l∞ threat with = 8/255 in 7 runs. The best results are boldfaced.
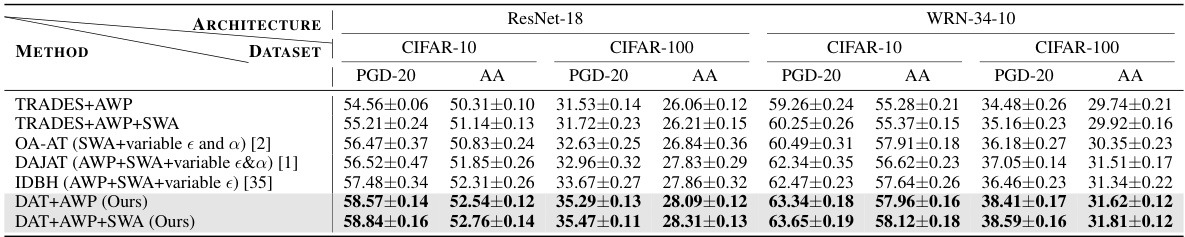
🔼 This table compares the performance of DAT against other state-of-the-art methods that utilize complex training strategies such as AWP and SWA. It shows the average robust accuracy of different models (ResNet-18 and WRN-34-10) trained on CIFAR-10 and CIFAR-100 datasets against PGD-20 and AA attacks. The best results for each metric are highlighted in bold.
read the caption
Table 3: The average experimental results for methods with complex strategies against l∞ threat model with e = 8/255 in 7 runs. The best results are boldfaced.
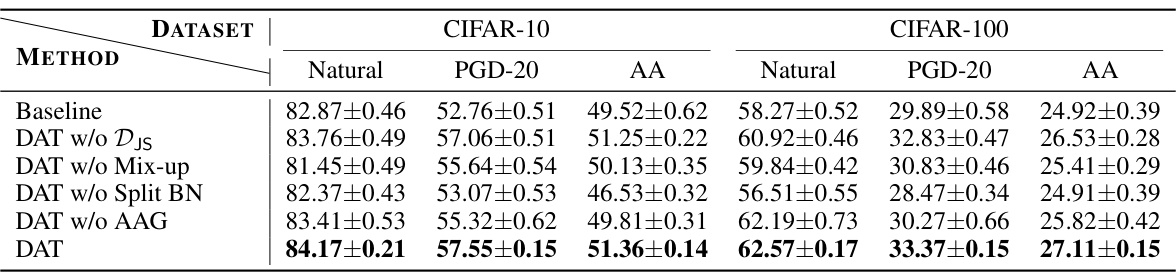
🔼 This table presents the results of ablation studies conducted to analyze the impact of different components of the proposed DAT method on the model’s performance. The baseline represents the model’s performance without any of the DAT components. Subsequent rows show the impact of removing specific components (DjS loss, mix-up operation, split batch normalization, and the Adversarial Amplitude Generator) on the model’s natural and robust accuracy (against PGD-20 and AA attacks) on CIFAR-10 and CIFAR-100 datasets.
read the caption
Table 4: Results of ablation studies with ResNet-18 against l∞ with € = 8/255 average in 7 runs.

🔼 This table presents the average natural and robust accuracy of ResNet-18 against different adversarial attacks (FGSM, PGD-20, PGD-100, C&W, and AutoAttack) with a perturbation budget of 8/255. The results are averaged over 7 runs, and the best performance for each attack is highlighted in bold. The table shows the model’s performance on clean images (natural accuracy) and on adversarially perturbed images (robust accuracy), demonstrating the impact of adversarial training.
read the caption
Table 1: Average natural and robust accuracy (%) of ResNet-18 against l∞ threat with e = 8/255 in 7 runs. The best results are boldfaced.

🔼 This table presents the average natural and robust accuracy of ResNet-18 against different l∞-bounded adversarial attacks. The results are obtained across seven independent runs, with the best performance for each metric highlighted in bold. The attacks include Fast Gradient Sign Method (FGSM), Projected Gradient Descent (PGD) with 20 and 100 iterations, Carlini and Wagner (C&W) attack, and AutoAttack (AA). The table helps compare the performance of the model in terms of natural accuracy (accuracy on clean images) and robustness to various attacks (accuracy on adversarially perturbed images).
read the caption
Table 1: Average natural and robust accuracy (%) of ResNet-18 against l∞ threat with = 8/255 in 7 runs. The best results are boldfaced.

🔼 The table shows the average natural and robust accuracy (%) of the DAT model with and without the amplitude mix-up operation on CIFAR-10 and CIFAR-100 datasets, using ResNet-18 as the model architecture and an (\ell_\infty) threat with (\epsilon = 8/255). The results are averaged over 7 runs. It compares the performance of DAT with and without the amplitude mixing component, demonstrating the impact of this component on the model’s performance against different attacks.
read the caption
Table 5: Average experimental results of DAT with and without Mix-up on CIFAR-10 and CIFAR-100 with ResNet-18 and \(\epsilon = 8/255\) in 7 runs.

🔼 This table compares the performance of different data augmentation methods on CIFAR-10 using the WRN-28-10 architecture against an l∞-bounded threat with a perturbation budget of 8/255. The methods include various combinations of data augmentation techniques, such as those from Rebuffi et al., Gowal et al., Wang et al., and IKL-AT. The table shows the natural accuracy and the robust accuracy against AutoAttack (AA) for each method. The best results for each metric are highlighted in bold.
read the caption
Table 6: The average experimental results for different augmentations against l∞ threat model with € = 8/255 on CIFAR-10. #Aug. refers to the number of augmentation. The best results are boldfaced.

🔼 This table shows the average natural and robust accuracy of different methods on CIFAR-100 using WideResNet-28-10 architecture against an l∞-bounded adversarial attack with a perturbation budget of 8/255. The results are averaged over 7 runs. The table compares the performance of various methods, including those using different data augmentation strategies. The number of augmentations used by each method is indicated in the #Aug column. The best results for each metric are highlighted in bold.
read the caption
Table 7: The average experimental results for different augmentations against l∞ threat model with e = 8/255 on CIFAR-100. #Aug. refers to the number of augmentation. The best results are boldfaced.

🔼 This table presents the average experimental results of different data augmentation methods combined with the proposed AE generation strategy against the l∞ threat model on CIFAR-10 and CIFAR-100 datasets. The results are obtained by averaging 7 runs, with the best results being boldfaced. The augmentations include CutOut, CutMix, and AutoAugment. The table shows the natural accuracy and robust accuracy against PGD-20 and AA attacks for each augmentation strategy, allowing comparison with the proposed DAT (Dual Adversarial Training) method.
read the caption
Table 8: The average experimental results for different augmentations against l∞ threat model with = 8/255 in 7 runs. The best results are boldfaced.

🔼 This table presents the time consumption in seconds for each training epoch across different adversarial training (AT) methods. The methods compared are PGD-AT, TRADES, ST, SCARL, and the proposed DAT method. The time is measured separately for the CIFAR-10 and CIFAR-100 datasets.
read the caption
Table 9: Time consumption (s) of each training epoch for different AT methods.

🔼 This table presents the average experimental results of combining the proposed Adversarial Amplitude Generator (AAG) with existing adversarial training (AT) methods, specifically PGD-AT and TRADES, on the CIFAR-10 and CIFAR-100 datasets. The results are evaluated using ResNet-18 and a perturbation budget of epsilon = 8/255. The table compares the natural accuracy and robust accuracy (against PGD-20 and AutoAttack) for each method, demonstrating the performance improvement achieved by incorporating the AAG into the AT process.
read the caption
Table 10: Average experimental results of AAG with existing AT methods on CIFAR-10/100 with ResNet-18 and = 8/255 in 7 runs.

🔼 This table presents the average experimental results obtained using different inputs for the generator Gψ in the proposed DAT method. The experiments were conducted using ResNet-18 with an 𝑙∞-bounded threat parameter ∈ = 8/255, and the results are averaged over 7 runs. Three input variations were tested: using only the noise vector z; using z plus a one-hot label; and using z plus the logits. The table shows the natural accuracy and robustness against PGD-20 and AA attacks for CIFAR-10 and CIFAR-100 datasets.
read the caption
Table 11: Average experimental results of different inputs of Gy with ResNet-18 and ∈ = 8/255 in 7 runs.

🔼 This table compares the performance of the DAT model using single and dual AE generation strategies. It shows the natural accuracy, and robust accuracy against PGD-20 and AA attacks on CIFAR-10 and CIFAR-100 datasets using the ResNet-18 model. The results are averaged over 7 runs, with the perturbation budget set to ϵ = 8/255. The comparison highlights the impact of using dual AE generation versus single AE generation on the model’s performance.
read the caption
Table 12: Average experimental results with single and dual AE on CIFAR-10 and CIFAR-100 with ResNet-18 and = 8/255 in 7 runs.
Full paper#