TL;DR#
In-context learning (ICL) is a crucial capability of large language models, allowing them to perform new tasks based on a few examples without retraining. While previous research focused on linear self-attention models, their limitations in handling scenarios with shared signals among tasks remained unaddressed. This paper explores these shortcomings in ICL of linear regression tasks, showing that the existing models incur irreducible errors.
This research introduces the Linear Transformer Block (LTB), demonstrating that it significantly improves ICL performance by implementing one-step gradient descent with learnable initialization. The study highlights the crucial role of the MLP component in reducing approximation errors and achieving near-optimal ICL, even when tasks share a common signal. The findings provide valuable insights into how Transformers perform ICL and suggest new avenues for optimization and model improvement.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in in-context learning and transformer model interpretability. It provides novel theoretical insights into the workings of transformer blocks, particularly highlighting the role of MLP layers. By connecting the model to gradient descent, the authors open new avenues for efficient optimization and improved ICL performance. These findings are highly relevant to ongoing efforts to understand and improve the capabilities of large language models.
Visual Insights#
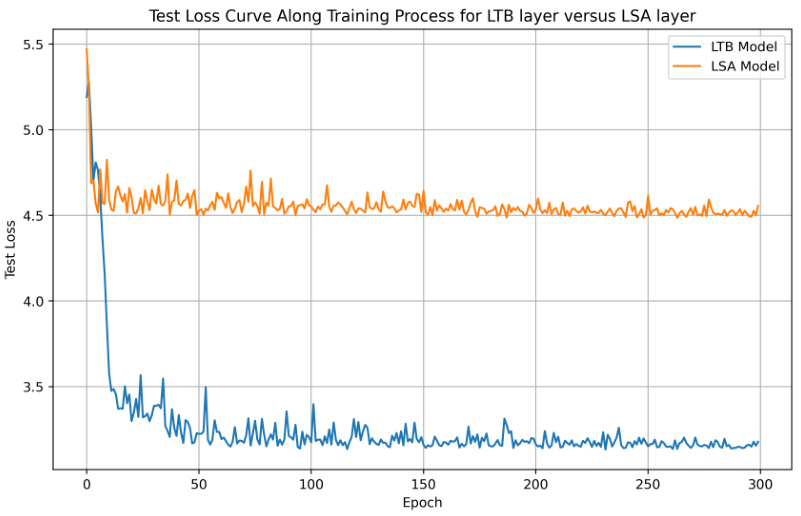
🔼 This figure shows the test loss curves of both LTB and LSA models during the training process. The x-axis represents the training epoch, and the y-axis represents the test loss. As shown, the LTB model converges to a lower test loss compared to the LSA model, suggesting its superior performance in ICL of linear regression with a shared signal.
read the caption
Figure 1: The test loss along the training process for LTB and LSA layer.
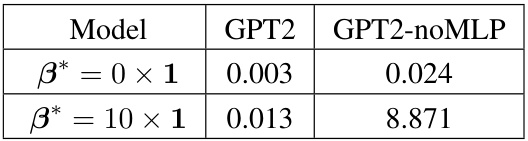
🔼 This table presents the results of experiments conducted using GPT2 models with and without MLP components. The models were trained and tested on linear regression tasks with a shared signal, comparing their performance across two different settings: one where the mean of the task parameter (β*) is zero and another where β* is a vector of tens. The table shows the losses achieved by each model in each scenario, highlighting the performance differences between models with and without MLP layers when dealing with a non-zero mean in task parameters.
read the caption
Table 1: Losses of GPT2 with or without MLP component for linear regression with a shared signal.
Full paper#