↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Graph Class Incremental Learning (GCIL) faces the challenge of models ‘forgetting’ previously learned information when learning new classes. Existing methods try to alleviate forgetting but lack a clear understanding of what’s crucial to preserve. This paper argues that existing methods suffer from substantial semantic and structural shifts, hindering performance.
The proposed solution, Graph Spatial Information Preservation (GSIP), directly addresses these issues. GSIP preserves low-frequency information (aligning old and new node representations) and high-frequency information (mimicking old node similarity patterns) to calibrate these shifts. Experiments show GSIP significantly reduces forgetting (up to 10% improvement) compared to existing approaches across several large datasets. It’s also seamlessly compatible with existing replay methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the critical problem of catastrophic forgetting in graph class incremental learning (GCIL), a common challenge in real-world applications involving continuously evolving graph data. The proposed framework, GSIP, offers a novel solution with significant performance improvements, directly impacting researchers working on continual learning and graph neural networks. By providing theoretical insights and a practical framework, this work opens new avenues for research in efficient information preservation methods for handling dynamic graph data.
Visual Insights#

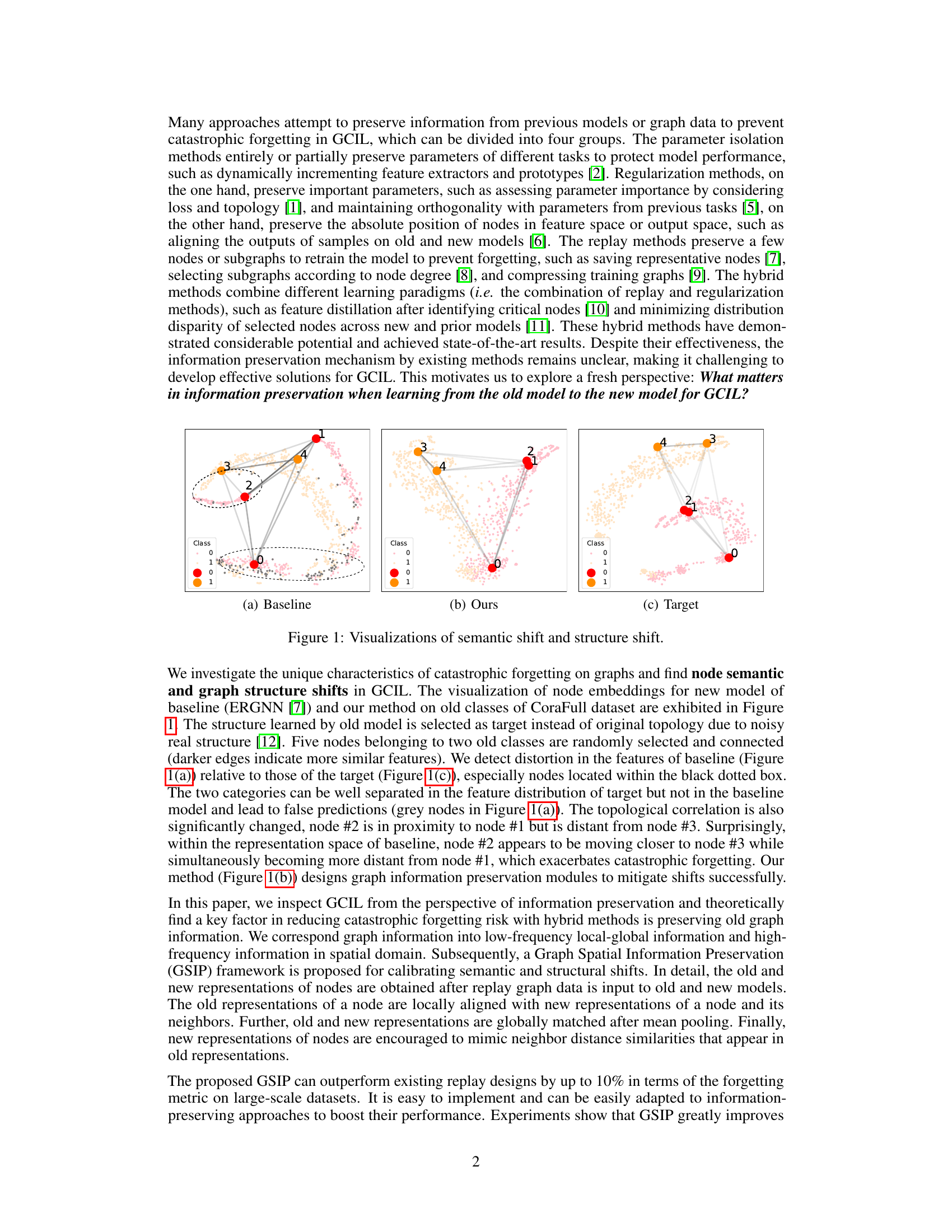
This figure visualizes the effects of catastrophic forgetting in graph class incremental learning (GCIL). It compares the node embeddings learned by a baseline model (ERGNN), the proposed GSIP method, and the desired target representation for old classes in the CoraFull dataset. The baseline shows significant distortion in node embeddings, indicating semantic and structural shifts, particularly in nodes within a black dotted box. This distortion leads to misclassification. In contrast, GSIP successfully mitigates these shifts, resulting in embeddings closer to the target. The figures illustrate how semantic and structural changes affect model performance during incremental learning, and GSIP’s success in reducing these changes.
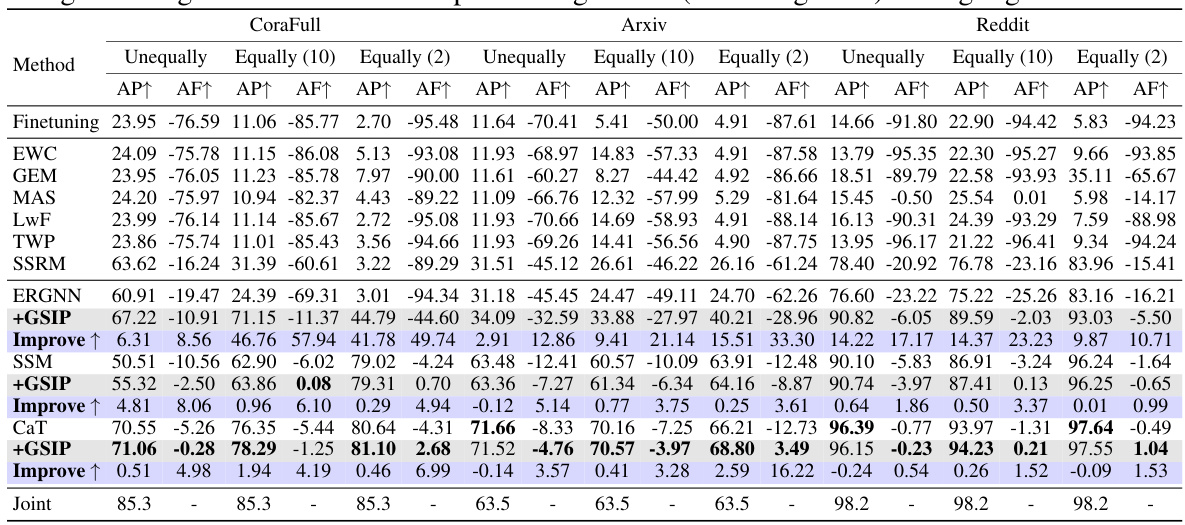
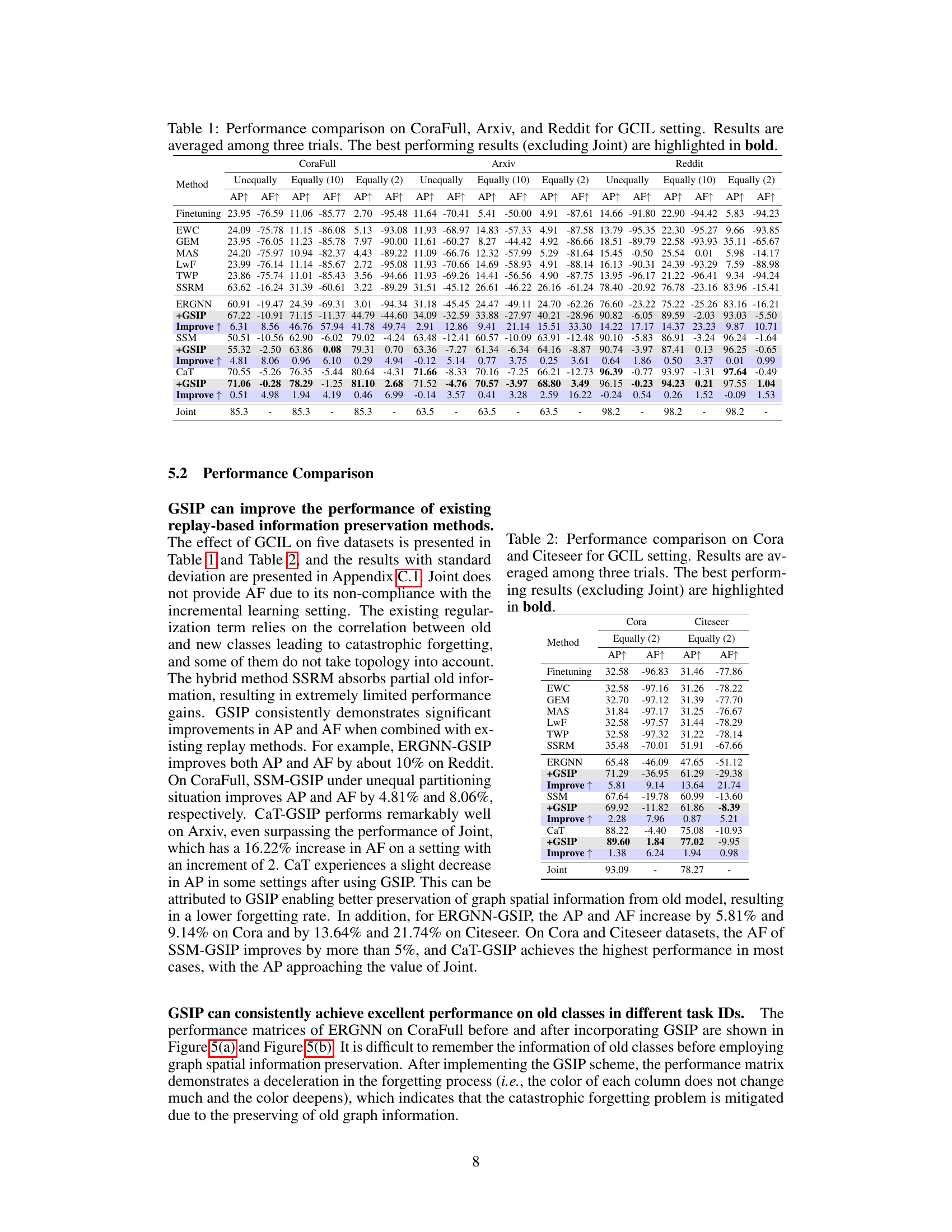
This table presents a comparison of the performance of different methods on three datasets (CoraFull, Arxiv, and Reddit) for the Graph Class Incremental Learning (GCIL) task. The results are shown for three different class partitioning scenarios: Unequally, Equally (10), and Equally (2). For each scenario and dataset, the table shows the Average Performance (AP) and Average Forgetting (AF) metrics. The best performing method for each scenario and dataset (excluding the ‘Joint’ method, which serves as an upper bound) is highlighted in bold. The table provides a quantitative comparison of various approaches to handling catastrophic forgetting in GCIL.
In-depth insights#
Graph Info Preservation#
The concept of “Graph Info Preservation” in incremental graph learning focuses on mitigating catastrophic forgetting, where the model loses information about previously learned classes when learning new ones. This is crucial because real-world graph data is often dynamic, with new nodes and edges constantly appearing. Effective preservation strategies maintain critical structural and semantic information from the older graph representation, ensuring that the model retains its ability to classify nodes from previous classes accurately. Different preservation methods exist, each focusing on different aspects of graph structure and node features. Key aspects of successful preservation involve capturing both low-frequency (global structure, long-range relationships) and high-frequency (local patterns, immediate node neighborhoods) information. Challenges include determining which information to preserve, balancing computational cost, and handling various graph structures and evolving data distributions. Ultimately, effective graph information preservation is vital for robust and adaptable graph learning systems in real-world scenarios.
Spatial Info Effects#
The heading ‘Spatial Info Effects’ suggests an investigation into how spatial relationships within data influence model performance and learning. A thoughtful analysis would explore how incorporating spatial information, such as distances between nodes in a graph or geographical coordinates, can improve model accuracy, robustness and generalization. Key aspects to consider include: the impact of different spatial representations (e.g., adjacency matrices vs. distance matrices) on model learning, the effectiveness of various spatial information integration techniques (e.g., graph convolutional networks, attention mechanisms), and the trade-offs between spatial accuracy and computational cost. Furthermore, a deeper dive should assess whether different types of spatial information impact different aspects of learning, particularly for scenarios with non-uniform spatial distributions or large-scale datasets. A well-rounded discussion should include a comparison against approaches that ignore or only implicitly consider spatial information, demonstrating the concrete benefits of an explicit spatial focus. Ultimately, a successful exploration should yield strong evidence to support the importance of incorporating spatial information for improved model design and performance.
GSIP Framework#
The GSIP (Graph Spatial Information Preservation) framework is a novel approach to address catastrophic forgetting in graph class incremental learning (GCIL). It leverages the idea that preserving crucial graph information from previous learning stages is key to mitigating the semantic and structural shifts that lead to forgetting. GSIP uniquely decomposes graph information into low-frequency (local-global) and high-frequency (spatial) components. The low-frequency component focuses on aligning old and new node representations, ensuring consistency between the old model’s output and the new model’s output for both individual nodes and aggregated neighborhood information. The high-frequency component aims at preserving the relative spatial similarities between nodes in the new model, replicating the topological relationships learned from previous stages. This dual-pronged approach ensures that both semantic and structural aspects of the graph are preserved. The framework’s simplicity and adaptability are highlighted by its seamless integration with existing replay mechanisms, demonstrating its potential for substantial performance improvements in GCIL.
Ablation Study#
An ablation study systematically evaluates the contribution of individual components within a machine learning model. In the context of a research paper, an ablation study section would typically detail experiments where parts of the model are removed or altered to isolate the impact of specific features. The results from these experiments offer crucial insights into the model’s design choices and overall effectiveness. A well-executed ablation study is vital for justifying design decisions, demonstrating the importance of each component, and identifying potential areas for improvement. It strengthens the paper’s claims by showing precisely what aspects lead to the observed performance. By methodically removing features and observing the resulting changes in performance, researchers can isolate the effects of each feature and build a more robust understanding of the model’s architecture. The results of such experiments should be presented clearly and concisely, often in tabular form, showing the relative importance of each component.
Future Works#
Future research directions stemming from this graph class incremental learning (GCIL) study could explore more sophisticated methods for information preservation, potentially moving beyond simple replay and towards techniques that more effectively capture the complex relationships within graph data. Investigating the impact of different graph structures and their effect on catastrophic forgetting is crucial. A deeper theoretical understanding of the interplay between low and high-frequency information preservation, and its relationship to semantic and structural shifts, would significantly enhance the field. Developing more robust and scalable algorithms capable of handling large-scale datasets and continuous streams of data is also important. Finally, the ethical implications, such as potential biases, and fairness concerns, especially in real-world applications of GCIL, deserve much more attention.
More visual insights#
More on figures

The figure visualizes the effects of catastrophic forgetting in graph class incremental learning (GCIL). It shows the node embeddings for three scenarios on the CoraFull dataset: (a) Baseline (ERGNN), (b) the proposed GSIP method, and (c) the target (desired) structure. Comparing (a) and (c) highlights the distortions caused by forgetting in the baseline approach, particularly evident in the black dotted box. The proposed method (b) demonstrates successful mitigation of these semantic and structural shifts.
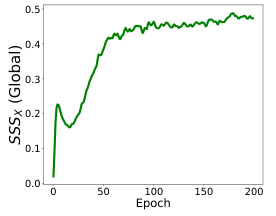
This figure shows the semantic shift (left) and structural shift (right) between the old and new models’ representations for the CoraFull dataset. The Semantic Shift Score (SSSx) measures the divergence in node-level semantics, while the Structural Shift Score (SSSA) quantifies changes in the graph-level structure. Both scores are plotted against the number of training epochs. The graphs demonstrate that both semantic and structural shifts increase gradually as the model learns new classes, highlighting the challenge of catastrophic forgetting in graph class incremental learning (GCIL).
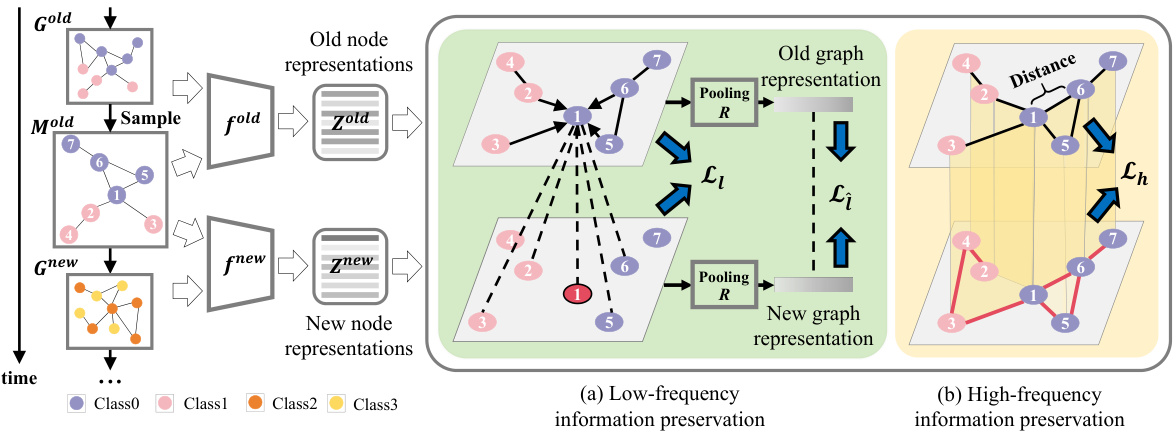
This figure illustrates the GSIP (Graph Spatial Information Preservation) framework, which is composed of two main modules: low-frequency and high-frequency information preservation. The low-frequency module aligns old node representations with new node and neighbor representations, followed by global matching of old and new outputs. The high-frequency module encourages new node representations to mimic the near-neighbor similarity of old representations. Both modules aim to preserve old graph information, thereby calibrating semantic and structural shifts during incremental learning.

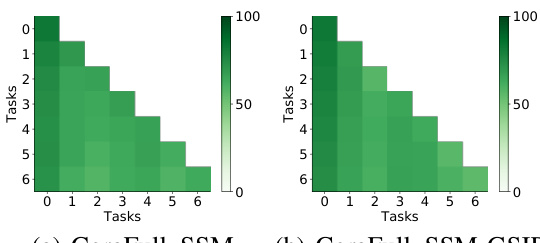
Figure 5 presents four subfigures that illustrate different aspects of the proposed Graph Spatial Information Preservation (GSIP) method. (a) and (b) show performance matrices for ERGNN and ERGNN-GSIP, respectively, visualizing the model’s performance on various tasks. (c) shows the calibration of semantic and structural shifts over epochs, highlighting how GSIP mitigates these shifts. Finally, (d) analyzes the impact of the number of stored nodes (#M) on performance, demonstrating the efficiency of GSIP even with limited memory.

This figure visualizes the performance of the proposed GSIP method and the baseline ERGNN method on the CoraFull dataset. Subfigure (a) and (b) shows the performance matrices of ERGNN and ERGNN-GSIP, respectively, which are heatmaps representing the model’s performance on previous tasks after each new task increment. Subfigure (c) plots the semantic shift score (SSS) and structural shift score (SSSA) over training epochs, illustrating the shift calibration achieved by GSIP. Subfigure (d) shows the effect of the number of memory nodes (#M) on the performance of GSIP.

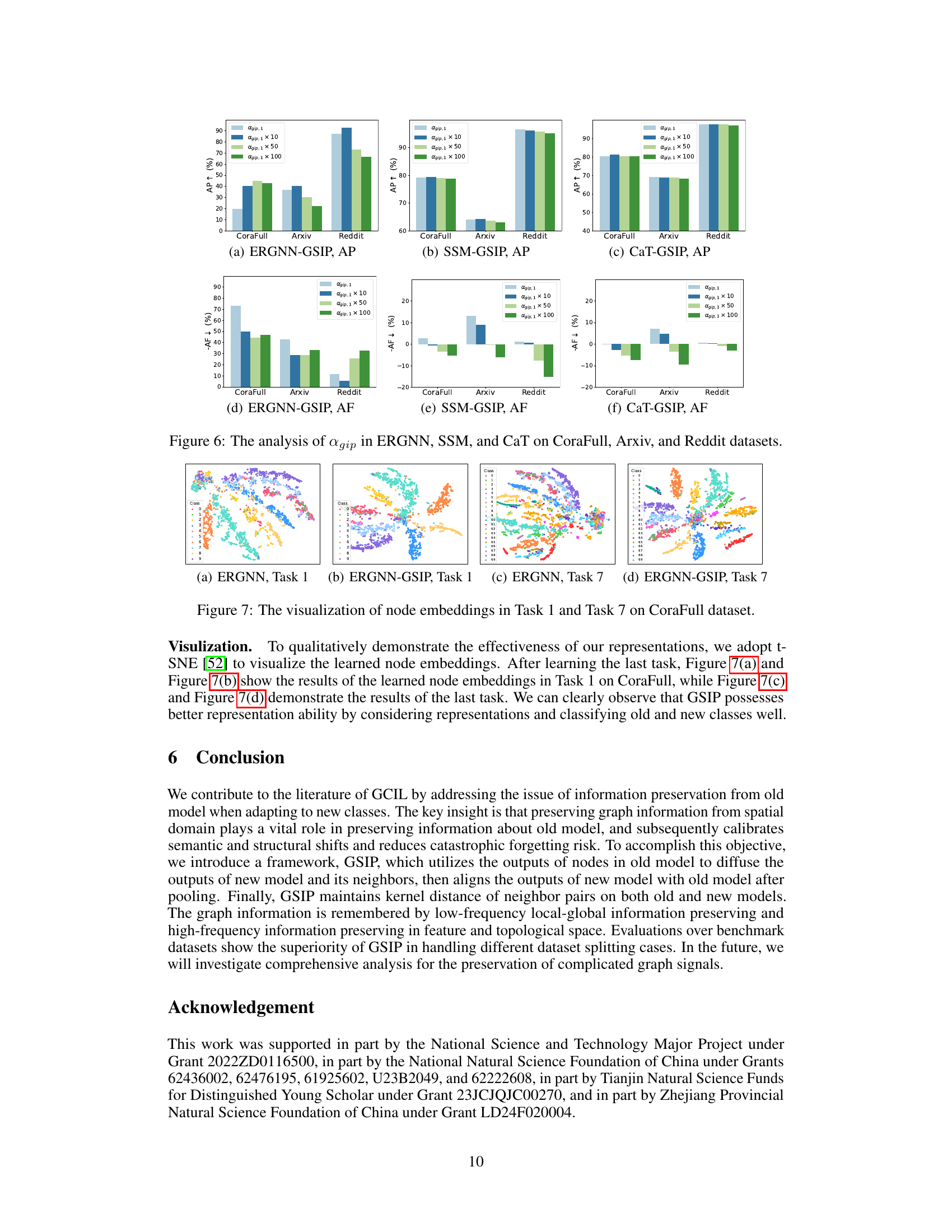
This figure visualizes the node embeddings learned by ERGNN and ERGNN-GSIP in Task 1 and Task 7 of the CoraFull dataset using t-SNE. The visualizations demonstrate that ERGNN-GSIP, by incorporating graph spatial information preservation, learns node embeddings that allow for better separation and classification of nodes, especially in later tasks (Task 7), indicating improved performance in handling catastrophic forgetting.
This figure shows four sub-figures. (a) and (b) are performance matrices of ERGNN and ERGNN-GSIP respectively on the CoraFull dataset. (c) demonstrates the semantic and structural shift calibration of the old and new models during the incremental process. Finally, (d) illustrates how the number of storage nodes (#M) impacts the performance of the proposed method.

This figure visualizes the characteristics of catastrophic forgetting on graphs, specifically focusing on node semantic and graph structure shifts in GCIL. It displays node embeddings for new models using the baseline (ERGNN) and the proposed method on old classes of the CoraFull dataset. The visualization highlights distortions in features for the baseline compared to the target, showing how the two categories are well-separated in the target’s feature distribution, but not in the baseline model. This ultimately illustrates the impact of semantic and structural shifts on classification accuracy and model performance.

This figure shows four subfigures. (a) and (b) show performance matrices of ERGNN and ERGNN-GSIP respectively on CoraFull dataset. These matrices visualize the model’s performance on old and new classes across multiple incremental learning tasks. (c) plots the semantic and structural shifts during the incremental learning process. The decrease in shift scores over time indicates that GSIP effectively maintains old information. (d) illustrates the impact of the number of stored nodes (#M) on the model’s performance, demonstrating that even with fewer nodes GSIP still maintains good performance.

This figure visualizes the performance of the proposed GSIP method and baseline models (ERGNN, SSM, CaT) across different tasks on the CoraFull dataset. Subfigures (a) and (b) show performance matrices, illustrating how well the models maintain performance on old classes as new classes are added. Subfigure (c) shows how semantic and structural shifts (metrics developed in the paper to quantify catastrophic forgetting) change over time, demonstrating that GSIP calibrates these shifts. Subfigure (d) analyzes the impact of the hyperparameter #M (the number of nodes stored in memory) on performance, showing that GSIP is robust to changes in this parameter.

This figure shows four subfigures. (a) and (b) are performance matrices for ERGNN and ERGNN-GSIP, respectively, on the CoraFull dataset. These matrices visualize the model’s performance on each class across multiple incremental learning tasks. (c) plots the semantic and structural shift scores over epochs, illustrating how the proposed method (GSIP) effectively mitigates these shifts. Finally, (d) illustrates how the model performance changes when varying the number of storage nodes (#M).
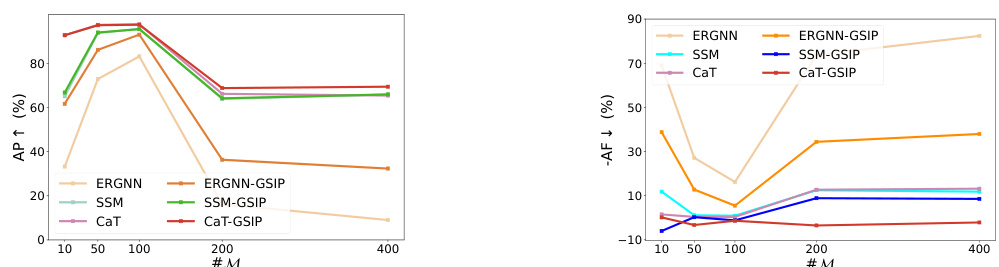
This figure presents four subplots illustrating different aspects of the proposed Graph Spatial Information Preservation (GSIP) method’s performance. (a) and (b) show performance matrices for ERGNN (without GSIP) and ERGNN-GSIP respectively, visualizing the model’s ability to retain information about old classes across multiple incremental learning tasks. (c) plots semantic and structural shift scores over epochs, showcasing how GSIP mitigates the catastrophic forgetting problem by calibrating these shifts. Finally, (d) demonstrates the impact of memory size (#M) on performance.
This figure shows four sub-figures that illustrate different aspects of the proposed GSIP method. (a) and (b) are performance matrices, which visualize the model’s performance across various tasks and how well it remembers old classes before and after applying GSIP respectively. (c) depicts the semantic and structural shifts during the incremental learning process, showing how GSIP helps calibrate these shifts. Finally, (d) analyzes the effect of the hyperparameter #M (number of nodes in memory) on model performance.

This figure consists of four subfigures. (a) and (b) show performance matrices for ERGNN and ERGNN-GSIP, respectively, illustrating the effectiveness of GSIP in preserving information from old models. (c) demonstrates the calibration of semantic and structural shifts by GSIP during incremental learning, showing that GSIP effectively reduces these shifts. (d) shows the impact of the number of stored nodes (#M) on model performance. Overall, this figure demonstrates the ability of GSIP to improve model performance and mitigate catastrophic forgetting in graph class incremental learning.

This figure presents four subplots visualizing different aspects of the proposed Graph Spatial Information Preservation (GSIP) method. Subplots (a) and (b) show performance matrices for ERGNN and ERGNN-GSIP respectively, which are visualizations of how well the models perform on different tasks across increments. Subplot (c) shows the semantic and structural shifts during increments, illustrating how GSIP calibrates these shifts. Subplot (d) illustrates the impact of the number of storage nodes (#M) on model performance, showing that GSIP performs consistently well even with fewer memory resources.

This figure visualizes the semantic and structural shifts observed in graph class incremental learning (GCIL). It compares node embeddings for old classes in a baseline method (ERGNN) versus the proposed GSIP method. The baseline shows significant distortion in node embeddings and class separation compared to the target structure (indicating catastrophic forgetting). The GSIP method shows much better preservation of the original structure and class separation. This illustrates the concept of node semantic and graph structure shifts as a key problem in GCIL that GSIP attempts to address.
More on tables
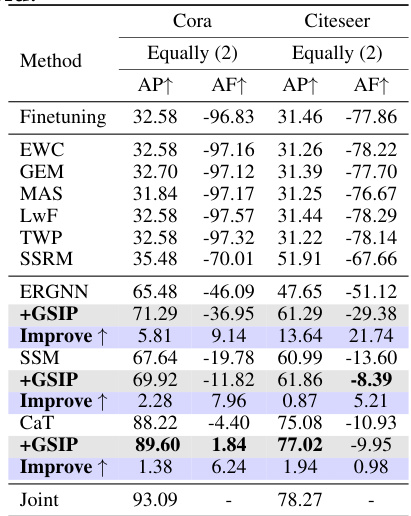
This table presents the performance comparison of different methods for graph class incremental learning (GCIL) on the Cora and Citeseer datasets. The results are averaged over three trials. The ‘AP↑’ column shows the average performance improvement, and the ‘AF↑’ column represents the average forgetting reduction. The best-performing methods (excluding the ‘Joint’ method, which serves as an upper bound) are highlighted in bold. Standard deviations are shown in gray to indicate variability in performance across different trials.

This table presents a comparison of the performance of various methods on three datasets (CoraFull, Arxiv, and Reddit) for the task of graph class incremental learning (GCIL). The performance is measured using two metrics: Average Performance (AP) and Average Forgetting (AF). The table shows results for different class partitioning strategies (unequal, equal with 10 classes per task, equal with 2 classes per task). The best performing model for each setting is highlighted in bold, excluding the ‘Joint’ method (which serves as an upper bound but isn’t a practical incremental learning method). The results demonstrate how GSIP improves the performance of existing methods.

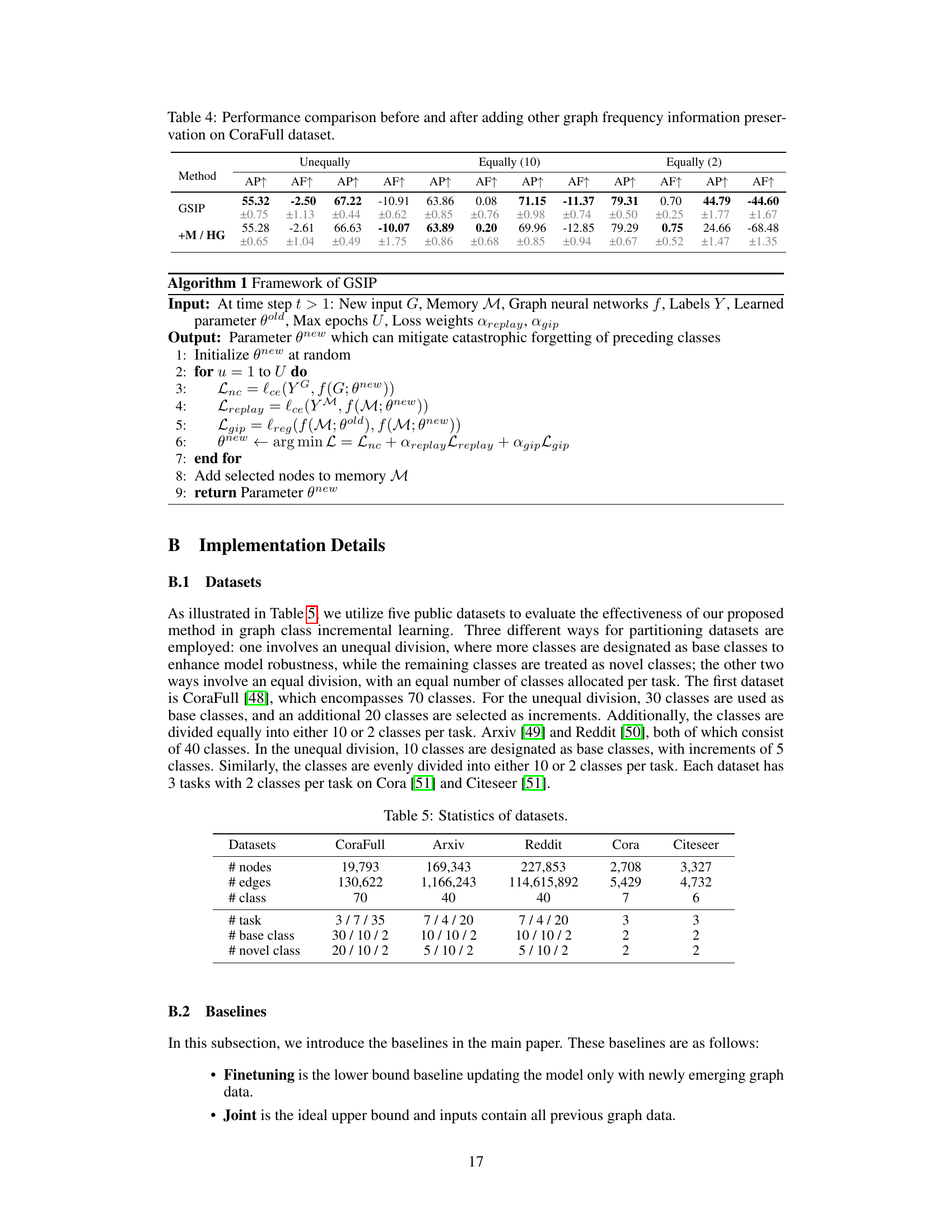
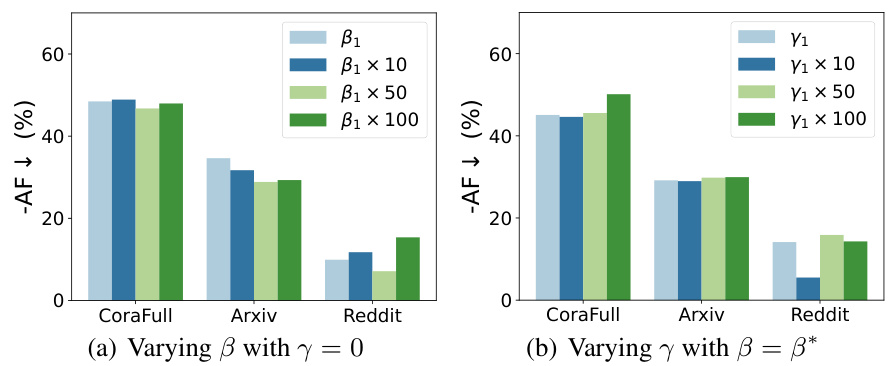
This table presents the ablation study results on the CoraFull dataset, comparing the performance of the GSIP model with different combinations of low-frequency local, low-frequency global, and high-frequency information preservation modules. It shows the Average Performance (AP) and Average Forgetting (AF) for different configurations of the GSIP model across three different experimental settings (Unequally, Equally(10), Equally(2)). The results highlight the contribution of each module to the overall performance of the model and illustrate how the inclusion of various frequency components enhances the model’s ability to preserve information and reduce catastrophic forgetting.

This table presents the characteristics of five datasets used in the paper’s experiments: CoraFull, Arxiv, Reddit, Cora, and Citeseer. For each dataset, it shows the number of nodes and edges, the total number of classes, the number of tasks (incremental learning steps), the number of base classes (classes present from the start), and the number of novel classes (new classes introduced in each incremental learning step). Different class partitioning schemes are used: unequal, equally (10 classes per task), and equally (2 classes per task) to simulate different learning scenarios. This detailed information provides context for understanding the experimental results and the challenges involved in the graph class incremental learning (GCIL) task.

This table presents a comparison of the performance of different methods on three datasets (CoraFull, Arxiv, and Reddit) for the task of graph class incremental learning (GCIL). The performance is measured by two metrics: Average Performance (AP) and Average Forgetting (AF). The table shows the results for three different experimental settings: unequal class partitioning, equal class partitioning with 10 classes per task, and equal class partitioning with 2 classes per task. The best-performing methods (excluding the Joint method, which serves as an upper bound) are highlighted in bold for each setting.
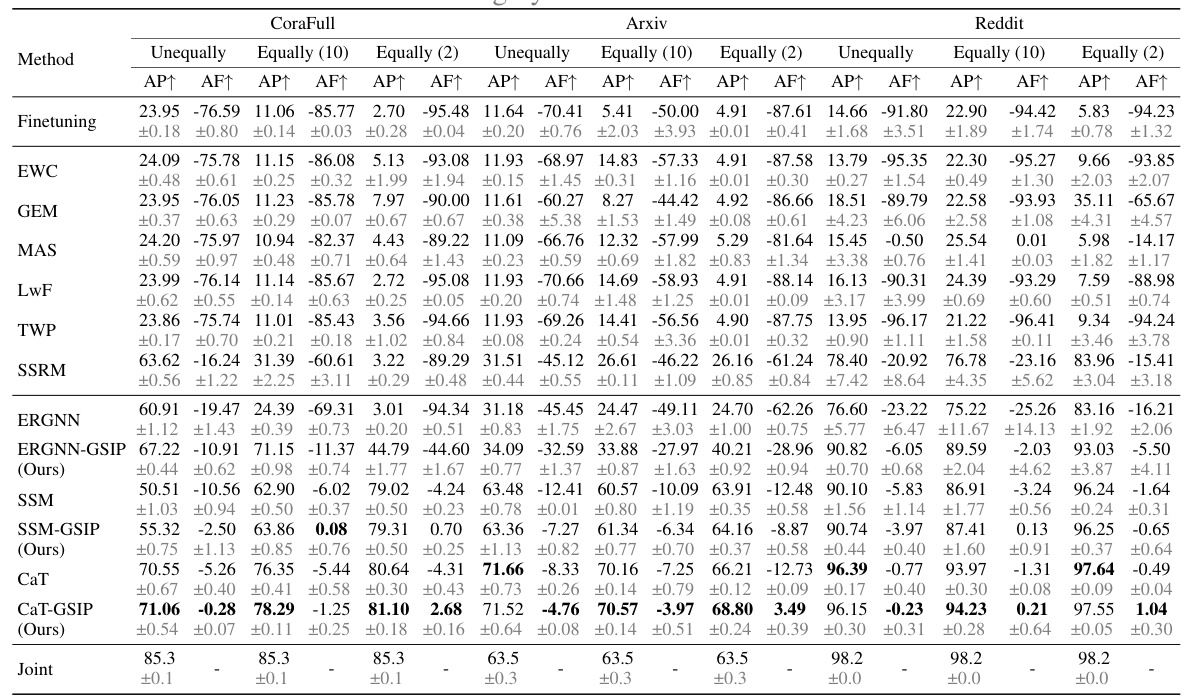
This table presents a comparison of different methods for graph class incremental learning (GCIL) on three benchmark datasets: CoraFull, Arxiv, and Reddit. The results show the average performance (AP) and average forgetting (AF) for each method across three experimental trials. The best performing method for each dataset and setting (excluding the ‘Joint’ method, which serves as an upper bound) is highlighted in bold. The table allows for a comparison of performance across various GCIL approaches and datasets under different class partitioning schemes (unequal, equally 10 classes, equally 2 classes).

This table presents a comparison of the performance of different methods for graph class incremental learning (GCIL) on three datasets: CoraFull, Arxiv, and Reddit. The performance is measured using two metrics: Average Performance (AP) and Average Forgetting (AF). The table shows the AP and AF for each method under different experimental conditions (unequal class partitioning, equal partitioning with 10 classes per task, and equal partitioning with 2 classes per task). The best-performing method (excluding the ‘Joint’ method, which serves as an upper bound by using all data) is highlighted in bold for each condition.

This table presents a performance comparison of various methods on three datasets (CoraFull, Arxiv, and Reddit) using the Graph Class Incremental Learning (GCIL) setting. Results include Average Performance (AP) and Average Forgetting (AF), with the best performing methods (excluding the ‘Joint’ method, which serves as an upper bound) highlighted in bold. Standard deviations are also shown in gray, providing insight into the variability of the results.
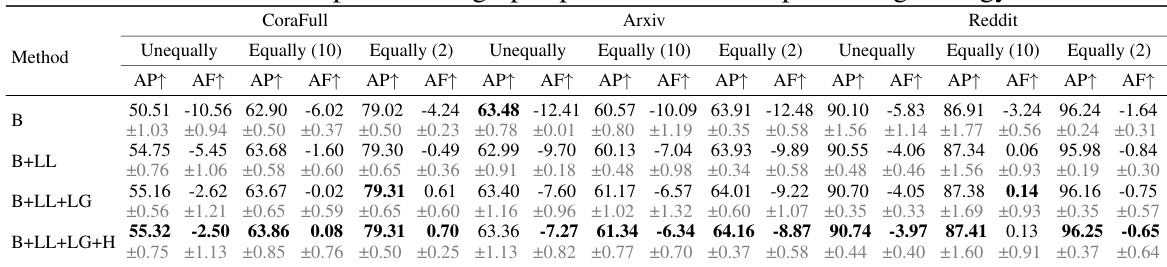
This table presents a comparison of the performance of different methods for Graph Class Incremental Learning (GCIL) on three datasets: CoraFull, Arxiv, and Reddit. The performance is evaluated using two metrics: Average Performance (AP) and Average Forgetting (AF). The table shows the results for three different class partitioning strategies: Unequal, Equally (10), and Equally (2). The best performing models (excluding the ‘Joint’ model, which serves as an upper bound) are highlighted in bold. The results are averages across three trials, and the standard deviations are shown in grey in the original paper.

This table presents the ablation study results for the ERGNN model. It shows the average performance (AP) and average forgetting (AF) metrics, along with their standard deviations, for different configurations of the GSIP framework. The configurations vary by including or excluding low-frequency local (LL), low-frequency global (LG), and high-frequency (H) information preservation modules. The results are broken down by dataset (CoraFull, Arxiv, Reddit) and class partitioning scheme (unequal, equally (10), equally (2)). The baseline (B) performance is compared against the improvements achieved by adding each module sequentially.

This table shows the running time in seconds for each epoch under three different dataset partitioning scenarios (Unequally, Equally (10), Equally (2)) for several methods: ERGNN, ERGNN with GSIP, SSM, SSM with GSIP, CaT, and CaT with GSIP. The results highlight the computational cost of each method across various data partitioning strategies on the CoraFull dataset.
Full paper#