Adaptive Variance Reduction for Stochastic Optimization under Weaker Assumptions

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in stochastic optimization because it presents novel adaptive variance reduction methods that achieve optimal convergence rates under weaker assumptions than existing techniques. This opens new avenues for developing more efficient and robust optimization algorithms across various applications, including machine learning and beyond. The results are particularly important for researchers working on non-convex problems, where optimal convergence is often challenging to achieve.

Visual Insights

#

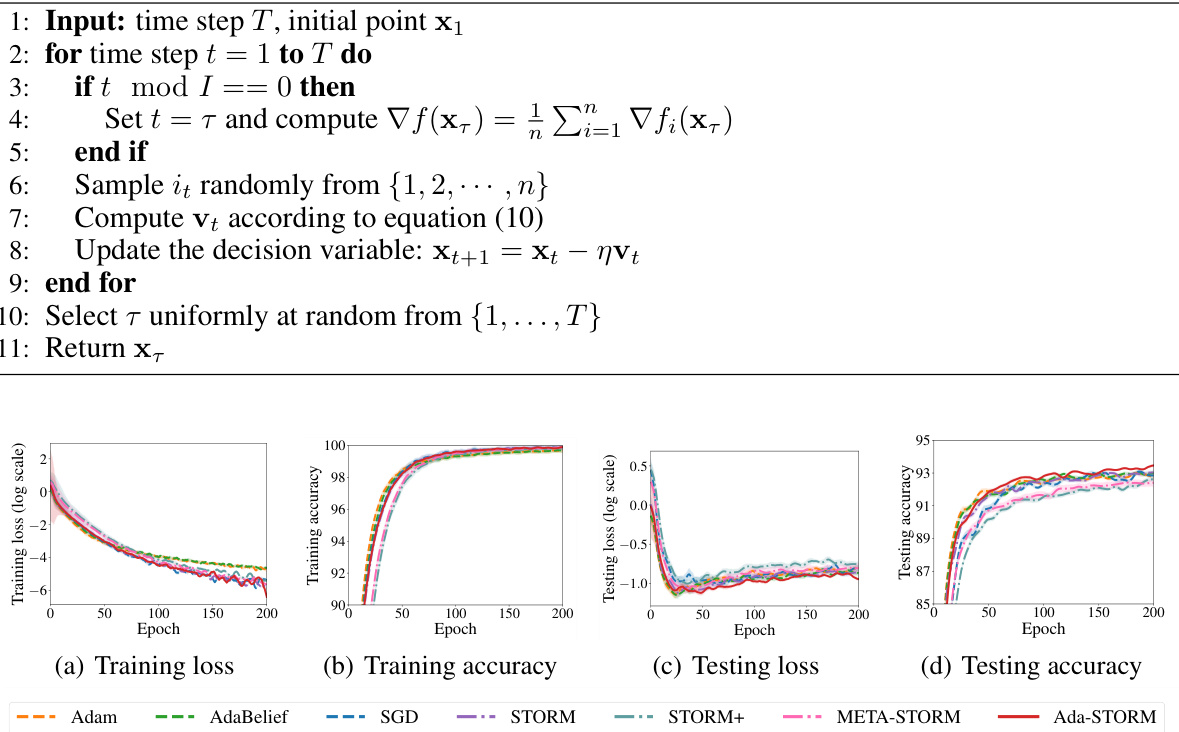
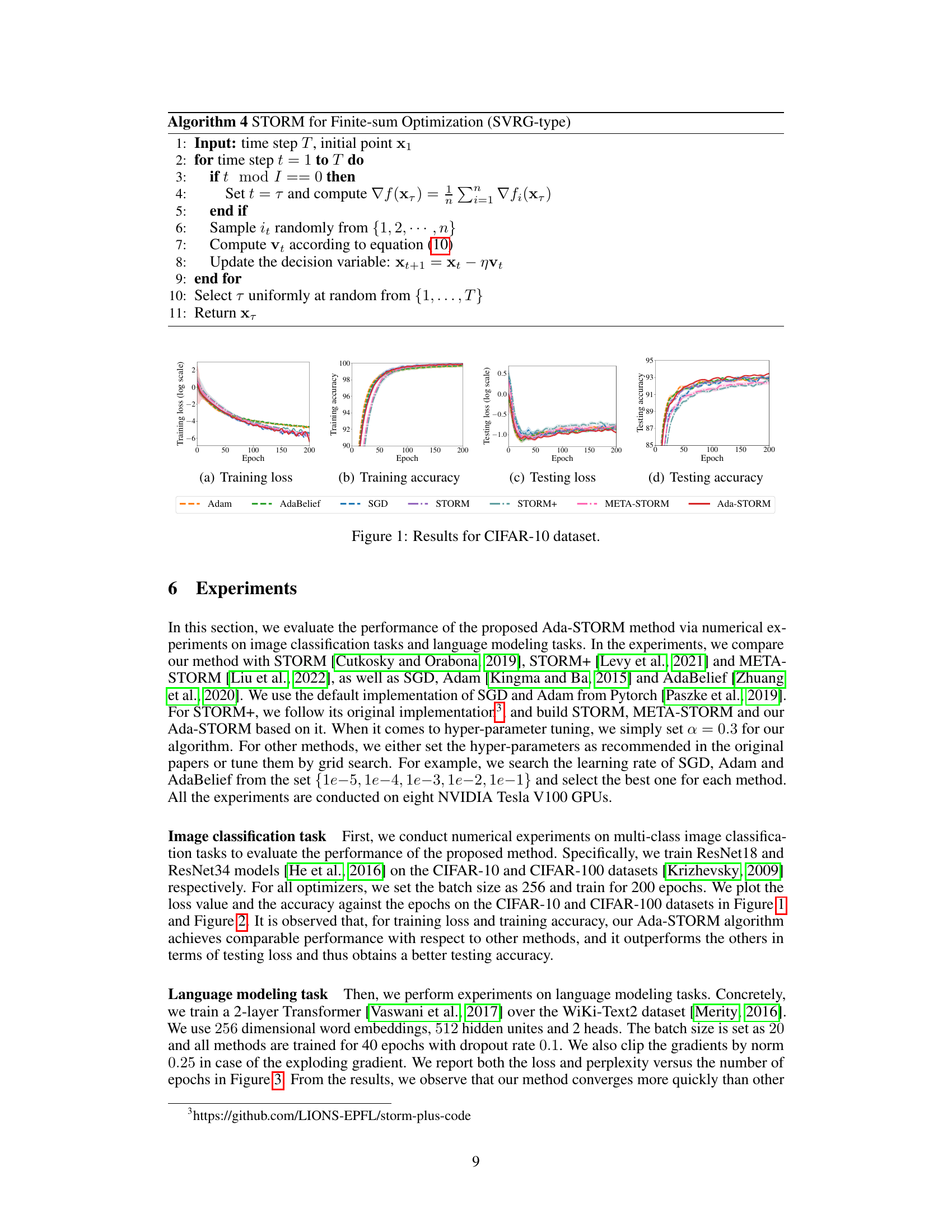
The figure shows the training and testing performance of different optimization algorithms on the CIFAR-10 dataset. The algorithms compared include Adam, AdaBelief, SGD, STORM, STORM+, META-STORM, and the proposed Ada-STORM. The plots show training loss, training accuracy, testing loss, and testing accuracy over 200 epochs. The results illustrate the comparative performance of the algorithms in terms of convergence speed and final accuracy.

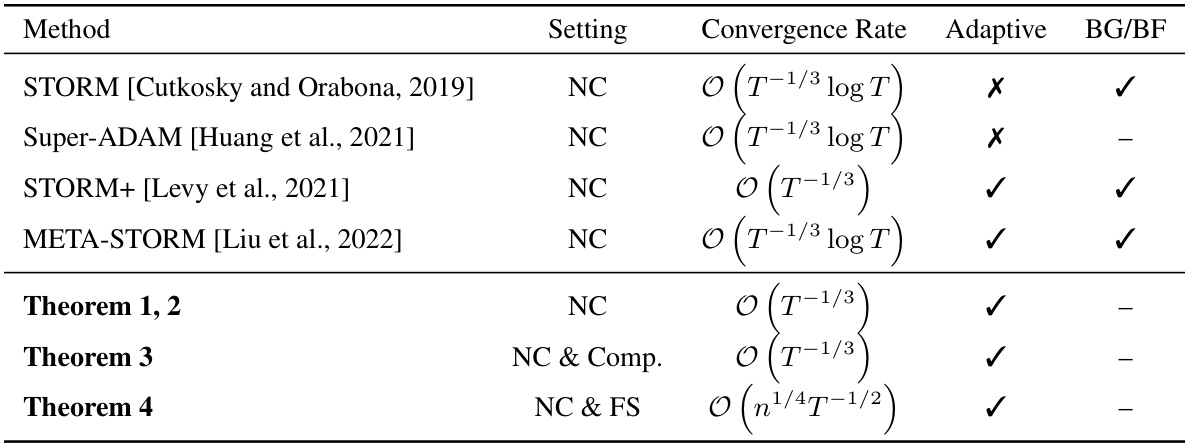
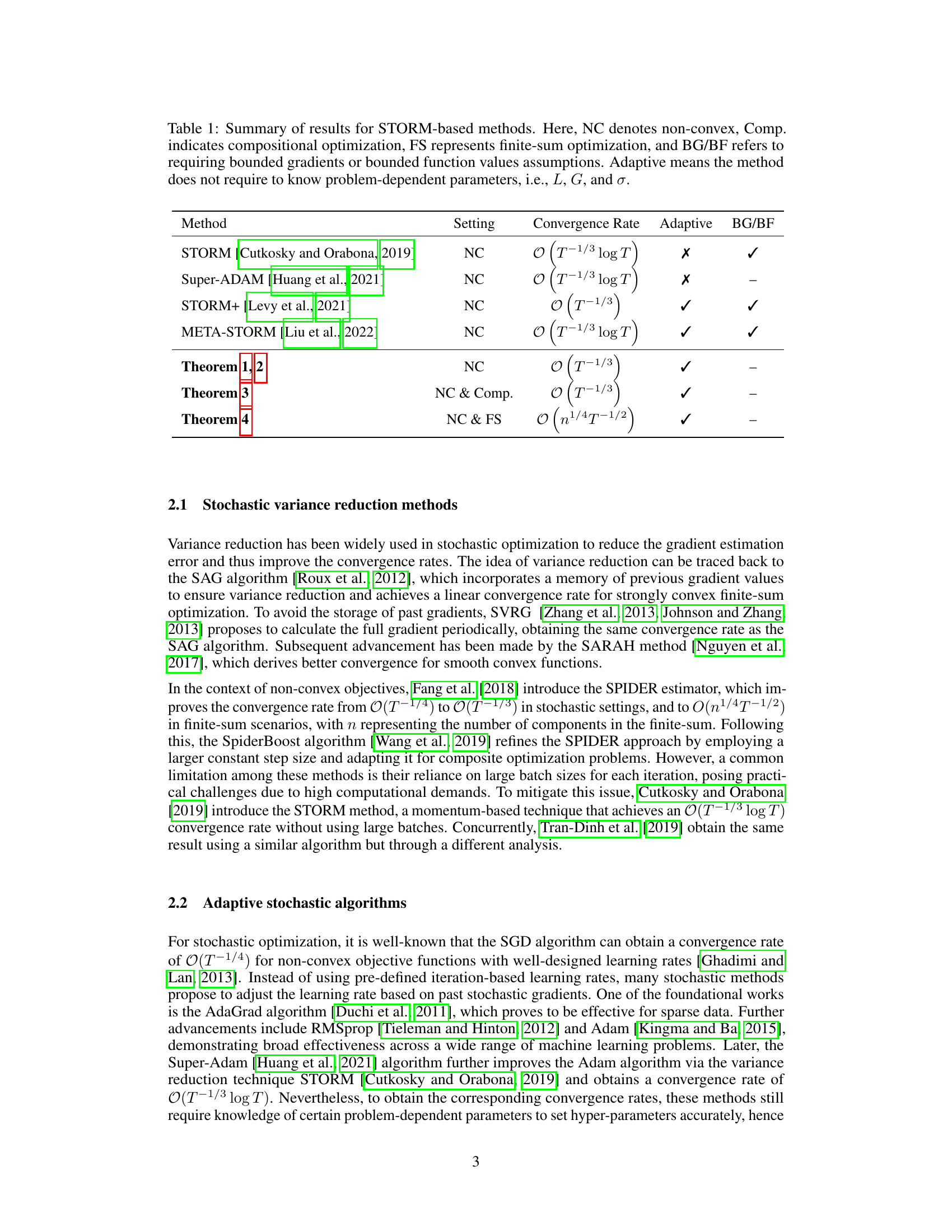
This table summarizes the convergence rates achieved by various STORM-based methods for different optimization settings (non-convex, compositional, finite-sum). It also indicates whether each method is adaptive (does not require prior knowledge of problem-dependent parameters) and the assumptions made regarding bounded gradients or function values.

In-depth insights

#

Adaptive STORM

#

The concept of “Adaptive STORM” in the context of stochastic optimization is a significant advancement. It addresses the limitations of traditional STORM methods by removing the need for strong assumptions like bounded gradients and function values, which are often unrealistic in real-world applications. The core innovation lies in the adaptive learning rate strategy, dynamically adjusting the learning rate based on the observed stochastic gradients. This eliminates the reliance on pre-defined hyperparameters and allows the algorithm to automatically adapt to the problem’s characteristics. By achieving an optimal convergence rate without additional logarithmic terms, Adaptive STORM shows that it is possible to achieve high-performance stochastic optimization while keeping the requirements for prior knowledge of the problem to a minimum. The extension to stochastic compositional optimization and non-convex finite-sum problems further highlights the method’s versatility and broad applicability. The use of a doubling trick effectively manages the computational needs of the method. Overall, Adaptive STORM presents a highly effective and flexible solution for a wide range of stochastic optimization problems, marking a considerable step forward in the field.

Optimal Rates

#

The concept of “Optimal Rates” in stochastic optimization algorithms refers to the best possible convergence speed achievable under specific assumptions. A method achieving an optimal rate guarantees that no other algorithm can significantly outperform it, given the same constraints. Understanding the assumptions underlying these rates is crucial; stronger assumptions (e.g., bounded gradients, strong convexity) often lead to faster rates but limit applicability. Adaptive methods aim to achieve optimal rates without prior knowledge of problem-dependent parameters, making them more practical. The paper likely explores optimal rates for non-convex problems, potentially showcasing how variance reduction techniques or clever learning rate scheduling help reach the theoretical limits. The optimal rate attained provides a benchmark, helping evaluate the efficiency of various algorithms and motivating further research in improving upon these theoretical bounds, particularly in challenging scenarios where assumptions are relaxed.

Compositional Opt.

#

Compositional optimization tackles problems where the objective function is a composition of multiple functions, often involving nested structures or stochasticity. It’s a challenging area because standard optimization techniques often struggle with the complex dependencies between the nested functions. Effective methods need to handle the propagation of gradients and uncertainties through the composition, often requiring specialized variance reduction techniques or specific assumptions on function properties. Adaptive methods, which automatically adjust parameters based on observed data, are particularly valuable for compositional optimization, since problem-specific parameters are often unknown or difficult to estimate. The optimal convergence rates for non-convex compositional problems are typically slower than their single-function counterparts, highlighting the inherent difficulty of the problem. Research in this area focuses on developing efficient algorithms with optimal or near-optimal convergence rates under weaker assumptions, aiming for practical applicability. Future work might explore more robust adaptive methods that are less sensitive to noisy estimations or assumptions about the individual component functions, addressing practical challenges and extending applicability to broader real-world problems.

Finite-Sum Case

#

The finite-sum case in stochastic optimization, where the objective function is a sum of individual component functions, presents unique challenges and opportunities. Variance reduction techniques are particularly valuable in this setting, as they can significantly reduce the variance of the stochastic gradient estimates. The paper explores an adaptive variance reduction method tailored for the finite-sum case, achieving an optimal convergence rate of O(n^(1/4)T^(-1/2)). This result improves upon existing adaptive methods by removing the additional O(log(nT)) term, indicating a more efficient approach. The core idea involves incorporating an additional term in the STORM estimator that leverages past gradients to further reduce variance. This modification, coupled with a carefully designed adaptive learning rate, enables the method to achieve the optimal rate without requiring prior knowledge of problem-dependent parameters like smoothness or gradient bounds. The adaptive nature of this approach is crucial, allowing it to automatically adjust to the characteristics of the problem and data without manual tuning. This adaptive approach demonstrates superior numerical performance, confirming its effectiveness in practical settings.

Future Research

#

Future research directions stemming from this work could explore several promising avenues. Extending the adaptive variance reduction methods to other non-convex optimization problems beyond the ones considered (e.g., constrained optimization, minimax problems) would be highly valuable. Investigating the theoretical limits of adaptive methods and whether tighter bounds are achievable is a crucial theoretical question. Developing more robust adaptive learning rate strategies that are less sensitive to hyperparameter tuning or initial conditions would increase practical applicability. Finally, empirical evaluations on a wider range of real-world datasets and tasks would help assess the generalizability and practical effectiveness of the proposed approach across diverse problem domains. The robustness of the methodology to noisy data, high-dimensionality, and the effects of different dataset characteristics are all areas ripe for further study.

More visual insights

#

More on figures

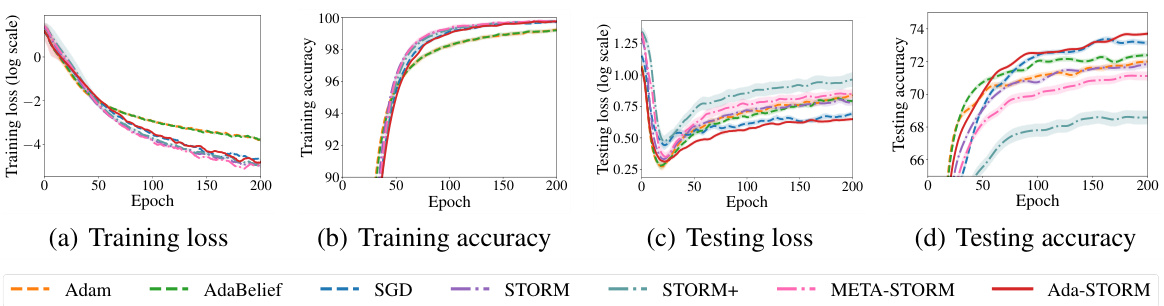
This figure presents the results of the CIFAR-10 image classification experiment. It shows four subplots: training loss, training accuracy, testing loss, and testing accuracy. Each subplot displays the performance of various optimization methods (Adam, AdaBelief, SGD, STORM, STORM+, META-STORM, and Ada-STORM) over 200 epochs. The x-axis represents the epoch number, and the y-axis represents the corresponding metric (loss or accuracy). Error bars are included to indicate the variability of the results. Ada-STORM shows promising performance in testing accuracy.

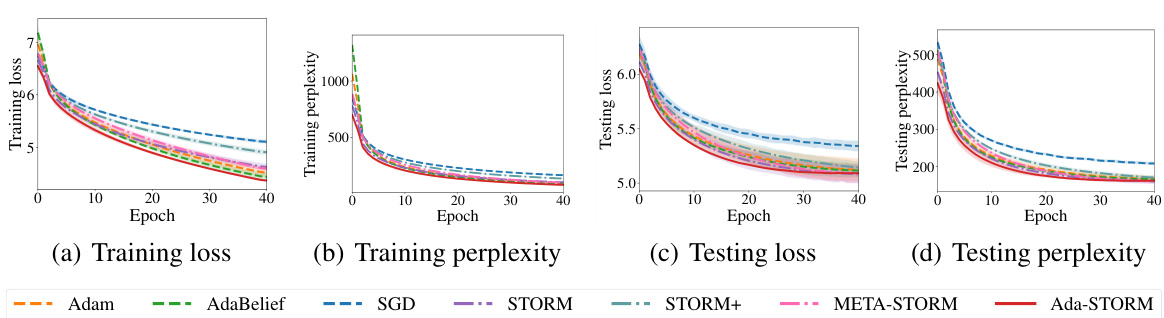
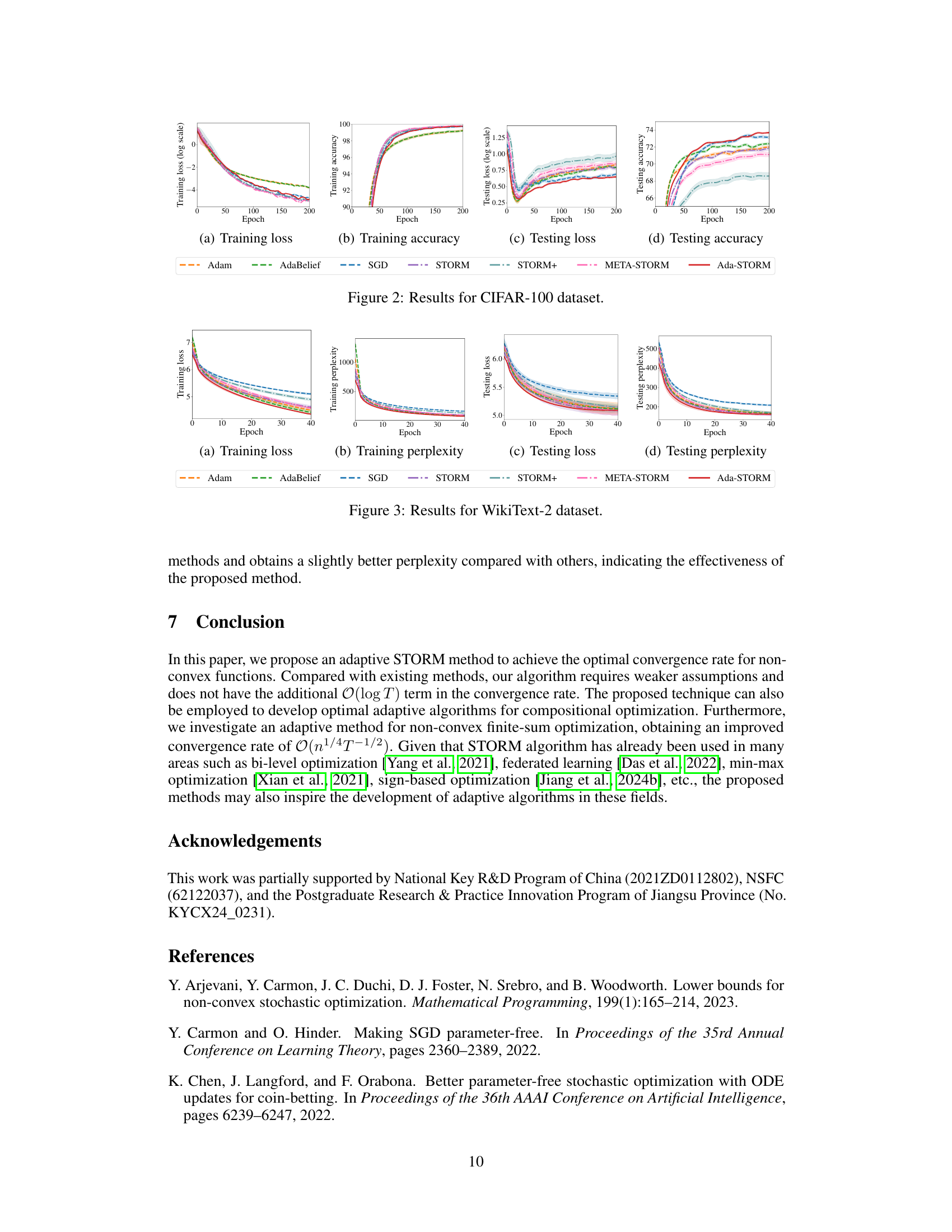
The figure shows the results of training a 2-layer Transformer language model on the WikiText-2 dataset using various optimization methods. The plots show training and testing loss and perplexity over 40 epochs. The methods compared are Adam, AdaBelief, SGD, STORM, STORM+, META-STORM, and Ada-STORM. Ada-STORM demonstrates comparable performance for training loss and accuracy to other methods, but outperforms others in testing loss, which indicates better generalization ability.

More on tables

This table summarizes the convergence rates and assumptions of various STORM-based methods for non-convex, compositional, and finite-sum optimization problems. It compares the methods’ convergence rates (O(T−1/3logT), O(T−1/3), etc.), indicating whether they are adaptive (requiring no prior knowledge of problem-specific parameters), and whether they require bounded gradients or function values. The table highlights the improvements achieved by the proposed Ada-STORM method in terms of weaker assumptions and optimal convergence rates.

This table compares different STORM-based methods in terms of their convergence rates, assumptions (bounded gradients/function values), and whether they are adaptive (i.e., do not require problem-dependent parameters). It summarizes the key findings of the paper regarding the performance of various methods for solving non-convex optimization problems, including standard, compositional, and finite-sum cases.

This table summarizes the convergence rates achieved by various STORM-based methods for different optimization settings (non-convex, compositional, finite-sum). It highlights whether each method requires strong assumptions like bounded gradients or function values, and indicates if the method is adaptive (does not need problem-dependent hyperparameters).

Full paper

#