Inversion-based Latent Bayesian Optimization

TrN5TcWY87

Jaewon Chu et el.

TL;DR
#

Latent Bayesian Optimization (LBO) is a powerful technique for tackling optimization challenges in complex spaces, but current LBO methods suffer from a ‘misalignment problem’ caused by reconstruction errors. This problem leads to inaccurate surrogate models and poor-quality solutions. Existing solutions attempt to correct the misalignment problem through re-centering, but these methods are inefficient as they require a huge number of additional function evaluations.

This paper introduces Inversion-based Latent Bayesian Optimization (InvBO), a novel plug-and-play module that directly tackles the misalignment problem. InvBO consists of two key components: an inversion method to precisely recover the latent codes that reconstruct the data, and a potential-aware trust region anchor selection that strategically chooses the center of the trust region to enhance the optimization process. InvBO demonstrates significant performance gains across several real-world tasks and is shown to be effective on various benchmarks. Importantly, InvBO is a plug-and-play module so can be implemented to improve performance of multiple existing LBO methods.

Key Takeaways
#

Why does it matter?
#

This paper is crucial for researchers in Bayesian Optimization and related fields because it directly addresses a significant limitation of existing Latent Bayesian Optimization (LBO) methods—the misalignment problem. InvBO offers a novel, efficient solution, improving the accuracy and efficiency of LBO, thereby impacting numerous applications relying on efficient optimization in high-dimensional spaces. It opens new avenues for research by introducing a plug-and-play module easily integrated into existing LBO frameworks, and its theoretical analysis provides a solid foundation for future advancements in the field. The demonstrated improvements across various real-world benchmarks further highlight its practical value and broad applicability.

Visual Insights
#

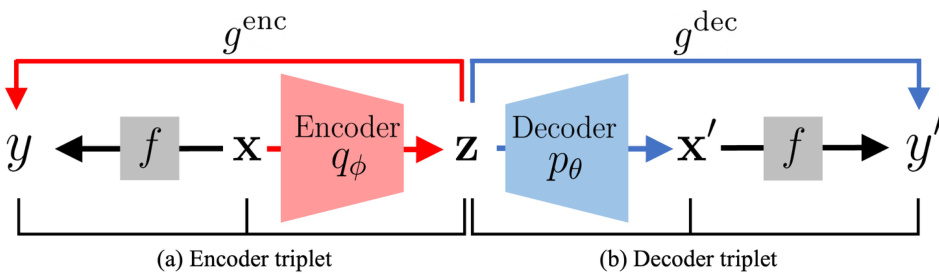
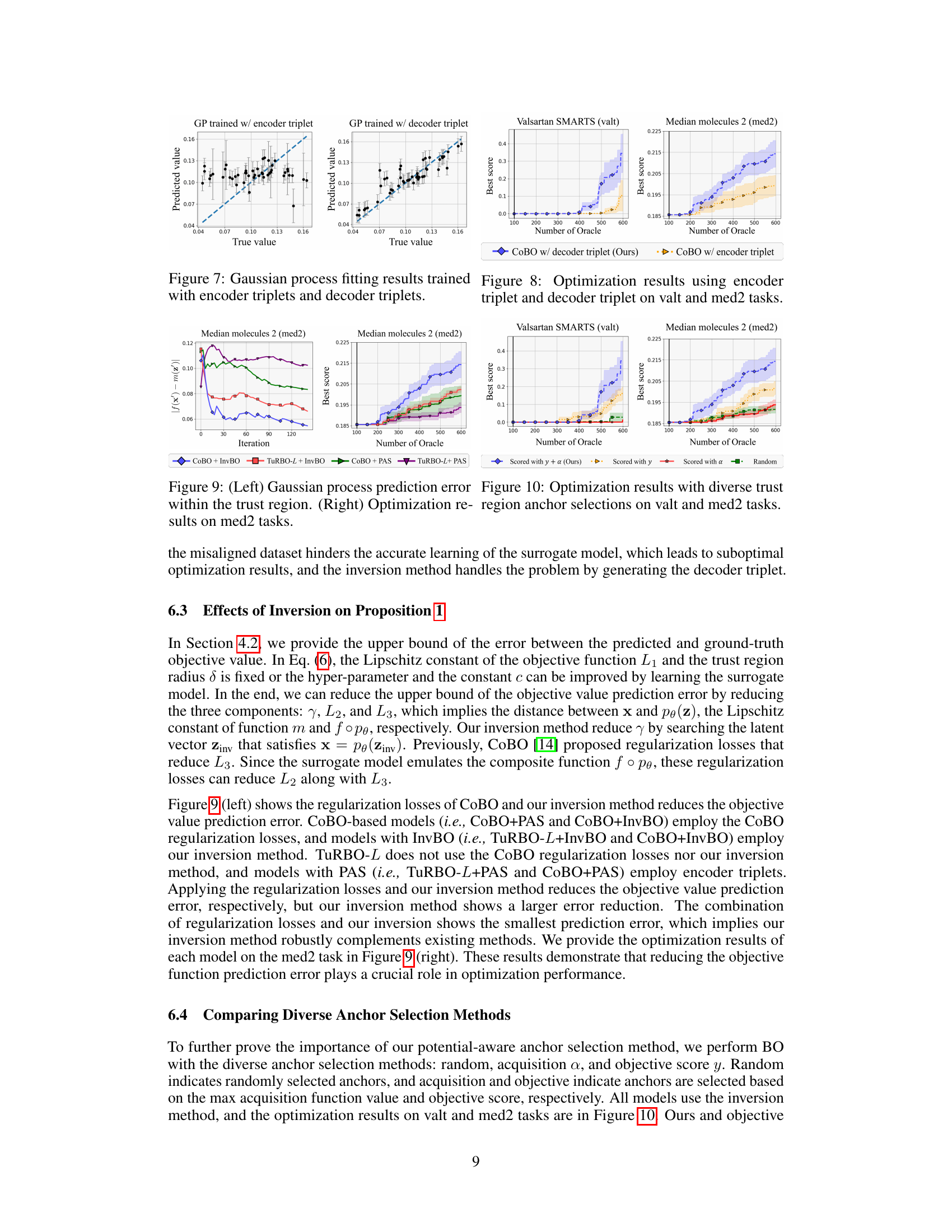
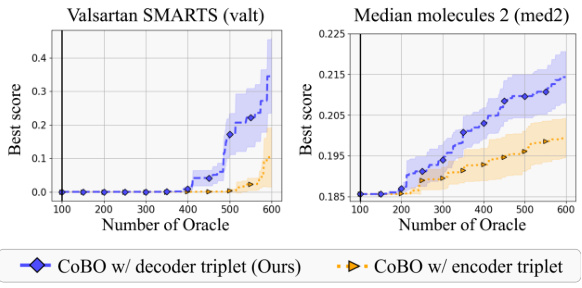
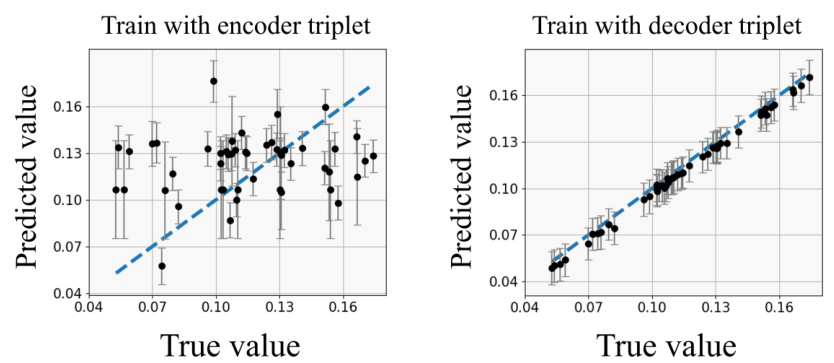
🔼 This figure illustrates the misalignment problem in Latent Bayesian Optimization (LBO). Due to the reconstruction error of the Variational Autoencoder (VAE), a single latent vector z can be mapped to two different input values (x and x’) resulting in two different objective function values (y and y’). This discrepancy makes it difficult to accurately learn a surrogate model of the objective function in the latent space, hindering the optimization process. The figure shows both the encoder and decoder triplets, highlighting the difference between the original input x and its reconstruction x'.
read the caption
Figure 1: Misalignment problem. In LBO, a latent vector z can be associated with two function values y and y' due to the reconstruction error of the VAE, i.e., x ≠ x'. (a) In Encoder triplet (x, z, y), latent vector z is associated with f(x), where x is the original input to the encoder, i.e., z = q(x). (b) In Decoder triplet (x', z, y'), z is associated with y' = f(x'), which is the objective function value of reconstructed input value x' using the decoder, i.e., x' = pθ(z). The discrepancy between y and y' hinders learning the accurate surrogate model g. We name this the ‘misalignment problem’.

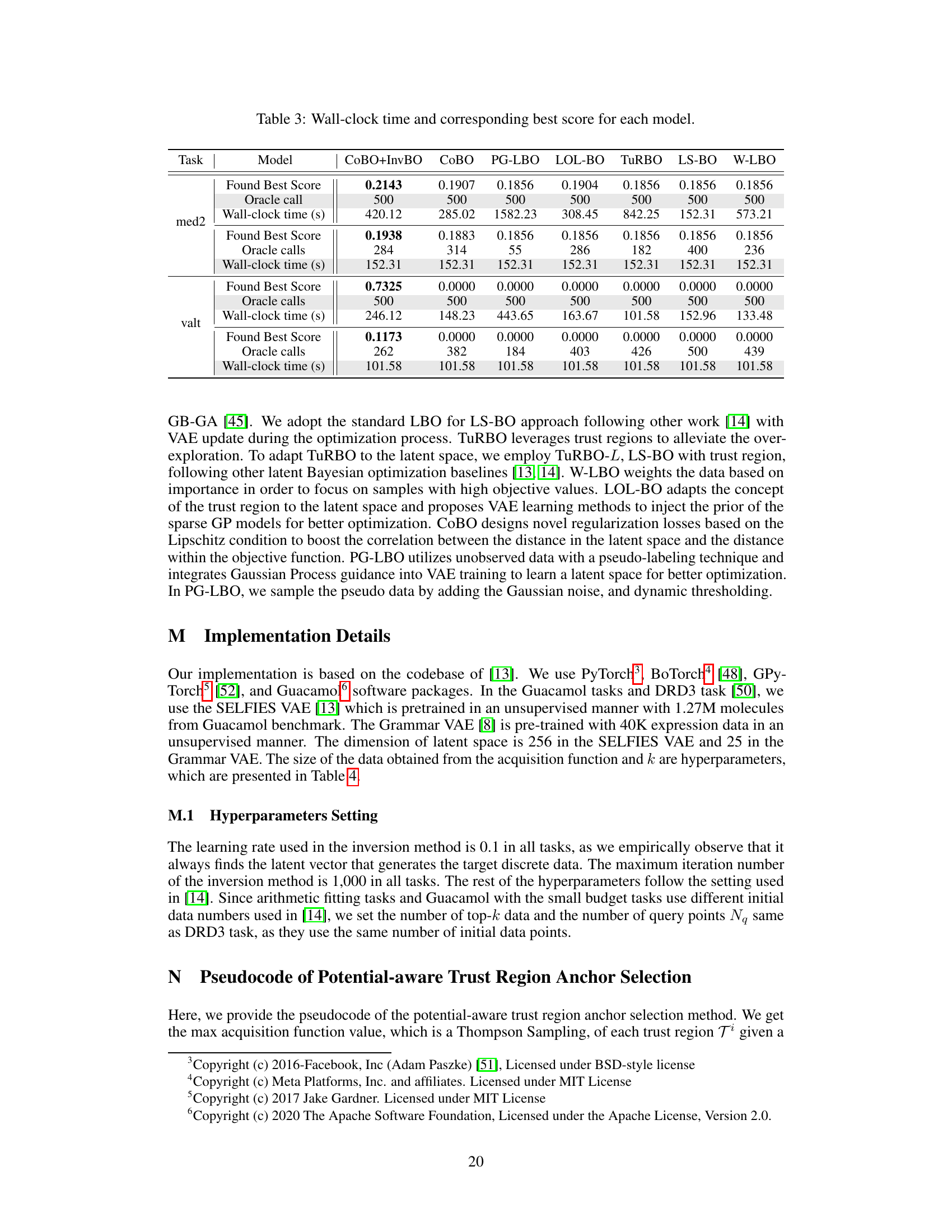
🔼 This table presents the optimization results of applying the proposed Inversion-based Latent Bayesian Optimization (InvBO) method to several trust-region based Latent Bayesian Optimization (LBO) methods on the Guacamol benchmark tasks. It shows the performance of different LBO methods (TURBO-L, LOL-BO, and COBO) with and without InvBO, across various numbers of oracle calls (100, 300, and 500). The results are presented as average scores, indicating the effectiveness of InvBO in improving the performance of existing LBO methods on these molecule design tasks.
read the caption
Table 1: Optimization results of applying InvBO to several trust region-based LBOs on Guacamol benchmark tasks. A higher score is a better one.

In-depth insights
#

Latent Space BO
#

Latent space Bayesian Optimization (BO) tackles the challenge of applying BO to high-dimensional or discrete input spaces by performing optimization in a continuous latent space. This approach leverages generative models, often Variational Autoencoders (VAEs), to map the complex input space to a lower-dimensional latent space where a simpler surrogate model can be effectively trained. The core idea is to learn a mapping between the latent space and the objective function, allowing for efficient exploration and exploitation of the objective landscape within the latent space. A crucial aspect is the decoder, which reconstructs inputs from the latent space. However, inaccuracies in this reconstruction, leading to a misalignment between the latent representation and the true objective function values, is a common problem. Addressing this misalignment is key to successful latent space BO, and techniques like inversion methods to find latent codes accurately representing original data points are crucial in enhancing performance. Effective anchor selection within trust region methods also plays a vital role in improving optimization, as the choice of anchor significantly impacts exploration within the latent space.

InvBO Method
#

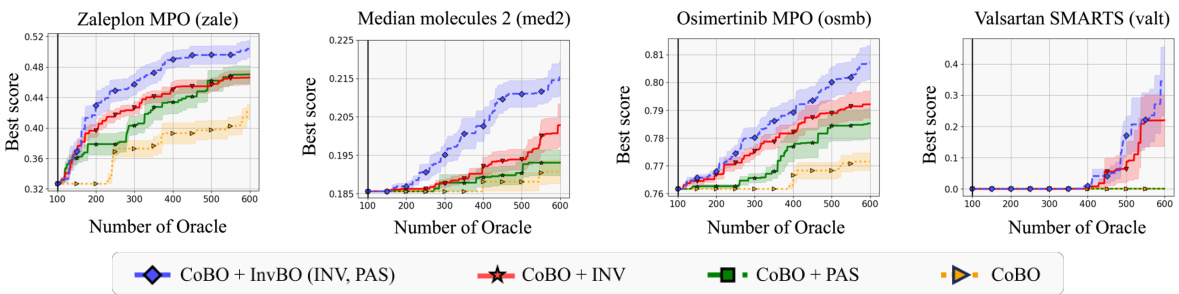
The InvBO method, a plug-and-play module designed to enhance Latent Bayesian Optimization (LBO), directly tackles the misalignment problem inherent in existing LBO approaches. This misalignment stems from reconstruction errors in the encoder-decoder architecture, hindering accurate surrogate model learning. InvBO ingeniously introduces an inversion method to find latent codes that perfectly reconstruct target data, thereby generating aligned triplets for training. This eliminates the need for additional, expensive oracle calls often required by alternative methods. Furthermore, InvBO incorporates potential-aware trust region anchor selection, moving beyond solely objective function value-based anchor choices. This improvement considers the trust region’s optimization potential, leading to more effective local searches. The combination of the inversion method and the potential-aware anchor selection results in significant performance gains across diverse real-world benchmarks, showcasing InvBO’s efficacy and general applicability as a powerful enhancement to the LBO framework.

Misalignment Fix
#

The concept of a “Misalignment Fix” in the context of Latent Bayesian Optimization (LBO) addresses a critical challenge arising from the reconstruction error inherent in encoder-decoder architectures. The core problem is that the latent space representation (the encoded version of the input data) may not perfectly reconstruct the original input data when decoded. This leads to a discrepancy, where multiple different inputs may map to the same latent point or vice versa. A successful misalignment fix must reconcile the discrepancies between the latent space and the original input space. This usually involves methods to ensure the generated latent codes accurately represent the original inputs, allowing for reliable surrogate model training and, ultimately, better optimization results. Several approaches are possible, including the development of more accurate encoder-decoder models, data augmentation techniques, or more advanced latent space exploration strategies. Effective misalignment fixes are crucial for the success of LBO, enabling its application in complex domains with high-dimensional or discrete input spaces.

Trust Region
#

Trust regions in optimization, particularly within the context of Bayesian Optimization (BO), serve as localized search spaces designed to enhance the efficiency and effectiveness of the search for optimal solutions. Instead of exploring the vast expanse of the entire input space, BO algorithms employing trust regions focus on smaller, carefully chosen areas surrounding promising candidate solutions. This technique helps mitigate the challenges of high-dimensionality and complex landscapes where a global search may be computationally prohibitive or inefficient. The size and location of the trust region are dynamically adjusted during the optimization process, expanding in promising regions and contracting in less fruitful areas. Effective trust region strategies are key to balancing exploration (searching new areas) and exploitation (refining existing candidates) within BO, resulting in faster convergence and higher-quality solutions. A crucial aspect of trust region methods is the selection of the anchor point — the center of the trust region. Strategic anchor point selection directly influences the algorithm’s ability to effectively navigate the local landscape. The success of trust region-based BO algorithms heavily relies on the interplay between the surrogate model’s accuracy in approximating the objective function within the trust region, and the algorithm’s capability to adapt the trust region’s size and position to leverage the information gathered during the optimization process.

InvBO Limits
#

InvBO, while demonstrating strong performance improvements, has limitations stemming from its reliance on a pre-trained VAE. The quality of the VAE’s generated samples directly influences InvBO’s effectiveness; a poorly performing VAE could hinder the optimization process. The inversion method, central to InvBO, assumes the decoder is perfectly capable of reconstructing inputs; deviations from this ideal introduce errors, limiting its accuracy. The potential-aware anchor selection, while improving exploration, might still struggle in highly complex or multimodal objective functions. Furthermore, the computational cost of inversion can increase the overall runtime, especially in high-dimensional latent spaces. Generalization to diverse tasks and datasets beyond the benchmarked ones requires further investigation. Therefore, future work should focus on addressing these limitations and enhancing robustness.

More visual insights
#

More on figures

🔼 This figure compares two methods for addressing the misalignment problem in Latent Bayesian Optimization (LBO). The misalignment problem arises because the reconstruction error of the Variational AutoEncoder (VAE) means one latent vector z can be associated with multiple objective function values. (a) shows the ‘recentering’ method, which generates a new input x’ from the latent vector z, evaluates f(x’), and uses (x’, z, f(x’)) as a training triplet. This requires additional function evaluations. (b) shows the proposed ‘inversion’ method, which finds a latent vector zinv that perfectly reconstructs a given input x, resulting in the aligned triplet (x, zinv, f(x)) without extra evaluations. The inversion method efficiently addresses the misalignment problem by leveraging the pre-trained decoder to directly find the corresponding latent code.
read the caption
Figure 2: Comparison of solutions to the misalignment problem. (a) Some works [13, 14] solve the misalignment problem by the recentering technique that generates the aligned triplet (x', z, y'). However, it requests additional oracle calls as y' = f(x') is unevaluated, and does not fully use the evaluated function value y = f(x). (b) The inversion method (ours) aims to find zinv that generates the evaluated data x to get the aligned triplet (x, zinv, y) without any additional oracle calls.

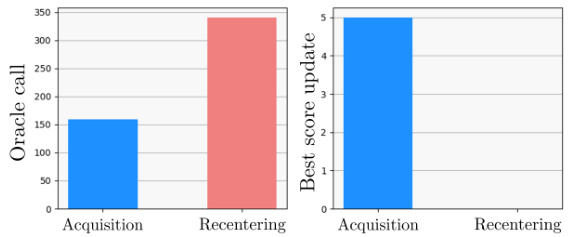
🔼 This figure compares two methods for solving the misalignment problem in Latent Bayesian Optimization: recentering and inversion. The left panel shows the number of oracle calls required for query selection using the acquisition function and for generating aligned triplets using the recentering technique. The recentering technique requires significantly more oracle calls. The right panel displays the number of objective function evaluations resulting in improved best scores for each approach. The inversion method (not shown in this figure) offers an advantage by not needing extra oracle calls to update the VAE.
read the caption
Figure 3: (Left) The number of oracle calls to evaluate the queries selected by the acquisition function (blue) and during the recentering (Red). (Right) The number of objective function evaluation that updates the best score.

🔼 This figure visualizes the performance comparison of different Bayesian Optimization methods on seven Guacamol benchmark tasks. The x-axis represents the number of oracle calls (the number of times the expensive black-box objective function is evaluated), while the y-axis shows the best objective function value achieved. Each line represents the average performance of ten independent runs for a particular method, and the shaded area indicates the standard error. The graph helps readers understand the relative effectiveness of each method in optimizing molecule design by showing which methods converge faster to better solutions given a limited evaluation budget.
read the caption
Figure 4: Optimization results on Guacamol benchmark tasks. The lines and ranges indicate the average and standard error of ten runs under the same settings. A higher score is a better score.

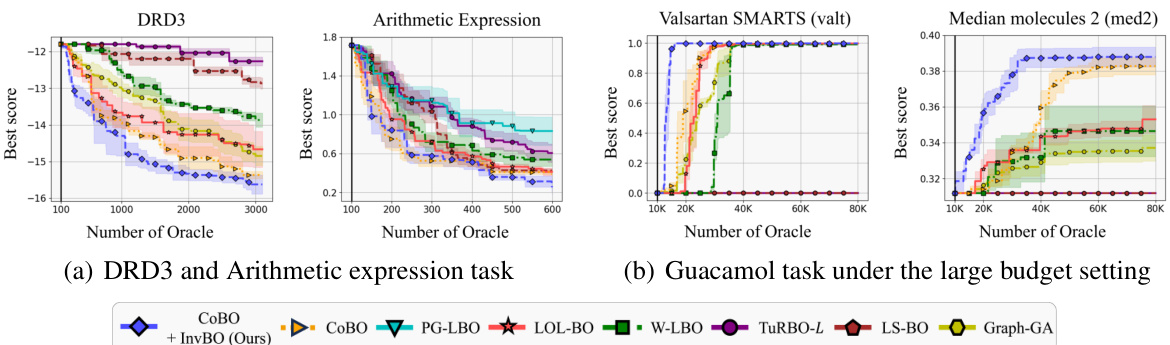
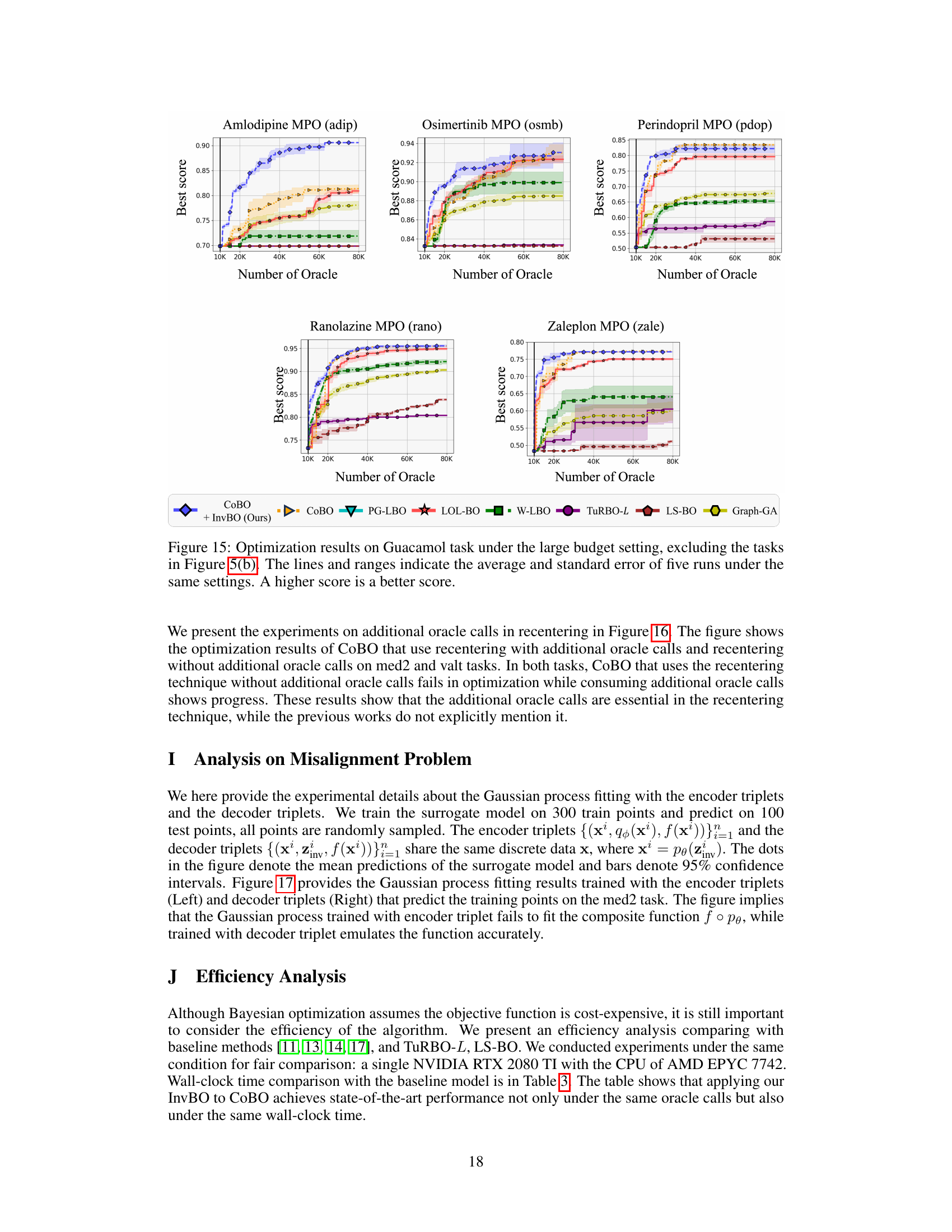
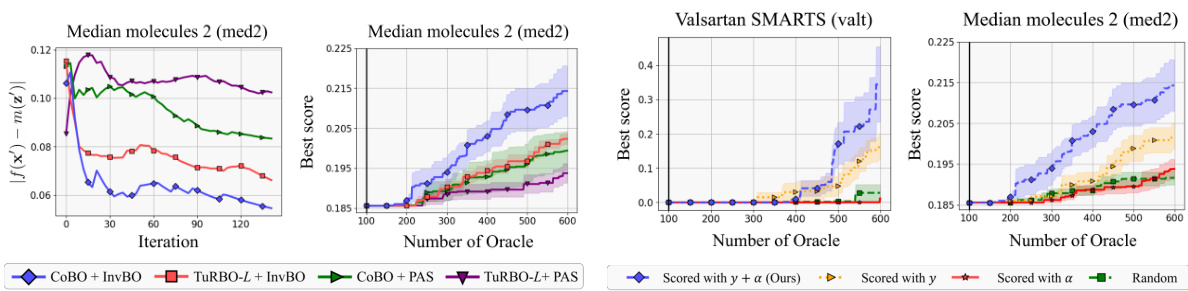
🔼 This figure presents the results of the proposed method InvBO against several baselines on three different tasks: DRD3, arithmetic expression, and Guacamol. The results are displayed for both small and large budget settings. In the DRD3 and arithmetic expression tasks, a lower score indicates better performance, while the Guacamol tasks use a higher score for better performance. The figure shows that InvBO consistently outperforms other LBO methods across all tasks and budget settings.
read the caption
Figure 5: Optimization results on various tasks and settings. Note that: (a) A lower score is a better score. (b) A higher score is a better score.

🔼 This figure compares two different approaches to handle the misalignment problem in Latent Bayesian Optimization (LBO). The misalignment problem arises from the reconstruction error of the variational autoencoder (VAE) used in LBO, where a single latent vector z can be associated with multiple different objective function values. (a) shows the ‘recentering’ technique used in previous LBO methods. This technique generates an aligned triplet (x’, z, y’) by finding a new input x’ that produces the same latent vector z and objective function value y. However, this requires additional evaluations of the objective function, making it inefficient. (b) presents the proposed ‘inversion’ method, which finds a latent vector zinv that perfectly reconstructs the original input x, forming an aligned triplet (x, zinv, y) without any extra function evaluations. The inversion method addresses the inefficiency of the recentering technique.
read the caption
Figure 2: Comparison of solutions to the misalignment problem. (a) Some works [13, 14] solve the misalignment problem by the recentering technique that generates the aligned triplet (x', z, y'). However, it requests additional oracle calls as y' = f(x') is unevaluated, and does not fully use the evaluated function value y = f(x). (b) The inversion method (ours) aims to find ziny that generates the evaluated data x to get the aligned triplet (x, Zinv, y) without any additional oracle calls.

🔼 This figure compares two approaches to address the misalignment problem in Latent Bayesian Optimization (LBO). The ‘Recentering’ method (a) generates an aligned triplet (x’, z, y’) by reconstructing the input x and evaluating the objective function f(x’) at the reconstructed point x’, but this requires additional function evaluations. In contrast, the proposed ‘Inversion’ method (b) finds the latent code ziny that perfectly reconstructs the original input x, resulting in an aligned triplet (x, zinv, y) without extra function evaluations. The inversion method leverages pre-trained decoder to avoid additional computational cost.
read the caption
Figure 2: Comparison of solutions to the misalignment problem. (a) Some works [13, 14] solve the misalignment problem by the recentering technique that generates the aligned triplet (x', z, y'). However, it requests additional oracle calls as y' = f(x') is unevaluated, and does not fully use the evaluated function value y = f(x). (b) The inversion method (ours) aims to find ziny that generates the evaluated data x to get the aligned triplet (x, Zinv, y) without any additional oracle calls.

🔼 This figure compares two methods for addressing the misalignment problem in Latent Bayesian Optimization (LBO). The recentering technique (a) generates aligned triplets by using the decoder to produce a reconstructed input, then evaluating it with the objective function. This requires extra function evaluations. In contrast, the proposed inversion method (b) finds the latent code that perfectly reconstructs the original input, requiring no extra function evaluations. The inversion method aims to directly generate an aligned triplet (x, z, y) using the pre-trained decoder.
read the caption
Figure 2: Comparison of solutions to the misalignment problem. (a) Some works [13, 14] solve the misalignment problem by the recentering technique that generates the aligned triplet (x', z, y'). However, it requests additional oracle calls as y' = f(x') is unevaluated, and does not fully use the evaluated function value y = f(x). (b) The inversion method (ours) aims to find ziny that generates the evaluated data x to get the aligned triplet (x, Zinv, y) without any additional oracle calls.

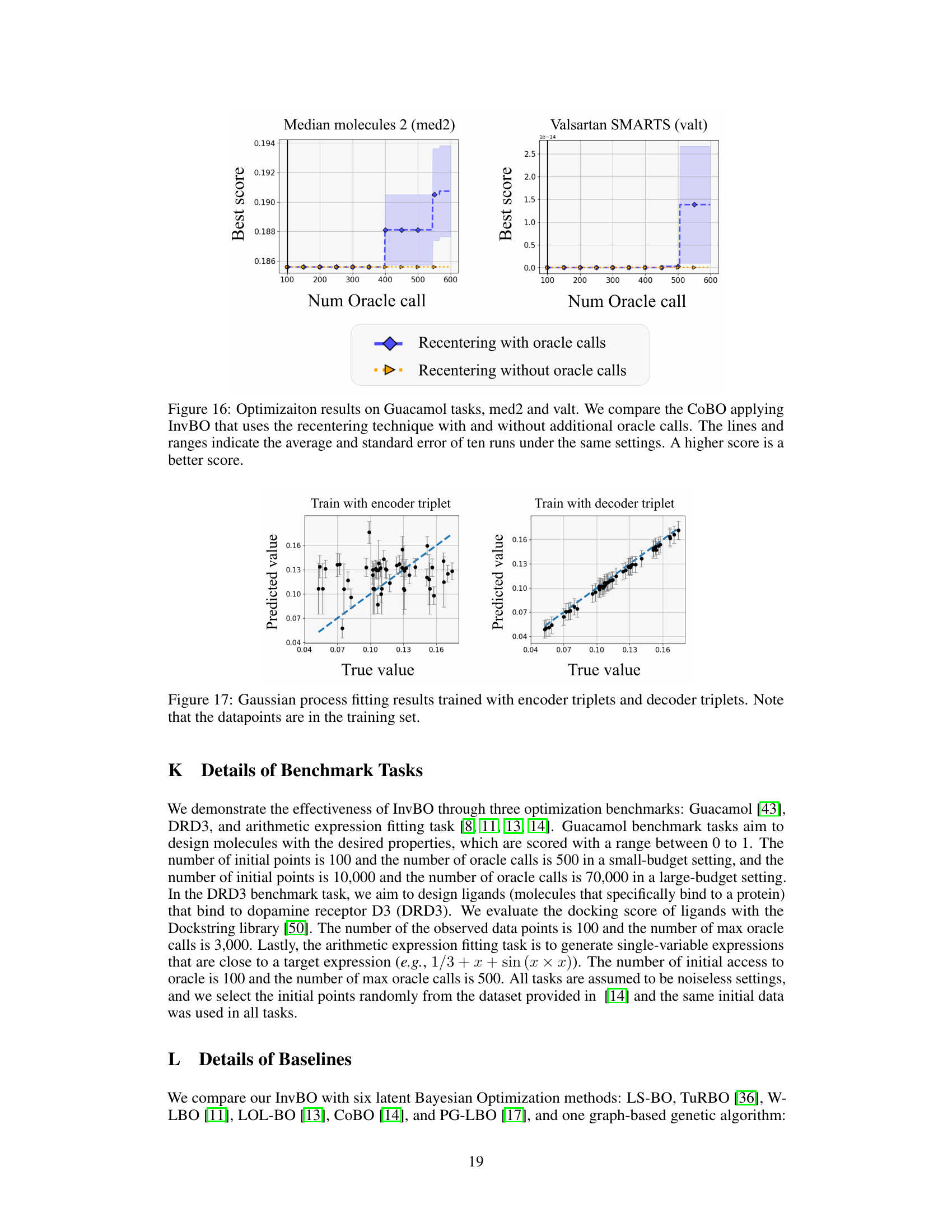
🔼 This figure empirically demonstrates the effectiveness of the inversion method by comparing the dissimilarity between the input data x and the reconstructed data po(z) with and without the inversion method. The inversion method aims to find a latent code z that perfectly reconstructs the input data x, thereby minimizing the dissimilarity between x and po(z). This figure shows that the inversion method consistently achieves zero dissimilarity, indicating that it generates perfectly aligned data. In contrast, the method without inversion results in significantly higher dissimilarity, indicating the generation of misaligned data. This visualization highlights the necessity of the inversion method for improving the accuracy of latent Bayesian optimization.
read the caption
Figure 12: Dissimilarity between x² and po (z²) with and without inversion on med2 and valt tasks. The measurement of dissimilarity is the normalized Levenshtein distance between the SELFIES token. (x-axis: number of iterations, y-axis: normalized Levenshtein distance.)

🔼 The figure shows the dissimilarity between the input data and the reconstructed data from the decoder with and without inversion method. The normalized Levenshtein distance is used as a measurement for the dissimilarity. The results demonstrate that using inversion method leads to better reconstruction (lower dissimilarity), while without inversion, the reconstruction is worse (higher dissimilarity).
read the caption
Figure 12: Dissimilarity between x² and po (z²) with and without inversion on med2 and valt tasks. The measurement of dissimilarity is the normalized Levenshtein distance between the SELFIES token. (x-axis: number of iterations, y-axis: normalized Levenshtein distance.)

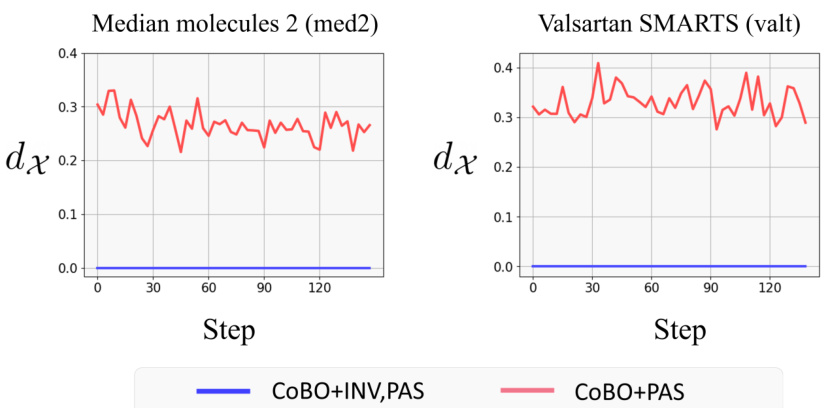
🔼 This figure compares the dissimilarity between the original input x and the reconstructed output pѳ(z) with and without using the inversion method proposed in the paper. The dissimilarity is measured using the normalized Levenshtein distance on SELFIES tokens. The results show that the inversion method effectively reduces the dissimilarity to near zero, indicating the generation of aligned data, while the method without inversion shows significantly higher dissimilarity, implying misaligned data.
read the caption
Figure 12: Dissimilarity between x² and pѳ(z²) with and without inversion on med2 and valt tasks. The measurement of dissimilarity is the normalized Levenshtein distance between the SELFIES token. (x-axis: number of iterations, y-axis: normalized Levenshtein distance.)

🔼 This figure compares the performance of the TuRBO algorithm with and without the potential-aware anchor selection (PAS) method on the 40-dimensional Ackley function. The results show the best score achieved over a series of iterations (number of oracle calls). Error bars represent the standard deviation across ten different runs, highlighting the algorithm’s robustness and performance consistency. The plot demonstrates that incorporating PAS into TuRBO improves optimization performance, achieving a better best score with fewer oracle calls.
read the caption
Figure 13: Optimization results of TuRBO and applying PAS to TuRBO on the synthetic Ackley function with 40 dimensions. The lines and ranges indicate the mean and a standard deviation of ten runs with different seeds.

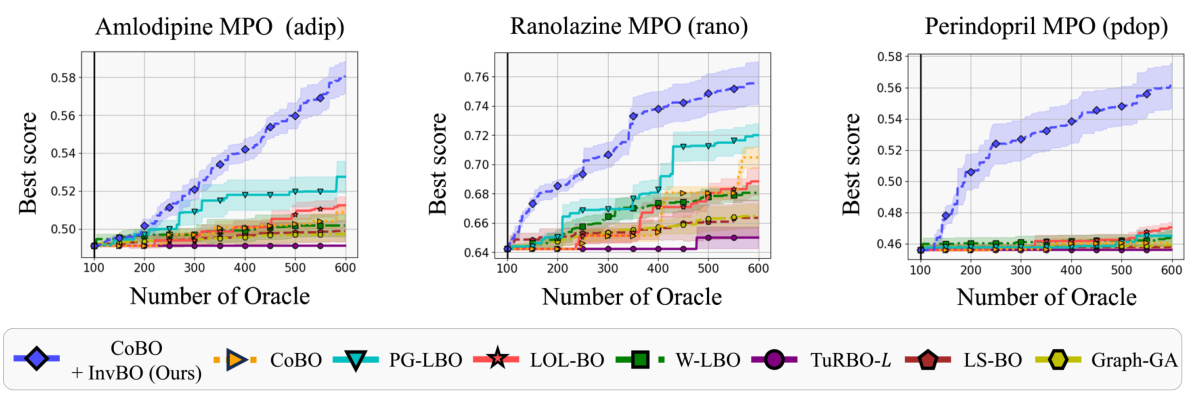
🔼 This figure presents the performance comparison of various Bayesian Optimization methods on seven Guacamol benchmark tasks. The x-axis represents the number of oracle calls (function evaluations), and the y-axis represents the best objective function score achieved. Each line represents the average performance across ten independent runs, with shaded areas showing the standard error. The figure illustrates how the proposed InvBO method improves the performance of different baseline methods (TURBO-L, LOL-BO, and CoBO) across various oracle call budgets, consistently achieving higher scores.
read the caption
Figure 4: Optimization results on Guacamol benchmark tasks. The lines and ranges indicate the average and standard error of ten runs under the same settings. A higher score is a better score.

🔼 This figure compares the performance of different Bayesian Optimization methods on seven Guacamol benchmark tasks, each with varying numbers of oracle calls (100, 300, and 500). The lines represent the average best score achieved by each method, while the shaded areas show the standard error across ten independent runs. The results illustrate the effectiveness of the proposed InvBO method in improving the performance of various LBO baselines. Higher scores indicate better results in terms of optimizing molecule properties.
read the caption
Figure 4: Optimization results on Guacamol benchmark tasks. The lines and ranges indicate the average and standard error of ten runs under the same settings. A higher score is a better score.

🔼 This figure compares two methods for addressing the misalignment problem in Latent Bayesian Optimization (LBO). The misalignment problem arises because the reconstruction error of the variational autoencoder (VAE) can lead to a single latent vector z being associated with multiple different function values. (a) shows the recentering technique, a prior approach that generates an aligned triplet by making additional oracle calls to obtain the function value for the reconstructed input. (b) illustrates the proposed inversion method, which directly finds a latent code that perfectly reconstructs the given input, thus generating an aligned triplet without extra oracle calls. The inversion method is more efficient, avoiding the need for additional function evaluations.
read the caption
Figure 2: Comparison of solutions to the misalignment problem. (a) Some works [13, 14] solve the misalignment problem by the recentering technique that generates the aligned triplet (x', z, y'). However, it requests additional oracle calls as y' = f(x') is unevaluated, and does not fully use the evaluated function value y = f(x). (b) The inversion method (ours) aims to find ziny that generates the evaluated data x to get the aligned triplet (x, Zinv, y) without any additional oracle calls.

🔼 This figure compares two methods for addressing the misalignment problem in Latent Bayesian Optimization (LBO). The ‘Recentering’ method (a) generates an aligned triplet by reconstructing the input data using the decoder and evaluating the objective function, but requires extra function evaluations. The proposed ‘Inversion’ method (b) efficiently finds the latent code that reconstructs the original data, avoiding extra function calls.
read the caption
Figure 2: Comparison of solutions to the misalignment problem. (a) Some works [13, 14] solve the misalignment problem by the recentering technique that generates the aligned triplet (x', z, y'). However, it requests additional oracle calls as y' = f(x') is unevaluated, and does not fully use the evaluated function value y = f(x). (b) The inversion method (ours) aims to find ziny that generates the evaluated data x to get the aligned triplet (x, Zinv, y) without any additional oracle calls.

TL;DR#

Key Takeaways#

Why does it matter?#

Visual Insights#

In-depth insights#

Latent Space BO#

InvBO Method#

Misalignment Fix#

Trust Region#

InvBO Limits#

More visual insights#

Full paper#