↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many researchers are interested in the capability of deep neural networks to learn effective representations despite being heavily overparameterized. This has sparked significant interest in the role of gradient methods and the noise they introduce during training on this capability. This paper studies this issue by analyzing the behavior of gradient methods on a simplified two-layer linear network. It focuses on the difference between GD and SGD, particularly how stochasticity affects the learning process.
The authors demonstrate that, unlike GD, SGD diminishes the rank of the network’s parameter matrix. Using continuous-time analysis, they derive a stochastic differential equation that explains this rank deficiency, highlighting a key regularization mechanism that results in simpler structures. Their findings are supported by experiments beyond the simplified linear network model, showing the phenomenon applies to more complex architectures and tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial because it reveals a fundamental difference in how stochastic gradient descent (SGD) and gradient descent (GD) impact the learning process in linear neural networks. It challenges existing assumptions about the role of noise in generalization by showing that noise, far from just helping the model to converge to better solutions, actively simplifies network structures by reducing rank. This research has important implications for understanding deep learning generalization and designing more efficient algorithms.
Visual Insights#
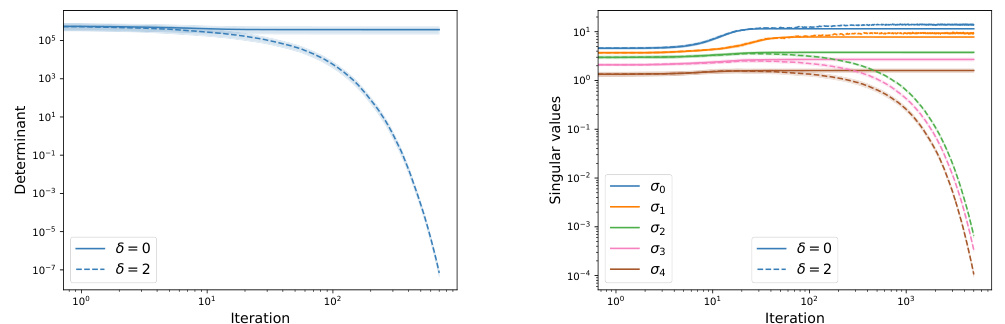
This figure shows the evolution of the model characteristics, specifically the determinant of matrix M and the top 5 singular values of matrix W1, under gradient flow (δ = 0) and stochastic gradient flow (δ = 2). The left panel illustrates how the determinant remains constant under gradient flow but decays to zero under stochastic gradient flow, highlighting a key difference between the two methods. The right panel displays the trajectories of the top 5 singular values. It shows how under stochasticity, the smaller singular values tend towards zero, indicating a rank deficiency that does not occur under gradient flow. This visualization supports the paper’s central claim about the impact of stochasticity on the rank of the parameter matrices.
Full paper#