TL;DR#
Adversarial training enhances machine learning model robustness against data manipulation. However, its theoretical understanding, especially in high-dimensional settings, remains limited. This paper focuses on high-dimensional linear regression, a fundamental model in machine learning, and investigates the statistical properties of adversarial training under l∞-perturbation (a common type of data perturbation). Prior work has primarily focused on asymptotic analysis, lacking non-asymptotic guarantees which are vital in practice.
This research provides a non-asymptotic analysis of adversarial training in linear regression. The authors demonstrate that under specific conditions (such as the restricted eigenvalue condition), the prediction error converges at the minimax rate, up to a logarithmic factor. They further extend their analysis to group adversarial training, showing that it can achieve even better results if the underlying data exhibits group sparsity. These theoretical findings offer valuable insights into the behavior of adversarial training in high-dimensional data and have significant implications for improving the robustness and efficiency of machine learning algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in high-dimensional statistics and machine learning. It provides rigorous theoretical guarantees for adversarial training in linear regression, a widely used but understudied technique. The results offer new insights into the statistical properties of adversarial training and could guide the development of more robust and efficient algorithms. Furthermore, the exploration of group adversarial training opens avenues for addressing the challenges posed by group-structured data, which is increasingly common in real-world applications. The minimax optimality results offer significant advancements for the field.
Visual Insights#
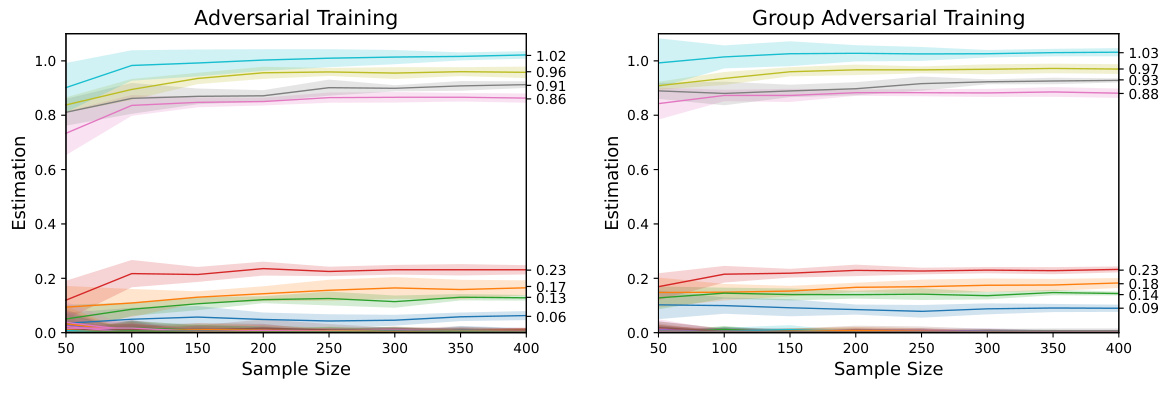
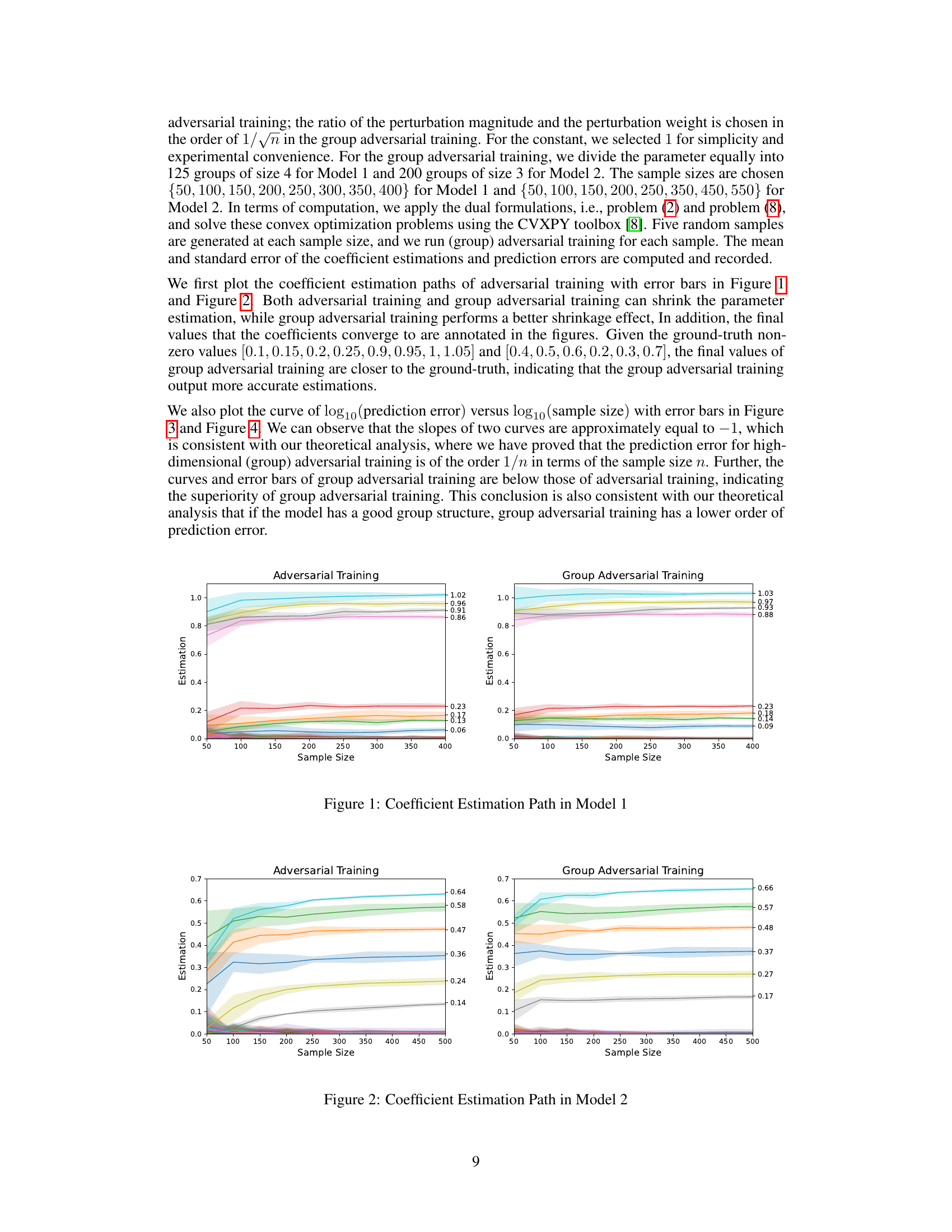
🔼 This figure shows the coefficient estimation paths for both adversarial training and group adversarial training in Model 1. Each colored line represents a different coefficient, and the shaded area around the line indicates the standard error of the mean. The x-axis shows the sample size, while the y-axis shows the estimated value of each coefficient. The figure demonstrates how the estimated values of the coefficients change with increasing sample size for both methods and visually compares the performance of the two approaches.
read the caption
Figure 1: Coefficient Estimation Path in Model 1
In-depth insights#
Adversarial Training#
Adversarial training is a crucial technique to enhance the robustness of machine learning models against adversarial attacks. Its core principle involves training the model not just on clean data, but also on adversarially perturbed data, crafted to intentionally mislead the model. This process forces the model to learn more robust and generalizable features, improving its ability to withstand malicious inputs. The effectiveness of adversarial training hinges on several factors, including the type of perturbation used (e.g., l∞, l2), the strength of the perturbation, and the choice of loss function. High-dimensional settings present unique challenges, requiring specialized techniques and theoretical analyses to guarantee convergence and minimax optimality. This paper focuses on these challenges and analyzes adversarial training in linear regression under high-dimensional and sparse assumptions, demonstrating the estimator’s ability to reach minimax optimality under l∞-perturbation. Furthermore, the study introduces group adversarial training which offers potential improvements when group structures within the input data are present. Overall, the research contributes to a deeper theoretical understanding of adversarial training, particularly in high-dimensional settings, offering insights into its statistical properties and demonstrating its practical benefits for creating more resilient machine learning models.
High-Dim Analysis#
A high-dimensional analysis in a research paper typically involves investigating statistical properties of data with a large number of variables (p) exceeding the number of observations (n), commonly known as the p » n setting. This presents unique challenges compared to traditional statistical methods. Key considerations include dealing with sparsity (assuming many variables have negligible effects), handling multicollinearity, and mitigating the curse of dimensionality. The choice of statistical methods is crucial. Regularization techniques like Lasso or Ridge regression are frequently employed to constrain model complexity and prevent overfitting. Theoretical guarantees are often pursued using tools such as concentration inequalities and restricted eigenvalue conditions. These provide insights into the convergence rates of estimators or prediction error and ensure statistical consistency even in high-dimensional spaces. High-dimensional analysis often explores the minimax optimality of estimators, showing that certain methods achieve the best possible rates of convergence. The analysis often involves intricate mathematical derivations and careful attention to probabilistic bounds. A critical aspect is validating the assumptions of the theoretical analysis through simulations or real-world data analysis.
Minimax Optimality#
The concept of “Minimax Optimality” in the context of high-dimensional adversarial training centers on determining whether an estimator (a method for approximating an unknown parameter) achieves the best possible performance in the worst-case scenario. The minimax rate represents the best achievable convergence rate for prediction error, given the inherent limitations posed by high dimensionality and adversarial perturbations. The paper investigates whether adversarial training, a technique aimed at improving robustness against attacks, can achieve this optimal rate. Establishing minimax optimality is crucial because it indicates that the estimator’s performance is not just good, but fundamentally optimal relative to a well-defined benchmark. The analysis likely involves deriving non-asymptotic bounds on the prediction error and showing that these bounds match the minimax rate, demonstrating the statistical efficiency of the approach. Such findings are significant as they offer strong theoretical guarantees, suggesting that adversarial training does not merely improve robustness, but also is statistically optimal under certain conditions. The work likely establishes sufficient conditions such as sparsity assumptions on the underlying parameter and certain conditions on the design matrix to guarantee minimax optimality. Understanding the precise conditions under which minimax optimality holds helps refine the design and application of adversarial training procedures.
Group Sparsity#
Group sparsity, in the context of high-dimensional data analysis, assumes that the relevant predictors cluster into groups, with all predictors within a group either being selected or not. This structure differs from standard sparsity, where individual predictors are selected independently. The key advantage of utilizing group sparsity is the increased efficiency and interpretability when dealing with correlated predictors. Since predictors often exhibit inherent relationships (e.g., genes in a pathway or features derived from the same source), modeling this structure can lead to improved performance and a more succinct model representation. Techniques leveraging group sparsity, such as the group lasso, provide a structured regularization that encourages the selection of entire groups of variables rather than individual ones. This results in improved prediction accuracy, especially when dealing with correlated predictors that exhibit strong group-wise effects. However, choosing appropriate group structures is crucial; incorrect grouping can hinder performance. Therefore, careful consideration of the underlying data relationships and appropriate selection of grouping methods are essential for successfully harnessing the benefits of group sparsity.
Future Research#
Future research directions stemming from this work on adversarial training in linear regression could explore several promising avenues. Extending the theoretical analysis beyond linear models to encompass generalized linear models or other non-linear settings is crucial for broader applicability. Investigating the impact of different perturbation norms beyond the l∞ norm and understanding their effect on model sparsity would provide valuable insights. A deeper investigation into the interplay between adversarial training and model selection techniques (like LASSO) is needed to optimize the balance between robustness and statistical efficiency. Furthermore, empirical studies comparing different adversarial training strategies across diverse datasets and tasks would strengthen the findings and provide practical guidance. Finally, developing more efficient algorithms for high-dimensional adversarial training is vital, as current approaches can be computationally demanding. Addressing these areas would significantly advance our understanding of adversarial training and pave the way for building more robust and reliable machine learning models in real-world applications.
More visual insights#
More on figures

🔼 This figure displays the coefficient estimation paths for both adversarial training and group adversarial training in Model 2. The x-axis represents the sample size, and the y-axis shows the estimated coefficient values. Multiple lines represent the estimations from five separate runs for each sample size. The shaded regions around the lines indicate the standard error. The figure shows how the estimated coefficients converge towards the ground truth values as the sample size increases, illustrating the effectiveness of both methods. The legend provides the ground truth values for comparison. This plot specifically compares the two different methods in the context of model 2.
read the caption
Figure 2: Coefficient Estimation Path in Model 2

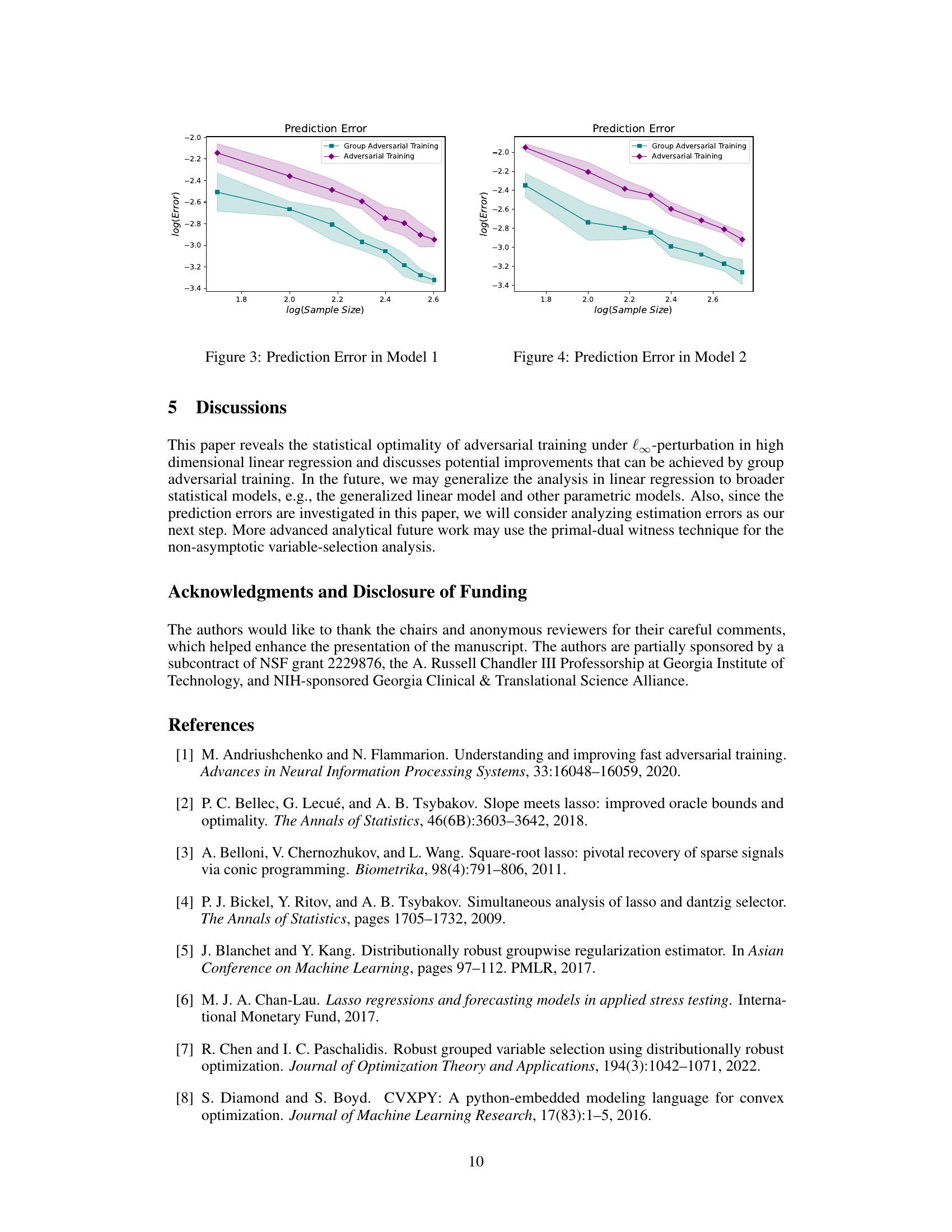
🔼 This figure shows the prediction error in Model 1 for both adversarial training and group adversarial training. The x-axis represents the logarithm of the sample size, while the y-axis represents the logarithm of the prediction error. The shaded area represents the standard error of the mean. We can observe that the prediction error decreases as the sample size increases. Additionally, group adversarial training has a lower prediction error compared to adversarial training.
read the caption
Figure 3: Prediction Error in Model 1

🔼 The figure shows the prediction error of both adversarial training and group adversarial training in Model 1 with different sample sizes. The prediction error is presented as log10(prediction error) versus log10(sample size). Error bars are included to show variability. The results suggest that group adversarial training leads to lower prediction error compared to adversarial training.
read the caption
Figure 3: Prediction Error in Model 1
Full paper#