↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Recurrent reinforcement learning (RL) shows promise for handling partially observable environments (POMDPs), but existing methods suffer from training instability. This is largely due to the autoregressive nature of recurrent neural networks (RNNs), causing small parameter changes to lead to large output variations, particularly over long sequences. This instability affects the learning process, potentially leading to poor performance.
To address this, the paper introduces RESEL (Recurrent Off-policy RL with Context-Encoder-Specific Learning Rate), a novel algorithm that uses a lower learning rate for the RNN context encoder than for other layers. This strategy stabilizes training while maintaining efficiency. Extensive experiments on 18 POMDP and 5 MDP tasks demonstrate that RESEL significantly improves training stability and achieves superior performance compared to previous recurrent RL methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the instability issue in recurrent off-policy reinforcement learning, a significant hurdle in applying RL to real-world partially observable environments. By introducing RESEL and demonstrating its effectiveness across various tasks, the authors provide a practical solution and pave the way for more stable and efficient RL algorithms. This work is especially important for researchers working on real-world applications of RL where partial observability is common, like robotics and autonomous driving.
Visual Insights#
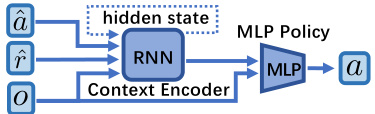
This figure shows a recurrent policy architecture commonly used in reinforcement learning. It consists of a recurrent neural network (RNN)-based context encoder, which processes the current observation, the last action, and the reward to extract unobservable hidden states. An MLP policy then uses these hidden states along with the current observation to generate actions. The architecture is designed to handle partially observable Markov decision processes (POMDPs), where the full state of the environment is not directly observable.

This table compares the average performance of different reinforcement learning algorithms on five classic MuJoCo locomotion tasks. The algorithms compared are TD3, SAC, TQC, TD3+OFE, TD7, and the proposed RESEL algorithm. The performance is measured at 5 million time steps and reported as the average return ± standard error over six independent trials. The table highlights RESEL’s competitive performance against state-of-the-art methods.
In-depth insights#
RESeL Algorithm#
The RESeL algorithm tackles the instability issues in recurrent off-policy reinforcement learning by introducing a context-encoder-specific learning rate. This addresses the problem of amplified output variations in RNNs caused by autoregressive nature, where even small parameter changes lead to large output differences over long sequences. RESeL uses a lower learning rate for the RNN context encoder than for other MLP layers, enhancing stability without sacrificing training efficiency. This technique is integrated into existing off-policy RL methods (e.g., SAC), improving performance and stability across various POMDP tasks and MDP locomotion tasks. The core innovation lies in the differentiated learning rate approach, which is supported by theoretical analysis showcasing the amplification of output variations in RNNs. Experiments show that RESeL significantly improves the training stability and achieves competitive or superior performance to state-of-the-art methods.
RNN Instability#
Recurrent Neural Networks (RNNs), while powerful for sequential data processing, are notorious for training instability. This instability primarily stems from the autoregressive nature of RNNs, where small parameter changes at the beginning of a sequence are amplified exponentially as the sequence unfolds. This phenomenon is particularly problematic in reinforcement learning (RL), where long temporal dependencies are common, leading to difficulties in stable Q-function training. The autoregressive property causes even slight parameter adjustments to result in significant output variations over long trajectories, leading to inconsistent and unreliable learning updates. The instability is further exacerbated in off-policy RL algorithms due to the bootstrapping of Q-values, making the training process highly sensitive to these variations. Therefore, addressing RNN instability in RL demands careful consideration of learning rate scheduling, alternative architectures, and regularization strategies to mitigate the effects of error propagation and enhance training stability. Techniques like using a lower learning rate specifically for the RNN context encoder, gradient clipping, and ensemble methods have been shown to improve stability, but further research is required to develop more robust training methods for RNNs in RL.
Learning Rate Impact#
The concept of ‘Learning Rate Impact’ in the context of a research paper likely centers on how the learning rate, a crucial hyperparameter in training machine learning models, affects the model’s performance, stability, and convergence. A thoughtful analysis would explore the interplay between learning rate and model architecture, particularly focusing on the impact on recurrent neural networks (RNNs) which are known for their susceptibility to instability during training. The discussion might delve into how different learning rates for various components of the model (e.g., context encoder versus other layers) impact the training dynamics, focusing on the trade-offs between training speed and stability. This would also include an exploration of phenomena like gradient explosion or vanishing gradients which are amplified in RNNs trained with unsuitable learning rates, leading to training instability. The analysis should also include empirical evidence of the impact of various learning rate schedules, comparing the model’s performance (e.g., convergence speed, final accuracy) across different learning rate settings. Finally, a discussion of the optimal learning rate selection strategies is essential, including any proposed methodologies or insights for determining effective learning rate schedules adapted to the specific properties of RNNs, such as context-encoder-specific learning rates.
POMDP Experiments#
A hypothetical ‘POMDP Experiments’ section would detail the empirical evaluation of a proposed reinforcement learning (RL) algorithm on various partially observable Markov decision process (POMDP) tasks. This would involve a rigorous comparison against established baselines, demonstrating improvements in performance metrics such as average return, success rate, or training stability. The choice of POMDP environments would be crucial, showcasing the algorithm’s ability to handle diverse challenges in partial observability, including classic POMDP problems, meta-learning scenarios, and credit assignment tasks. A comprehensive experimental setup would involve hyperparameter tuning, multiple random seeds for each experiment to ensure statistical significance, and clear visualizations of learning curves. Ablation studies would isolate the impact of key design choices, confirming their contribution to the algorithm’s effectiveness. The results section should critically analyze the findings, discussing any unexpected outcomes and highlighting the algorithm’s strengths and limitations in the context of POMDP settings. Detailed analyses of these experiments, possibly including statistical tests, would be important to confirm the validity and significance of the findings.
Future Work#
The “Future Work” section of this research paper would ideally explore several avenues. Extending RESEL to more complex environments is crucial; real-world applications often present greater challenges than the simulated POMDPs and MDPs used in this study. Further, investigating the optimal learning rate strategy deserves attention. While the paper demonstrates the effectiveness of a context-encoder-specific learning rate, a more adaptive or automated method for determining optimal rates across various tasks and environments would greatly enhance the algorithm’s usability. Additionally, a deeper theoretical analysis of the amplification factor is needed to further solidify the understanding of RNN instability in RL and potentially lead to more robust solutions beyond just learning rate adjustments. Finally, exploring the algorithm’s scalability to larger and higher-dimensional state spaces would be important for practical applications. The paper’s current experiments could be expanded to test the algorithm’s limits and identify potential bottlenecks. The results may inform the design of more efficient architectures and training strategies.
More visual insights#
More on figures
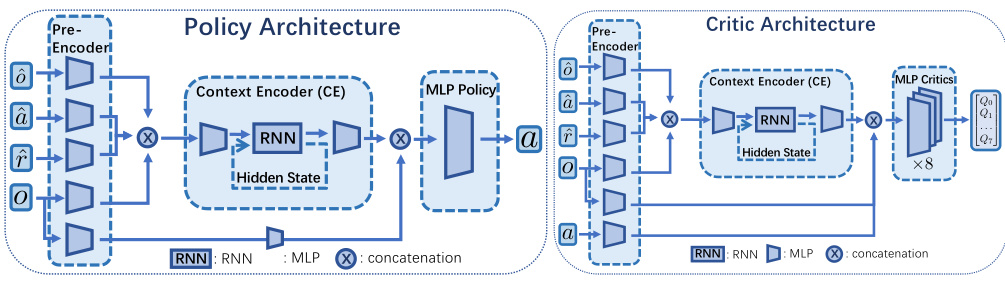
The figure shows the architectures of both policy and critic networks in the RESEL model. Both networks share a similar structure, beginning with pre-encoders that process observations, actions, and rewards, followed by a context encoder using an RNN (like GRU or Mamba) to extract hidden states. The output of the context encoder is then fed to an MLP policy (for the policy network) or multiple MLP critics (for the critic network). The use of multiple critics implements the ensemble-Q mechanism from REDQ for improved stability.
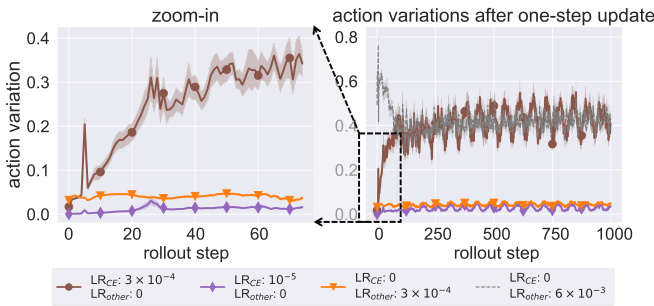
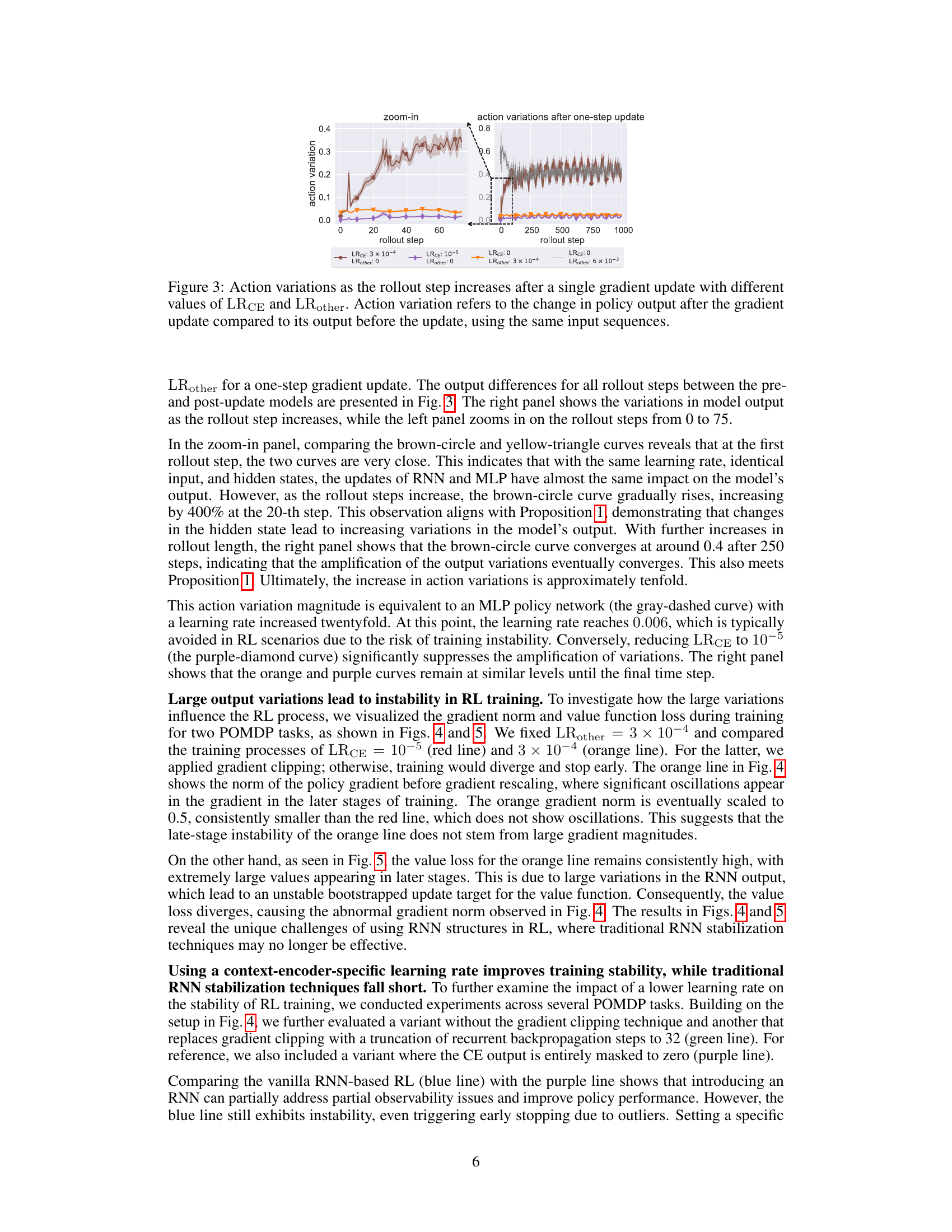
The figure shows how action variations change over rollout steps after a single gradient update. It compares different learning rates for the context encoder (LRCE) and other layers (LRother). The left panel zooms in on the initial steps, highlighting how small initial changes are amplified over time with the autoregressive nature of RNNs when LRCE is high. The right panel shows the overall trends, demonstrating that using a lower LRCE for the context encoder stabilizes training, preventing the large output variations that occur when a higher LRCE is applied.
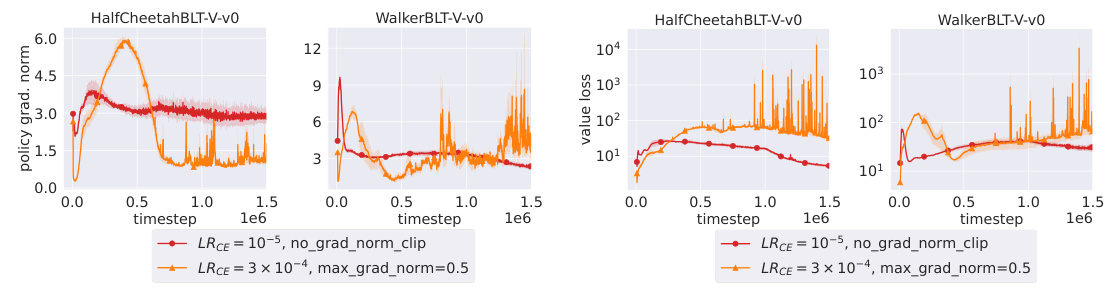
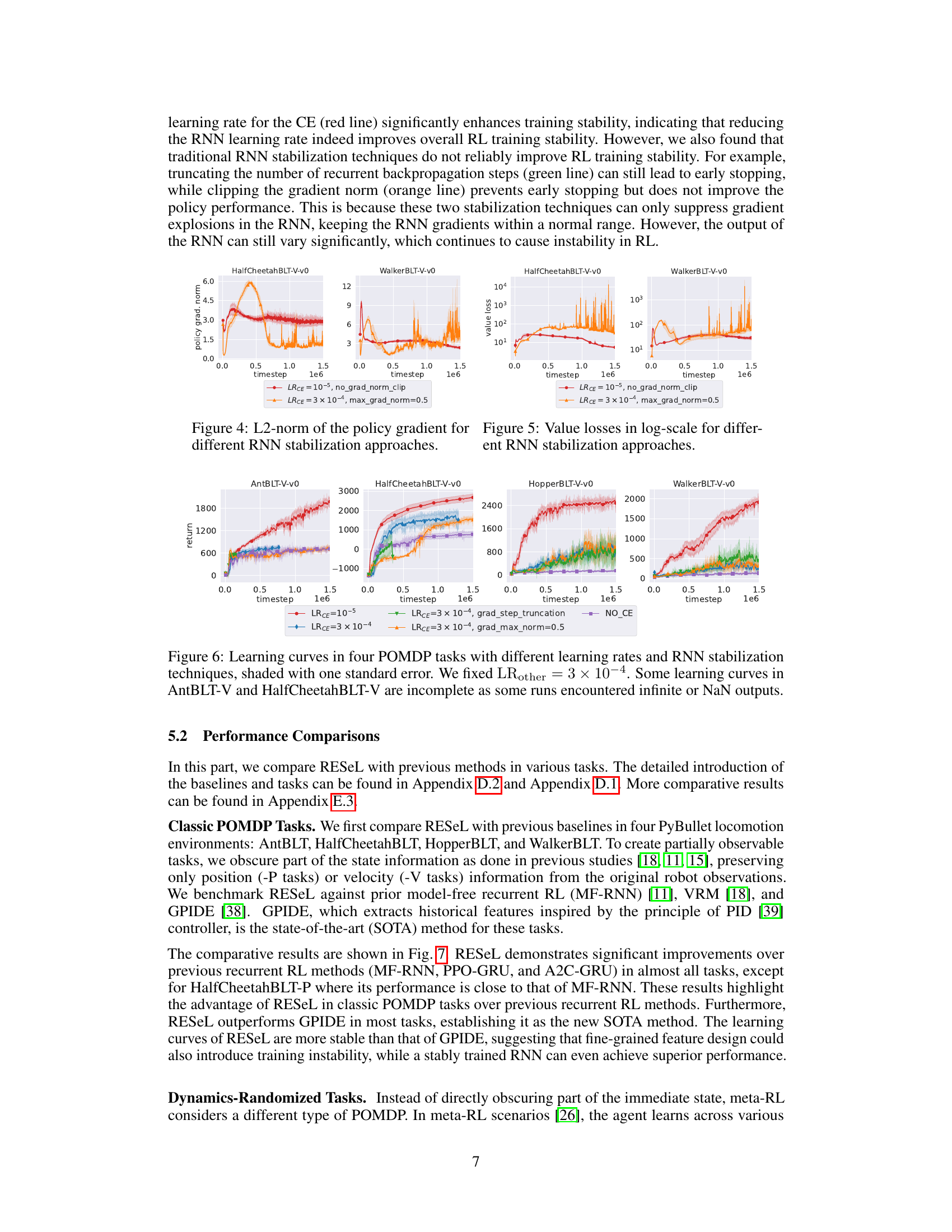
This figure visualizes the L2-norm of the policy gradient during training for two POMDP tasks (HalfCheetahBLT-V-v0 and WalkerBLT-V-v0). It compares two different learning rate settings for the context encoder (LRCE): LRCE = 10⁻⁵ (red line) and LRCE = 3 × 10⁻⁴ (orange line). The orange line uses gradient clipping to prevent divergence, which highlights the instability introduced by the higher learning rate. The y-axis represents the L2-norm of the policy gradient, and the x-axis represents the training timestep. The plots show that the lower learning rate (red line) leads to significantly more stable training with much less oscillation in the gradient norm compared to the higher learning rate (orange line) which shows large oscillations and ultimately leads to clipping.
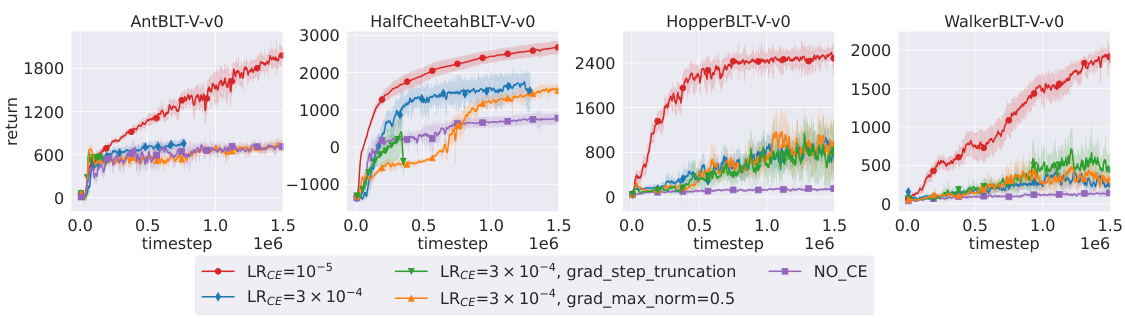
This figure compares the performance of Recurrent Off-policy RL with Context-Encoder-Specific Learning Rate (RESEL) with different learning rates for the context encoder (RNN) and other layers (MLP). It displays learning curves on four POMDP tasks, showing return over time. The shaded area represents one standard error. The results highlight the impact of a lower learning rate for the context encoder in stabilizing training and improving performance, especially when compared to the case with the same learning rates for both context encoder and other layers.
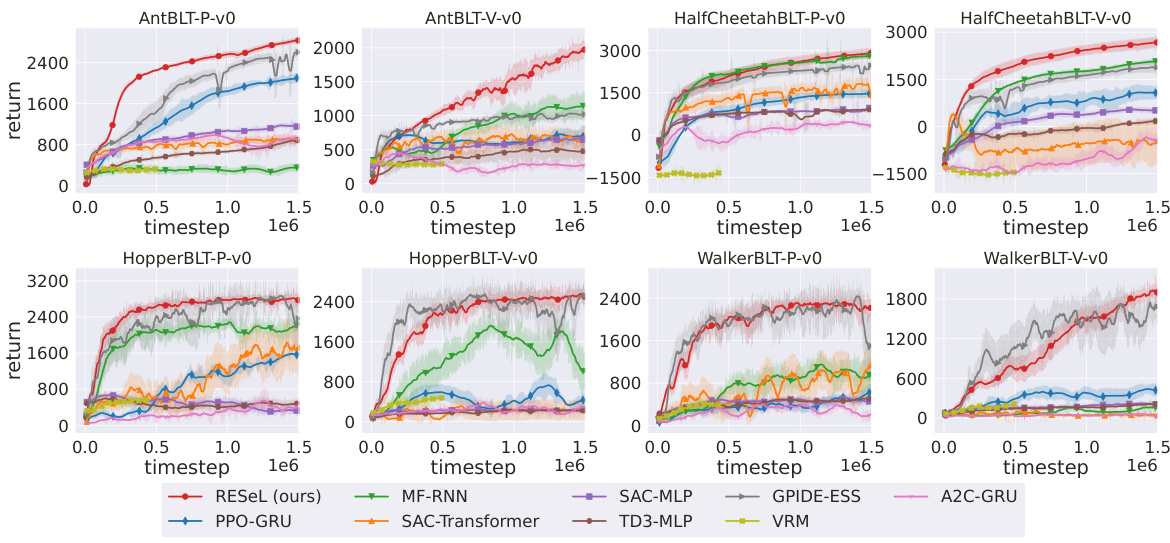
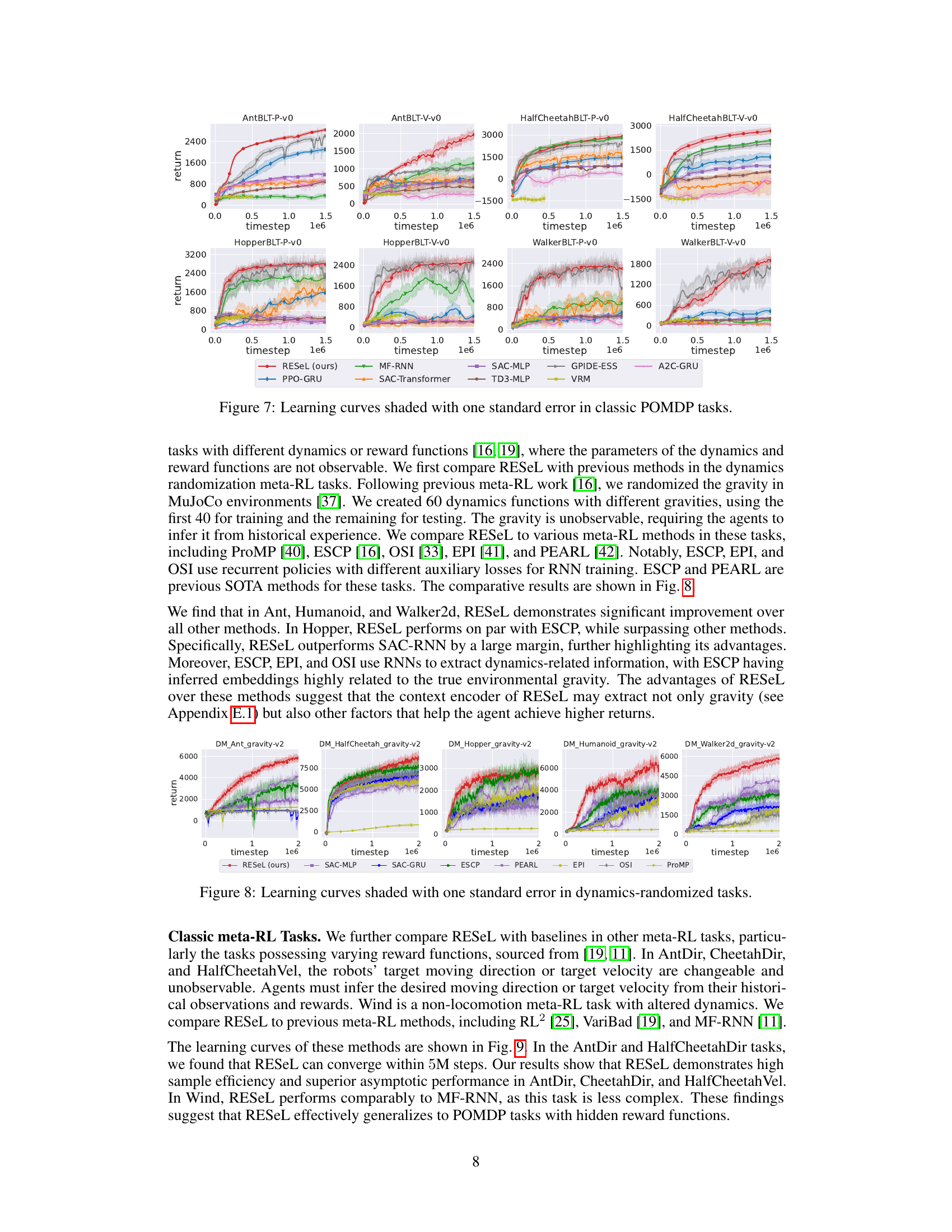
This figure displays the learning curves for several recurrent reinforcement learning algorithms across four classic partially observable Markov decision process (POMDP) tasks. The tasks involve robotic locomotion (Ant, HalfCheetah, Hopper, and Walker) with partial observability induced by obscuring either velocity or position information. The algorithms compared include RESEL (the proposed method), MF-RNN, SAC-MLP, PPO-GRU, A2C-GRU, TD3-MLP, VRM, and GPIDE-ESS (state-of-the-art). The curves show the cumulative reward obtained over time, illustrating the training stability and performance of each algorithm. Shading represents one standard error.
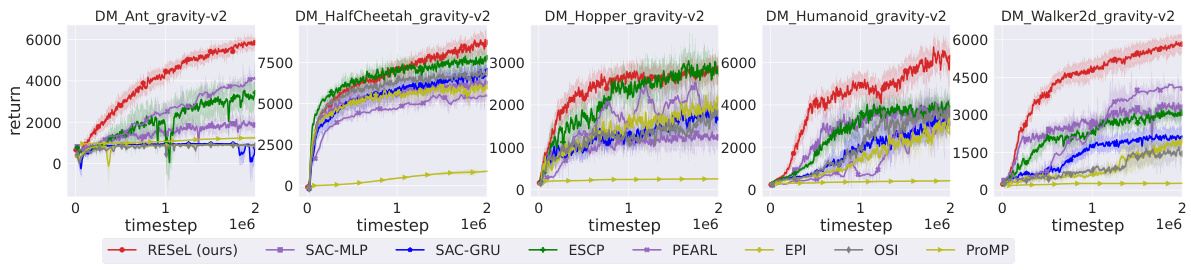
This figure presents the learning curves for five different MuJoCo locomotion tasks (Ant, HalfCheetah, Hopper, Humanoid, and Walker2d) under dynamics randomization. The x-axis represents the training timesteps, and the y-axis represents the average return. Multiple lines are shown for each task, representing different reinforcement learning algorithms being compared: RESEL (the proposed method), SAC-MLP, SAC-GRU, ESCP, PEARL, EPI, OSI, and ProMP. The shaded area around each line indicates the standard error over multiple runs. The purpose is to show the comparative performance of RESEL against existing state-of-the-art meta-RL algorithms in scenarios where the environment dynamics are partially observable (gravity is randomized and thus not directly available to the agent).
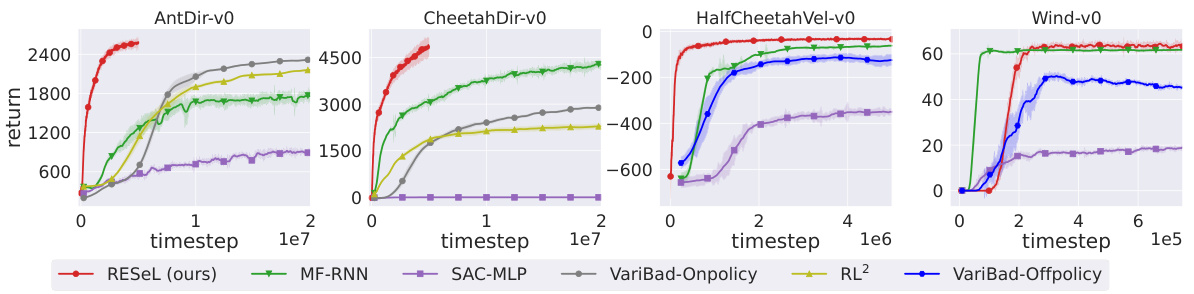
This figure presents the learning curves for four different meta-RL tasks: AntDir-v0, CheetahDir-v0, HalfCheetahVel-v0, and Wind-v0. Each curve represents the performance of a different algorithm over time, showing the average return achieved by each algorithm. The shaded regions represent the standard error around the mean return. The algorithms compared are RESeL (the proposed method), MF-RNN, SAC-MLP, VariBad-Onpolicy, RL2, and VariBad-Offpolicy. The figure demonstrates the relative performance of each algorithm on these challenging meta-RL tasks, highlighting the strengths and weaknesses of each approach in terms of learning speed, stability, and final performance.
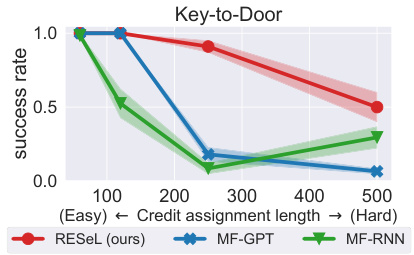
This figure shows the success rate of three different algorithms (RESEL, MF-GPT, and MF-RNN) on the Key-to-Door task with varying credit assignment lengths. The x-axis represents the credit assignment length, ranging from 60 to 500. The y-axis represents the success rate, ranging from 0 to 1. The results indicate that RESeL achieves comparable or better success rates than MF-GPT and MF-RNN across all credit assignment lengths, showing its robustness in handling the task complexity.
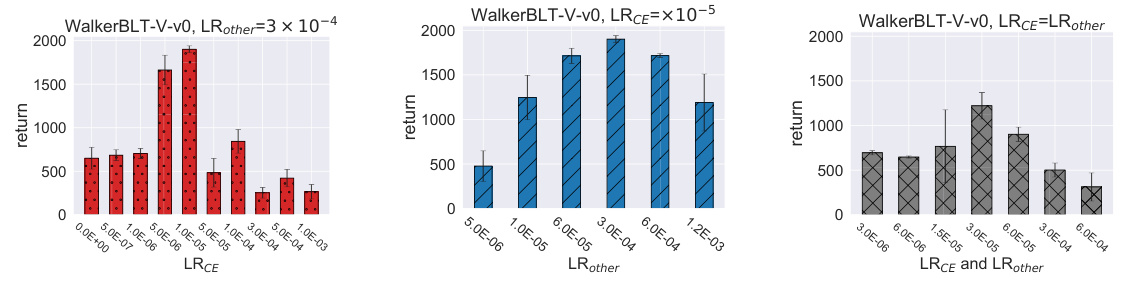
This figure presents the results of sensitivity studies conducted to determine the optimal learning rates for the context encoder (LRCE) and other layers (LRother) in the RESEL algorithm. The plots show how the average final return of the WalkerBLT-V-v0 task varies with different values of LRCE (while LRother is fixed), LRother (while LRCE is fixed), and when LRCE and LRother are set to the same value. The results highlight the importance of using distinct learning rates for the context encoder and other layers in order to achieve optimal performance and training stability.
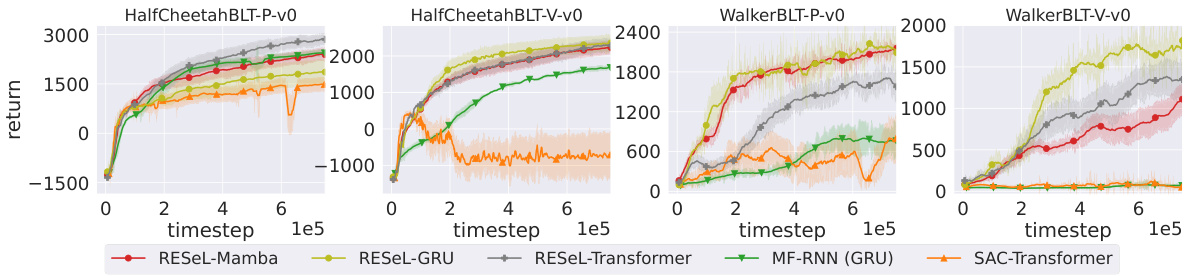
This figure compares the learning curves of the exploration policy (with exploration noise added to actions) across different RNN architectures: RESEL-Mamba, RESEL-GRU, RESEL-Transformer, MF-RNN (GRU), and SAC-Transformer. The results show the stochastic policy performance over time (timesteps) across four partially observable locomotion tasks. The plot helps visualize the effect of the chosen recurrent neural network (RNN) architecture on the stability and performance of the reinforcement learning agent. While the caption is short, the figure’s purpose is to show the effectiveness of RESEL in various RNN settings and compare it against prior state-of-the-art methods.
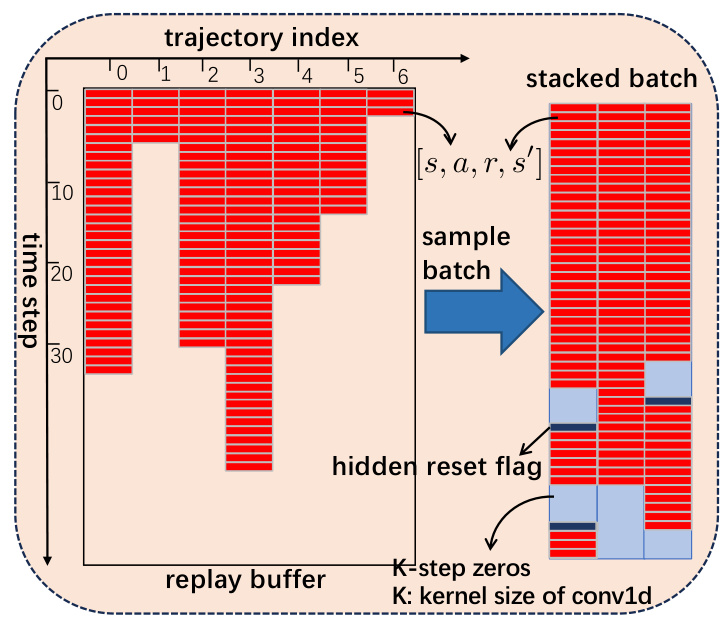
This figure illustrates how to sample a stacked batch from a replay buffer in RESEL, an algorithm designed to handle varying trajectory lengths in reinforcement learning. Because the lengths of trajectories in the replay buffer are not uniform, a simple concatenation wouldn’t work. Instead, the algorithm stacks shorter trajectories along the time dimension, using a hidden reset flag at the beginning of each trajectory to reset the RNN’s hidden state and preventing mixing between trajectories. To prevent convolution from mixing trajectories, K-steps of zero data are inserted between trajectories.
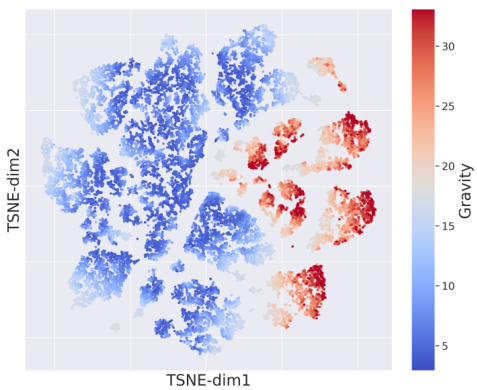
This figure shows a t-SNE visualization of the context encoder’s outputs in the HalfCheetah environment with varying gravity. The colorbar indicates the magnitude of the gravity acceleration. The x and y axes represent the 2D t-SNE embedding. The visualization demonstrates that the context encoder’s outputs are not randomly distributed but rather cluster according to the gravity acceleration. This suggests that RESEL successfully learns to extract gravity-related information from the environment’s dynamics.
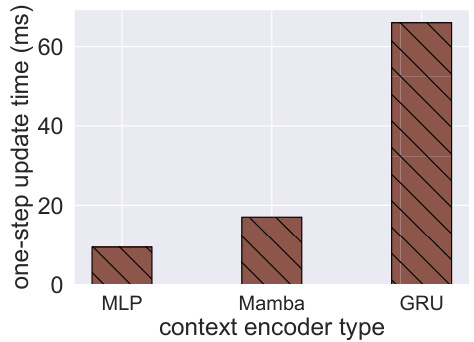
This figure shows the one-step update time cost comparison between three different context encoder types: MLP, Mamba, and GRU. The results demonstrate that Mamba significantly reduces the update time compared to GRU, while still achieving faster speeds than MLP.
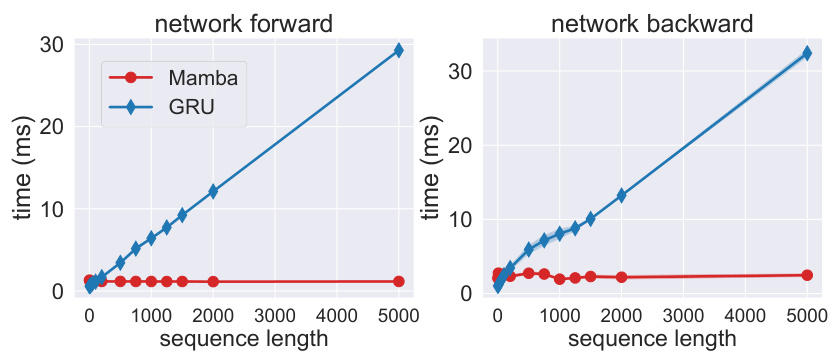
This figure compares the time overhead of GRU and Mamba layers during network forward and backward passes with varying sequence lengths. The left panel shows the forward pass time, while the right panel depicts the backward pass time. The plot illustrates that the time cost for GRU increases linearly with the sequence length, while the time cost for Mamba remains relatively constant, demonstrating better scalability and efficiency for Mamba, especially when dealing with longer sequences.
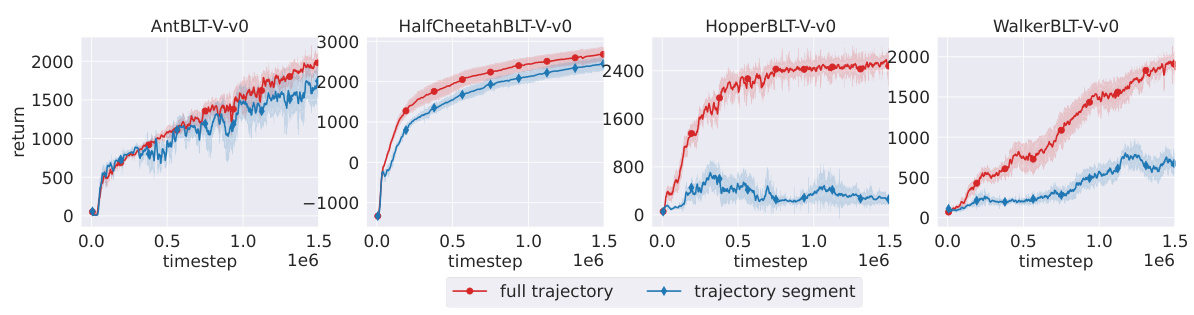
This figure compares the performance of the RESEL algorithm when trained with full trajectories versus training with trajectory segments of 64 steps. The results show that training with full trajectories generally leads to better performance, particularly in tasks with shorter trajectory lengths. However, the difference in performance between full trajectories and segments is less pronounced in tasks with longer and more cyclical trajectories (like HalfCheetahBLT-V). This suggests that using shorter trajectory segments might be sufficient for tasks with highly cyclical data, as the segments can effectively capture the properties of the full trajectory.

This figure compares the performance of RESEL using different RNN architectures (Mamba, GRU, and Transformer) for four different partially observable Markov decision process (POMDP) tasks. The y-axis represents the stochastic policy return, and the x-axis shows the training timesteps. The shaded area around each line represents the standard error. The figure shows that RESEL with different RNN architectures performs similarly across these POMDP tasks, suggesting that the choice of RNN architecture is relatively less important compared to the context-encoder-specific learning rate.

This figure shows the sensitivity analysis of the context-encoder-specific learning rates (LRCE and LRother) on the WalkerBLT-V-v0 environment. The x-axis represents different values of LRother, while LRCE is fixed at 5 × 10^-6. The y-axis represents the average final return achieved. The plot demonstrates the effect of varying the learning rate for the other layers (MLP) while keeping the learning rate for the context encoder (RNN) constant. The results suggest an optimal LRother value exists, showing that the performance is sensitive to the MLP learning rate, while being relatively insensitive to LRCE in this particular experiment.
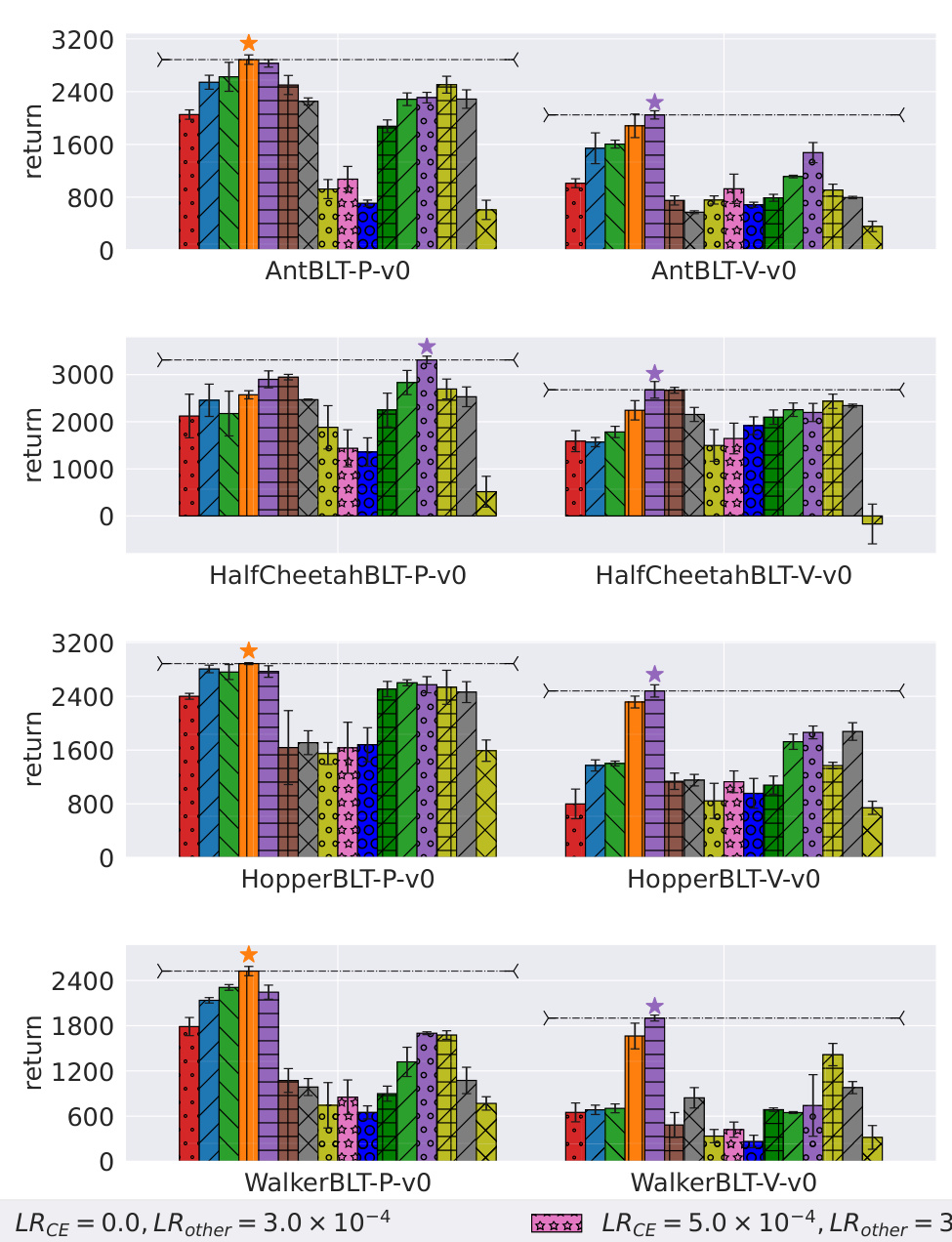
This figure shows the results of sensitivity studies on the context-encoder-specific learning rates for eight POMDP tasks. Different learning rates for the context encoder (LRCE) and other layers (LRother) were tested. Each bar represents the average final return for a particular combination of LRCE and LRother. The highest-performing variants for each task are marked with a star. The results highlight the importance of using distinct learning rates for the context encoder and other layers to achieve optimal performance in POMDP tasks.
More on tables
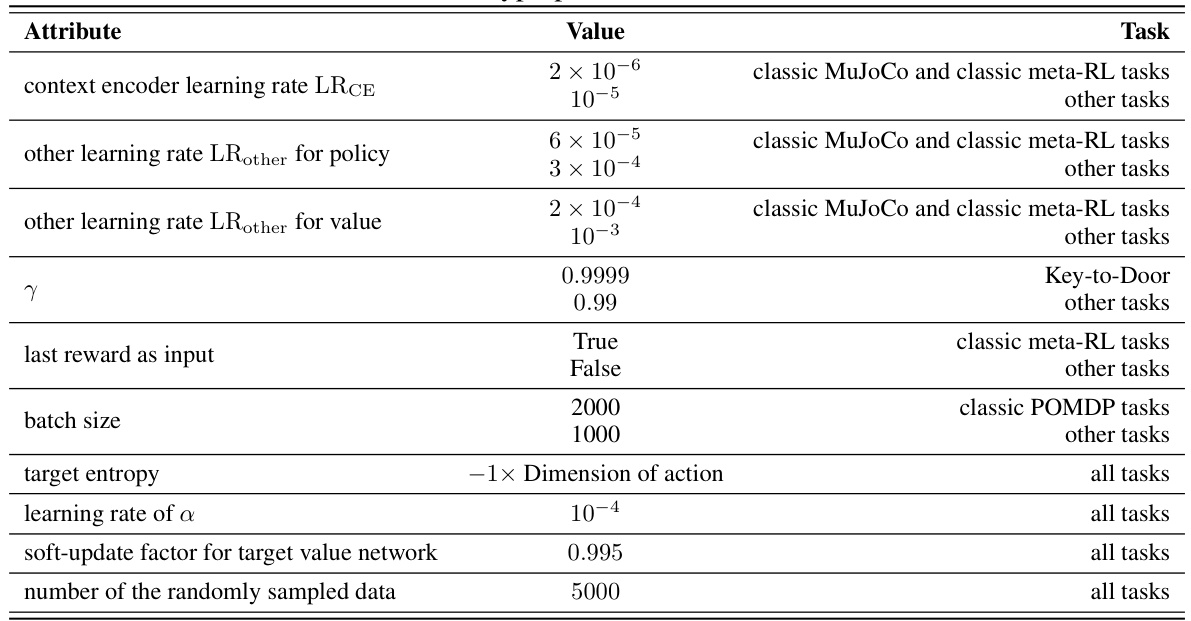
This table lists the hyperparameters used in the RESEL algorithm. Different values were used depending on the specific task (classic MuJoCo, classic meta-RL, other tasks, etc.). The hyperparameters include learning rates for the context encoder and other layers (both for policy and value networks), the discount factor (γ), whether the last reward was used as input, the batch size, target entropy, learning rate for entropy coefficient α, and soft-update factor for the target value network. The number of randomly sampled data points is also specified.
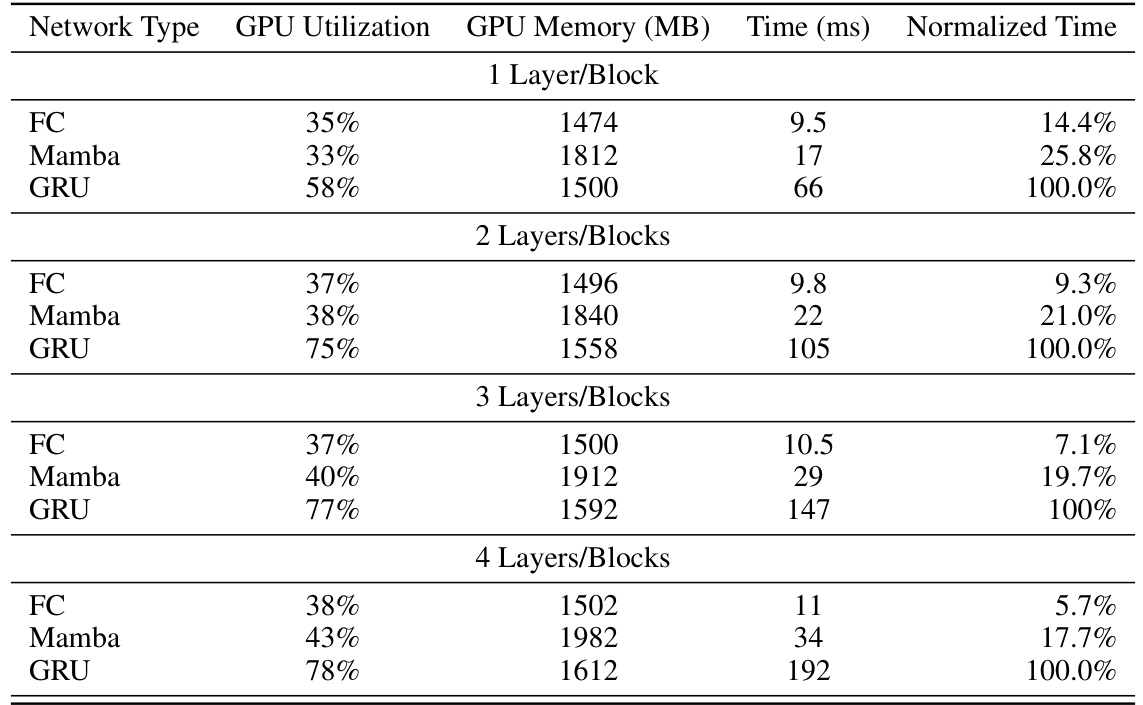
This table compares the GPU utilization, memory usage, and time cost of using fully connected (FC) networks, Mamba networks, and GRU networks as context encoders in the HalfCheetah-v2 environment. The results are broken down by the number of layers/blocks used in the context encoder (1, 2, 3, or 4). The time cost is presented in milliseconds (ms), and a normalized time is also provided relative to the GRU time cost for easier comparison. This table shows that Mamba consistently uses less GPU memory and time than GRU while maintaining comparable performance.

This table presents the average performance and standard error across six trials for different algorithms (RESEL, PPO-GRU, MF-RNN, SAC-Transformer, SAC-MLP, TD3-MLP, GPIDE-ESS, VRM, A2C-GRU) on various classic partially observable Markov decision process (POMDP) tasks. The POMDP tasks involve locomotion with gravity changes, where the gravity is not fully observable. The table shows the average return achieved by each algorithm across AntBLT-P-v0, AntBLT-V-v0, HalfCheetahBLT-P-v0, HalfCheetahBLT-V-v0, HopperBLT-P-v0, HopperBLT-V-v0, WalkerBLT-P-v0, and WalkerBLT-V-v0 tasks. The results highlight the improved performance of the RESEL algorithm compared to existing baselines.

This table presents the average performance and standard error of different reinforcement learning algorithms on five MuJoCo locomotion tasks with randomized gravity. The gravity is varied across 60 different conditions, with 40 used for training and 20 for testing. The algorithms compared are RESEL (the proposed method), SAC-MLP, SAC-GRU, ESCP, PEARL, EPI, OSI, and ProMP. The results show the average return achieved by each algorithm across the five tasks.

This table shows the average performance results on five classic MuJoCo locomotion tasks (HalfCheetah-v2, Hopper-v2, Walker2d-v2, Ant-v2, Humanoid-v2) at different training time steps (300k, 1M, and 5M). The performance is measured using several state-of-the-art reinforcement learning algorithms including TD3, SAC, TQC, TD3+OFE, TD7, and the proposed RESEL algorithm. Each entry in the table represents the average return achieved by each algorithm, along with the standard error across 6 independent trials. The table allows for a comparison of the algorithms’ performance at different training stages, indicating their learning speed and asymptotic performance.
Full paper#