↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional OOD detection methods rely on training separate generative models for each inlier distribution, which is inefficient and impractical for continual learning or resource-constrained scenarios. This necessitates the need for a more efficient and generalizable approach.
This paper introduces DiffPath, a novel OOD detection technique using a single unconditional diffusion model. It measures the rate-of-change and curvature of diffusion paths to distinguish between in-distribution and out-of-distribution samples. Experiments demonstrate that DiffPath is competitive with prior methods on various tasks, showcasing its effectiveness and potential as a more efficient solution for OOD detection.
Key Takeaways#
Why does it matter?#
This paper is important because it challenges the conventional approach to out-of-distribution (OOD) detection, which typically requires training separate models for each dataset. By demonstrating that a single, pre-trained diffusion model can effectively perform OOD detection across diverse tasks, this research opens new avenues for developing more efficient and generalizable OOD detection methods. This is particularly relevant in resource-constrained settings and continual learning scenarios where retraining models for every new dataset is impractical. The theoretical framework further enhances understanding of the underlying mechanisms, potentially leading to improved models and algorithms.
Visual Insights#

This figure visually demonstrates the core concept of the DiffPath method. It shows the diffusion paths—trajectories in the feature space—of samples from two different datasets (CIFAR10 and SVHN) as they are progressively transformed into a standard normal distribution via the DDIM (Denoising Diffusion Implicit Models) process. The key observation is that these paths exhibit varying rates of change and curvatures. The authors propose to use these path characteristics as features to distinguish between in-distribution and out-of-distribution samples, forming the basis of their OOD detection method.

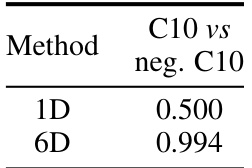
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) scores for various out-of-distribution (OOD) detection tasks. It compares the performance of the proposed DiffPath method (using ImageNet and CelebA as base distributions) against several baseline methods. Higher AUROC scores indicate better performance. The number of function evaluations (NFEs) needed by each method is also provided, where lower values are preferable.
In-depth insights#
Single DM OOD#
The concept of “Single DM OOD”—out-of-distribution detection using a single diffusion model—presents a compelling alternative to traditional methods. Existing techniques often require training a separate model for each in-distribution dataset, leading to inefficiency and scalability issues. A single, universally trained model offers significant advantages, such as reduced computational costs and improved generalization. The core idea revolves around analyzing the characteristics of diffusion paths, such as the rate of change and curvature, generated by the single model to differentiate in-distribution and out-of-distribution samples. This approach cleverly sidesteps the need for likelihood-based metrics, which have proven unreliable in many OOD scenarios. However, challenges remain. The effectiveness hinges critically on the model’s ability to meaningfully represent diverse data distributions, and the chosen statistics might need careful selection and validation for optimal performance across various tasks and datasets. Further research should focus on exploring the theoretical underpinnings of this method, particularly its connection to optimal transport and its sensitivity to different model architectures and training regimes.
DiffPath Method#
The DiffPath method ingeniously leverages a single, unconditional diffusion model for out-of-distribution (OOD) detection, a significant departure from conventional methods needing separate models for each dataset. It analyzes the characteristics of the diffusion paths connecting samples to the standard normal distribution, specifically focusing on the rate-of-change and curvature. This innovative approach avoids the need for retraining models and offers enhanced efficiency. DiffPath’s core strength lies in its ability to quantify the differences between the diffusion paths of in-distribution and out-of-distribution samples using readily computable statistics. Theoretical analysis connecting the method to optimal transport further solidifies its foundation. The method’s versatility and efficiency make it a promising advancement in the field of OOD detection, showcasing the potential of utilizing a single foundation model for multiple tasks.
OT Path Analysis#
Optimal Transport (OT) path analysis offers a novel perspective on out-of-distribution (OOD) detection. By viewing the forward diffusion process as an OT map, the method cleverly leverages the properties of the optimal transport path between data samples and the standard normal distribution. This framework provides a strong theoretical foundation, linking the characteristics of the OT path—specifically its rate-of-change and curvature—to the ability to distinguish in-distribution from out-of-distribution samples. This approach differs significantly from previous likelihood-based or reconstruction-based methods, offering a more direct analysis of the sample’s trajectory in the diffusion process. The theoretical analysis, though potentially limited by assumptions regarding the data distribution, offers valuable insights into the relationship between the diffusion paths and the KL divergence. This connection allows us to understand why the proposed OOD statistics (rate-of-change and curvature) are effective discriminators. The exploration of higher-order Taylor expansions and the resulting high-dimensional statistics further enhances the framework’s robustness and discrimination power, potentially overcoming limitations of simpler approaches.
High-D Statistic#
The concept of a ‘High-D Statistic’ in the context of out-of-distribution (OOD) detection using diffusion models is intriguing. It suggests moving beyond simple, low-dimensional metrics like likelihood or reconstruction error which may not fully capture the complexity of high-dimensional data such as images. A high-dimensional statistic would likely involve aggregating multiple features or aspects of the diffusion process, potentially capturing both the magnitude and direction of changes in the diffusion path. This approach could be more robust to variations inherent in high-dimensional spaces and better at distinguishing between in-distribution and out-of-distribution samples. The key challenge lies in finding a meaningful way to combine these diverse features into a single, effective statistic. It would be essential to consider not just the rate of change, but also higher-order derivatives or curvature of the diffusion path, to create a more comprehensive representation. Furthermore, the computational cost of computing a high-dimensional statistic needs careful consideration, especially when dealing with large datasets. The effectiveness of the approach will hinge on both its ability to discriminate effectively and its computational feasibility. Ultimately, the success of a ‘High-D Statistic’ will depend on its ability to leverage the unique characteristics of the diffusion trajectories of high-dimensional data for accurate OOD detection.
Future Works#
The paper’s exploration of out-of-distribution (OOD) detection using a single unconditional diffusion model opens several exciting avenues for future research. Extending DiffPath to other modalities beyond images (e.g., time series, audio, text) is a crucial next step, as the core concept of measuring trajectory characteristics may generalize effectively across diverse data types. A deeper investigation into higher-order Taylor expansions could potentially reveal even more nuanced and powerful OOD detection statistics, particularly within high-dimensional data. The observed performance variation depending on the training distribution of the diffusion model suggests the need for further analysis to optimize the choice of the base distribution, potentially through a more principled approach than simply using large pre-trained models. Further research into handling near-OOD scenarios, where subtle differences between inlier and outlier distributions pose challenges, is warranted. While the paper touches upon theoretical connections to optimal transport, a fuller exploration of this link could lead to more robust and principled OOD detection methodologies. Finally, a systematic comparison against alternative approaches tailored for specific domains or data characteristics could further solidify the strength of the proposed DiffPath methodology.
More visual insights#
More on figures

This figure displays histograms of three different statistics calculated for CIFAR10 and SVHN training sets. The first statistic is the negative log-likelihood (NLL) calculated using a diffusion model trained on CIFAR10. The other two statistics involve the L2 norm of the score and the L2 norm of the derivative of the score (curvature), both computed along the diffusion path from data points to the standard normal distribution using a diffusion model trained on ImageNet. The histograms visualize the distribution of these statistics for each dataset, illustrating how they differ between in-distribution (CIFAR10) and out-of-distribution (SVHN) samples.

This figure shows the forward diffusion process of samples from different datasets (CIFAR10, SVHN, CelebA) using two different pre-trained diffusion models (ImageNet and CelebA). The forward process aims to transform the samples into a standard normal distribution. Even though the models were not trained on these specific samples, they manage to bring samples close to the standard normal distribution, even though some residual features from the original image may remain. This visual demonstration supports the authors’ claim that the characteristics of these diffusion trajectories can be used as an effective indicator for out-of-distribution detection.
More on tables
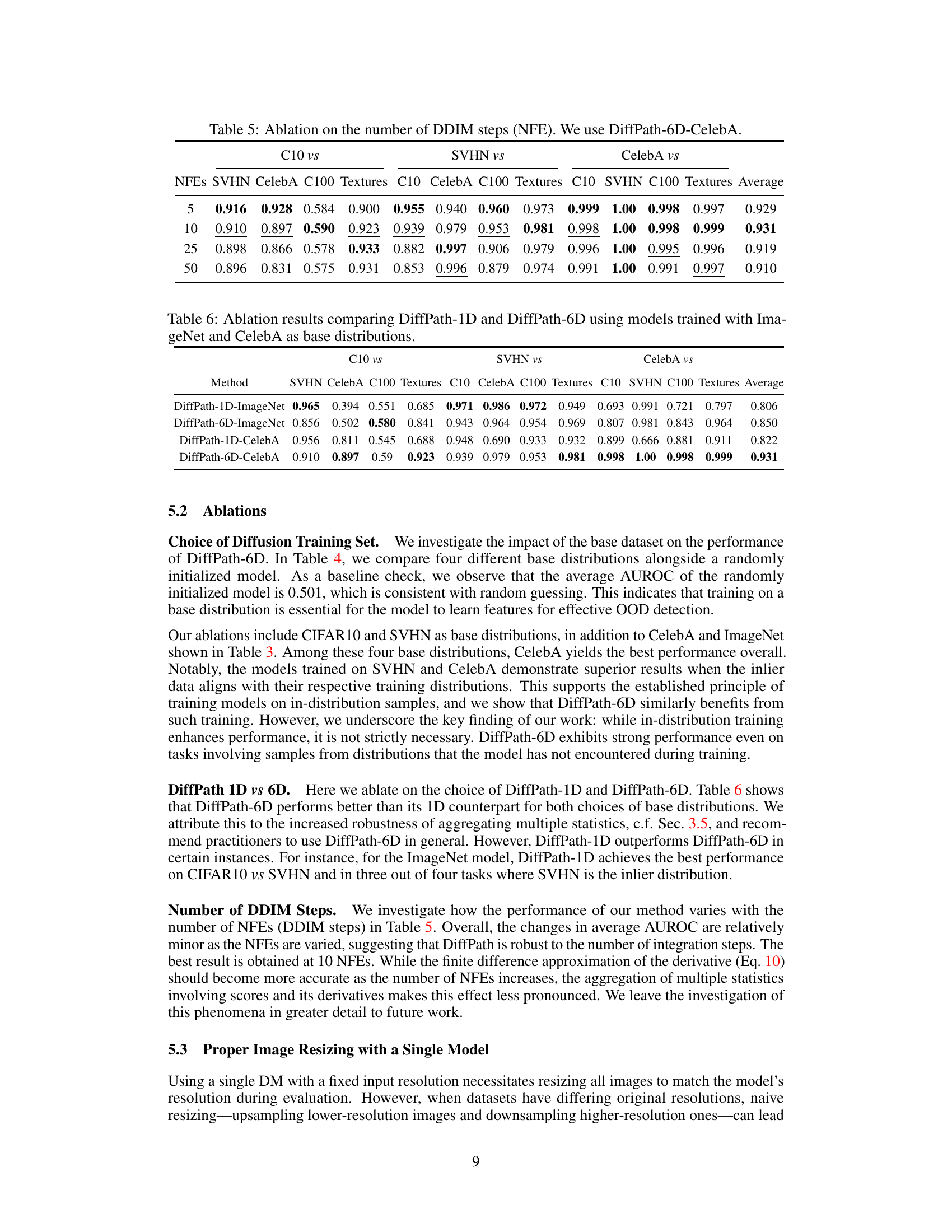
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) scores for the DiffPath-1D and DiffPath-6D methods on a specific out-of-distribution (OOD) detection task. The task involves distinguishing between CIFAR-10 images and a modified version of CIFAR-10 images where the pixel signs have been inverted (’neg. C10’). The AUROC score quantifies the performance of each method in correctly classifying these images as either in-distribution or out-of-distribution. A score of 0.5 indicates random performance, while a score of 1.0 indicates perfect performance. The table shows that DiffPath-6D significantly outperforms DiffPath-1D on this specific task.
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) scores for various out-of-distribution (OOD) detection tasks. It compares the performance of the proposed method, DiffPath (using both ImageNet and CelebA pretrained models), against several state-of-the-art baselines. Higher AUROC indicates better performance. The table also includes the number of function evaluations (NFEs), which represents the computational cost of each method.
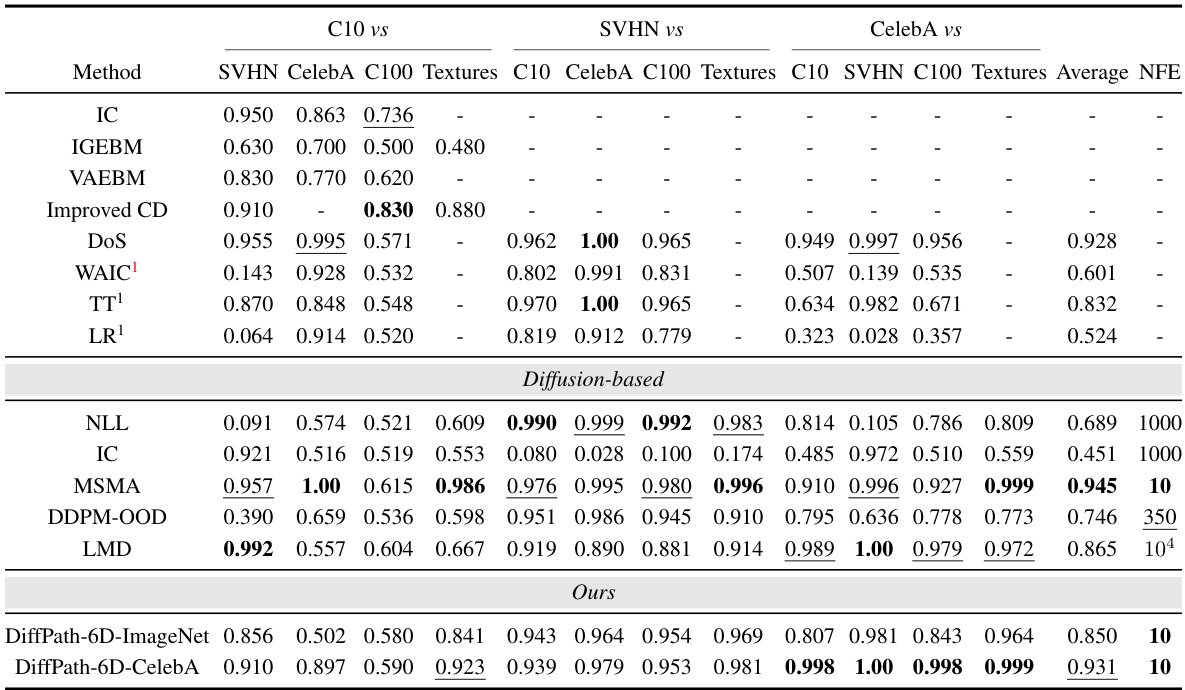
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) scores achieved by various methods on several out-of-distribution (OOD) detection tasks. The methods are tested on different combinations of in-distribution and out-of-distribution datasets. Two variants of the proposed DiffPath model (using ImageNet and CelebA as base distributions) are compared against multiple baseline methods. The number of function evaluations (NFEs) required by each method is also included. Higher AUROC scores indicate better performance, and lower NFE values indicate greater efficiency.
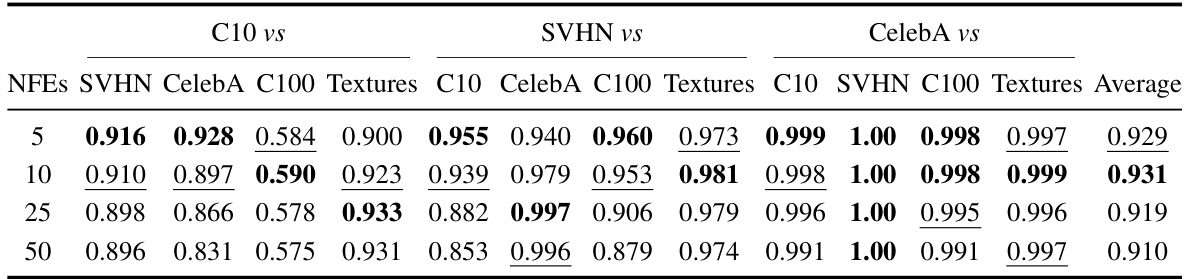
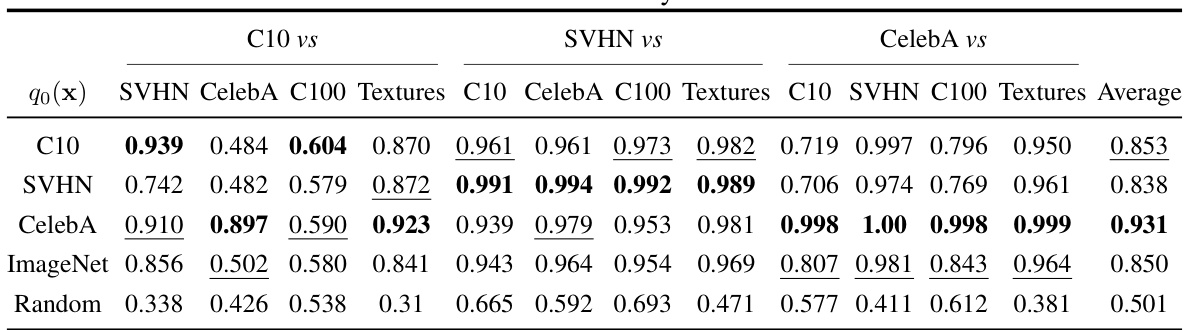
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) scores for several out-of-distribution (OOD) detection tasks. It compares the performance of the proposed DiffPath method (using ImageNet and CelebA as base distributions) against various other OOD detection methods. Higher AUROC scores indicate better performance. The table also shows the number of function evaluations (NFEs), a measure of computational cost, for the diffusion-based methods.
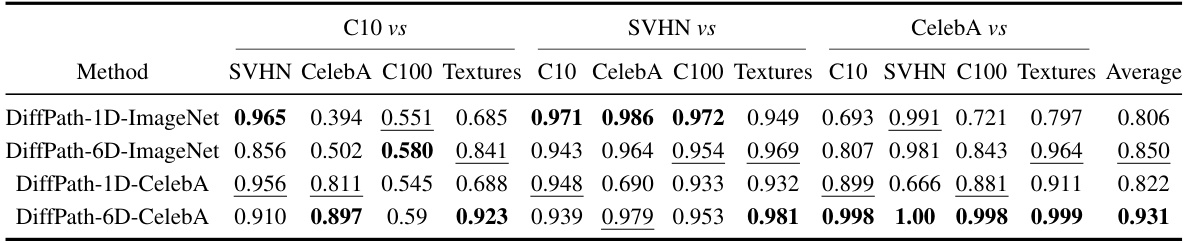
This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) scores for various out-of-distribution (OOD) detection tasks. It compares the performance of the proposed DiffPath method (using ImageNet and CelebA pre-trained models) against several baseline methods. Higher AUROC indicates better performance. The table also indicates the number of function evaluations (NFEs), a measure of computational cost, where lower is preferable. Bold and underlined entries highlight the top two performing methods for each task.

This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) scores for various out-of-distribution (OOD) detection tasks. It compares the performance of the proposed method, DiffPath (using both ImageNet and CelebA as base distributions), against several other OOD detection methods. The table shows AUROC scores for different combinations of inlier and outlier datasets and also includes the number of function evaluations (NFEs) required by each method, reflecting computational cost. Higher AUROC values indicate better performance. Bold and underlined values highlight the best and second-best performing methods for each task.
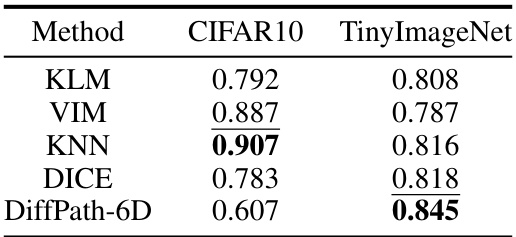
This table presents the Average AUROC scores achieved by different methods on two near-OOD tasks from the OpenOOD benchmark. The methods are compared on their ability to distinguish between in-distribution and out-of-distribution samples. The first task uses CIFAR10 as the in-distribution data and CIFAR100 and TinyImageNet as out-of-distribution datasets. The second task uses TinyImageNet as the in-distribution data, and SSB (hard split) and NINCO as out-of-distribution datasets. The results highlight the relative performance of DiffPath-6D against other state-of-the-art methods on these challenging near-OOD scenarios. Note that DiffPath-6D uses ImageNet as the base distribution and 10 DDIM steps. Bold and underlined scores indicate the best and second-best performances, respectively.
Full paper#