TL;DR#
Many real-world datasets are imbalanced or have heavy-tailed distributions, posing challenges for accurate mean estimation while preserving user-level differential privacy. Existing methods like the Winsorized Mean Estimator (WME) suffer from bias and sensitivity issues under such conditions. They often rely on clipping, which introduces bias in heavy-tailed scenarios, and struggle with imbalanced datasets that lead to larger sensitivity and thus increased estimation error.
This paper introduces a novel approach using Huber loss minimization to overcome these limitations. Huber loss adapts to the data distribution, reducing bias without relying on clipping. The adaptive weighting scheme addresses the issues caused by sample size imbalances among users. This method demonstrates significantly improved accuracy and robustness in experiments compared to existing methods, especially for challenging datasets. Theoretical analysis provides guarantees on privacy and error bounds.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and machine learning, offering a novel approach to mean estimation under user-level differential privacy. Its adaptive strategy for handling imbalanced datasets and heavy-tailed distributions significantly improves the accuracy and robustness of privacy-preserving algorithms. This opens avenues for more reliable federated learning systems and other distributed applications.
Visual Insights#
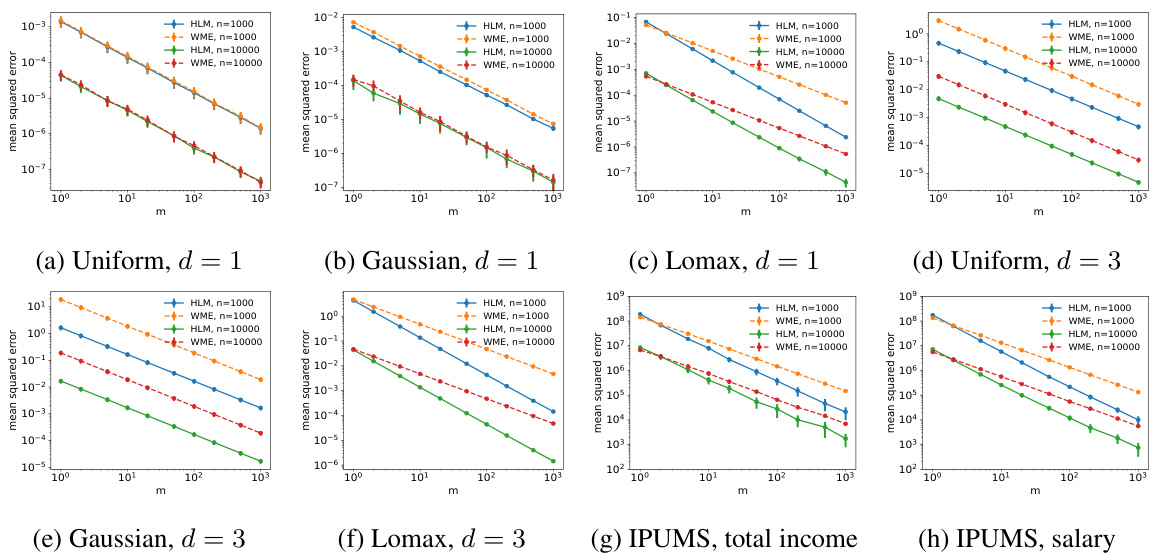
🔼 This figure shows the convergence of the mean squared error for the Huber loss minimization approach (HLM) and the Winsorized Mean Estimator (WME) methods under different sample sizes (m) and numbers of users (n), for balanced users (i.e., all users have the same number of samples). The results are presented for four different data distributions: uniform, Gaussian, Lomax, and IPUMS datasets (total income and salary). Different dimensionalities (d=1 and d=3) are considered, demonstrating how HLM performs better for heavy-tailed distributions (Lomax and IPUMS).
read the caption
Figure 1: Convergence of mean squared error with balanced users.
Full paper#



















