TL;DR#
Machine learning models often lack reliable uncertainty quantification. Conformal prediction provides prediction intervals with guaranteed marginal coverage, but often suffers from suboptimal conditional coverage and excessive interval length. This limits their practical use in high-stakes applications like medical diagnosis. Prior work has attempted to improve these shortcomings through model retraining or modification.
This paper introduces a post-training method called “boosted conformal prediction.” This novel approach uses gradient boosting to refine an existing conformity score function to achieve improved conditional coverage and shorter intervals. This allows for improved prediction quality without needing to modify the pre-trained model itself. The approach shows superior performance compared to conventional methods across several benchmark datasets, reducing interval length and improving conditional coverage.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly improves conformal prediction, a crucial method for quantifying uncertainty in machine learning models. It introduces a novel boosting technique that enhances existing methods by improving both the accuracy of prediction intervals and their precision. This addresses a key challenge in machine learning: building reliable and informative uncertainty quantification that directly benefits various applications such as medical diagnosis and financial forecasting.
Visual Insights#
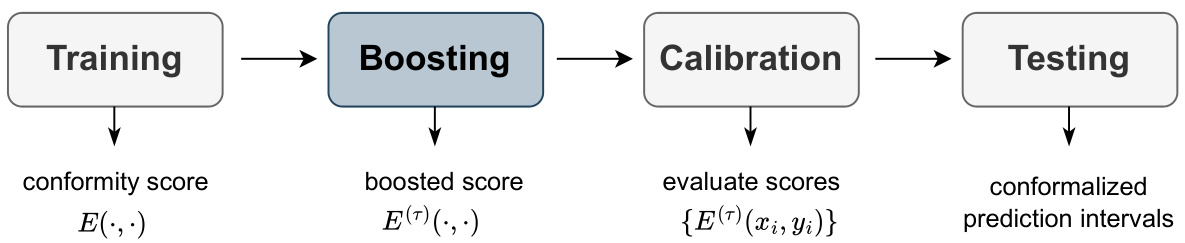
🔼 This figure illustrates the steps involved in the boosted conformal prediction procedure. It begins with a training phase producing a conformity score, followed by a boosting stage that enhances this score using gradient boosting. The number of boosting rounds is determined via cross-validation to optimize performance. Subsequently, a calibration phase evaluates the boosted scores, which are finally used in the testing phase to construct conformalized prediction intervals.
read the caption
Figure 1: Illustration of the boosted conformal prediction procedure. We introduce a boosting stage between training and calibration, where we boost τ rounds on the conformity score function E(·, ·) and obtain the boosted score E(†)(·,·). The number of boosting rounds τ is selected via cross-validation. A detailed description of the procedure is presented in Algorithm 1.
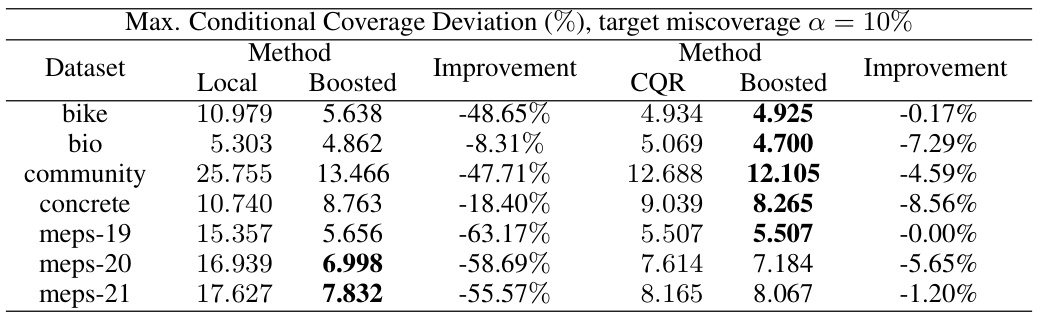
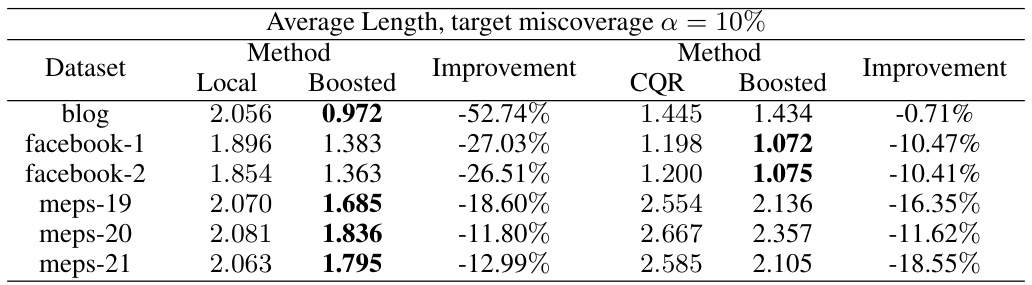
🔼 This table presents the maximum conditional coverage deviation (lM) for different conformal prediction methods (Local, Boosted Local, CQR, Boosted CQR) across various datasets. The deviation measures how far the conditional coverage of the prediction intervals deviates from the target coverage rate (10%). Lower values indicate better performance. The ‘Improvement’ column shows the percentage reduction in lM achieved by the boosted methods compared to their respective baselines.
read the caption
Table 1: Test set maximum deviation loss lM evaluated on various conformalized intervals. The best result achieved for each dataset is highlighted in bold.
In-depth insights#
Boosted Conformal#
The concept of “Boosted Conformal” prediction intervals presents a powerful approach to enhance the reliability and efficiency of conformal prediction methods. It leverages the strengths of conformal prediction’s distribution-free validity while addressing limitations such as potentially large interval lengths or deviations from target coverage. The core idea is to improve a base conformity score function using machine learning techniques, such as gradient boosting, post-training. This allows for targeted improvements in interval properties without altering the original model, thus maintaining its existing predictive capabilities. A crucial aspect is the design of loss functions tailored to specific desired properties (like shorter intervals or better conditional coverage). The method’s post-training nature offers flexibility and avoids computationally expensive retraining. Empirical results show significant gains compared to standard conformal approaches. However, the selection of the base conformity score and tuning parameters, along with the potential computational cost of boosting, should be considered. Future research directions include exploring different boosting algorithms and loss functions, further investigating its properties under different distributional assumptions, and extending the approach to handle various types of prediction tasks.
Conditional Coverage#
Conditional coverage in conformal prediction addresses the crucial issue of ensuring prediction interval validity not just marginally (across all data points), but also conditionally (for specific subsets of data based on feature values). Standard conformal methods guarantee marginal coverage, but may fail to provide reliable conditional coverage. This is problematic in real-world applications where model uncertainty often varies significantly depending on input features. The paper explores techniques to improve conditional coverage, recognizing the inherent challenges and limitations. Achieving exact conditional coverage is generally impossible without strong distributional assumptions. Therefore, the focus shifts to minimizing deviation from the target conditional coverage level, potentially employing machine learning methods such as gradient boosting to refine conformity scores. The goal is to tailor prediction intervals to specific input characteristics, enhancing their practical value and reliability. The experiments demonstrate that boosting techniques can lead to substantial improvements in reducing deviations from the desired conditional coverage, thereby making conformal prediction more suitable for applications requiring precise uncertainty quantification for specific conditions.
Boosting for Length#
The section ‘Boosting for Length’ presents a compelling approach to enhance conformal prediction intervals by directly targeting interval length. Instead of relying solely on existing conformity scores, the authors propose a boosting procedure to search for optimal scores within a generalized family. This family encompasses various existing methods, providing flexibility while maintaining the theoretical guarantees of conformal prediction. The approach cleverly uses gradient boosting to iteratively improve the score function based on a differentiable length loss function, avoiding the need for retraining the base model. The key advantage lies in the post-hoc nature of the procedure, which is computationally efficient and model-agnostic. Cross-validation is employed to prevent overfitting during the boosting stage, ensuring robustness. This method shows promise in yielding shorter prediction intervals, surpassing the performance of existing methods in many cases, though it importantly acknowledges the inherent trade-off with potential undercoverage of extremely short intervals.
Empirical Results#
The empirical results section of a research paper is crucial for validating the claims made by the authors. A strong empirical results section will present findings in a clear and concise manner, clearly demonstrating that the proposed method or model outperforms existing approaches or achieves a new state-of-the-art. It is important to consider the metrics used to evaluate performance, ensuring that they are relevant and appropriate to the research question. The results should be presented visually using figures and tables, in addition to being discussed in the text. The analysis should go beyond simply reporting the results, instead offering interpretations and explanations. A good empirical results section will also discuss any limitations or potential biases in the data or methodology to provide a balanced perspective and guide future research. The choice of datasets and the methodology used for the experiment greatly impact the validity and generalizability of the findings; therefore, a thoughtful explanation of those factors is required. Finally, the empirical results should directly support the claims presented in the paper’s abstract and introduction.
Future Directions#
Future research could explore several promising avenues. Extending the boosted conformal procedure to handle more complex data structures, such as time series or graphs, would broaden its applicability. Investigating alternative boosting algorithms beyond gradient boosting might improve efficiency or robustness. A particularly interesting direction is developing theoretical guarantees for conditional coverage under weaker assumptions than those currently employed, making the method more widely applicable. Finally, incorporating user-specified preferences into the loss function would enable the creation of customized prediction intervals tailored to specific application needs, offering greater flexibility and control.
More visual insights#
More on figures
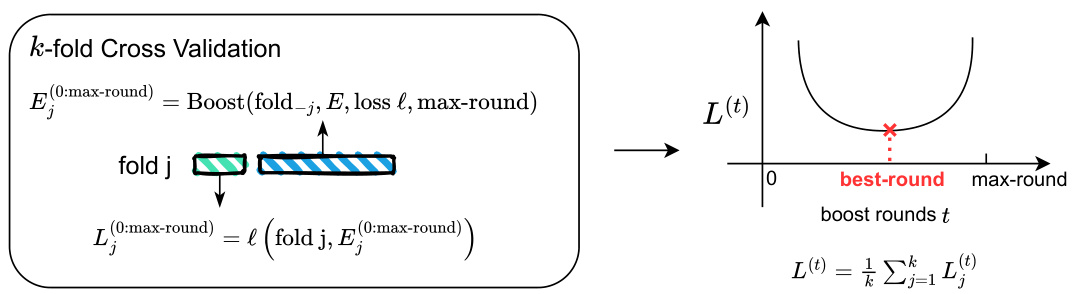
🔼 This figure illustrates the process of selecting the optimal number of boosting rounds using k-fold cross-validation. The left panel shows how the data is split into k folds, with one fold held out for validation in each iteration. A gradient boosting algorithm is applied to the remaining k-1 folds to generate a sequence of candidate score functions. The performance of each candidate is evaluated on the held-out fold using a task-specific loss function. The right panel shows a plot of the average loss across all k folds as a function of the number of boosting rounds. The round that minimizes this average loss is selected as the optimal number of boosting rounds.
read the caption
Figure 2: Schematic drawing showing the selection of the number of boosting rounds via cross-validation. Left: we hold out fold j, and use the remaining k − 1 folds to generate candidate scores E(t), t = 0, ..., max-round. The performance of each score is evaluated on fold j using the loss function l. Right: best-round minimizes the average loss across all k folds. A detailed description of the procedure is presented in Algorithm 1.
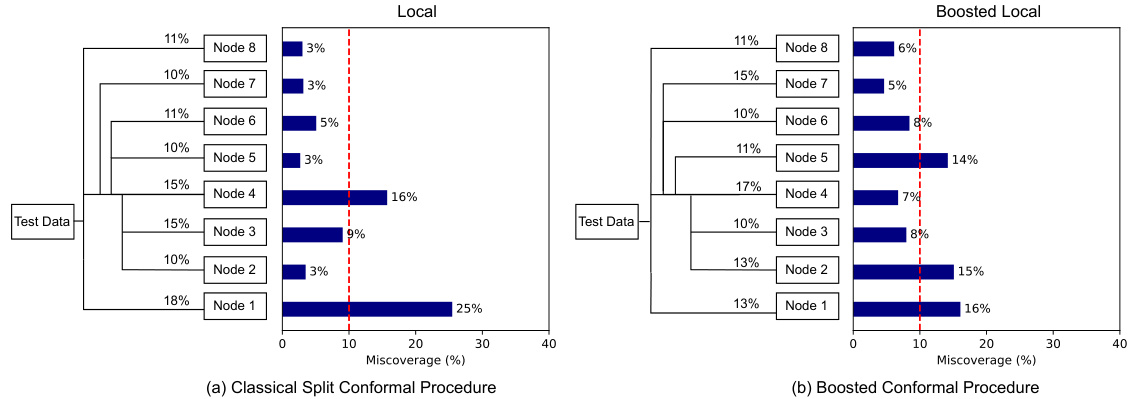
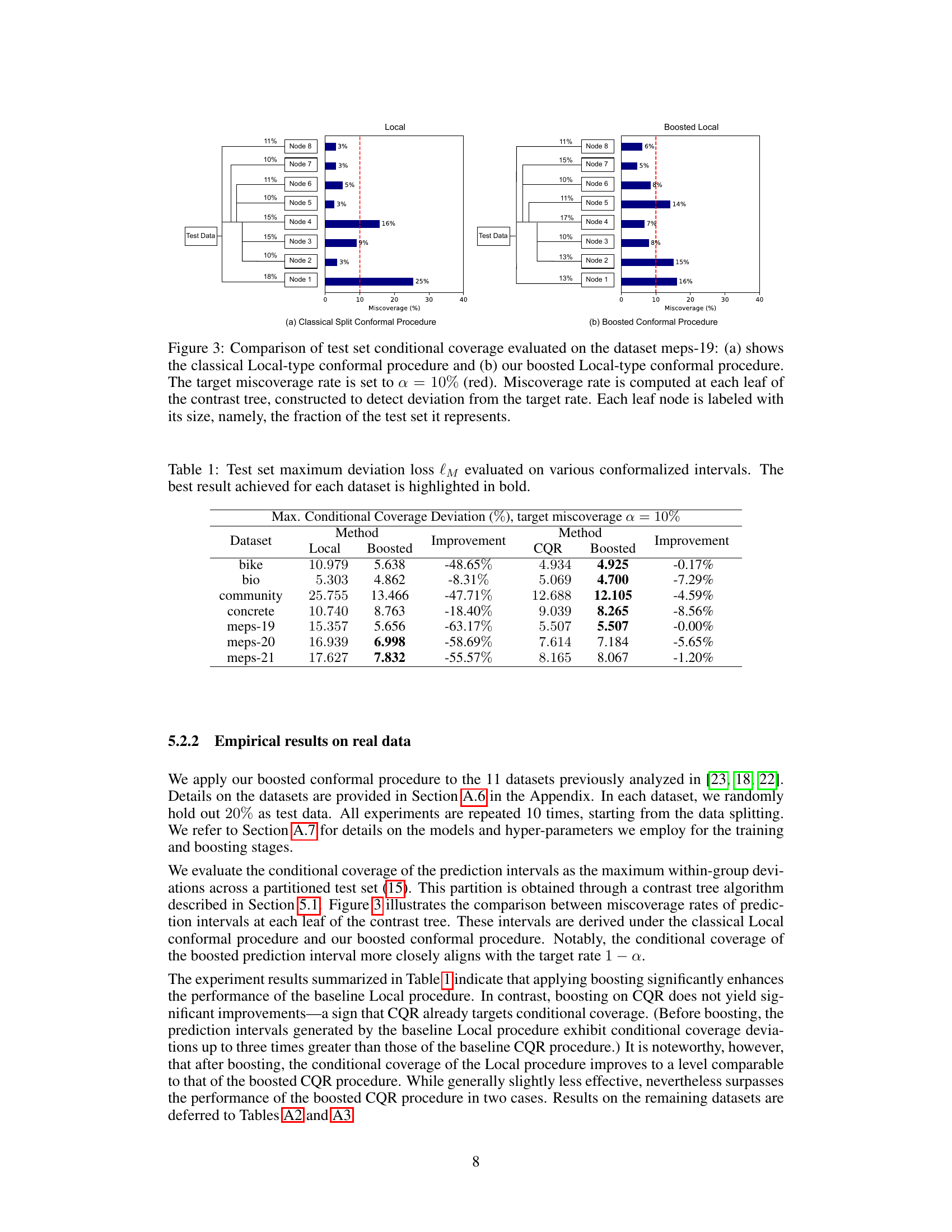
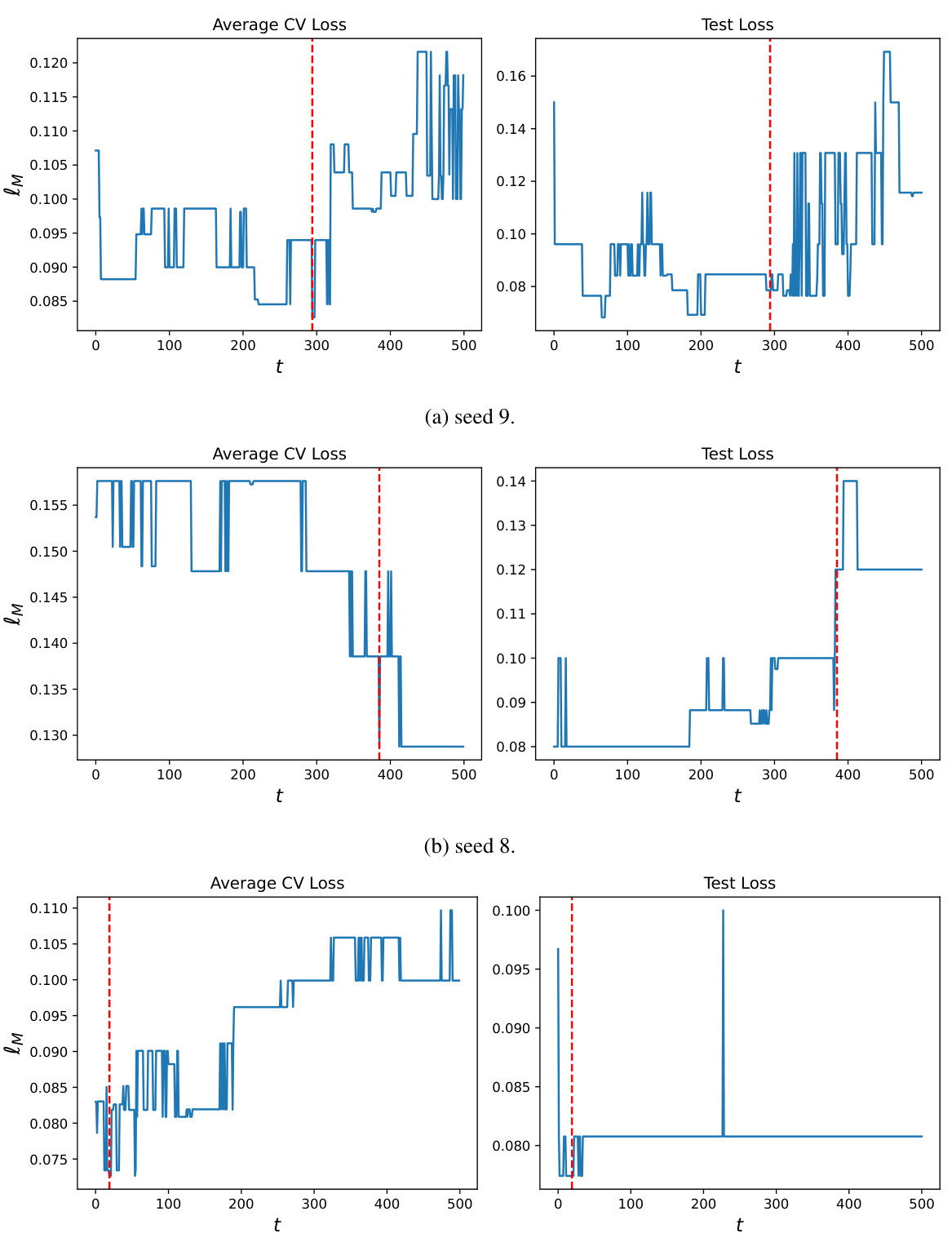
🔼 This figure compares the conditional coverage of the classical Local conformal procedure and the boosted Local conformal procedure on the meps-19 dataset. A contrast tree is used to partition the test set into leaf nodes, and the miscoverage rate (deviation from the target rate of 10%) is calculated for each leaf node. The figure visually demonstrates how the boosted procedure improves conditional coverage by showing a more even distribution of miscoverage across the leaf nodes, closer to the target rate of 10%.
read the caption
Figure 3: Comparison of test set conditional coverage evaluated on the dataset meps-19: (a) shows the classical Local-type conformal procedure and (b) our boosted Local-type conformal procedure. The target miscoverage rate is set to a = 10% (red). Miscoverage rate is computed at each leaf of the contrast tree, constructed to detect deviation from the target rate. Each leaf node is labeled with its size, namely, the fraction of the test set it represents.
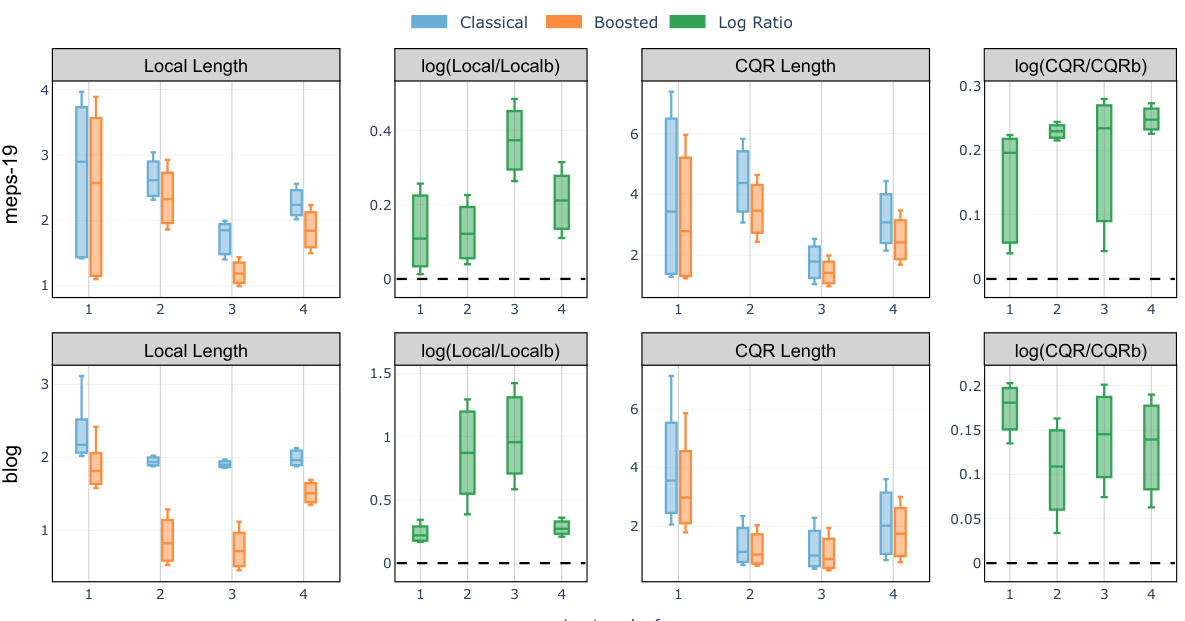
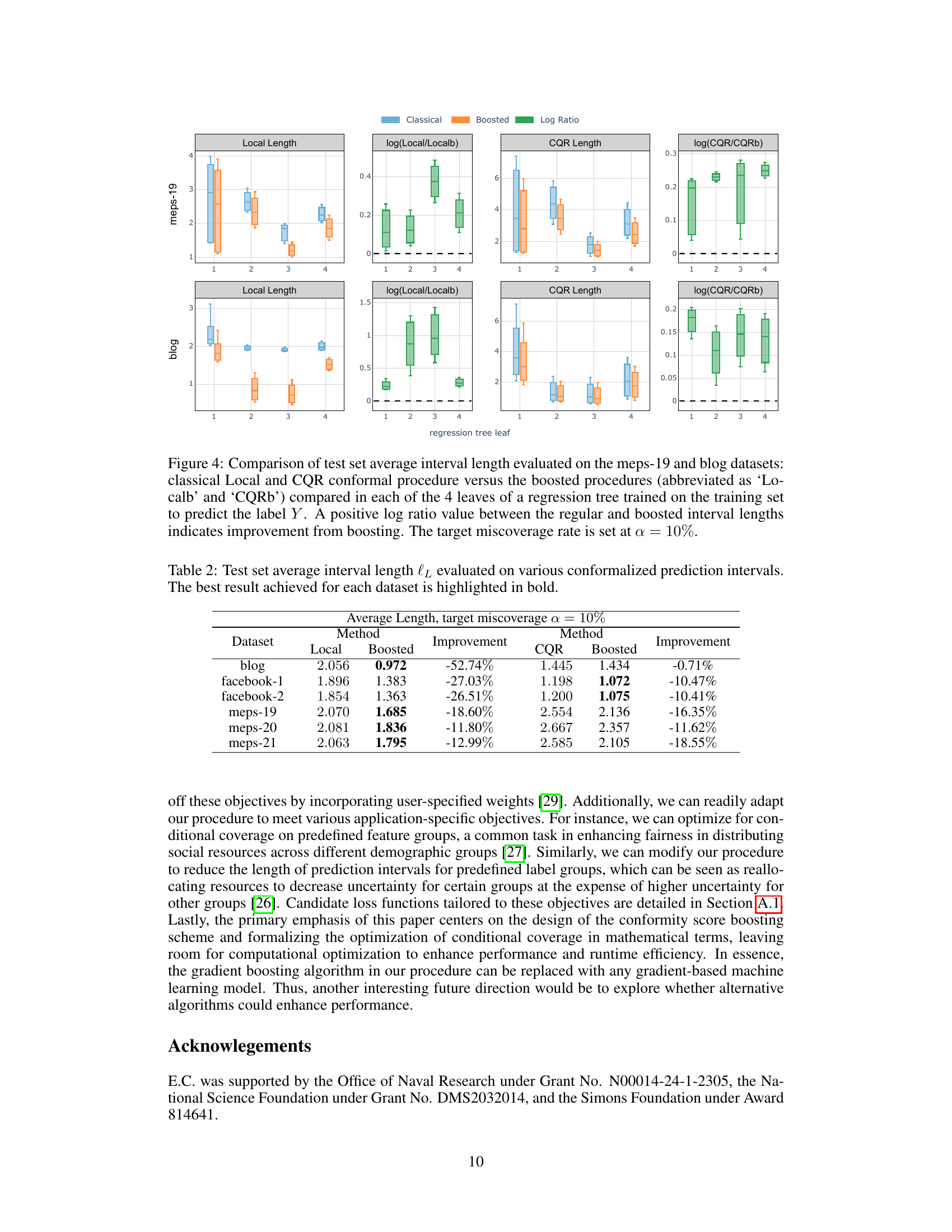
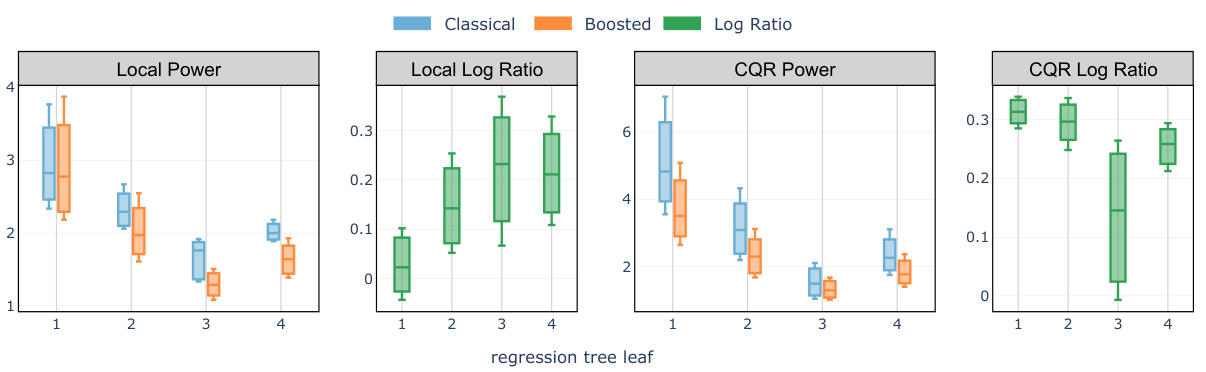
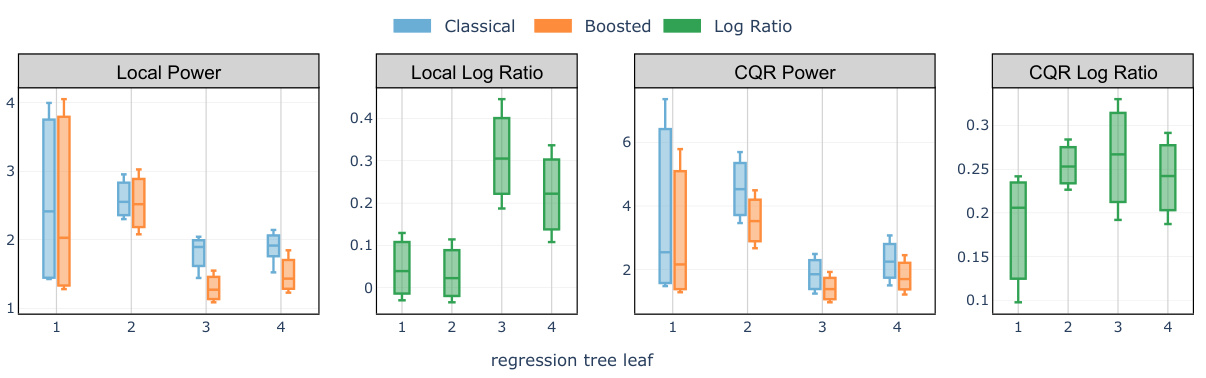
🔼 The figure compares the average interval lengths of the classical Local and CQR conformal methods with their boosted counterparts. The comparison is broken down across four leaves of a regression tree built from the training data to illustrate how the interval lengths vary across different segments of the feature space. A positive log ratio indicates that boosting reduced the interval length, signifying the effectiveness of the proposed boosting technique.
read the caption
Figure 4: Comparison of test set average interval length evaluated on the meps-19 and blog datasets: classical Local and CQR conformal procedure versus the boosted procedures (abbreviated as 'Localb' and 'CQRb') compared in each of the 4 leaves of a regression tree trained on the training set to predict the label Y. A positive log ratio value between the regular and boosted interval lengths indicates improvement from boosting. The target miscoverage rate is set at α = 10%.
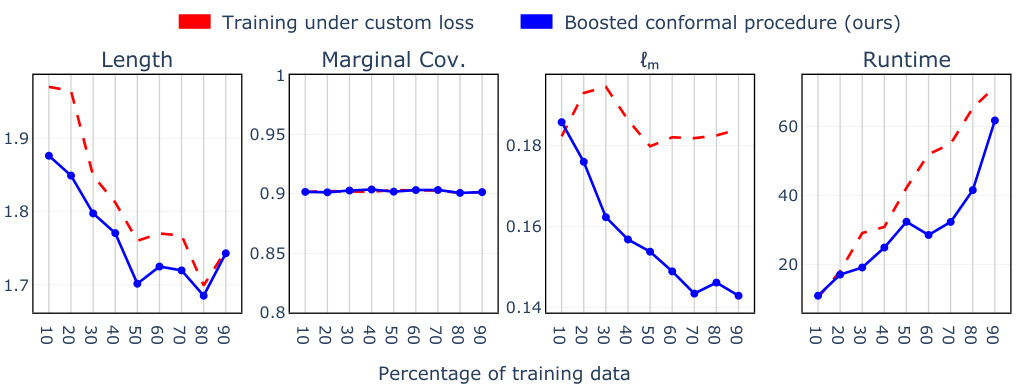
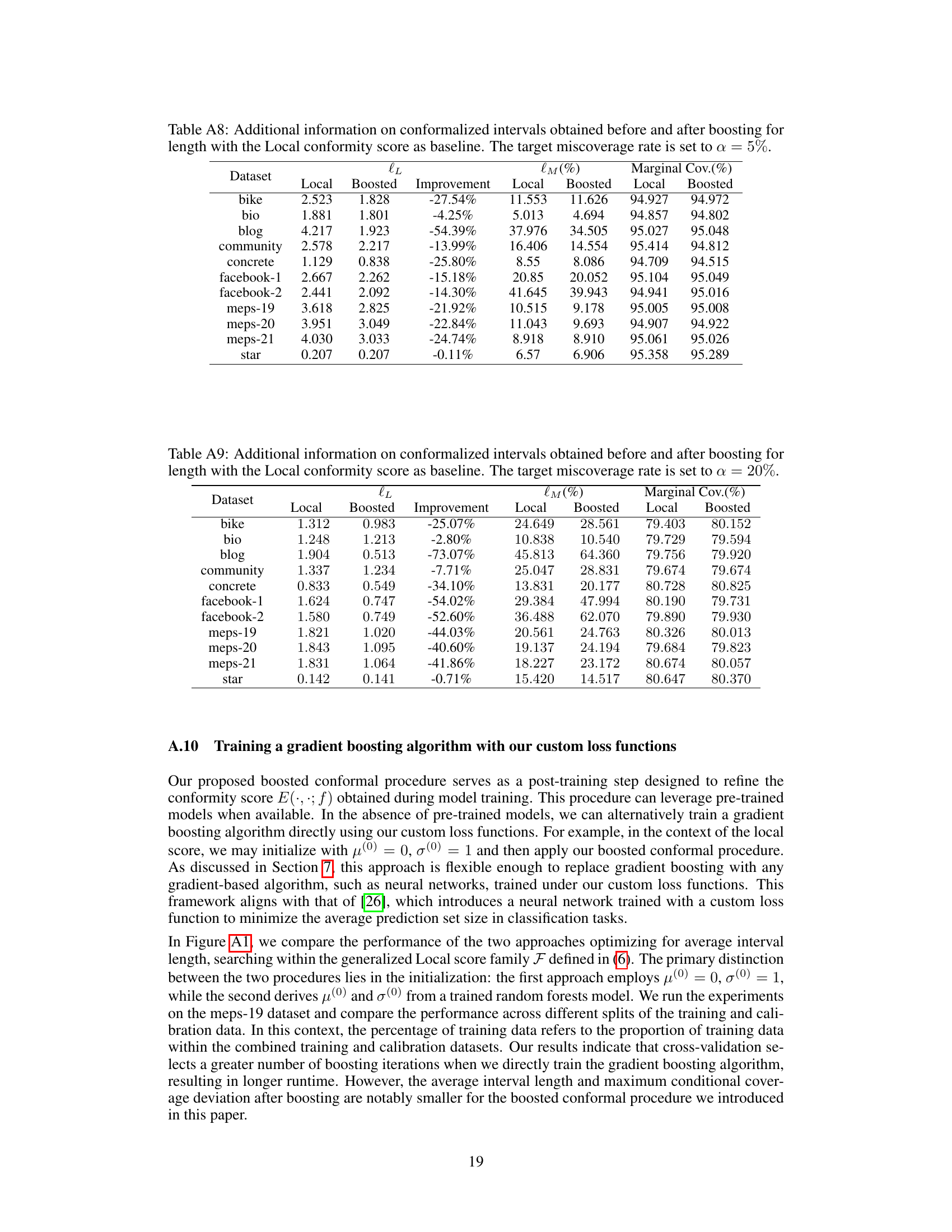
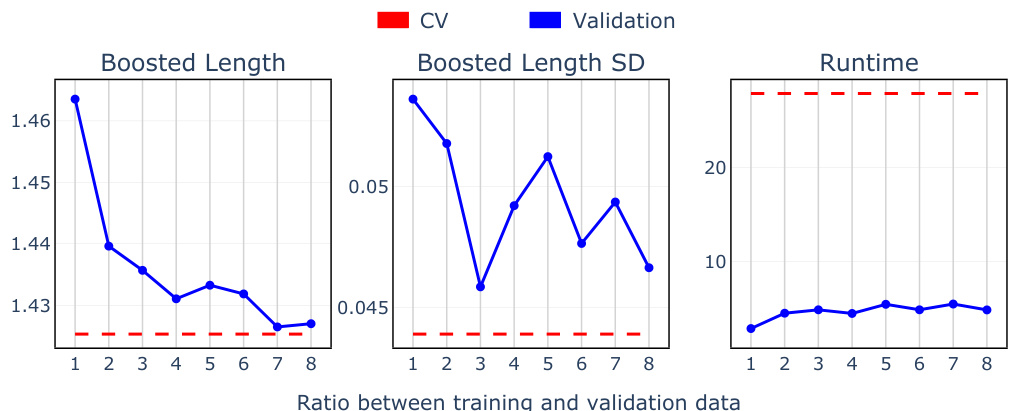
🔼 This figure compares the performance of two different approaches for optimizing conformal prediction intervals. The first, shown in red, involves directly training a gradient-based algorithm to minimize a custom loss function. The second approach, shown in blue, uses the proposed boosted conformal procedure. The x-axis represents the percentage of training data used, while the y-axis shows the average interval length, marginal coverage, maximum deviation from target conditional coverage, and training time. The figure illustrates that the boosted conformal method achieves comparable performance to the direct training method with significantly less computation time. In particular, the boosted approach shows consistent marginal coverage across different training sizes, unlike the direct training approach.
read the caption
Figure A1: Comparison of boosted interval length, marginal coverage, maximum conditional coverage deviation (lm), and runtime between direct training of a gradient-based algorithm (red) and boosting on a pre-trained conformity score (blue).
🔼 This figure illustrates the process of selecting the optimal number of boosting rounds using k-fold cross-validation. The left panel shows how, for each fold (j), a model is trained on k-1 folds, and candidate scores E(t) are generated for various boosting rounds (t). Each score’s performance is then evaluated on the held-out fold (j) using a loss function (l). The right panel displays how the best number of boosting rounds is chosen by selecting the boosting round (τ) which minimizes the average loss across all folds. Algorithm 1 provides a detailed description of this process.
read the caption
Figure 2: Schematic drawing showing the selection of the number of boosting rounds via cross-validation. Left: we hold out fold j, and use the remaining k - 1 folds to generate candidate scores E(t), t = 0, ..., max-round. The performance of each score is evaluated on fold j using the loss function l. Right: best-round minimizes the average loss across all k folds. A detailed description of the procedure is presented in Algorithm 1.
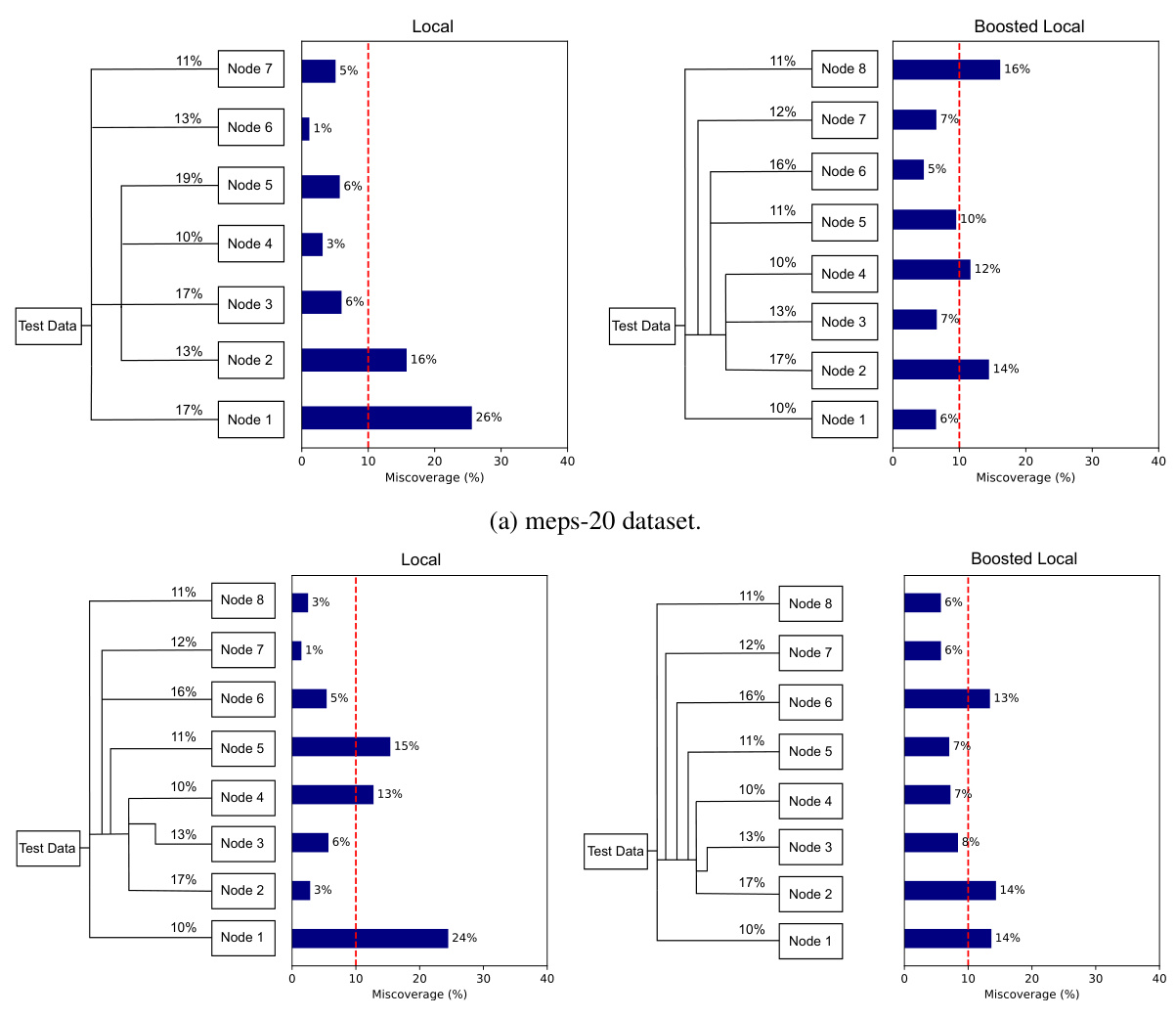
🔼 This figure compares the conditional coverage of the classical Local conformal prediction method with the proposed boosted Local method on the meps-19 dataset. The target miscoverage rate is 10%. A contrast tree is used to partition the test data, and the miscoverage rate (deviation from the target rate) is calculated for each leaf node of the tree. The figure visually shows how the boosted method improves the conditional coverage compared to the classical method by showing that the miscoverage rates are closer to the target 10% in the boosted method.
read the caption
Figure 3: Comparison of test set conditional coverage evaluated on the dataset meps-19: (a) shows the classical Local-type conformal procedure and (b) our boosted Local-type conformal procedure. The target miscoverage rate is set to α = 10% (red). Miscoverage rate is computed at each leaf of the contrast tree, constructed to detect deviation from the target rate. Each leaf node is labeled with its size, namely, the fraction of the test set it represents.

🔼 This figure compares the performance of the classical Local conformal prediction method and the proposed boosted Local method on the meps-19 dataset. Conditional coverage, the probability that the prediction interval contains the true value given specific features, is evaluated using a contrast tree which partitions the data into leaf nodes. The figure visualizes the miscoverage rate (deviation from the target 10% miscoverage rate) for each leaf node of the contrast tree. It shows that the boosted method achieves a better approximation of the target miscoverage rate.
read the caption
Figure 3: Comparison of test set conditional coverage evaluated on the dataset meps-19: (a) shows the classical Local-type conformal procedure and (b) our boosted Local-type conformal procedure. The target miscoverage rate is set to α = 10% (red). Miscoverage rate is computed at each leaf of the contrast tree, constructed to detect deviation from the target rate. Each leaf node is labeled with its size, namely, the fraction of the test set it represents.
🔼 This figure compares the conditional coverage of the classical Local conformal procedure and the boosted Local conformal procedure on the meps-19 dataset. The target miscoverage rate is 10%, represented by red lines. The contrast tree partitions the data, and each leaf node shows the conditional miscoverage rate and the percentage of the test set it represents, illustrating how well the procedures maintain the target miscoverage rate across different subsets of the data. The boosted procedure demonstrates improved alignment with the target rate.
read the caption
Figure 3: Comparison of test set conditional coverage evaluated on the dataset meps-19: (a) shows the classical Local-type conformal procedure and (b) our boosted Local-type conformal procedure. The target miscoverage rate is set to a = 10% (red). Miscoverage rate is computed at each leaf of the contrast tree, constructed to detect deviation from the target rate. Each leaf node is labeled with its size, namely, the fraction of the test set it represents.
🔼 This figure compares the conditional coverage of the classical Local conformal procedure with the boosted Local conformal procedure on the meps-19 dataset. A contrast tree is used to partition the test set into subgroups based on feature values. Each leaf of the tree represents a subgroup, and the miscoverage rate (deviation from the target 10% miscoverage rate) is calculated for each subgroup. The figure visually demonstrates the improvement in conditional coverage achieved by the boosted method by showing that the miscoverage rates in the leaves of the contrast tree for the boosted method are closer to the target rate than for the classical method.
read the caption
Figure 3: Comparison of test set conditional coverage evaluated on the dataset meps-19: (a) shows the classical Local-type conformal procedure and (b) our boosted Local-type conformal procedure. The target miscoverage rate is set to a = 10% (red). Miscoverage rate is computed at each leaf of the contrast tree, constructed to detect deviation from the target rate. Each leaf node is labeled with its size, namely, the fraction of the test set it represents.
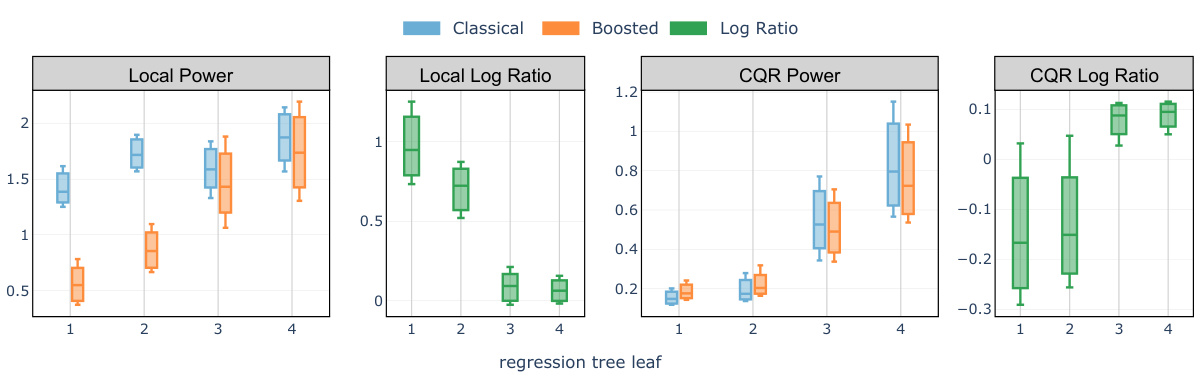
🔼 This figure compares the average interval length of classical Local and CQR conformal methods with their boosted counterparts. The comparison is shown for each of four leaves of a regression tree built to predict the target variable Y, allowing for a visualization of the impact of boosting on interval length across different regions of the feature space. A positive log ratio indicates that boosting improved the length of the prediction intervals. The target miscoverage rate used was 10%.
read the caption
Figure 4: Comparison of test set average interval length evaluated on the meps-19 and blog datasets: classical Local and CQR conformal procedure versus the boosted procedures (abbreviated as 'Localb' and 'CQRb') compared in each of the 4 leaves of a regression tree trained on the training set to predict the label Y. A positive log ratio value between the regular and boosted interval lengths indicates improvement from boosting. The target miscoverage rate is set at a = 10%.
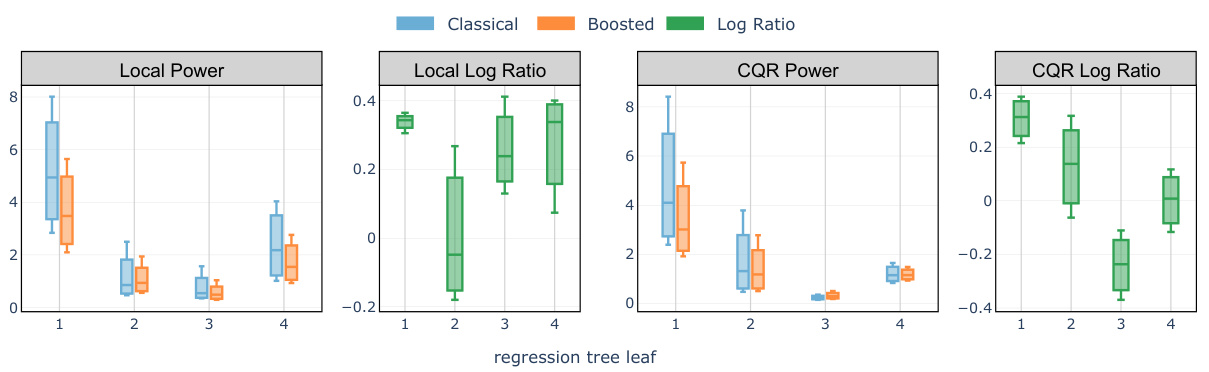
🔼 The figure compares the average interval lengths produced by classical Local and CQR conformal methods and their boosted counterparts. The comparison is done for each leaf of a regression tree trained on the training data to predict the response variable Y. A positive log ratio indicates that the boosted method produced shorter intervals than the corresponding non-boosted method. The target miscoverage rate (the probability that the true value falls outside the prediction interval) is set to 10%.
read the caption
Figure 4: Comparison of test set average interval length evaluated on the meps-19 and blog datasets: classical Local and CQR conformal procedure versus the boosted procedures (abbreviated as 'Localb' and 'CQRb') compared in each of the 4 leaves of a regression tree trained on the training set to predict the label Y. A positive log ratio value between the regular and boosted interval lengths indicates improvement from boosting. The target miscoverage rate is set at a = 10%.
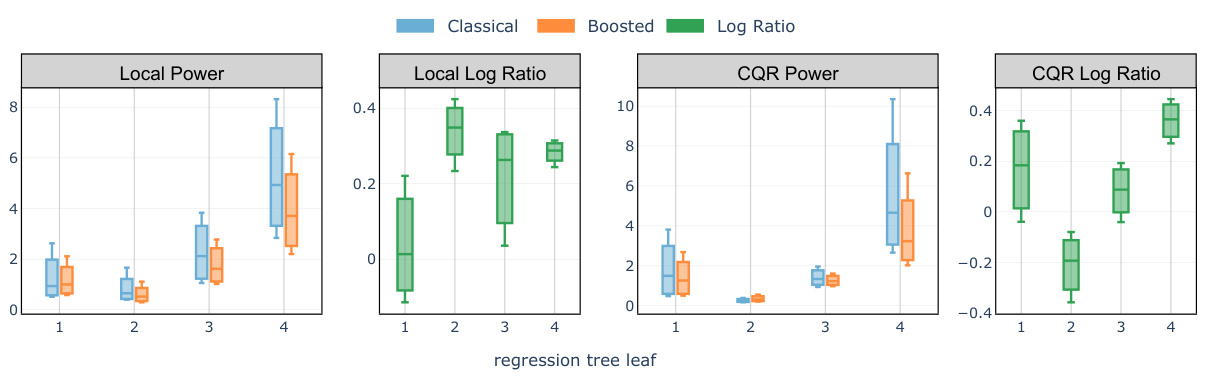
🔼 This figure compares the average interval lengths of classical and boosted conformal methods (Local and CQR) across four different leaf nodes of a regression tree. The regression tree is used to partition the data based on features, allowing for a more detailed analysis of the interval lengths under different feature combinations. Positive log ratios indicate that the boosted methods provide shorter intervals than their classical counterparts. The target miscoverage rate is set at 10%.
read the caption
Figure 4: Comparison of test set average interval length evaluated on the meps-19 and blog datasets: classical Local and CQR conformal procedure versus the boosted procedures (abbreviated as 'Localb' and 'CQRb') compared in each of the 4 leaves of a regression tree trained on the training set to predict the label Y. A positive log ratio value between the regular and boosted interval lengths indicates improvement from boosting. The target miscoverage rate is set at a = 10%.
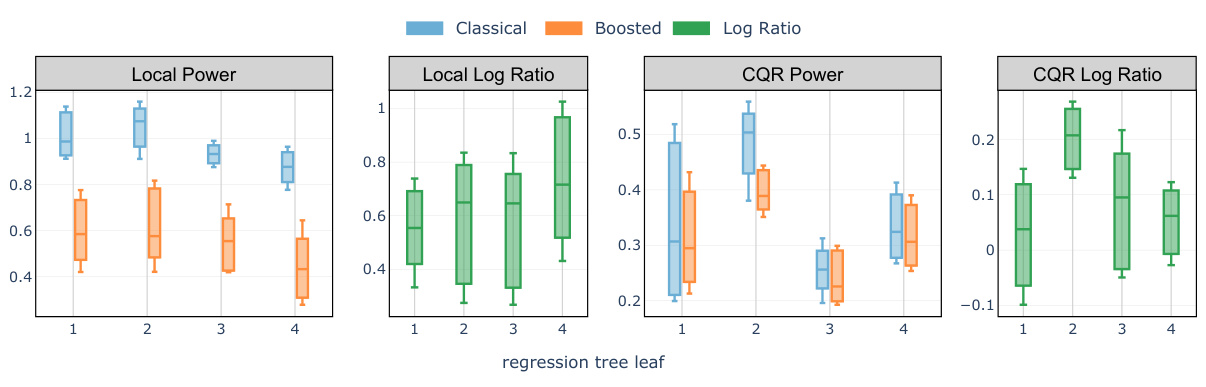
🔼 This figure compares the average interval length of the classical Local and CQR conformal methods with their boosted counterparts. The comparison is done for each of the four leaves of a regression tree built to predict the outcome variable Y. A positive log ratio indicates that boosting has led to shorter intervals. The target miscoverage rate used is 10%.
read the caption
Figure 4: Comparison of test set average interval length evaluated on the meps-19 and blog datasets: classical Local and CQR conformal procedure versus the boosted procedures (abbreviated as ‘Localb’ and ‘CQRb’) compared in each of the 4 leaves of a regression tree trained on the training set to predict the label Y. A positive log ratio value between the regular and boosted interval lengths indicates improvement from boosting. The target miscoverage rate is set at α = 10%.
🔼 This figure compares the conditional coverage of the classical Local conformal procedure and the boosted Local conformal procedure on the meps-19 dataset. A contrast tree is used to partition the test set, and the miscoverage rate (deviation from the target 10% miscoverage rate) is computed for each leaf node. The figure shows that the boosted conformal procedure achieves better conditional coverage than the classical procedure.
read the caption
Figure 3: Comparison of test set conditional coverage evaluated on the dataset meps-19: (a) shows the classical Local-type conformal procedure and (b) our boosted Local-type conformal procedure. The target miscoverage rate is set to a = 10% (red). Miscoverage rate is computed at each leaf of the contrast tree, constructed to detect deviation from the target rate. Each leaf node is labeled with its size, namely, the fraction of the test set it represents.
More on tables
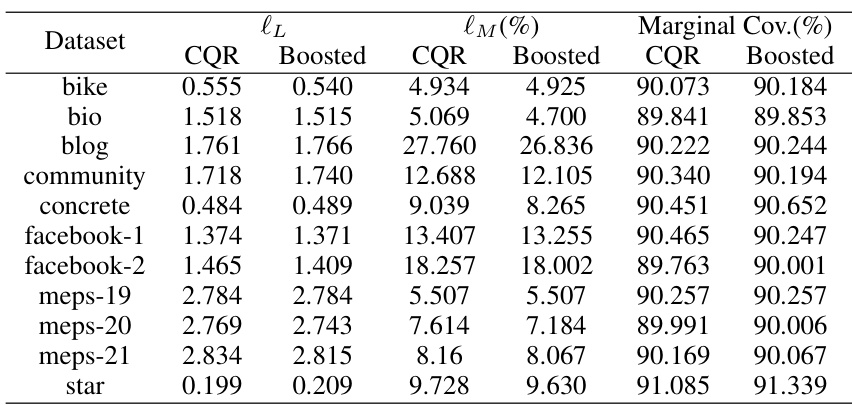
🔼 This table presents the maximum deviation of the conformalized prediction intervals from the target conditional coverage rate (1-α) for various datasets using different methods. The maximum deviation is calculated using a contrast tree algorithm. The table shows the results for both the Local and CQR methods, both before and after boosting. The best result is highlighted in bold for each dataset.
read the caption
Table 1: Test set maximum deviation loss evaluated on various conformalized intervals. The best result achieved for each dataset is highlighted in bold.

🔼 This table presents the maximum deviation loss (lM) for various conformal prediction intervals on a test dataset. The loss function quantifies the deviation from the target conditional coverage. The table compares the performance of Local, Boosted Local, CQR, and Boosted CQR methods across several datasets, highlighting the best performing method for each. The results showcase the effectiveness of boosting in improving conditional coverage for Local conformal prediction intervals, while showing that CQR methods already perform well and boosting provides less improvement.
read the caption
Table 1: Test set maximum deviation loss lM evaluated on various conformalized intervals. The best result achieved for each dataset is highlighted in bold.
🔼 This table presents the maximum conditional coverage deviation (lM) for different conformal methods (Local, Boosted Local, CQR, Boosted CQR) across various datasets. The lower the lM value, the closer the conditional coverage is to the target, indicating better performance. The table shows both the performance of standard conformal methods and their boosted counterparts, allowing for a comparison of improvement achieved through boosting.
read the caption
Table 1: Test set maximum deviation loss lM evaluated on various conformalized intervals. The best result achieved for each dataset is highlighted in bold.
🔼 This table presents the results of evaluating the maximum deviation loss (lM) for various conformal prediction intervals across different datasets. The loss lM measures how much the conditional coverage of the prediction intervals deviates from the target coverage rate. The table compares the performance of Local, Boosted Local, CQR, and Boosted CQR methods. The best performing method for each dataset is highlighted in bold, indicating the method that achieved the lowest deviation from the target conditional coverage rate.
read the caption
Table 1: Test set maximum deviation loss lM evaluated on various conformalized intervals. The best result achieved for each dataset is highlighted in bold.
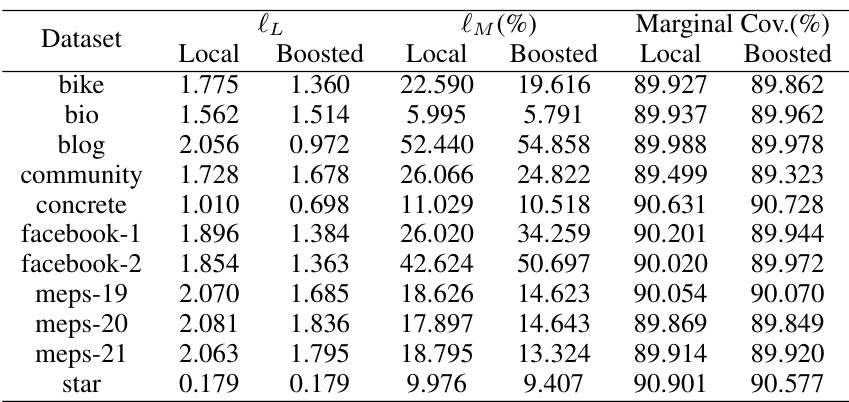
🔼 This table presents the maximum deviation from the target conditional coverage rate (10%) for various conformal prediction intervals. It compares the performance of the Local and CQR methods, both with and without boosting, across multiple datasets. The ‘Improvement’ column shows the percentage reduction in deviation achieved by boosting. Lower values indicate better performance, with bold values representing the best result for each dataset.
read the caption
Table 1: Test set maximum deviation loss \(\ell_M\) evaluated on various conformalized intervals. The best result achieved for each dataset is highlighted in bold.
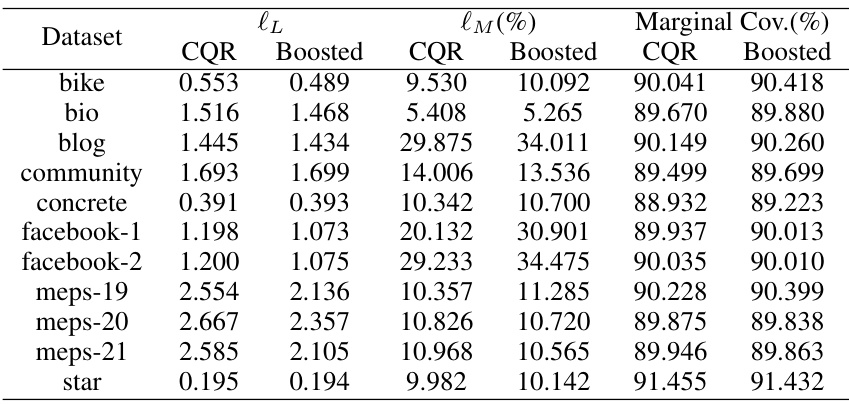
🔼 This table presents the maximum deviation from the target conditional coverage rate (1-α) for various conformal prediction intervals. The deviation is calculated using a contrast tree method. Results are shown for both the Local and CQR conformity scores, both before and after applying the boosting procedure. The table helps to evaluate the effectiveness of the boosting method in improving the accuracy of conditional coverage.
read the caption
Table 1: Test set maximum deviation loss lM evaluated on various conformalized intervals. The best result achieved for each dataset is highlighted in bold.
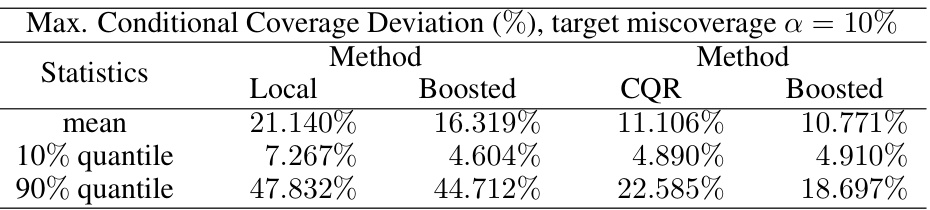
🔼 This table presents the maximum deviation from the target conditional coverage rate (1-α = 0.9) for various conformalized prediction intervals on eleven different datasets. The methods compared are Local, Boosted Local, CQR, and Boosted CQR. The best performing method for each dataset is highlighted in bold. The results show the effectiveness of the boosted conformal methods in reducing the deviation from the target coverage rate compared to the non-boosted versions, especially for the Local method.
read the caption
Table 1: Test set maximum deviation loss lM evaluated on various conformalized intervals. The best result achieved for each dataset is highlighted in bold.
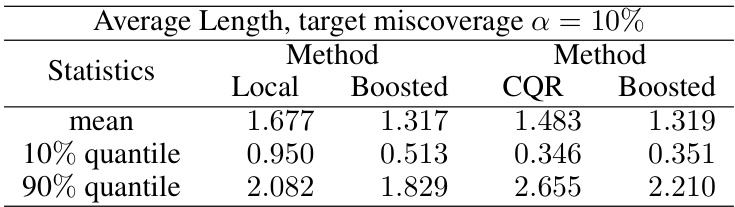
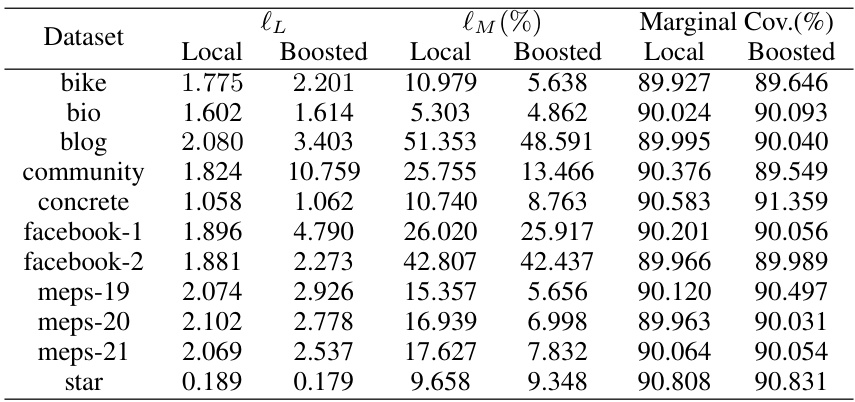
🔼 This table presents the average length of prediction intervals obtained using different methods: Local, Boosted Local, CQR, and Boosted CQR. The results are shown for 11 different datasets. The ‘best’ result for each dataset (shortest interval length) is highlighted in bold. The table demonstrates the impact of the boosting procedure on interval length, showing improvements in many cases.
read the caption
Table 2: Test set average interval length l₁ evaluated on various conformalized prediction intervals. The best result achieved for each dataset is highlighted in bold.
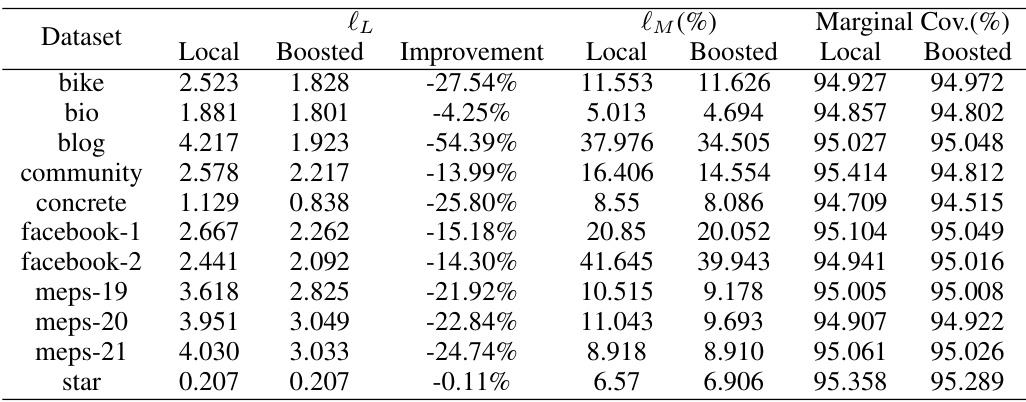
🔼 This table presents the results of evaluating the maximum deviation loss (lm) for different conformalized prediction intervals. It shows the performance of the Local and CQR methods, both with and without boosting, on various datasets. The best performing method for each dataset is highlighted in bold, offering a concise comparison of different approaches to conformal prediction.
read the caption
Table 1: Test set maximum deviation loss evaluated on various conformalized intervals. The best result achieved for each dataset is highlighted in bold.
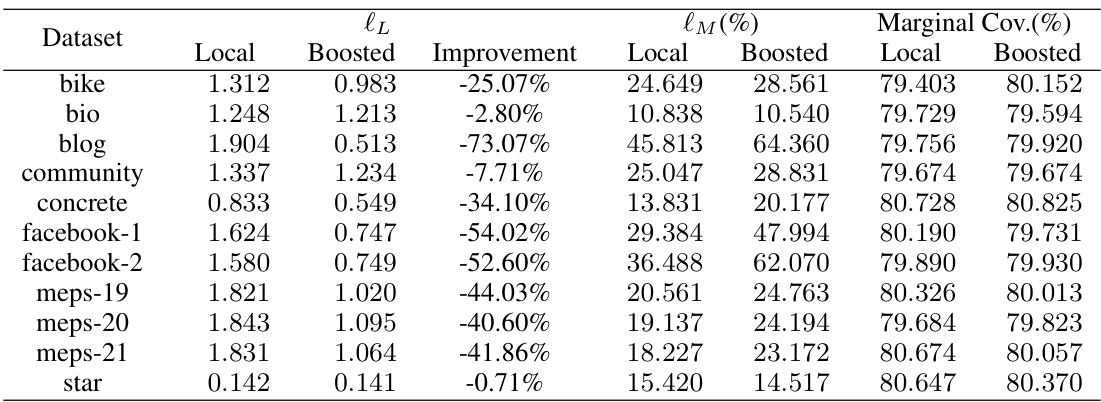
🔼 This table presents the maximum conditional coverage deviation (lM) for different datasets using various conformal prediction interval methods. The methods compared include Local, Boosted Local, CQR, and Boosted CQR. The table shows the lM values for each method and dataset, and highlights the best performing method for each dataset in bold, indicating the method with the lowest deviation from the target conditional coverage.
read the caption
Table 1: Test set maximum deviation loss lM evaluated on various conformalized intervals. The best result achieved for each dataset is highlighted in bold.
Full paper#