↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Equivariant neural networks (ENNs) excel in tasks with known data symmetries. However, optimizing ENNs is notoriously difficult, often requiring extensive hyperparameter tuning. Existing methods address this by approximating equivariance or through careful regularization. These methods, however, don’t directly address the core optimization problem, leaving room for improvement.
This work proposes a novel framework that tackles the optimization problem head-on. By relaxing the hard equivariance constraint during training and progressively constraining it until reaching an equivariant solution, they enable optimization over a significantly larger hypothesis space. This approach leads to improved generalization performance on several ENN architectures, demonstrating its effectiveness across different datasets and tasks. The results suggest a promising new direction for training high-performing ENNs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with equivariant neural networks. It offers a novel solution to a persistent challenge—the difficulty in training such models—by introducing a constraint relaxation technique that significantly improves optimization and generalization performance. This opens exciting new avenues for research and development in various applications of equivariant models, particularly those facing data scarcity or requiring careful hyperparameter tuning.
Visual Insights#

This figure compares standard training of equivariant neural networks (NNs) with the proposed training method using constraint relaxation. Standard training restricts the optimization process to a limited parameter space, potentially hindering performance. The proposed method introduces an additional non-equivariant term during training, expanding the search space to include approximately equivariant networks. At testing, the model is projected back into the equivariant space, aiming for a better solution than standard training.

This table presents the mean absolute error (MAE) for energy and force prediction using the Equiformer model, both with and without the proposed optimization framework. The results are shown for four different molecules from the MD17 dataset. The MAE values are reported in milli-electron volts (meV) for energy and milli-electron volts per Ångström (meV/Å) for forces.
In-depth insights#
Equivariant Optimization#
Equivariant neural networks, while powerful for tasks with inherent symmetries, often suffer from optimization difficulties. The core challenge lies in the constrained parameter space imposed by the equivariance constraint, limiting the model’s ability to explore a wider range of potential solutions. This paper proposes a novel framework that addresses this limitation by introducing a constraint relaxation technique during training. This relaxation, achieved by adding a non-equivariant term to intermediate layers, effectively expands the optimization landscape. A crucial aspect is the gradual re-introduction of the constraint, ensuring convergence to an equivariant solution while harnessing the benefits of the expanded search space. The approach employs regularization techniques, such as the Lie derivative, to control the magnitude of the relaxation and prevent divergence from equivariance. This innovative approach demonstrably improves the generalization performance of equivariant models across various architectures, offering a significant advancement in training efficiency and model accuracy. The work provides a thorough empirical analysis showcasing performance gains, supporting its claim of enhancing optimization within the realm of equivariant networks.
Constraint Relaxation#
The concept of ‘Constraint Relaxation’ in the context of equivariant model training presents a powerful technique to improve model optimization. The core idea is to temporarily loosen the strict equivariance constraints during training, allowing the model to explore a wider range of solutions in a larger hypothesis space. This relaxation, achieved by introducing additional non-equivariant terms in the network, helps to overcome the optimization difficulties often associated with equivariant models. By gradually tightening these constraints over the course of training, the model can converge to an approximately equivariant solution. The approach cleverly uses the advantages of a larger search space while still retaining the benefits of equivariance. It addresses the challenge of optimization difficulty in equivariant networks by introducing a method to refine the solution in a controlled manner, which leads to better generalization performance.
Lie Derivative Reg.#
The heading ‘Lie Derivative Reg.’ strongly suggests a regularization technique leveraging Lie derivatives within a machine learning model, likely for tasks involving geometric data or symmetries. Lie derivatives measure the rate of change of a tensor field along a flow, making them ideal for handling transformations. In this context, the regularization likely penalizes deviations from desired equivariance properties. This implies the model’s parameters are constrained to maintain a specific behavior under transformations, and the Lie derivative measures the violation of this constraint. The method aims for better generalization by enforcing equivariance and potentially alleviating optimization challenges common in equivariant models. The effectiveness would depend on factors like the choice of Lie group, the metric employed for the penalty, and how this is incorporated within the overall training process. The ‘reg’ likely suggests the use of a penalty term in the loss function that incorporates Lie derivatives. This is important for practical implementation.
Projection Error#
The concept of “Projection Error” in the context of equivariant neural networks is crucial. It arises from the method of relaxing the equivariance constraint during training to facilitate optimization and then projecting the learned model back into the equivariant subspace during testing. This projection, however, isn’t perfect. The projection error quantifies the difference between the model obtained after this projection and the model that would have resulted from training directly in the restricted equivariant space. A small projection error indicates that the relaxation strategy was effective, yielding a model close to the optimal equivariant solution, while a large error suggests that the relaxation might have diverted training too far from the desired space. Controlling this error is paramount to ensure the benefits of enhanced optimization outweigh the potential loss in equivariance and generalization performance. Techniques such as regularization terms to constrain the model’s distance from the target space and schedules for gradually enforcing equivariance during training are key to mitigating the projection error. Therefore, minimizing the projection error is vital for successfully leveraging constraint relaxation to improve the training of equivariant networks.
Future Directions#
Future research could explore several promising avenues. Improving the theoretical understanding of the proposed constraint relaxation framework is crucial, potentially by leveraging empirical process theory to rigorously analyze optimization error. Extending the framework to encompass broader classes of symmetry groups, beyond matrix Lie groups and discrete groups, would significantly expand applicability. Investigating the impact of various regularization strategies and scheduling techniques on convergence behavior and generalization performance deserves further investigation. Finally, exploring the effectiveness of this framework on more complex and high-dimensional tasks, such as large-scale molecular dynamics simulations or weather forecasting, would provide valuable insights into the method’s scalability and robustness.
More visual insights#
More on figures
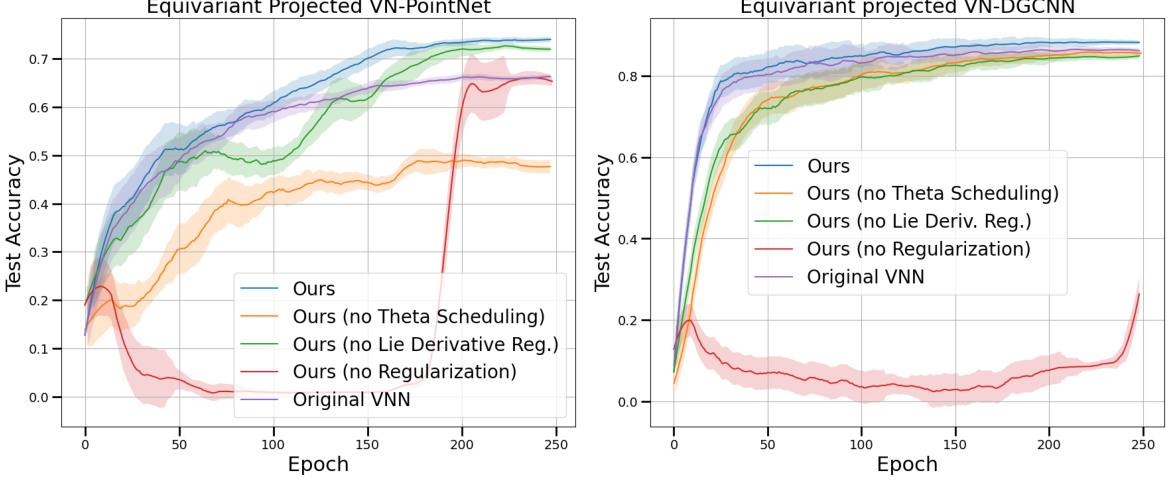
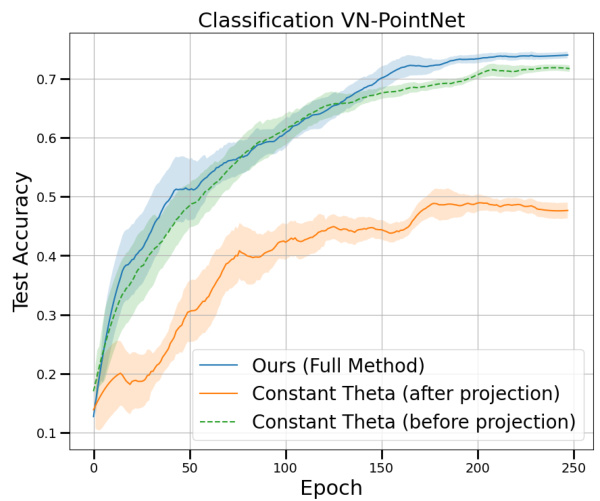
This figure shows the test accuracy for the ModelNet40 classification task during the training process for two different equivariant neural networks: PointNet and DGCNN. Five different training methods are compared: the proposed method with and without different components (theta scheduling, Lie derivative regularization, and overall regularization), and the original training method for the baseline. Notably, the accuracy is calculated for the equivariant models after projection into the equivariant space. This highlights the performance improvement achieved by the proposed optimization framework, especially in comparison to the original training method.
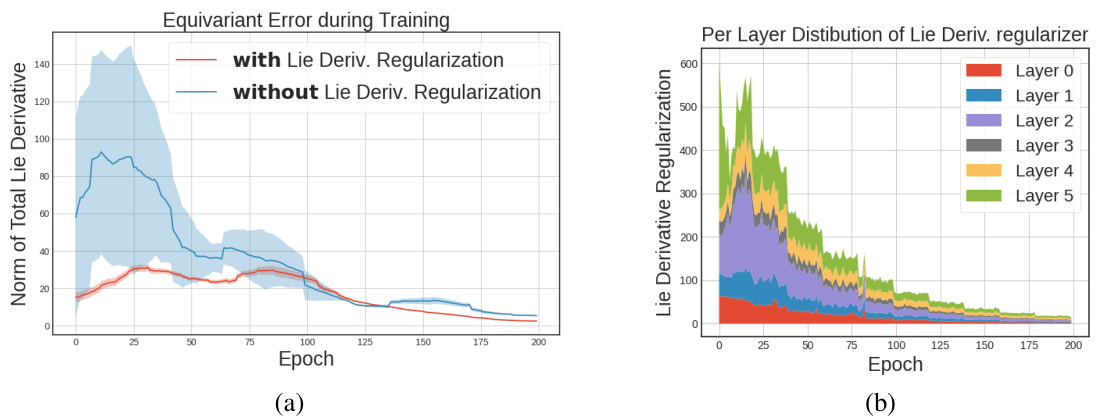
Figure 3 shows two plots. Plot (a) compares the total Lie derivative of the relaxed PointNet model when trained with and without Lie derivative regularization during training. The Lie derivative serves as a measure of the model’s deviation from equivariance. Plot (b) displays the distribution of the Lie derivative regularization term across different layers of the same network during training. The regularization term encourages the model to remain within the equivariant space.

This figure displays the results of experiments evaluating the performance of the proposed optimization framework on the N-body particle simulation task. Two subfigures present the mean average error: (a) shows the relationship between model size (number of message-passing layers) and error, demonstrating that the proposed method achieves lower error across different model sizes. (b) illustrates the impact of dataset size (number of training samples) on error, indicating the proposed method’s consistent performance improvement, even with fewer data points.
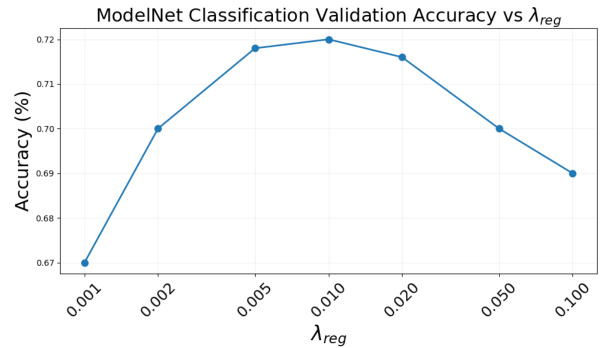
This figure shows the validation accuracy of a VN-PointNet model trained with the proposed method using different values of the regularization parameter (λreg). The experiment used an 80/20 split for training and validation, respectively. The plot demonstrates the impact of λreg on the model’s performance, revealing an optimal value that balances model complexity and generalization.
This figure illustrates the difference between standard training of equivariant neural networks and the proposed training method using constraint relaxation. Standard training restricts the model to a smaller parameter space, potentially hindering optimization. The proposed method relaxes these constraints during training, enabling exploration of a larger hypothesis space containing approximately equivariant models. After training, the model is projected back to the constrained space of equivariant models for testing, leading to improved performance.
More on tables

This table presents the RMSE (Root Mean Squared Error) results for different models on a synthetic smoke plume dataset, evaluating their performance under approximate rotational and scale symmetries. Two evaluation scenarios are considered: ‘Future’, where models are tested on later time steps within the same simulation location as training, and ‘Domain’, where models are evaluated on different spatial locations but the same time steps as training. The models compared include a simple MLP, a convolutional network (Conv), an equivariant convolutional network (Equiv), three approximately equivariant networks (RPP, Lift, RSteer), and the proposed RSteer+Ours method.

This table shows a comparison of the number of parameters and training time per epoch for different models with and without the proposed method. It demonstrates the additional computational cost introduced by the method, showing both the increase in the number of parameters and the small increase in the training time.

The table compares the performance of the proposed optimization framework with two other methods (Equiv-Adapt and Equi-Tuning) and a standard training approach on the ModelNet40 point cloud classification task. The base model used is the VN-PointNet. It highlights that the proposed method achieves comparable results to the best-performing method (Equi-Tuning) which requires significantly more computation during inference.
Full paper#



















