TL;DR#
Current psychological assessment models struggle to balance nomothetic (population-level) and idiographic (individual-level) approaches. Traditional methods either oversimplify by assuming shared traits across individuals or become computationally intractable by modelling each person uniquely. This limitation hinders accurate predictions and personalized interventions.
The researchers address this issue by developing the Idiographic Personality Gaussian Process (IPGP) model. IPGP uses a Gaussian process coregionalization model, adjusted for non-Gaussian ordinal data, to efficiently estimate latent factors. This allows for modeling both shared trait structures and individual deviations. Using real and synthetic data, IPGP demonstrates superior prediction of responses and reveals unique personality clusters compared to benchmark models. This suggests potential improvements in personalized psychological diagnoses and treatment.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in psychology and psychometrics due to its novel approach to personality assessment. It bridges the gap between nomothetic and idiographic approaches, offering a more nuanced and personalized understanding of individual differences. The scalable methodology and promising results open up new avenues for individualized diagnosis and treatment, greatly impacting the fields of mental health and personalized medicine.
Visual Insights#

🔼 This figure illustrates the architecture of the Idiographic Personality Gaussian Process (IPGP) model. The model takes dynamic ordinal data as input, representing responses to multiple survey items across multiple time points for each individual. It uses a multi-task Gaussian process framework to model the latent factors underlying these responses. The model includes both shared (nomothetic) and individual (idiographic) components. The shared component is represented by a population factor loading matrix (Wpop) and covariance matrix (Kpop). The individual component is represented by an individualized loading matrix (Z(i)) and RBF kernel for temporal dynamics (K(i)time). These components are combined to produce a unit-specific covariance matrix, which is then used to infer latent factors (x(t)) that are transformed into the observed ordinal data (y(i)).
read the caption
Figure 1: Proposed IPGP model for inferring latent factors and factor loadings from dynamic ordinal data. Input ordinal observations across indicators are modeled as ordinal transformations of latent dynamic Gaussian processes with individualized RBF kernels and loading matrices.

🔼 This table presents the results of a simulation study comparing the performance of the proposed Idiographic Personality Gaussian Process (IPGP) model against several baseline and ablated models. The metrics used for comparison include training and testing accuracy, log-likelihood, and correlation matrix distance (CMD). The results show that the full IPGP model significantly outperforms all other models, highlighting the importance of its idiographic components and a well-informed population kernel for accurate predictions.
read the caption
Table 1: Comparison of averaged accuracy, log-likelihood and correlation matrix distance between IPGP, baselines, and ablated models in the simulation study. The full IPGP model (indicated in bold) significantly outperforms all ablated and baseline methods. Results from ablations imply that IPGP succeeds in predicting the correct labels due to its idiographic components and proper likelihood, and a well-informed population kernel is crucial in recovering the factor loadings. “—” indicates baseline software that cannot handle missing values.
In-depth insights#
IPGP Framework#
The Idiographic Personality Gaussian Process (IPGP) framework represents a novel approach to psychological assessment, bridging the gap between nomothetic and idiographic methods. It leverages Gaussian process coregionalization to model the complex interrelationships between various psychological traits while simultaneously accommodating individual differences. This allows for the identification of both shared trait structures across a population and unique deviations for individuals, addressing a long-standing debate in psychometrics. The IPGP model’s strength lies in its ability to handle non-Gaussian ordinal data common in psychological surveys, using stochastic variational inference for efficient estimation. Its capacity for dynamic assessment of individualized psychological taxonomies from time-series data provides a powerful tool for longitudinal studies. This innovative approach holds significant potential for personalized diagnosis and treatment, offering more nuanced and accurate insights than traditional methods.
Variational Inference#
Variational inference (VI) is a powerful approximate inference technique, particularly valuable when dealing with complex probability distributions that are intractable to compute exactly. In the context of the provided research, VI is crucial for efficiently estimating the latent factors in the idiographic personality Gaussian process (IPGP) model. This is because the model involves both population-level and individual-specific latent variables, making exact inference computationally prohibitive. VI addresses this by introducing a simpler, tractable distribution (the variational distribution) to approximate the true posterior distribution of the latent variables. The method iteratively optimizes the parameters of this variational distribution to minimize the Kullback-Leibler (KL) divergence between it and the true posterior, effectively approximating the desired latent variable values. The choice of a variational family (e.g., Gaussian) impacts the accuracy and computational efficiency of the approximation. The use of stochastic variational inference further enhances scalability, allowing the method to handle large datasets and more complex model structures that might otherwise be intractable.
Multi-task Learning#
The concept of multi-task learning, as discussed in the research paper, is pivotal to the proposed idiographic personality Gaussian process (IPGP) framework. It leverages the inherent grouped structure of survey batteries, where each battery assesses a specific psychological trait (e.g., a dimension of personality). This grouped structure is cleverly modeled as a multi-task learning problem, enhancing efficiency and capturing correlations between related traits. By considering each survey question as a separate task, while allowing for correlations between tasks, IPGP learns a more comprehensive representation of personality, accommodating both shared traits across individuals and individual deviations. This approach is a significant departure from traditional methods, which often focus on single traits or ignore inter-trait correlations. The multi-task kernel employed is crucial for this, effectively capturing both shared and individual-specific variance components in the latent trait structure. This sophisticated approach allows for more accurate and individualized personality assessment by incorporating both shared and unique aspects of personality, improving both the model’s prediction accuracy and its ability to uncover unique personality taxonomies.
Idiographic Modeling#
Idiographic modeling in psychological research focuses on understanding individuals’ unique characteristics and patterns rather than imposing general population structures. It emphasizes individual differences and context, recognizing that traits and behaviors may manifest differently across individuals. This approach contrasts with nomothetic modeling, which seeks universal laws applicable across the entire population. Key advantages include capturing the nuances of individual experiences and generating more personalized interventions, particularly in clinical settings. However, challenges lie in balancing individualized insights with generalizability and practical application; generating sufficient data for individual models can be resource intensive; and the lack of standardized methods poses a barrier to consistent replication and comparison across studies. Future directions might involve integrating idiographic and nomothetic approaches to harness the strengths of both, exploiting machine learning techniques to tailor models efficiently at scale, and developing standardized measurement tools to improve generalizability and cross-study comparison.
Longitudinal Study#
A longitudinal study design in research offers a powerful way to understand how phenomena evolve over time. In the context of psychological assessment, a longitudinal study using experience sampling methodology (ESM) allows for frequent data collection on individuals’ experiences, providing insights into dynamic psychological processes. Analyzing this data with appropriate statistical models, such as the idiographic personality Gaussian process (IPGP), can reveal individual differences in personality development and how various factors influence these trajectories. This approach moves beyond the limitations of static cross-sectional studies, offering a more nuanced and comprehensive understanding of personality dynamics and paving the way for more individualized approaches to psychological diagnosis and treatment. A well-designed longitudinal study should consider power analysis to ensure sufficient sample size and adequate follow-up periods to capture meaningful changes. Careful consideration of potential biases and limitations of the ESM methodology, such as participant burden and potential reactivity effects, is also necessary for robust data interpretation and valid conclusions.
More visual insights#
More on figures
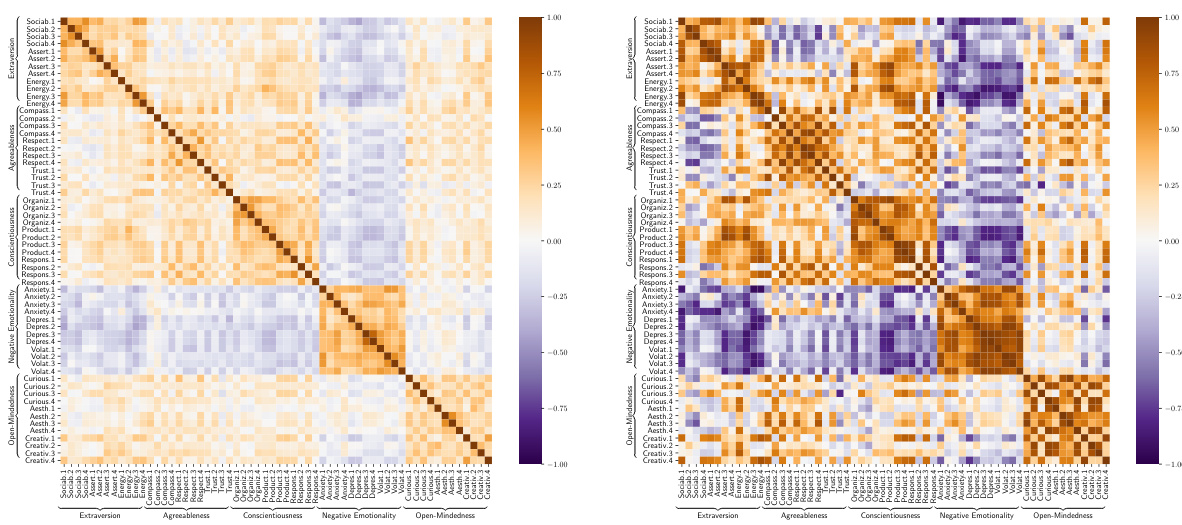
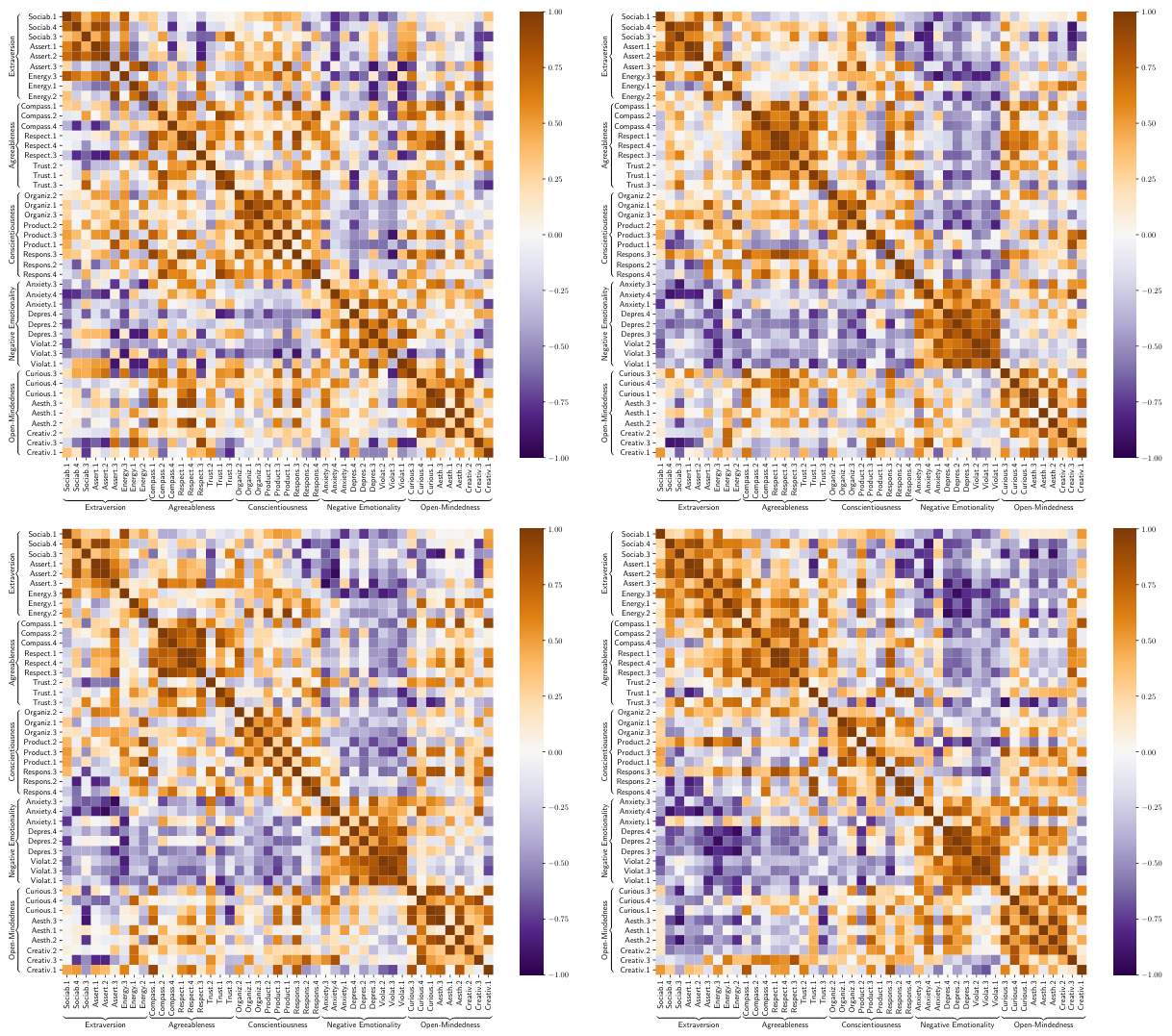
🔼 This figure shows a comparison of two correlation matrices: the raw correlation matrix from the data (left) and the estimated Big Five loading matrix from the IPGP model (right). Both matrices share a block pattern, indicating strong correlations within Big Five personality factors and weak correlations between them. A notable detail is the slight negative correlation observed between questions related to negative emotionality and those related to extraversion and conscientiousness, suggesting the presence of interactions between traits.
read the caption
Figure 2: Illustration of raw correlation matrix (left) and our estimated Big Five loading matrix (right). Both correlation matrices display a block pattern, where estimated interpersonal variation show strong correlation between questions within the same factor of the Big Five personalities and weak correlation across different factors. Besides, questions corresponding negative emotionality show minor negative correlation with those corresponding to extraversion and conscientiousness, suggesting trait-by-trait interaction effects.
🔼 This figure illustrates the architecture of the Idiographic Personality Gaussian Process (IPGP) model. The model takes dynamic ordinal data (e.g., from repeated Likert-scale surveys) as input. It infers latent factors representing underlying personality traits. These latent factors are modeled as dynamic Gaussian processes with individual-specific Radial Basis Function (RBF) kernels, allowing for personalized modeling of trait dynamics. Individualized factor loadings (weights) connect the latent factors to the observed ordinal responses. The model incorporates both population-level shared structure (through population-level factor loadings) and individual-specific deviations (through individualized loadings and kernels).
read the caption
Figure 1: Proposed IPGP model for inferring latent factors and factor loadings from dynamic ordinal data. Input ordinal observations across indicators are modeled as ordinal transformations of latent dynamic Gaussian processes with individualized RBF kernels and loading matrices.
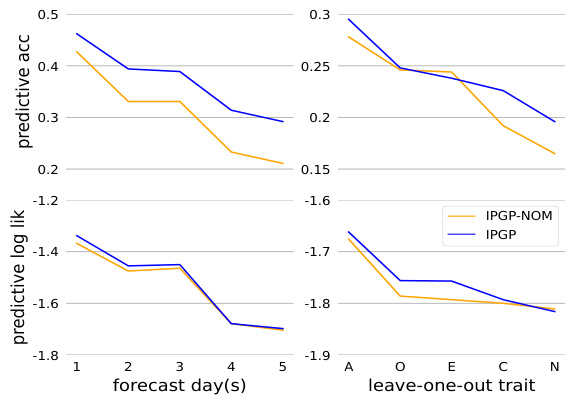
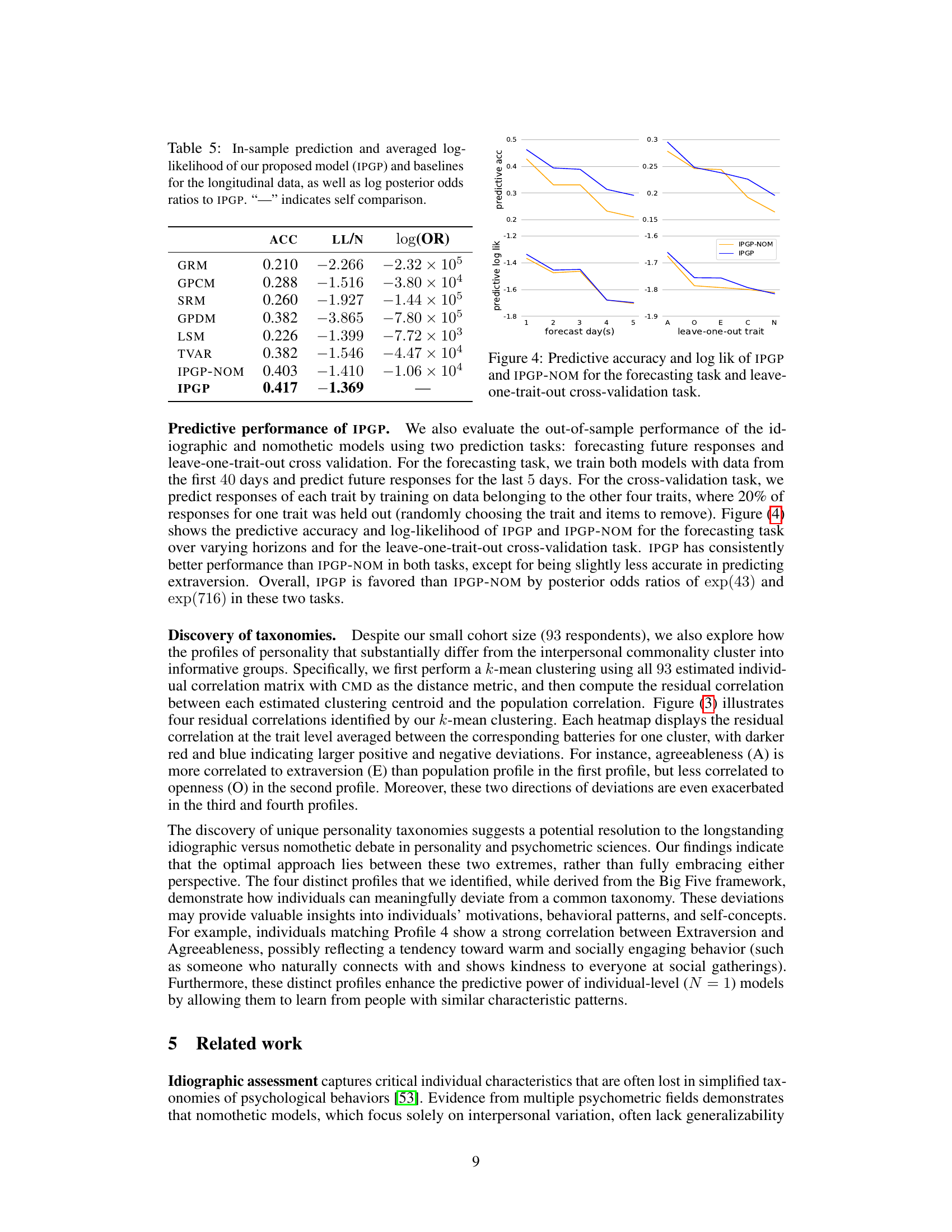
🔼 This figure compares the performance of IPGP (idiographic personality Gaussian process) and IPGP-NOM (a version without idiographic components) on two prediction tasks: forecasting and leave-one-trait-out cross-validation using longitudinal data. The top panels show predictive accuracy for both methods across 5 forecast days and for each of the Big Five personality traits in the leave-one-out task. The bottom panels display the corresponding predictive log-likelihoods for the same tasks. The results highlight IPGP’s superior performance across both prediction tasks and for almost all traits, emphasizing the importance of idiographic components in accurate predictions.
read the caption
Figure 4: Predictive accuracy and log lik of IPGP and IPGP-NOM for the forecasting task and leave-one-trait-out cross-validation task.
🔼 This figure illustrates the architecture of the Idiographic Personality Gaussian Process (IPGP) model. It shows how the model takes ordinal (categorical) data as input, representing responses from a psychological survey given repeatedly over time. The IPGP model uses a multi-task Gaussian process to learn both a common latent structure (shared across individuals) and individual-specific deviations. The model infers latent factors (x(t)) representing underlying personality traits, individualized factor loadings (W(i)), and maps them to the observed ordinal responses (y(i)). The use of RBF (Radial Basis Function) kernels allows for modeling temporal dynamics in personality traits. The model is designed to capture both nomothetic (population-level) and idiographic (individual-level) aspects of personality.
read the caption
Figure 1: Proposed IPGP model for inferring latent factors and factor loadings from dynamic ordinal data. Input ordinal observations across indicators are modeled as ordinal transformations of latent dynamic Gaussian processes with individualized RBF kernels and loading matrices.
More on tables

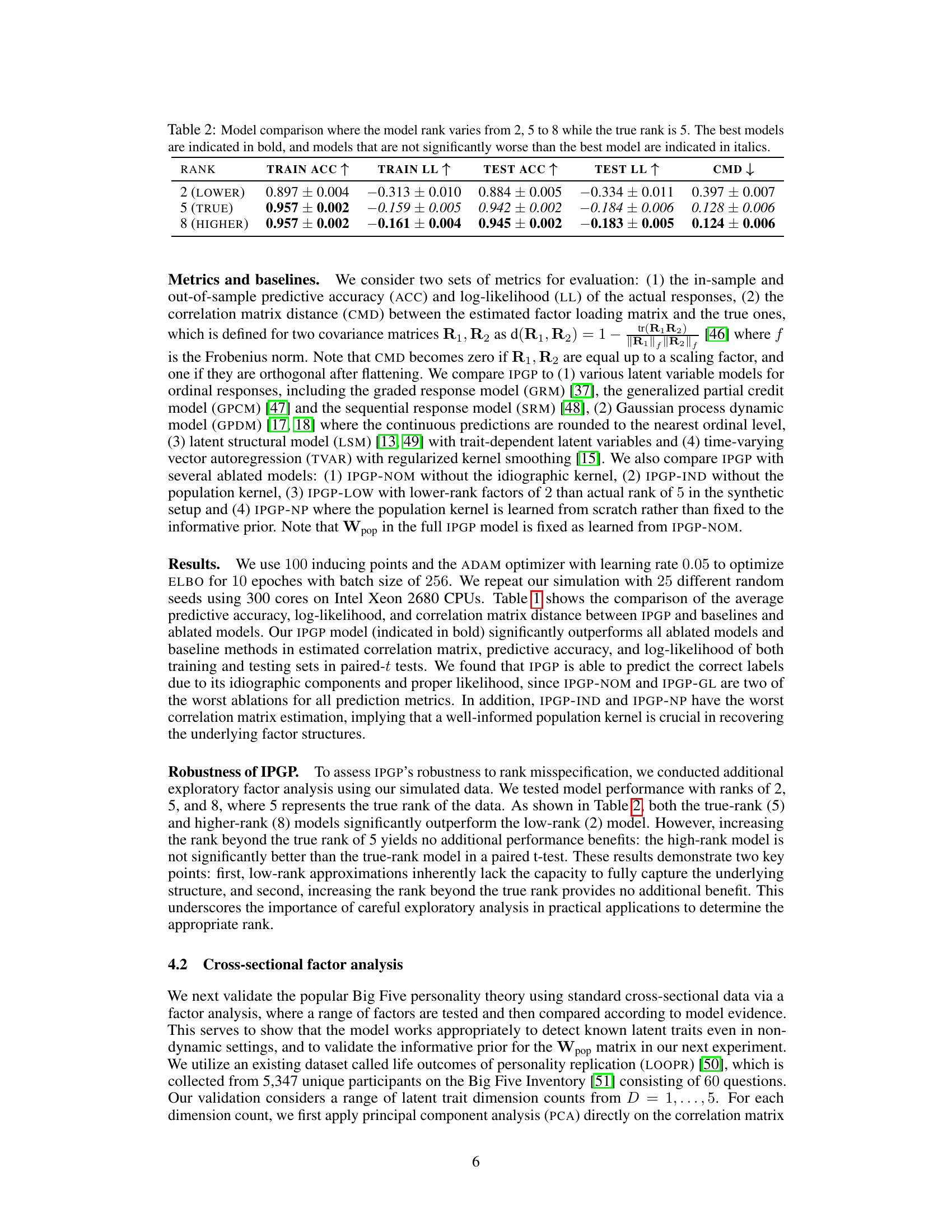
🔼 This table presents the results of a simulation study comparing the performance of the IPGP model with different ranks (2, 5, and 8) against a true rank of 5. The metrics used are training accuracy (TRAIN ACC), training log-likelihood (TRAIN LL), testing accuracy (TEST ACC), testing log-likelihood (TEST LL), and correlation matrix distance (CMD). The best performing model for each rank is highlighted in bold, and models that aren’t statistically significantly worse than the best are italicized. This demonstrates the robustness of IPGP to rank misspecification and shows that the model performs optimally when the rank matches the true rank.
read the caption
Table 2: Model comparison where the model rank varies from 2, 5 to 8 while the true rank is 5. The best models are indicated in bold, and models that are not significantly worse than the best model are indicated in italics.

🔼 This table compares the in-sample accuracy and average log-likelihood of different models (PCA, GRM, GPCM, SRM, GPDM, LSM, and IPGP) when applied to the LOOPR dataset for various latent trait dimensions (D). The best-performing model for each D value is highlighted in bold, and the overall best-performing model across all D values is italicized. It evaluates different models’ performance in capturing the Big Five personality traits.
read the caption
Table 3: In-sample accuracy and averaged log lik of our method and baselines for various ranks D in LOOPR. Best model for each D is indicated in bold and the best model across different Ds is further indicated in italic.

🔼 This table presents the results of an experiment evaluating the performance of the Idiographic Personality Gaussian Process (IPGP) model with varying numbers of latent factors (ranks) on a dataset called LOOPR (Life Outcomes of Personality Replication). The table shows the log-likelihood per data point (LL/N) and the Bayesian Information Criterion (BIC) for IPGP models trained with ranks from 1 to 10. Lower BIC values indicate better model fit, suggesting an optimal rank that balances model complexity and goodness of fit.
read the caption
Table 4: Model performance of IPGP with model ranks from 1 to 10 in LOOPR data.
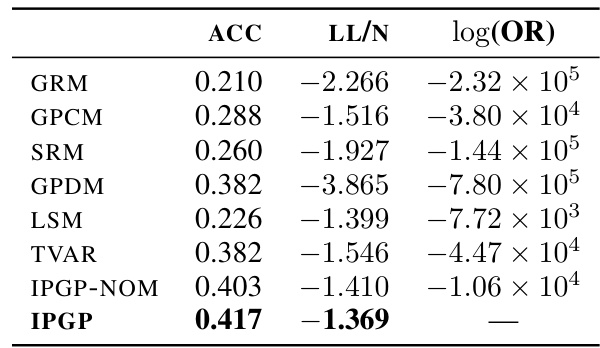
🔼 This table presents the in-sample predictive accuracy (ACC) and average log-likelihood (LL/N) for various models applied to longitudinal data. It compares the idiographic personality Gaussian process (IPGP) model to several baselines (GRM, GPCM, SRM, GPDM, LSM, TVAR, and IPGP-NOM). The log posterior odds ratio (log(OR)) is also provided, showing the relative support for IPGP compared to each baseline model. A higher ACC and LL/N, and a higher log(OR) relative to baselines indicate better model performance. The ‘-’ indicates that no comparison is made against the IPGP model itself.
read the caption
Table 5: In-sample prediction and averaged log-likelihood of our proposed model (IPGP) and baselines for the longitudinal data, as well as log posterior odds ratios to IPGP. '-' indicates self comparison.
🔼 This table presents a comparison of the performance of the Idiographic Personality Gaussian Process (IPGP) model against several baseline and ablated models in a simulation study. The metrics used are prediction accuracy, log-likelihood, and a correlation matrix distance measure. The results show that IPGP significantly outperforms the other methods, highlighting the importance of its idiographic components and the use of a well-informed population kernel.
read the caption
Table 1: Comparison of averaged accuracy, log-likelihood and correlation matrix distance between IPGP, baselines, and ablated models in the simulation study. The full IPGP model (indicated in bold) significantly outperforms all ablated and baseline methods. Results from ablations imply that IPGP succeeds in predicting the correct labels due to its idiographic components and proper likelihood, and a well-informed population kernel is crucial in recovering the factor loadings. “—” indicates baseline software that cannot handle missing values.
Full paper#