TL;DR#
Traditional image steganography relies on heuristic methods for cover image selection, often leading to suboptimal message hiding and reduced image quality. The relationship between image complexity metrics and message hiding efficacy is unclear. Existing techniques often involve exhaustive searches through large image databases, a computationally expensive approach. This makes traditional cover selection methods inefficient and potentially ineffective for modern steganographic applications.
This research proposes a novel cover selection framework that addresses these shortcomings. The proposed method optimizes within the latent space of pre-trained generative models (like DDIM or GANs) to identify cover images ideal for message hiding. This approach significantly improves message recovery rates and image quality. The study also reveals that effective message hiding predominantly occurs in low-variance image pixels, mirroring the waterfilling algorithm in parallel Gaussian channels. This framework is demonstrated using multiple public datasets, showcasing improved performance over existing methods. The researchers further evaluate the robustness of their method against common attacks, demonstrating effectiveness in various scenarios.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel approach to cover selection in image steganography, significantly improving message recovery and image quality. It leverages advancements in generative models, offering a substantial improvement over traditional methods. This work opens new avenues for research in optimizing generative models for steganography and enhancing security in image-based communication. The information-theoretic analysis linking low-variance pixels to message embedding enhances theoretical understanding of steganography, providing a foundation for further advancements in this field.
Visual Insights#

🔼 This figure illustrates the image steganography framework. The left panel shows a basic encoder-decoder structure where a secret message (m) is embedded into a cover image (x) to produce a steganographic image (s). The right panel showcases example images from ImageNet. It compares randomly selected images with their optimized versions after undergoing the proposed cover selection framework. The optimized images achieve significantly lower message recovery errors (||m - m||) while maintaining high visual quality.
read the caption
Figure 1: Left: Image steganography framework: the encoder takes as input the cover image x and a secret binary message m and outputs the steganographic image s. The decoder then estimates m from s. Right: Randomly sampled cover images from the ImageNet dataset before and after optimization using our framework (described in Section 3). These optimized images demonstrate a significantly reduced error ||m – m|| while maintaining high image quality.
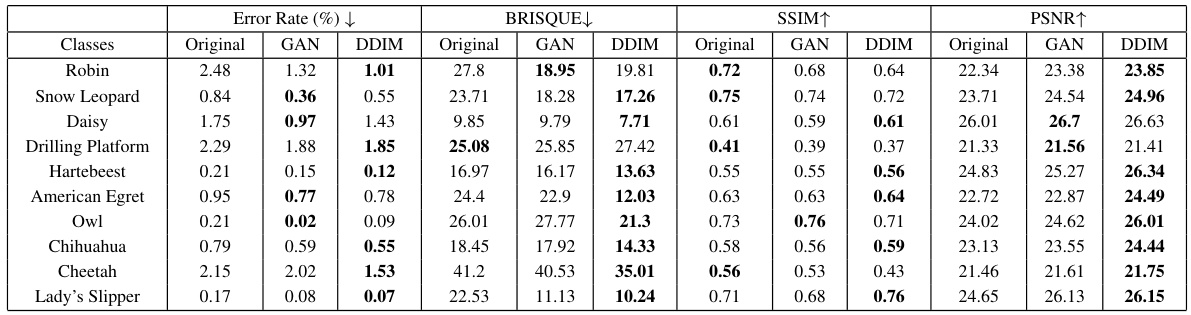
🔼 This table compares the performance of GAN-based and DDIM-based cover selection methods on the ImageNet dataset using a payload of 4 bits per pixel. It shows the error rate, BRISQUE score (image quality), SSIM (structural similarity), and PSNR (peak signal-to-noise ratio) for original images and images optimized using both GAN and DDIM methods. The results demonstrate the superior performance of DDIM in reducing error rates while maintaining or improving image quality.
read the caption
Table 1: Comparative performance of GAN-based and DDIM-based cover selection techniques on the ImageNet dataset, with a payload B = 4 bpp. DDIM-optimized images achieve a significant gain over the original images and GAN-optimized images in both error rate reduction and image quality.
In-depth insights#
Neural Cover Selection#
The concept of “Neural Cover Selection” introduces a novel approach to image steganography. Traditional methods rely on heuristic metrics, often failing to directly correlate with message hiding efficacy. This neural approach leverages the power of pre-trained generative models to optimize cover image selection within the latent space. By minimizing message recovery errors while maintaining visual integrity, it surpasses the limitations of exhaustive searches. The key innovation lies in framing cover selection as an optimization problem, which is solved using gradient-based methods to adjust latent vectors, ultimately generating images ideal for embedding messages. This method demonstrates significant advantages in message recovery and image quality, offering a more effective and efficient way to conceal information within digital images. Further analysis reveals a surprising parallel to the waterfilling algorithm, suggesting that message hiding primarily takes place in low-variance pixels, and the optimization process itself enhances the prevalence of such pixels. This novel approach presents a substantial advancement in the field of steganography, moving beyond simple heuristic evaluation toward a data-driven, optimized solution.
DDIM-based Optimization#
The DDIM-based optimization strategy presented in this research paper is a novel approach to cover selection in image steganography. It leverages the power of pretrained denoising diffusion implicit models (DDIMs) to refine the latent representation of a cover image, aiming for optimal message embedding. The core innovation is the integration of a message recovery loss function within the DDIM’s iterative refinement process. This loss function guides the optimization towards cover images that minimize the error in message extraction while maintaining image quality. The method’s strength lies in its ability to generate tailored cover images rather than selecting from a predefined dataset, thus overcoming limitations of traditional methods. This optimization shows promising results in significantly reducing error rates and improving image quality metrics. While the information-theoretic analysis suggests an alignment with the waterfilling algorithm, further investigation is needed to fully explore the relationship between latent space optimization, low-variance pixel manipulation, and message embedding efficacy. The framework exhibits its robustness by extending its application to different image datasets and demonstrating its resilience against JPEG compression. However, performance variations are observed across different payload capacities and there’s room for enhancement in addressing image quality constraints at lower bpp levels.
Waterfilling Analogy#
The waterfilling analogy in the paper provides a compelling theoretical framework for understanding the observed behavior of the neural steganographic encoder. The core idea is that the encoder preferentially hides messages in low-variance pixels, mirroring the optimal power allocation strategy in parallel Gaussian channels. This waterfilling analogy is significant as it shows that the seemingly heuristic embedding strategy implicitly used by the encoder is, in fact, aligned with a well-established information-theoretic principle. This unexpected connection between neural networks and communication theory provides a deeper understanding of the efficacy of the cover selection optimization. The observation that the optimization increases the number of low-variance pixels further supports this analogy, demonstrating that the method leverages the inherent properties of the communication channel. The study quantifies the correlation between low-variance pixels and message embedding, validating the waterfilling analogy and adding to the understanding of neural steganography. This theoretical grounding is crucial in moving beyond mere empirical observation and provides a robust foundation for future work in improving neural steganography methods.
Steganography Analysis#
A robust steganography system necessitates a thorough analysis of its resilience against detection. Steganography analysis would involve evaluating the system’s ability to embed messages imperceptibly within cover images, while simultaneously resisting detection by steganalysis techniques. This requires testing under various conditions, including different payload sizes, cover image types, and the application of diverse steganalysis methods. The analysis should also evaluate the trade-off between embedding capacity and imperceptibility. A crucial aspect of this analysis involves examining the distribution of modifications made to the cover image. If modifications are uniformly distributed, the system may be more easily detected. Therefore, a well-designed steganography system seeks to exploit inherent characteristics of the cover images to minimize detectability. Finally, the analysis should consider the computational complexity, both in embedding and detection, to assess the practicality of the proposed method. Benchmarking against existing steganography techniques is essential to demonstrate the system’s competitive advantage in terms of both capacity and security.
Future Research#
The paper’s core contribution is a novel cover selection framework for image steganography, leveraging pretrained generative models. Future research could explore extending this framework to handle correlated Gaussian channels, moving beyond the independent channel assumption of the current work. Investigating various regularization techniques to maintain high image quality at lower bit rates (bpp) is another key area. Exploring the interplay between different generative models and steganographic encoder-decoder pairs would be valuable to see how performance varies, especially under constraints such as JPEG compression or adversarial attacks. A deeper investigation into the encoder’s behavior, potentially uncovering more nuanced embedding strategies, is also necessary. Finally, because the success of steganography is linked to the ability to evade detection, rigorous testing against state-of-the-art steganalysis techniques with various payload sizes and image types is vital. This includes adapting the framework for more robust security against different types of image manipulations and noise.
More visual insights#
More on figures

🔼 This figure shows a schematic of the proposed DDIM-based cover selection framework. The framework starts with an input cover image (x0) that undergoes a forward diffusion process to generate a latent representation (xT). This latent representation is then optimized to minimize the message recovery error, and the optimized latent vector is used in a reverse diffusion process to reconstruct a refined cover image. This refined image is then processed by a pretrained steganographic encoder-decoder pair, and the resulting message recovery error is fed back into the optimization process. The process leverages pretrained models for both the DDIM and the encoder-decoder.
read the caption
Figure 2: DDIM-based cover selection framework overview. The input cover image x0 is first converted to the latent space xT via forward diffusion. Then, guided the message recovery loss, the latent space is fine-tuned, and the updated cover image is generated via the reverse diffusion process. The DDIM model as well as the steganographic encoder-decoder pair are pretrained.
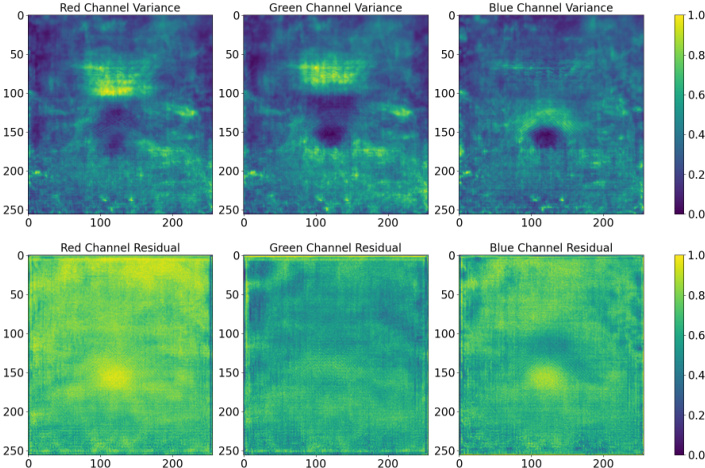
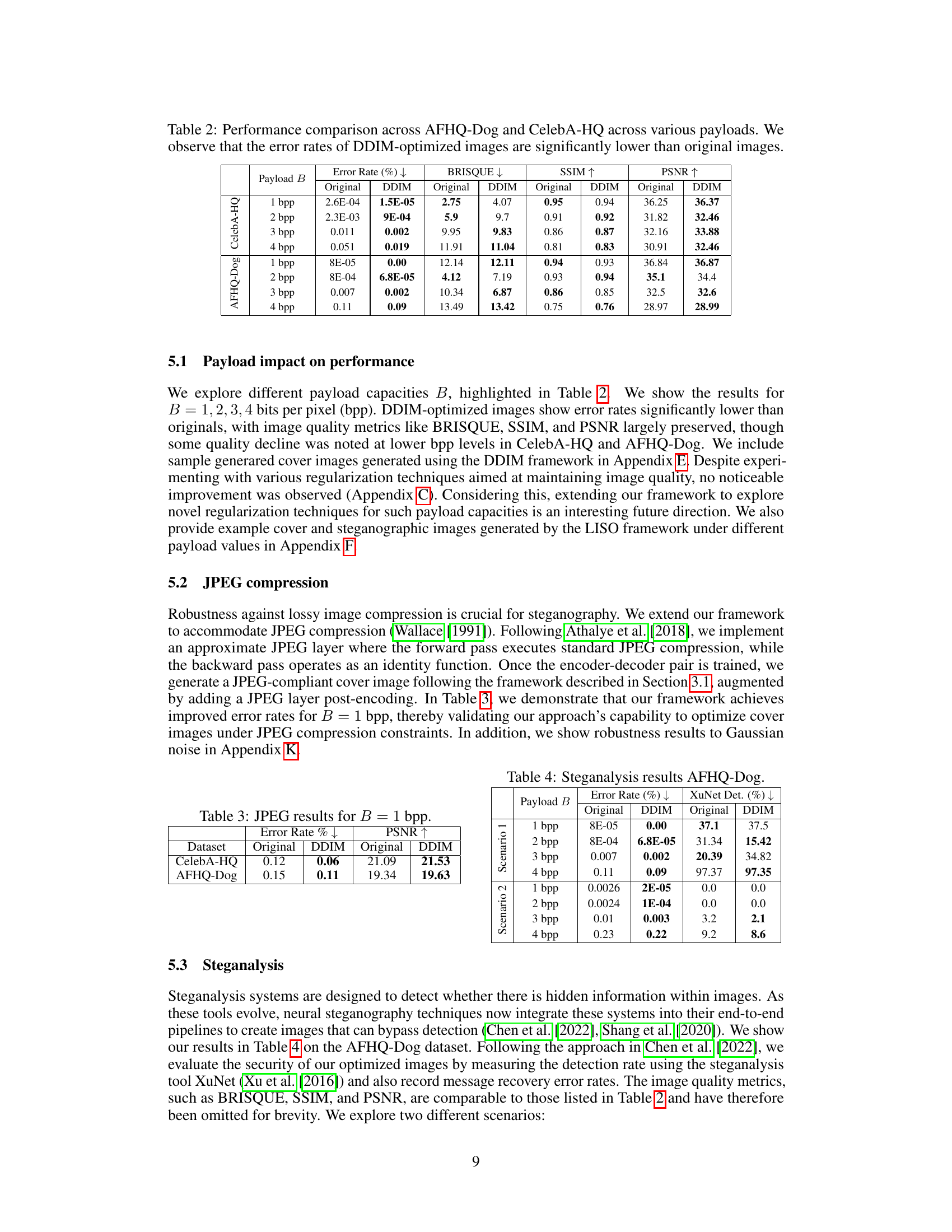
🔼 This figure visualizes the pixel-wise variances and residuals in three color channels (Red, Green, Blue) for a batch of 500 Robin images. The top row displays heatmaps representing the normalized variance of each pixel across the image batch, indicating the variability of pixel intensity. The bottom row shows heatmaps of the absolute residuals (differences) between the original cover image and the steganographic image produced by the encoder, after the secret message has been embedded. The comparison helps demonstrate the correlation between low-variance pixels and the locations where the message is predominantly hidden by the encoder. It supports the paper’s claim that message embedding mainly occurs in low-variance pixels, a characteristic similar to the waterfilling algorithm.
read the caption
Figure 3: Normalized pixel variances (top) and residuals (bottom) calculated across a batch of 500 Robin images for each color channel, before optimization.

🔼 This figure shows the results of applying the waterfilling algorithm to the variance of each color channel (red, green, blue) across 500 Robin images from the ImageNet dataset. The waterfilling algorithm is an optimal power allocation strategy for parallel Gaussian channels, assigning higher power to channels with lower variance to maximize the capacity for reliable transmission of information. The resulting heatmaps illustrate the calculated power coefficients (Yi) for each pixel in each color channel, indicating where higher power would be allocated according to the waterfilling principle. Areas with darker shades represent higher power coefficients, suggesting that these regions (low-variance pixels) are optimal for embedding information. This visual representation directly relates to the paper’s claim that their neural steganographic encoder embeds information into low variance pixels.
read the caption
Figure 4: Power coefficients Yi for each color channel, calculated using a batch of 500 Robin images.

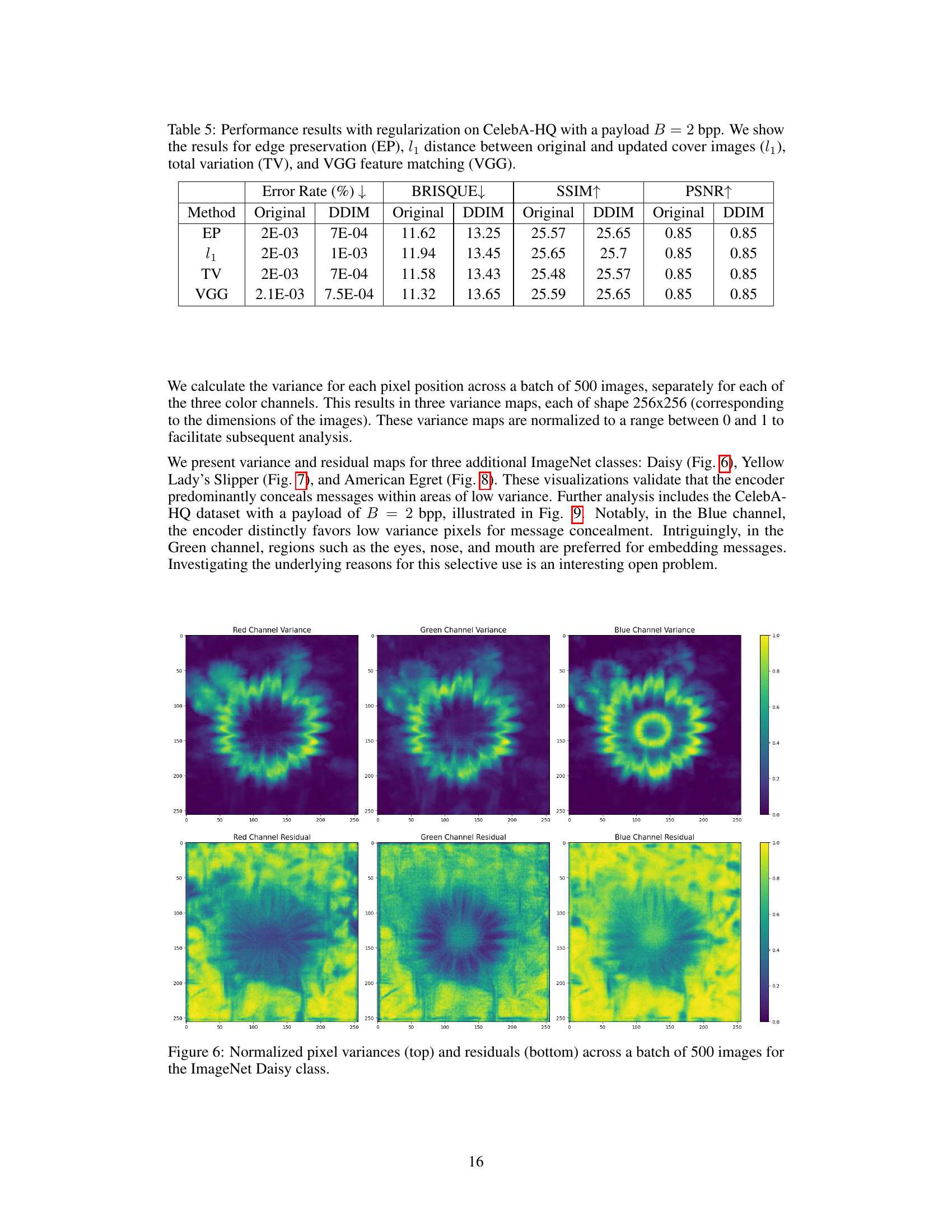
🔼 This figure shows the normalized pixel variances and residuals for a batch of 500 ‘Robin’ images from the ImageNet dataset. The top row displays heatmaps representing the variance of each pixel across the red, green, and blue color channels. The bottom row shows corresponding heatmaps of the residuals obtained after applying a pretrained steganographic encoder. The comparison illustrates the correlation between low-variance pixels and the locations where the encoder predominantly embeds messages, supporting the paper’s hypothesis about the encoder’s strategy of utilizing low-variance pixels for concealing data.
read the caption
Figure 3: Normalized pixel variances (top) and residuals (bottom) calculated across a batch of 500 Robin images for each color channel, before optimization.
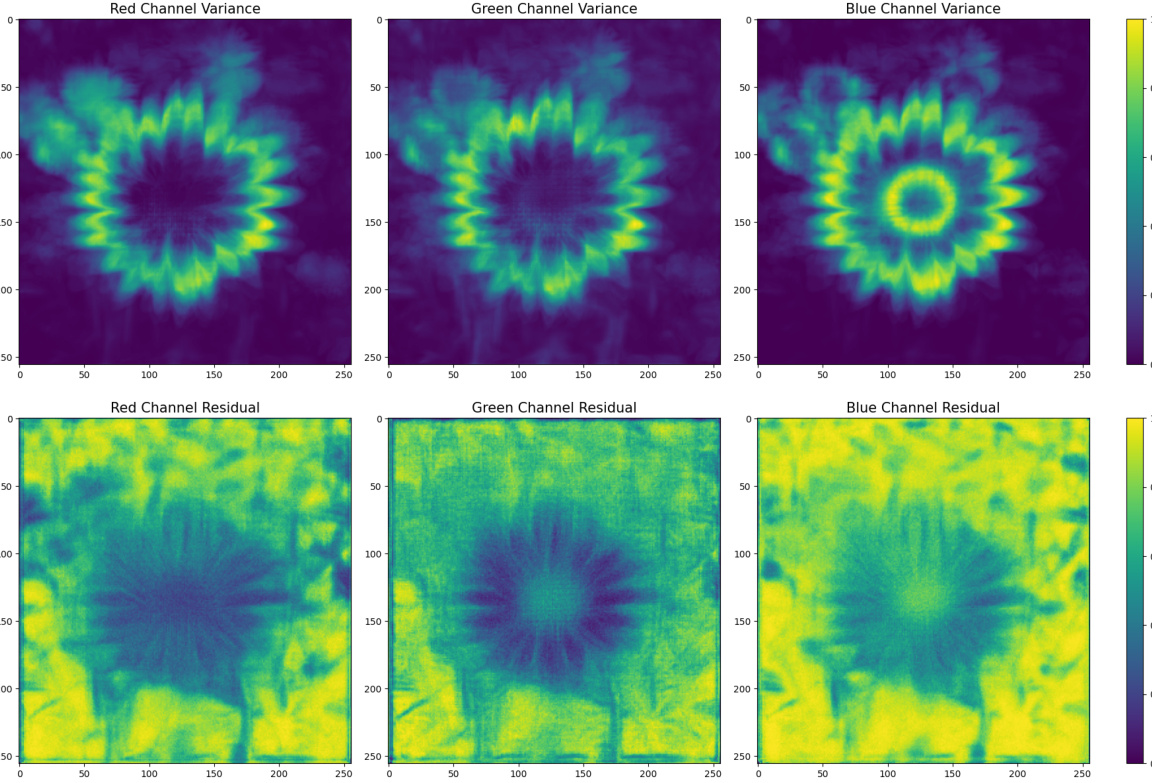
🔼 This figure displays the normalized pixel variances and residuals for the red, green, and blue channels of 500 Robin images from the ImageNet dataset. The top row shows heatmaps representing the variance of pixel intensities in each channel. The bottom row displays heatmaps illustrating the residuals after applying a steganographic encoder to the images. The aim is to visually demonstrate the correlation between low-variance pixels and the locations where the steganographic encoder primarily embeds secret messages. Brighter colors indicate higher variance/residuals; darker colors represent lower values.
read the caption
Figure 3: Normalized pixel variances (top) and residuals (bottom) calculated across a batch of 500 Robin images for each color channel, before optimization.
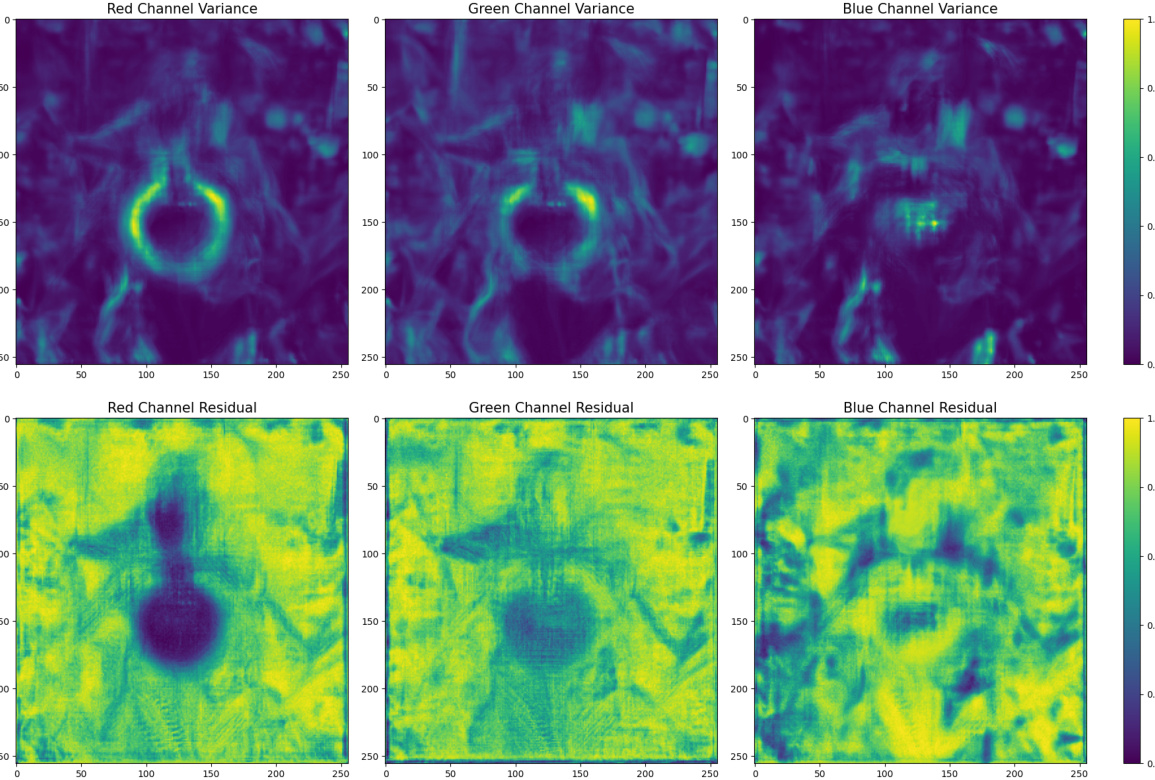
🔼 This figure visualizes the variances (top) and residuals (bottom) of pixel intensities across three color channels (Red, Green, Blue) for 500 Robin images from the ImageNet dataset. The top row shows heatmaps representing the variance of each pixel. Higher variance indicates greater variation in intensity within the pixel across all 500 images; lower values mean consistent intensity. The bottom row shows heatmaps of the residuals after applying a steganographic encoder. The residuals represent the absolute differences between original cover images and their steganographic counterparts. A high residual means a large change in the pixel intensity during the encoding process. The figure aims to demonstrate a correlation between low-variance pixels and high-magnitude residuals, suggesting that the steganographic encoder preferentially modifies pixels with low variance to embed the secret message.
read the caption
Figure 3: Normalized pixel variances (top) and residuals (bottom) calculated across a batch of 500 Robin images for each color channel, before optimization.

🔼 This figure visualizes the variance and residuals of pixel values for the red, green, and blue channels of a batch of 500 Robin images before any optimization is applied. The top row shows heatmaps representing the normalized pixel variances, indicating the variability of pixel intensity across the image. The bottom row shows heatmaps of the residuals, which represent the absolute difference between the original image and a steganographic version of the image after a message is embedded. The correlation between variance and residual magnitude suggests that the steganographic encoder preferentially modifies pixels with low variance, suggesting the effectiveness of targeting low-variance pixels for message embedding.
read the caption
Figure 3: Normalized pixel variances (top) and residuals (bottom) calculated across a batch of 500 Robin images for each color channel, before optimization.

🔼 This figure visualizes the pixel-wise variance and residuals for a batch of 500 Robin images from the ImageNet dataset. The top row shows heatmaps representing the normalized variance for each color channel (red, green, blue). The bottom row shows heatmaps of the residuals, calculated as the absolute difference between the original cover images and their steganographic counterparts. The figure illustrates a strong correlation between low variance pixels and larger residual magnitudes, suggesting that the neural steganographic encoder preferentially hides messages in low-variance regions of the image.
read the caption
Figure 3: Normalized pixel variances (top) and residuals (bottom) calculated across a batch of 500 Robin images for each color channel, before optimization.

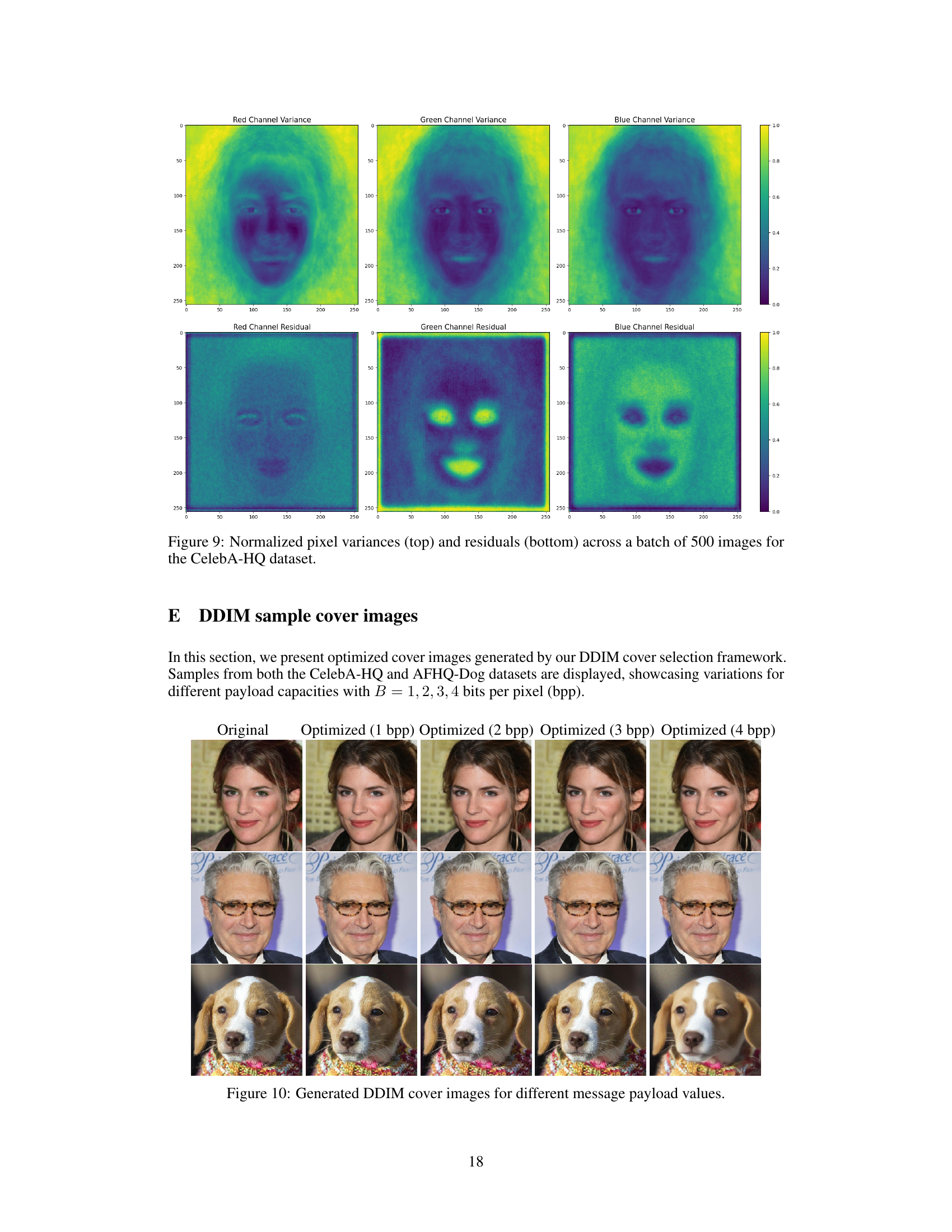
🔼 This figure shows example images generated using the DDIM-based cover selection framework. It displays original images and their optimized counterparts for varying payload sizes (1, 2, 3, and 4 bits per pixel). The images are from the CelebA-HQ and AFHQ-Dog datasets, showcasing how the optimization impacts image quality at different bit rates.
read the caption
Figure 10: Generated DDIM cover images for different message payload values.

🔼 This figure shows four pairs of cover images and their corresponding steganographic images generated using the LISO steganography framework at different bit rates (1, 2, 3, and 4 bits per pixel). The images are from the CelebA-HQ and AFHQ datasets. The purpose of this figure is to visually demonstrate the effectiveness of the LISO framework in embedding secret messages into cover images while maintaining visual similarity.
read the caption
Figure 11: Covers and their corresponding steganographic images.

🔼 This figure compares the results of generating steganographic images using both GAN and DDIM methods. It shows that the DDIM method preserves the semantic meaning and structure of the images better than the GAN method. While both methods produce images that are visually similar to the original covers, the GAN method tends to alter the images more significantly, sometimes affecting the semantic meaning of the original image.
read the caption
Figure 12: Generated steganographic images: GAN vs DDIM.
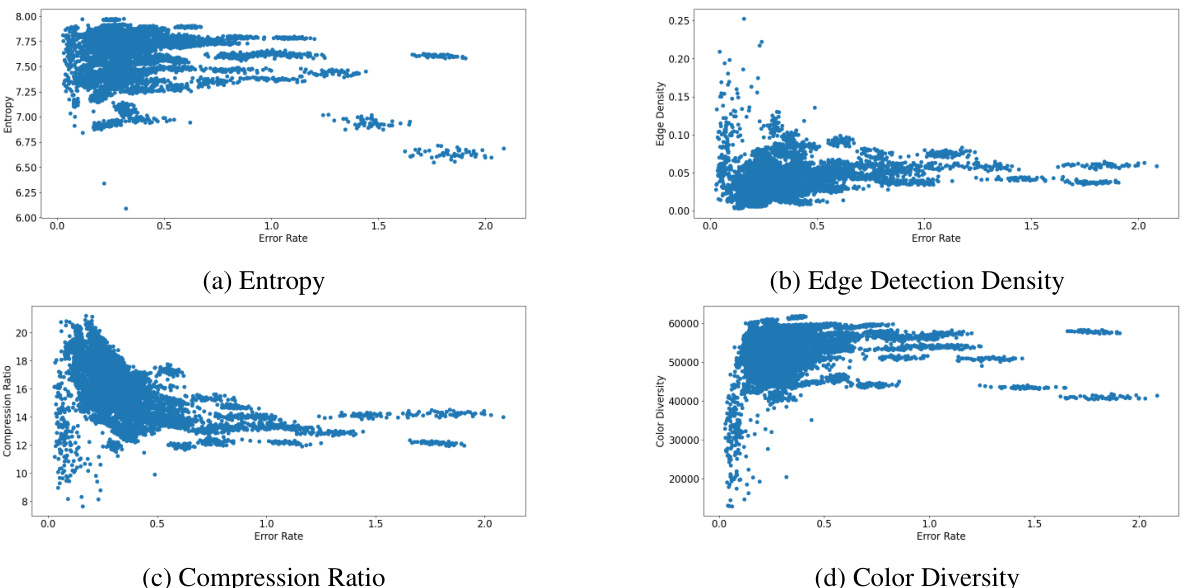
🔼 This figure shows the correlation between image complexity metrics (entropy, edge detection density, compression ratio, and color diversity) and the error rate of the steganographic process. Each subplot shows a scatter plot with one complexity metric on the y-axis and error rate on the x-axis. The plots visualize how these complexity metrics relate to the success of the steganographic process, revealing insights into which image characteristics influence the effectiveness of hiding messages.
read the caption
Figure 13: Image complexity metrics vs error rate

🔼 The figure illustrates the image steganography framework where an encoder takes a cover image and a secret message as input, outputs a steganographic image, and a decoder recovers the message. It also shows the results of cover image optimization using the proposed framework. Optimized images significantly reduce the error between original and recovered messages while maintaining high image quality.
read the caption
Figure 1: Left: Image steganography framework: the encoder takes as input the cover image x and a secret binary message m and outputs the steganographic image s. The decoder then estimates m from s. Right: Randomly sampled cover images from the ImageNet dataset before and after optimization using our framework (described in Section 3). These optimized images demonstrate a significantly reduced error ||m – m|| while maintaining high image quality.
More on tables
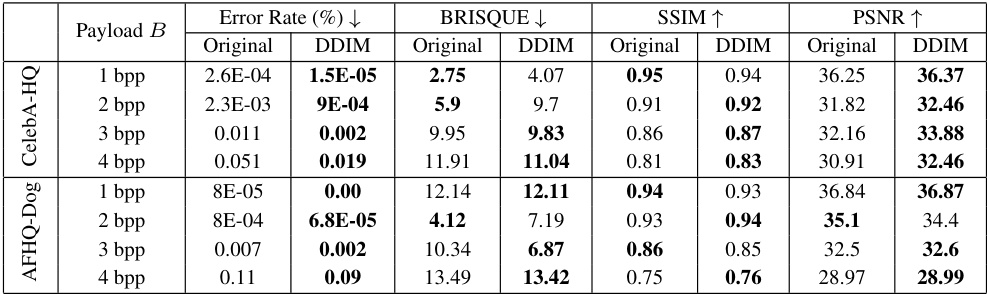
🔼 This table compares the performance of GAN-based and DDIM-based cover selection methods on the ImageNet dataset using a payload of 4 bits per pixel (bpp). The results show error rates (%), BRISQUE scores (lower is better), SSIM scores (higher is better), and PSNR scores (higher is better) for original images and images optimized using both GAN and DDIM methods. The table highlights the significant improvement in error rate and image quality achieved by the DDIM-optimized images compared to the original and GAN-optimized images.
read the caption
Table 1: Comparative performance of GAN-based and DDIM-based cover selection techniques on the ImageNet dataset, with a payload B = 4 bpp. DDIM-optimized images achieve a significant gain over the original images and GAN-optimized images in both error rate reduction and image quality.
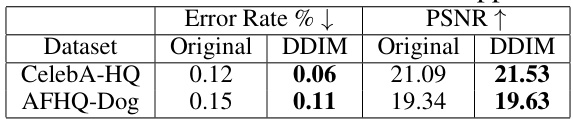
🔼 This table presents the results of applying the proposed framework with a payload of 1 bit per pixel (bpp) to images that have undergone JPEG compression. It shows a comparison of the error rate and PSNR between the original images and the images optimized using the DDIM-based cover selection method. The results demonstrate the effectiveness of the approach in generating images with lower error rates and comparable image quality even after JPEG compression.
read the caption
Table 3: JPEG results for B = 1 bpp.

🔼 This table compares the performance of GAN-based and DDIM-based cover selection methods on the ImageNet dataset using a payload of 4 bits per pixel (bpp). For several image classes, it shows the error rate (percentage of incorrect message bits recovered), BRISQUE score (measuring perceived image quality), SSIM (structural similarity index), and PSNR (peak signal-to-noise ratio) for original, GAN-optimized, and DDIM-optimized images. The results demonstrate that the DDIM-optimized images significantly reduce the error rate and maintain or improve image quality.
read the caption
Table 1: Comparative performance of GAN-based and DDIM-based cover selection techniques on the ImageNet dataset, with a payload B = 4 bpp. DDIM-optimized images achieve a significant gain over the original images and GAN-optimized images in both error rate reduction and image quality.

🔼 This table compares the performance of GAN-based and DDIM-based cover selection methods on the ImageNet dataset using a payload of 4 bits per pixel (bpp). It shows the error rate, BRISQUE score (image quality), SSIM (structural similarity), and PSNR (peak signal-to-noise ratio) for original images and those optimized using GANs and DDIMs. The results demonstrate that DDIM-optimized images significantly reduce the error rate while maintaining or improving image quality compared to original and GAN-optimized images.
read the caption
Table 1: Comparative performance of GAN-based and DDIM-based cover selection techniques on the ImageNet dataset, with a payload B = 4 bpp. DDIM-optimized images achieve a significant gain over the original images and GAN-optimized images in both error rate reduction and image quality.

🔼 This table presents the performance results of different regularization methods applied during the cover selection process using the CelebA-HQ dataset with a payload of 2 bits per pixel (bpp). The methods evaluated include edge preservation (EP), L1 distance between original and updated cover images (l1), total variation (TV), and VGG feature matching (VGG). For each method, the table shows the error rate, BRISQUE score, SSIM, and PSNR. The results demonstrate that the various regularization techniques did not significantly enhance the performance.
read the caption
Table 5: Performance results with regularization on CelebA-HQ with a payload B = 2 bpp. We show the resuls for edge preservation (EP), l₁ distance between original and updated cover images (l1), total variation (TV), and VGG feature matching (VGG).
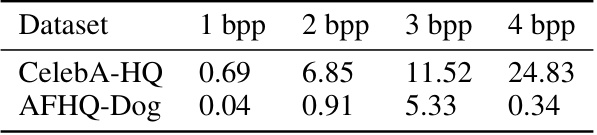
🔼 This table shows the average computation time required for the DDIM-based cover selection method, measured in seconds, for different payload values (bits per pixel). The results are categorized by dataset: CelebA-HQ and AFHQ-Dog. This provides insights into the computational cost of the optimization process at different data sizes.
read the caption
Table 6: Average computation time of DDIM-based cover selection (in seconds) for different payload values.

🔼 This table compares the performance of GAN-based and DDIM-based cover selection methods on the ImageNet dataset using a payload of 4 bits per pixel (bpp). The results show error rates, BRISQUE scores, SSIM (Structural Similarity Index), and PSNR (Peak Signal-to-Noise Ratio) values for original images and images optimized using each method. It highlights the superior performance of DDIM in both reducing error rates and improving image quality.
read the caption
Table 1: Comparative performance of GAN-based and DDIM-based cover selection techniques on the ImageNet dataset, with a payload B = 4 bpp. DDIM-optimized images achieve a significant gain over the original images and GAN-optimized images in both error rate reduction and image quality.

🔼 This table presents the results of evaluating the robustness of the DDIM-based cover selection approach to Gaussian noise. The experiment used a payload of 4 bits per pixel (bpp) on the CelebA-HQ dataset. Different levels of Gaussian noise (variance β) were introduced into the steganographic image before decoding. The table shows the effect of the noise on the error rate, BRISQUE (image quality), SSIM (structural similarity), and PSNR (peak signal-to-noise ratio). Lower values for error rate, BRISQUE, and higher values for SSIM and PSNR indicate better robustness to noise.
read the caption
Table 8: Robustness to Gaussian noise for a payload B = 4 bpp on CelebA-HQ.
Full paper#