↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep neural networks (DNNs) are vulnerable to adversarial attacks, and existing defenses often struggle with multiple attack types. The paper identifies a key tradeoff between robustness against multiple attacks and model accuracy, which makes achieving high “union accuracy” (robustness across all attacks) particularly difficult. Prior methods like average-case and worst-case adversarial training have limitations regarding accuracy or computational cost.
The authors introduce RAMP, a novel training framework. RAMP uses a logit pairing loss that enforces similar predictions for different attack types. Moreover, it bridges natural training and adversarial training through gradient projection to improve both accuracy and robustness. Experiments show RAMP achieves higher union accuracy and superior generalization against a range of adversarial attacks and natural corruptions on various datasets such as CIFAR-10 and ImageNet. RAMP shows promise in creating more robust and resilient DNNs for real-world applications.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the critical challenge of improving the robustness of deep neural networks (DNNs) against multiple adversarial attacks which is a major limitation of current DNNs. The proposed method, RAMP, offers a novel approach that outperforms existing techniques, thereby paving the way for more secure and reliable DNN applications. The theoretical analysis further enhances its significance by providing insights that guide future research in adversarial robustness and DNN security.
Visual Insights#
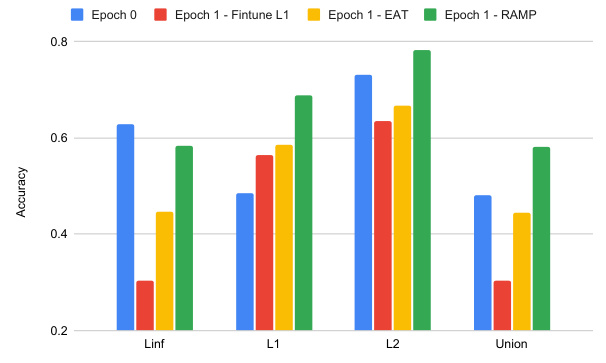
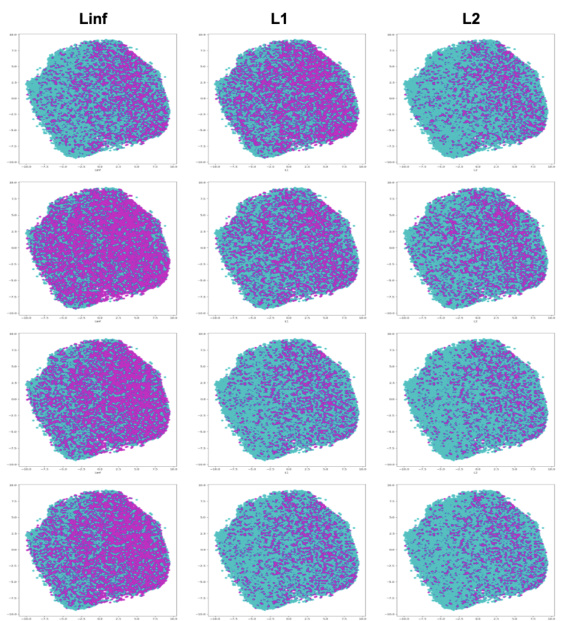
This figure visualizes the changes in l1, l2, l∞, and union robustness when fine-tuning a pre-trained l∞-adversarial training (AT) model with l1 examples. It compares the robustness after one epoch of fine-tuning using three different methods: l1 fine-tuning, Extreme Adversarial Training (EAT), and the proposed RAMP method. The results show that l1 fine-tuning and EAT lead to a substantial decrease in l∞ robustness, while RAMP effectively maintains both l∞ and union robustness.

This table presents the results of experiments comparing RAMP’s performance against E-AT and MAX under different epsilon values for both training from scratch and robust fine-tuning scenarios. It demonstrates RAMP’s consistent superior performance across various settings by showing its higher union accuracy and superior robustness in handling diverse perturbation types.
In-depth insights#
Multi-norm Robustness#
The concept of “multi-norm robustness” in adversarial machine learning addresses the limitation of models trained to be robust against only a single type of perturbation (e.g., l∞, l1, or l2). Real-world adversarial attacks are unlikely to be constrained by a single norm, so a model robust to one norm may be vulnerable to others. Multi-norm robustness aims to build models that are resilient across multiple perturbation types, significantly improving their real-world robustness. Achieving this is challenging due to the trade-offs between robustness against different norms and overall accuracy. The core challenge lies in finding training strategies that effectively balance these trade-offs, potentially requiring novel loss functions or training techniques to successfully improve performance across multiple lp norms. The key to multi-norm robustness is analyzing and mitigating the trade-offs between different perturbation types, and developing strategies that address these trade-offs effectively during the training process.
Logit Pairing Loss#
The concept of a ’logit pairing loss’ in adversarial training aims to improve robustness against multiple lp-norm bounded attacks by mitigating the trade-offs between clean accuracy and robustness against various perturbation types. The core idea revolves around enforcing similarity in the logit distributions of adversarial examples generated under different norms (e.g., l1 and l∞). This approach leverages the observation that simply improving robustness against one norm can detrimentally affect robustness against others. By reducing the discrepancy in logits for correctly classified examples across multiple norms, the model learns to generalize better and achieve improved union accuracy (performance across the union of all considered attacks). The effectiveness hinges on the selection of appropriate norm pairs for pairing, typically focusing on those exhibiting the strongest trade-offs in robustness. The proposed loss function, whether based on KL-divergence or other similarity metrics, directly addresses the distribution shifts induced by adversarial examples, effectively promoting a more balanced and universally robust model. Theoretical analysis could further illuminate the properties of this loss in the context of distribution shifts and its influence on model generalization.
NT-AT GradientProj#
The heading ‘NT-AT GradientProj’ suggests a method combining natural training (NT) and adversarial training (AT) using gradient projection. NT likely refers to training a model on standard, unperturbed data, aiming for high accuracy. AT, conversely, focuses on robustness against adversarial attacks by incorporating perturbed inputs. Gradient projection is a technique to integrate information from both NT and AT. This approach likely aims to leverage the accuracy benefits of NT while maintaining the robustness of AT. The effectiveness would hinge on the ability of gradient projection to carefully select and combine beneficial updates from both training paradigms, achieving a better accuracy-robustness tradeoff than using either method alone. A key challenge would be to avoid negative transfer from one approach interfering with the other; the method’s success relies on a sophisticated balance.
Universal Robustness#
The concept of “Universal Robustness” in the context of this research paper appears to explore the generalization capabilities of a model trained to be robust against multiple adversarial attacks. It suggests that robustness achieved against a diverse set of known adversarial attacks translates to improved performance against unknown or unseen attacks and corruptions. The paper investigates whether models trained with the proposed RAMP framework exhibit this property. This is a crucial aspect because real-world adversarial attacks are rarely limited to a single type or magnitude of perturbation and may involve unforeseen, diverse corruptions. The success of RAMP in achieving superior universal robustness suggests its efficacy in developing more practical and resilient AI systems. The evaluation involving unseen adversaries and natural corruptions provides strong evidence for the effectiveness of the proposed method in enhancing the robustness of deep neural networks against a broader range of threats. Universal robustness is not merely about robustness to known attacks but extends to generalization capability against previously unseen adversaries which is a vital attribute of a truly robust AI model.
RAMP Framework#
The RAMP framework, designed to enhance the adversarial robustness of deep neural networks, tackles the challenge of achieving high union accuracy (robustness across multiple lp norms) while maintaining good clean accuracy. It introduces a novel logit pairing loss to address the trade-offs between robustness against different perturbation types, effectively mitigating the loss of robustness against one norm when enhancing another. The framework also strategically integrates information from natural training into adversarial training via gradient projection. This technique is shown to improve the trade-off between accuracy and adversarial robustness. RAMP can be easily adapted for both fine-tuning and full adversarial training, demonstrating its versatility and effectiveness. Overall, RAMP presents a significant step towards achieving superior universal robustness, generalizing well against both unseen adversaries and natural corruptions.
More visual insights#
More on figures

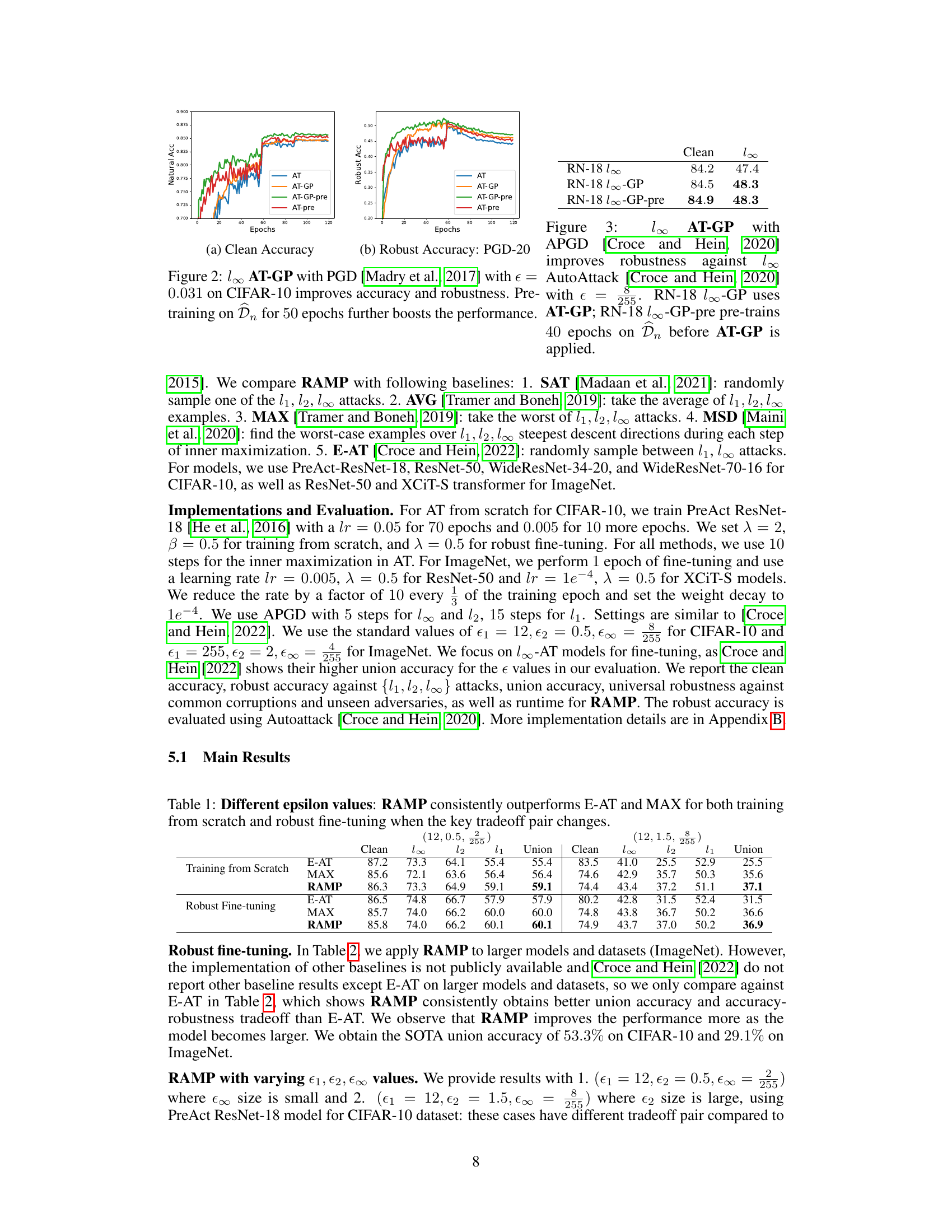
The figure shows two plots: (a) Clean Accuracy and (b) Robust Accuracy (PGD-20). Both plots compare the performance of four different training methods: AT, AT-GP, AT-GP-pre, and AT-pre against the number of epochs. AT-GP represents adversarial training with gradient projection, AT-GP-pre represents pre-training on natural data before adversarial training with gradient projection, and AT-pre represents pre-training on natural data before adversarial training. The plots show that AT-GP and AT-GP-pre achieve higher accuracy and robustness compared to AT and AT-pre, and pre-training further improves the performance.
This figure visualizes the change in l1, l2, and l∞ robustness when fine-tuning a pre-trained l∞-adversarial training (AT) model with l1 examples. It shows that standard fine-tuning and E-AT significantly reduce the l∞ robustness after just one epoch. In contrast, the RAMP framework maintains substantially more l∞ robustness and union robustness (overall robustness against multiple norms). This highlights the effectiveness of RAMP in mitigating the trade-offs between robustness against different perturbation types.
This figure shows the effect of gradient projection (GP) on adversarial training (AT). It compares the performance of standard AT, AT with GP (AT-GP), AT-GP with pre-training (AT-GP-pre), and standard AT with pre-training (AT-pre) on CIFAR-10. The plots display the clean accuracy and robustness against the l∞-norm perturbation using Projected Gradient Descent (PGD). The results demonstrate that incorporating GP improves both clean accuracy and robustness and that pre-training further enhances the performance.

This figure visualizes the changes in robustness against different lp norms (l1, l2, l∞) when fine-tuning a model pre-trained with adversarial training on the l∞ norm. It shows that standard fine-tuning with l1 examples significantly reduces the robustness against the l∞ norm, while the proposed RAMP method better preserves both the l∞ robustness and the overall union robustness (robustness across multiple norms). The histograms illustrate the distribution of accuracy across different perturbation levels after applying each method.
This figure visualizes the changes in l1, l2, and l∞ robustness during the fine-tuning of an l∞-adversarial training model using l1 examples. The results are compared against standard adversarial training and another defense called E-AT. The key observation is that standard fine-tuning causes a substantial drop in l∞ robustness after just one epoch, whereas the proposed RAMP method better maintains both l∞ and overall (union) robustness. This highlights RAMP’s effectiveness in mitigating the trade-off between robustness against different perturbation types.

This figure visualizes the trade-offs among robustness against different perturbation norms (l1, l2, and l∞) during the fine-tuning process. It compares the performance of three methods: standard l1 fine-tuning, E-AT (Extreme Adversarial Training), and RAMP (Robustness Against Multiple Perturbations). The histograms show that while standard l1 fine-tuning and E-AT significantly reduce l∞ robustness after one epoch, RAMP effectively maintains l∞ and union robustness, demonstrating its effectiveness in balancing the trade-offs between clean accuracy and robustness against multiple norms.
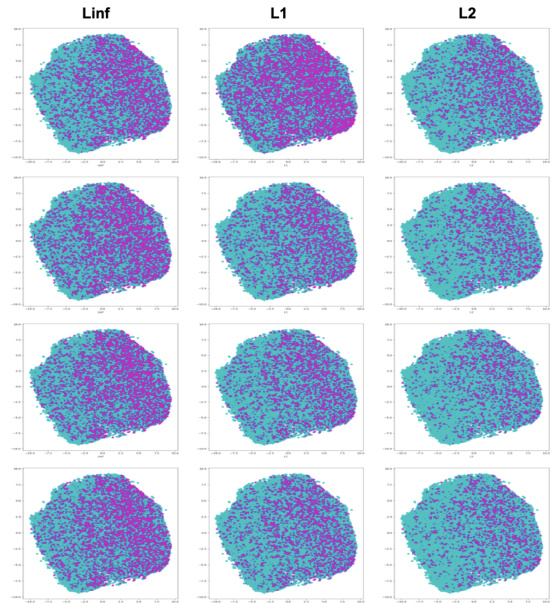
This figure visualizes the changes in l1, l2, and l∞ robustness when fine-tuning a pre-trained l∞-adversarial training (AT) model using l1 examples. It shows a significant drop in l∞ robustness after just one epoch of fine-tuning with standard AT and E-AT methods. In contrast, the RAMP method effectively preserves both l∞ and union robustness, indicating its superior ability to maintain robustness against multiple norms.
More on tables

This table presents the results of robust fine-tuning experiments using various models and datasets (CIFAR-10 and ImageNet). It compares the performance of RAMP against E-AT, highlighting RAMP’s superior union accuracy (robustness against multiple perturbation types) while maintaining good accuracy. The table showcases the clean accuracy, robustness against different perturbation types (l∞, l2, l1), and the union accuracy for each model and method. The asterisk (*) indicates that additional data was used for pre-training in those specific cases. The results clearly demonstrate RAMP’s improvement in robustness against multiple norms.

This table presents the results of adversarial training from random initialization on CIFAR-10 using the PreAct ResNet-18 model. The results are averaged over 5 independent trials. The table compares the performance of RAMP against several baselines (SAT, AVG, MAX, MSD, E-AT) across multiple metrics: clean accuracy, and robustness against l∞, l2, and l1 attacks, and union accuracy (robustness against all three attacks simultaneously). The results show that RAMP achieves the highest union accuracy while maintaining good clean accuracy, demonstrating its ability to mitigate the trade-offs among different attacks and between accuracy and robustness.

This table presents a comparison of different models’ robustness against common image corruptions and unseen adversarial attacks. The ‘Common Corruptions’ column lists various types of image corruptions, with each column showing the accuracy of the model on that specific corruption. The ‘Avg’ column provides the average accuracy across all corruptions. The ‘Union’ column shows the union accuracy across multiple unseen adversarial attacks. The table compares various models, including ℓ1-AT, ℓ2-AT, ℓ∞-AT, Winninghand, E-AT, MAX, and RAMP. Winninghand is included as a state-of-the-art model for handling natural corruptions.

This table shows the results of fine-tuning with RAMP using pre-trained ResNet-18 models with different lp-norms (l∞, l1, l2) on the CIFAR-10 dataset. The table presents the clean accuracy and robust accuracy against different lp attacks (l∞, l1, l2) as well as the union accuracy, which represents the robustness against all three perturbation types simultaneously. The results highlight RAMP’s effectiveness in improving the robustness against multiple perturbations.

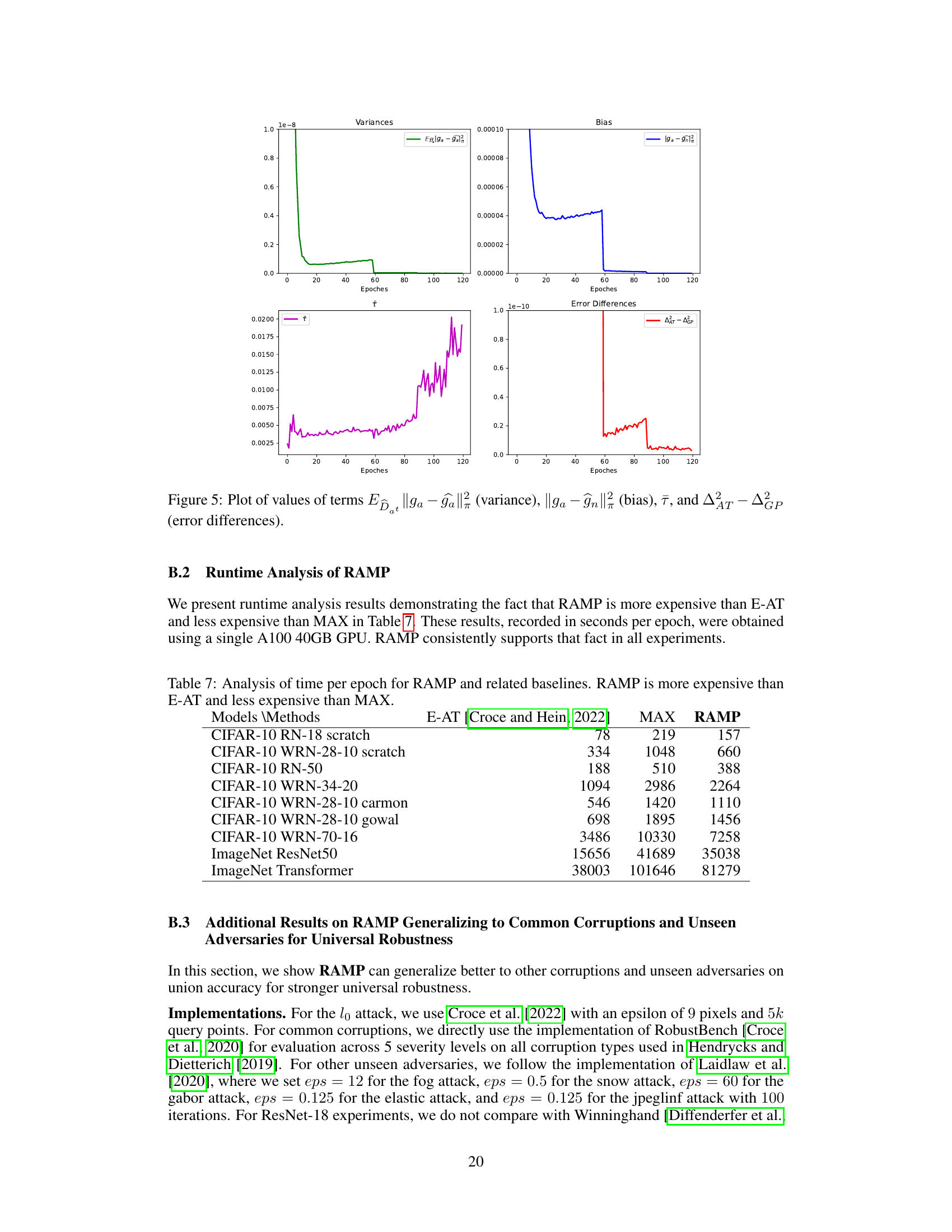
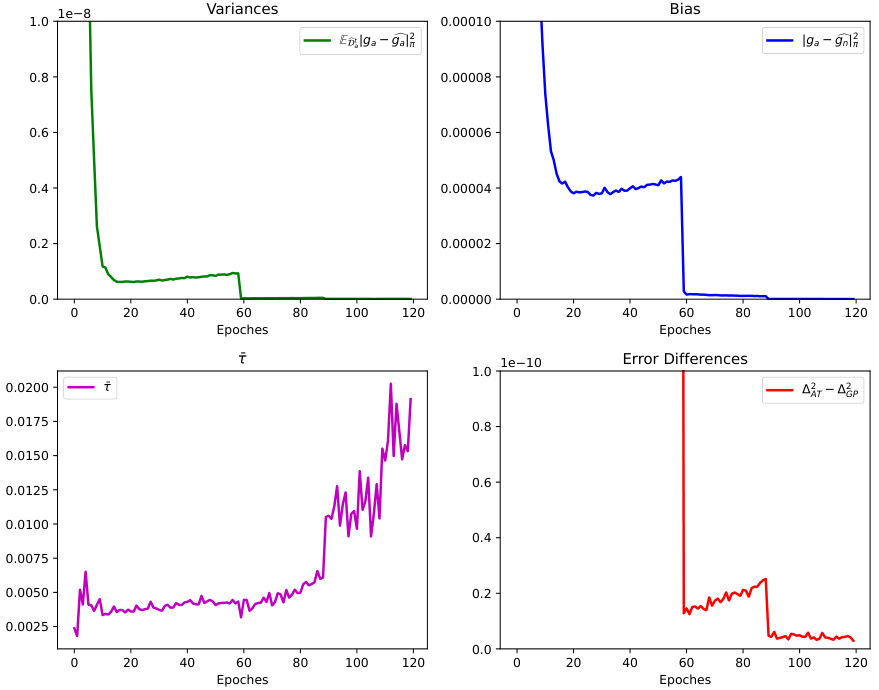
This table presents the estimated values of variance, bias, and the angle between natural and adversarial gradients, along with the calculated difference between the squared errors of adversarial training and gradient projection at various epochs (5, 10, 15, 20, and 60). These values are used to support the theoretical analysis demonstrating the superiority of gradient projection in balancing accuracy and robustness.

This table presents a runtime analysis comparing RAMP against E-AT and MAX. It shows the time (in seconds) taken per epoch for training different models on CIFAR-10 and ImageNet datasets. The results demonstrate that RAMP’s computational cost is higher than E-AT but lower than MAX, offering a balance between efficiency and performance improvements.

This table presents the accuracy of three different models (E-AT, MAX, and RAMP) against common corruptions on the CIFAR-10 dataset using the ResNet-18 architecture. It showcases the models’ robustness to image corruptions.

This table shows the performance of different models (l1-AT, l2-AT, l∞-AT, Winninghand, E-AT, MAX, and RAMP) on CIFAR-10 dataset in terms of their accuracy against common corruptions and unseen adversaries. The common corruptions are evaluated across five severity levels (fog, snow, gabor, elastic, jpeg compression). Unseen adversaries represent different types of attacks not seen during training. The table provides individual accuracies for each corruption type and adversary, the average accuracy across all corruptions/adversaries, and the union accuracy (which represents robustness against the union of all corruptions and adversaries).

This table shows the results of experiments comparing RAMP with E-AT and MAX on CIFAR-10 using different epsilon values for l1, l2, and l∞ attacks. The results demonstrate the consistent superior performance of RAMP across various settings, particularly in achieving higher union accuracy (robustness against multiple perturbation types). The change in the key tradeoff pair (the pair of attacks showing the strongest trade-off) is also highlighted, emphasizing RAMP’s adaptability to different adversarial attack scenarios.

This table presents the results of robust fine-tuning on larger models and datasets, comparing the performance of RAMP against other methods. The models are fine-tuned using additional data for pre-training in some cases. The table evaluates on all CIFAR-10 and ImageNet test points and shows RAMP achieves better union accuracy and accuracy-robustness tradeoff. Results are given for clean accuracy, robustness against l∞, l2, and l1 attacks, and union accuracy.

This table compares the performance of RAMP against E-AT and MAX under different epsilon values for both training from scratch and robust fine-tuning scenarios. It demonstrates RAMP’s superior performance in terms of clean accuracy, l∞, l2, l1 accuracies, and union accuracy across various epsilon configurations.

This table shows the results of experiments conducted using different epsilon values for l1, l2, and l∞ attacks. It compares the performance of RAMP against E-AT and MAX methods for training deep neural networks (DNNs) from scratch and robust fine-tuning. The key tradeoff pair refers to the strongest attack among the three types of attacks (l1, l2, l∞) that have the lowest robustness against other attack types. The table highlights how RAMP consistently outperforms the other two methods across different scenarios.

This table shows the performance comparison of RAMP, E-AT, and MAX under different epsilon values for both training from scratch and robust fine-tuning scenarios. The results demonstrate that RAMP consistently outperforms the other methods in terms of clean accuracy, l∞, l2, l1 accuracy, and especially union accuracy, which is a key metric for multi-perturbation robustness. The table highlights the impact of changing the key trade-off pair (the two attacks with the lowest robustness against each other) on model performance.

This table presents a comparison of the performance of RAMP, E-AT, and MAX under different epsilon values for both training from scratch and robust fine-tuning. It demonstrates that RAMP consistently outperforms the other two methods across various settings, highlighting its effectiveness in enhancing robustness against multiple perturbations.

This table shows the results of the RAMP model compared to E-AT and MAX models for different epsilon values. It demonstrates that RAMP consistently achieves better performance across various metrics, including clean accuracy, robustness against different attacks, and union accuracy, regardless of the specific epsilon values used or whether the model is trained from scratch or fine-tuned.

This table presents the results of experiments comparing the performance of RAMP against E-AT and MAX under different epsilon values for both training from scratch and robust fine-tuning. The key tradeoff pair is identified using a heuristic based on the single-norm robustness of adversarially trained models, where the two models with the lowest robustness against themselves are selected. The results show that RAMP achieves consistently better union accuracy, especially when the key tradeoff pair changes. The table highlights the superior performance of RAMP across various scenarios.

This table shows the results of adversarial training from random initialization on CIFAR-10 using the ResNet-18 model. The table compares the performance of RAMP against several baselines (SAT, AVG, MAX, MSD, E-AT) across multiple metrics including clean accuracy, and robustness against various L-p attacks, culminating in a final union accuracy score. The results highlight that RAMP achieves the best union accuracy with good clean accuracy, indicating its effectiveness in mitigating the trade-offs between accuracy and robustness against multiple perturbations.

This table presents the results of adversarial training from random initialization on CIFAR-10 using the PreAct ResNet-18 model. The table compares the performance of RAMP against several baselines (SAT, AVG, MAX, MSD, E-AT) across five trials. The metrics reported include clean accuracy, robust accuracy against l∞, l2, and l1 attacks, and the union accuracy (a measure of robustness against multiple attack types). RAMP demonstrates superior union robustness with good clean accuracy.

This table compares the performance of RAMP, E-AT, and MAX across different epsilon values for both training from scratch and robust fine-tuning. The results show that RAMP achieves higher clean accuracy, individual robustness against different lp-norms, and overall union accuracy, which demonstrates its effectiveness in boosting robustness across multiple perturbation types.

This table presents a comparison of the performance of RAMP, E-AT, and MAX across different settings of epsilon values for L1, L2, and L∞ attacks. The results are split into two parts, one for models trained from scratch and another for models that underwent robust fine-tuning. The key takeaway is that RAMP consistently shows better performance across all scenarios and demonstrates its superiority in handling multiple perturbation types.

This table shows the results of robust fine-tuning experiments using the RAMP framework with three different logit pairing loss functions: KL divergence, Mean Squared Error (MSE), and Cosine Similarity. The results are compared in terms of clean accuracy and robustness against three different adversarial attack types (l∞, l2, l1), along with overall union accuracy. This helps to analyze the effect of different logit pairing strategies on the model’s performance.

This table compares the performance of different methods on the WideResNet-28-10 model trained from random initialization on the CIFAR-10 dataset. The methods compared include E-AT with and without the trades loss, and RAMP with and without the trades loss. The table shows the clean accuracy, accuracy against individual attacks ($l_\infty$, $l_2$, $l_1$), and union accuracy. The results demonstrate that RAMP, particularly with the trades loss, achieves superior union accuracy compared to E-AT.

This table presents the results of adversarial training from random initialization on CIFAR-10 using the PreAct ResNet-18 model. It compares the performance of RAMP against several baselines (SAT, AVG, MAX, MSD, E-AT) across five trials, evaluating clean accuracy, robustness against l∞, l2, and l1 attacks, and union accuracy (robustness against all three attack types simultaneously). The results show that RAMP achieves the best union robustness and good clean accuracy, indicating its ability to mitigate the tradeoffs among perturbations and robustness/accuracy in this scenario.

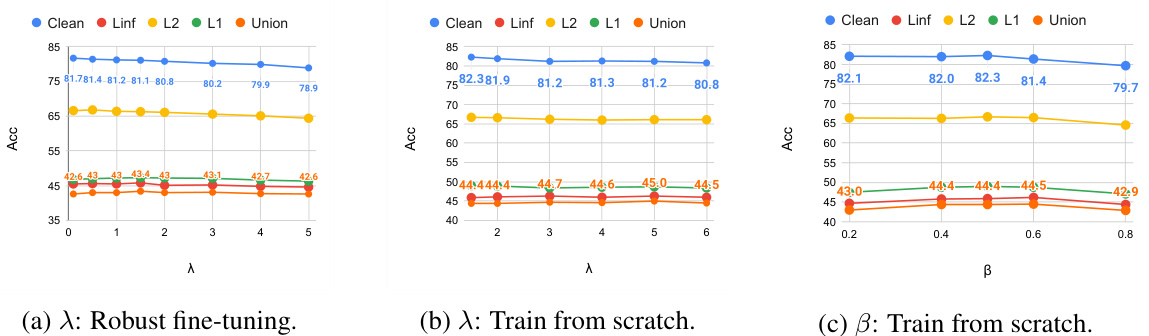
This table shows the results of robust fine-tuning experiments using PreAct ResNet-18 model on CIFAR-10 dataset with varying numbers of epochs (5, 7, 10, and 15). The table compares the performance of RAMP against E-AT (Extreme Adversarial Training) in terms of clean accuracy and union accuracy. Union accuracy is a measure of robustness across multiple adversarial attacks (l1, l2, and l∞). The results demonstrate that RAMP consistently achieves higher union accuracy than E-AT, with the improvement becoming more pronounced as the number of epochs increases.
Full paper#