↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning models struggle with out-of-distribution (OOD) generalization, where the training and testing data come from different distributions. Existing approaches often rely on measuring distances between distributions, which may not effectively capture complex distribution shifts. This paper proposes a novel approach to tackling the problem by representing OOD generalization as learning under data transformations. The core issue is to understand how the shifts of distribution can affect learning, and if we can learn predictors that are invariant to these shifts.
The paper introduces a theoretical framework where training and testing distributions are related through a set of transformations, which can be either known or unknown. The authors propose learning rules that aim to minimize the worst-case error across all possible transformations. These rules are supported by theoretical guarantees on sample complexity in terms of the VC dimension of predictors and transformations. Furthermore, the paper addresses the scenario where the transformation class is unknown, proposing algorithmic reductions to ERM that solve the problem using only an ERM oracle. The proposed algorithms offer a game-theoretic interpretation, where the learner seeks predictors that minimize losses, while an adversary selects transformations that maximize losses. The results provide insights into the sample complexity of transformation-invariant learning and highlight the importance of considering both predictors and transformations when designing robust learning algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on robust machine learning and domain adaptation. It offers a novel theoretical framework for understanding and addressing out-of-distribution generalization, providing new learning rules and algorithmic reductions with associated guarantees. The work opens exciting avenues for future research, including exploring the interplay of predictors and transformations in a game-theoretic setting, designing novel learning algorithms leveraging only ERM oracles, and extending the framework to handle more complex and realistic scenarios.
Visual Insights#
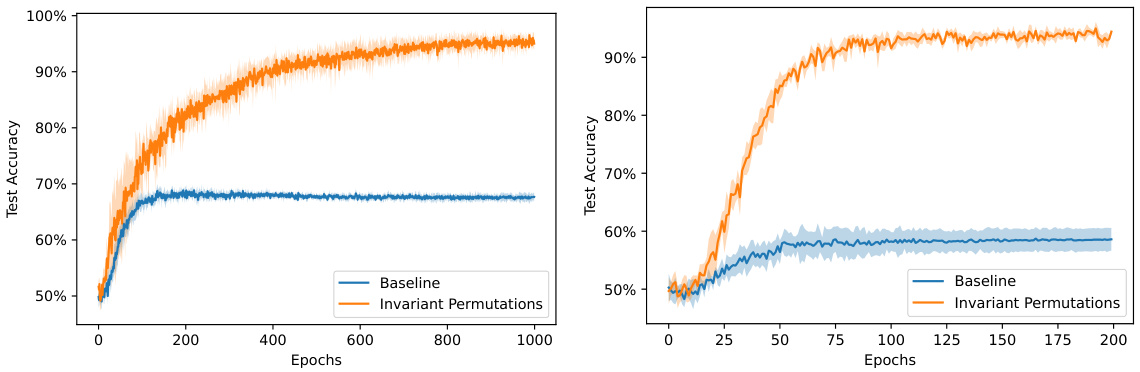
This figure shows the results of two experiments on learning Boolean functions using two different training algorithms. The left plot shows the results for learning the full parity function (f₁) with 18 dimensions, using a training set of 7000 samples and a test set of 1000 samples. Transformations were randomly sampled from the set of all possible permutations (T₁). The right plot shows results for learning a majority-of-subparities function (f₂) with 21 dimensions, using a training set of 5000 samples and a test set of 1000 samples. Transformations were sampled from the set of permutations that leave f₂ invariant (T₂). Both plots compare a baseline algorithm (standard mini-batch SGD) against an algorithm that incorporates data augmentation using the selected transformations.
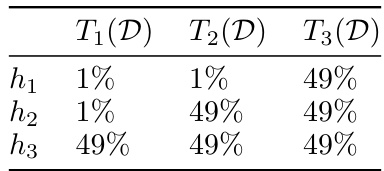
This table shows the error rates of three different predictors (h1, h2, h3) on three different transformed distributions (T1(D), T2(D), T3(D)). The error rates represent the percentage of misclassifications for each predictor on each distribution. This example illustrates a scenario where minimizing the worst-case error (Objective 1) might not be the optimal strategy, as it could lead to choosing a predictor with high error across all transformations. In contrast, another predictor might perform very well on most transformations.
Full paper#



















