TL;DR#
Training large-scale deep learning models often relies on distributed learning methods like asynchronous SGD (ASGD). However, effectively incorporating momentum, a technique known to improve convergence, into ASGD has proven difficult; naive implementations often hinder convergence. This has motivated research into sophisticated momentum techniques for ASGD, but these often lack theoretical justification or practical effectiveness.
This paper introduces Ordered Momentum (OrMo), a new method that successfully integrates momentum into ASGD. OrMo achieves this by organizing gradients based on their iteration order. The key contribution is the theoretical proof of OrMo’s convergence for non-convex problems, which holds even with delay-adaptive learning rates, a significant advancement over existing ASGD approaches that often depend on the maximum delay. Furthermore, the paper presents empirical evidence demonstrating OrMo’s superior convergence performance compared to standard ASGD and other momentum-enhanced ASGD methods.
Key Takeaways#
Why does it matter?#
This paper is important because it proposes a novel method, Ordered Momentum (OrMo), that significantly improves the convergence performance of asynchronous SGD (ASGD), a widely used distributed learning method. OrMo addresses the long-standing challenge of efficiently incorporating momentum into ASGD without hindering convergence, providing both theoretical guarantees and empirical validation. This offers a significant advancement in the field of distributed optimization, which is crucial for training large-scale deep learning models.
Visual Insights#

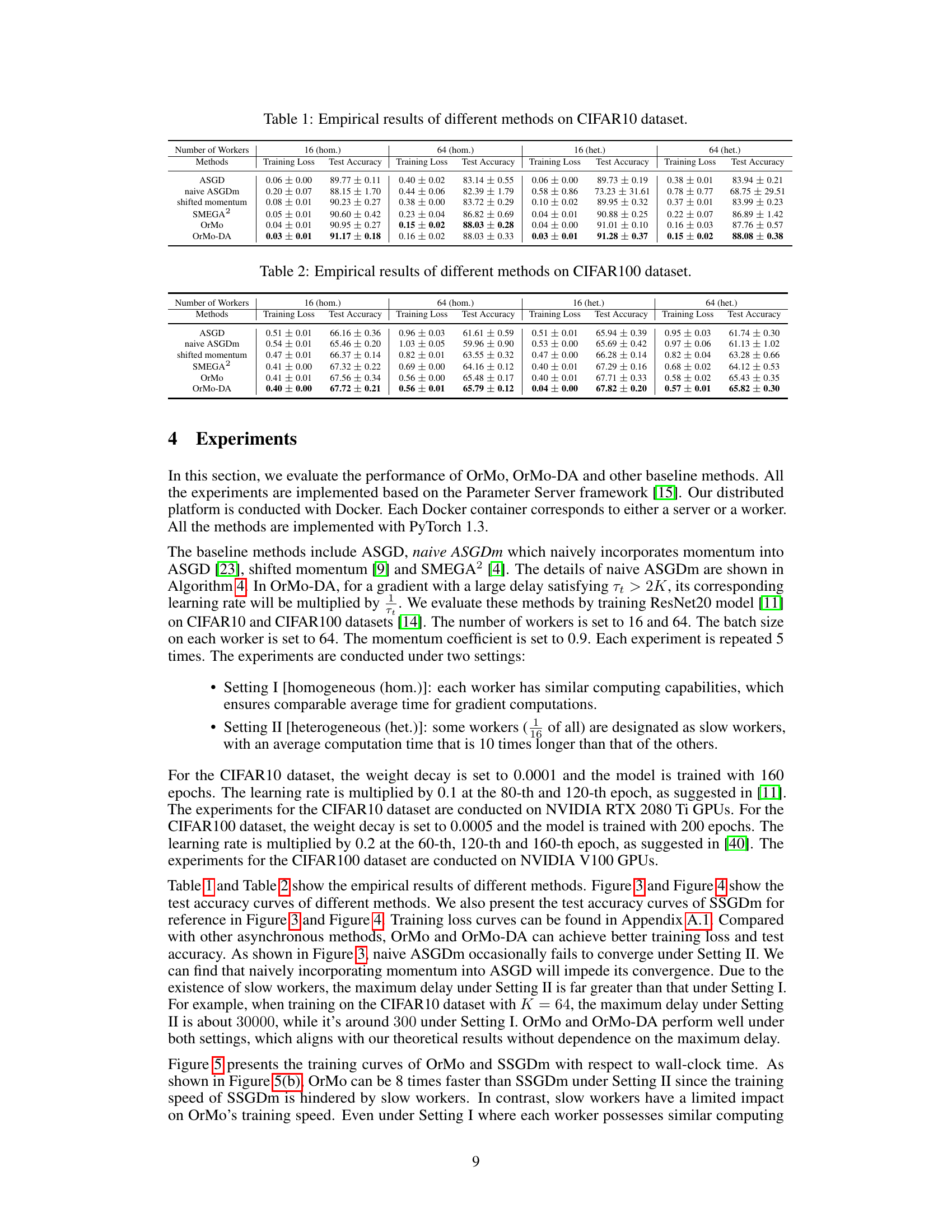
🔼 This figure illustrates the momentum term (u10) calculation in the Synchronous SGD with momentum (SSGDm) algorithm when there are 4 workers (K=4). Each colored block represents a scaled gradient (ηg) from a worker. Blue blocks represent gradients that have already arrived at the server, while red blocks represent gradients that haven’t yet arrived. The equation shows how the momentum is a weighted sum of these gradients, with weights determined by the momentum coefficient (β) and the order of arrival. The order is crucial because SSGDm uses a synchronous scheduler, meaning all gradients from a given iteration must arrive before the model is updated. Gradients from earlier iterations are weighted less (higher power of β).
read the caption
Figure 1: An example of the momentum term u10 in SSGDm when K = 4. The gradients shown in red indicate those having not arrived at the server. In this case, u10 = β² × (ng⁰ + ng⁰ + ng⁰ + ng⁰) + β¹ × (ng₁ + ng₁ + ng₁ + ng₁) + β⁰ × (ng₄ + ng₄).

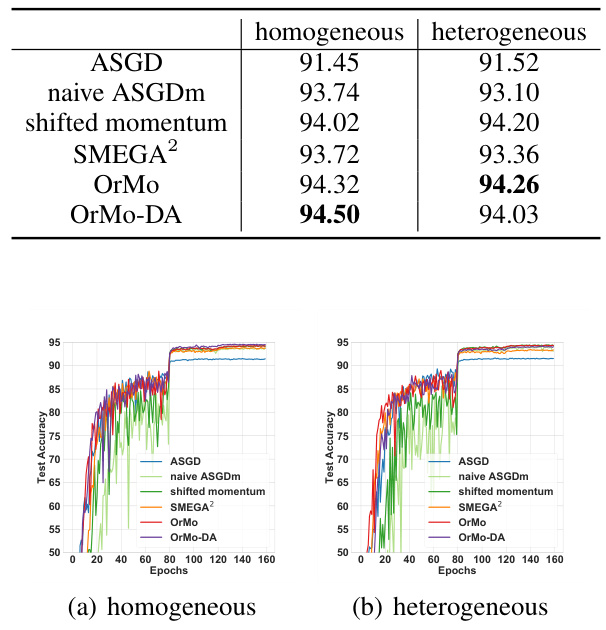
🔼 The table presents the empirical results of various asynchronous SGD methods on the CIFAR10 dataset. It compares the training loss and test accuracy of ASGD, naive ASGDm, shifted momentum, SMEGA2, OrMo, and OrMo-DA under different settings (homogeneous and heterogeneous worker configurations with 16 and 64 workers). The results highlight the performance of the proposed OrMo and OrMo-DA methods.
read the caption
Table 1: Empirical results of different methods on CIFAR10 dataset.
In-depth insights#
Async SGD Momentum#
Asynchronous Stochastic Gradient Descent (Async SGD) is a widely used method for training large-scale machine learning models in a distributed setting. However, incorporating momentum, a technique that accelerates convergence and improves generalization, into Async SGD is challenging because of the asynchronous updates from multiple worker nodes. Naive approaches often hinder convergence or even lead to divergence. The core issue lies in the inconsistent order of gradient updates arriving at the central parameter server. This necessitates innovative approaches to maintain the beneficial properties of momentum in an asynchronous environment. Effective strategies focus on carefully managing and ordering the incoming gradient updates to preserve the integrity and effectiveness of the momentum term. This often involves techniques to either explicitly schedule or implicitly weigh the gradients based on their staleness or iteration index. Theoretical analyses of these approaches are crucial for proving convergence guarantees, especially in non-convex settings, which often require more sophisticated analyses than their synchronous counterparts. Establishing convergence requires accounting for the inherent delays and staleness of asynchronous updates. Experimental results demonstrate whether these sophisticated approaches improve both convergence rates and generalization performance compared to Async SGD without momentum or naive momentum implementations. Ultimately, research in Async SGD momentum seeks to reconcile the speed and scalability benefits of asynchronous updates with the convergence-boosting capabilities of momentum.
Ordered Momentum#
The concept of “Ordered Momentum” presents a novel approach to asynchronous stochastic gradient descent (ASGD) optimization. Traditional momentum methods struggle in asynchronous settings due to the unpredictable arrival order of gradients. Ordered Momentum addresses this by organizing gradients based on their iteration indices before incorporating them into the momentum update. This systematic approach ensures that gradients are processed in a chronological manner, mimicking the behavior of synchronous momentum while leveraging the efficiency of asynchronous updates. The theoretical analysis demonstrates the convergence of Ordered Momentum under specific conditions, offering a more stable and efficient optimization strategy for large-scale deep learning models. A key advantage is its independence from maximum delay, unlike many existing ASGD with momentum methods, allowing it to achieve better convergence performance in heterogeneous environments. This methodology enhances the effectiveness of momentum in asynchronous settings, especially crucial for scenarios with varying worker compute capabilities.
Convergence Analysis#
A rigorous convergence analysis is crucial for validating the effectiveness and reliability of any optimization algorithm. In the context of asynchronous stochastic gradient descent (ASGD), convergence analysis becomes particularly challenging due to the inherent complexities introduced by the asynchronous updates. This analysis would typically involve demonstrating that the algorithm’s iterates converge to a stationary point of the objective function under specific conditions and assumptions. Key aspects to explore would be the impact of delays in gradient updates and the choice of learning rates (constant vs. delay-adaptive) on the convergence behavior. A theoretical analysis should formally establish convergence rates, ideally providing bounds on the convergence speed, and ideally showing how these rates depend on various parameters, such as the number of workers, the maximum delay, and the learning rate. A well-structured analysis would likely involve using mathematical tools from optimization theory and probability to address the stochastic nature of ASGD updates. The assumptions made (e.g., about the smoothness and boundedness of the objective function and the stochastic gradients) should be clearly stated and justified. Finally, the analysis should carefully consider the implications of the asynchronous updates and how they influence the overall convergence properties. The comparison of theoretical results with empirical findings is also essential to validate the accuracy and provide a comprehensive understanding of the algorithm’s behavior in practice.
Empirical Results#
An Empirical Results section in a research paper should present a detailed and insightful analysis of experimental findings. It should clearly state the methodologies used, including datasets, model architectures, and evaluation metrics. Quantitative results should be presented clearly, often using tables and figures, showing key performance indicators and comparison with relevant baselines. Statistical significance should be addressed to provide confidence in the findings. The discussion should not simply state numbers but should analyze trends, highlight unexpected results, and explore potential reasons for observed patterns. Error bars or confidence intervals are essential to convey uncertainty and reproducibility. A strong section would also relate the empirical findings to the theoretical contributions, showing a cohesive narrative between theory and practice. For example, the experimental results could demonstrate the efficacy of a novel algorithm compared to existing ones in different settings, or they could showcase how algorithm parameters affect performance, validating or challenging theoretical claims. A thoughtful discussion, connecting experimental findings to existing knowledge, and pointing out limitations is critical to enhance the value and impact of the research.
Future Work#
The ‘Future Work’ section of this research paper would ideally explore several avenues. Extending the theoretical analysis to cover more general settings, such as non-convex problems with more complex structures or non-i.i.d. data distributions, would significantly strengthen the paper’s contributions. Investigating the impact of different communication schedulers beyond the parameter server model, such as decentralized approaches, would provide valuable insights into OrMo’s adaptability and robustness. Furthermore, a comprehensive empirical evaluation should be conducted. This should encompass a broader range of datasets and network architectures, thereby demonstrating its generalizability and practical applicability. Finally, exploring the integration of OrMo with other advanced optimization techniques, such as variance reduction or adaptive learning rate methods, could result in further performance improvements. Analyzing OrMo’s performance under various levels of network heterogeneity and delays would also enhance our understanding of its capabilities in real-world distributed environments.
More visual insights#
More on figures

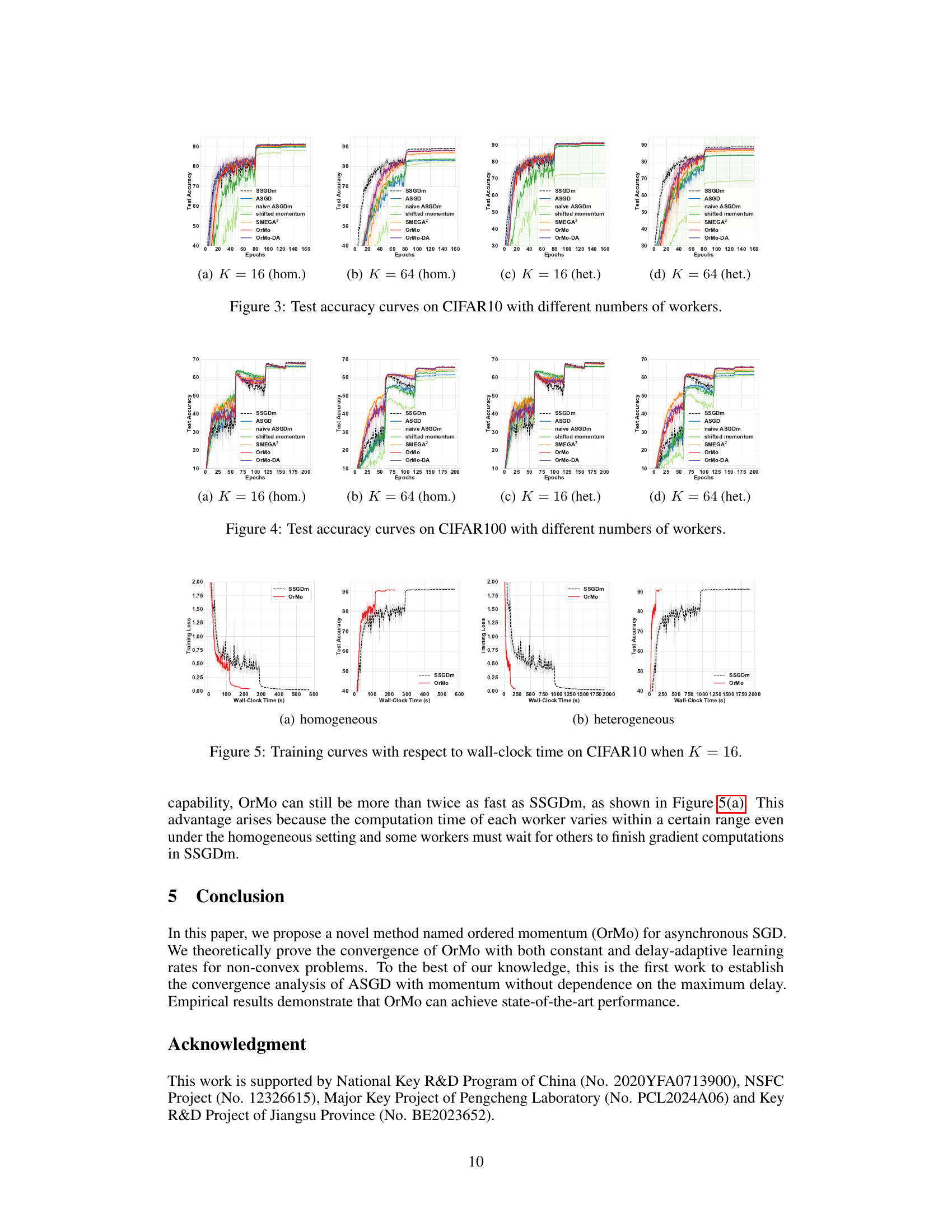
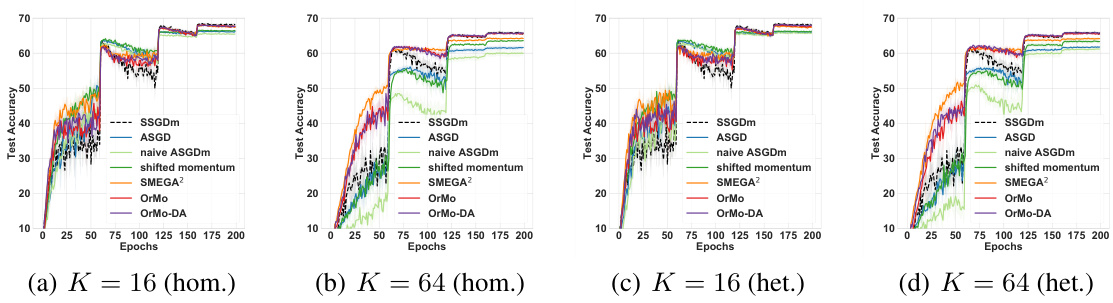
🔼 This figure displays test accuracy curves for various asynchronous SGD methods (ASGD, naive ASGDm, shifted momentum, SMEGA2, OrMo, OrMo-DA) and synchronous SGD with momentum (SSGDm) on the CIFAR10 dataset. The experiments were conducted with different numbers of workers (16 homogeneous, 64 homogeneous, 16 heterogeneous, 64 heterogeneous), illustrating the performance of each method under varying degrees of worker heterogeneity and concurrency. The x-axis represents the number of training epochs, and the y-axis represents the test accuracy. The figure shows the impact of different momentum strategies and worker configurations on the convergence and generalization performance of the different methods.
read the caption
Figure 3: Test accuracy curves on CIFAR10 with different numbers of workers.
🔼 This figure compares the test accuracy of various asynchronous SGD methods (ASGD, naive ASGDm, shifted momentum, SMEGA2, OrMo, OrMo-DA) against synchronous SGD with momentum (SSGDm) across different numbers of workers (16 and 64) and worker heterogeneity (homogeneous and heterogeneous settings). Each subfigure shows the accuracy over epochs for one specific setting of the experiment. The results show the impact of worker configuration on the performance of the algorithms, with OrMo and OrMo-DA generally performing better.
read the caption
Figure 3: Test accuracy curves on CIFAR10 with different numbers of workers.

🔼 This figure compares the training curves of OrMo and SSGDm with respect to wall-clock time on CIFAR10 when the number of workers K is set to 16. The left side shows the results for a homogeneous setting where all workers have similar computing capabilities, while the right side shows the results for a heterogeneous setting where some workers are significantly slower than others. The plots show both training loss and test accuracy over time. The figure highlights OrMo’s superior training speed, especially in heterogeneous settings where slow workers significantly impact SSGDm’s performance.
read the caption
Figure 5: Training curves with respect to wall-clock time on CIFAR10 when K = 16.

🔼 This figure presents the training loss curves for various asynchronous SGD methods and synchronous SGD with momentum (SSGDm) on the CIFAR10 dataset. It shows the training loss over epochs for four different scenarios: 16 homogeneous workers, 64 homogeneous workers, 16 heterogeneous workers, and 64 heterogeneous workers. The purpose is to compare the convergence behavior of different momentum methods (naive ASGDm, shifted momentum, SMEGA2, OrMo, and OrMo-DA) against standard ASGD and SSGDm under various workload conditions.
read the caption
Figure 6: Training loss curves of different methods on CIFAR10 dataset with different numbers of workers.

🔼 This figure compares the training loss curves of various asynchronous SGD methods, including ASGD, naive ASGDm, shifted momentum, SMEGA2, OrMo, and OrMo-DA, across different numbers of workers (16 homogeneous, 64 homogeneous, 16 heterogeneous, and 64 heterogeneous). The curves illustrate the convergence speed and stability of each method under homogeneous and heterogeneous worker setups, highlighting the performance of OrMo and OrMo-DA in handling asynchronous updates and potential delays.
read the caption
Figure 6: Training loss curves of different methods on CIFAR10 dataset with different numbers of workers.
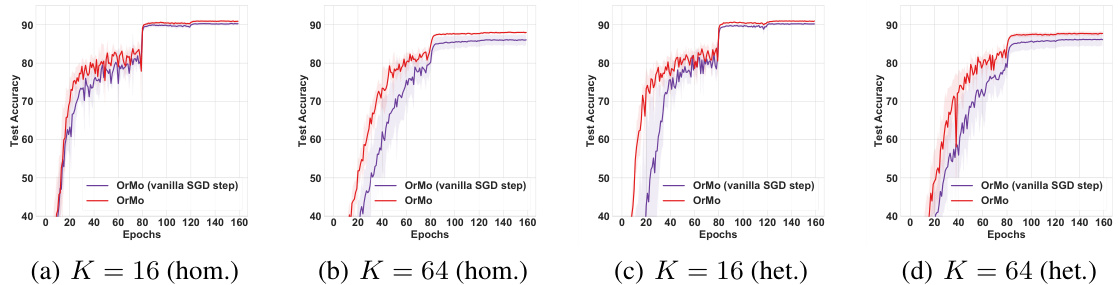
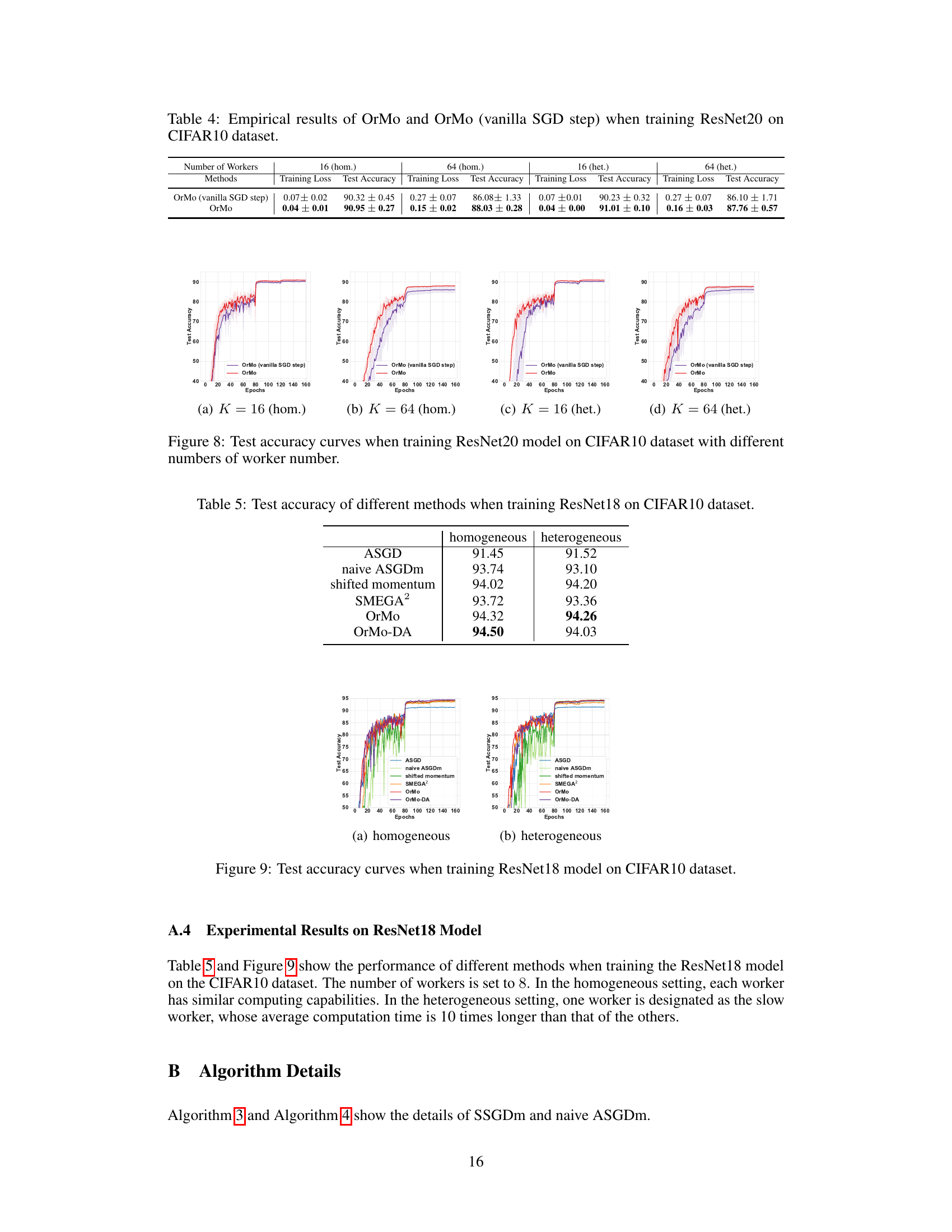
🔼 This figure compares the test accuracy of OrMo and OrMo (vanilla SGD step) across different settings. The four subfigures (a-d) show results for different numbers of workers (K) and worker heterogeneity (homogeneous vs. heterogeneous). OrMo consistently demonstrates superior test accuracy in all cases.
read the caption
Figure 8: Test accuracy curves when training ResNet20 model on CIFAR10 dataset with different numbers of worker number.
🔼 This figure contains four sub-figures showing the test accuracy curves of different methods on the CIFAR10 dataset. Each sub-figure corresponds to a different number of workers: 16 (homogeneous), 64 (homogeneous), 16 (heterogeneous), and 64 (heterogeneous). The methods compared include ASGD, naive ASGDm, shifted momentum, SMEGA2, OrMo, and OrMo-DA. The x-axis represents the number of epochs, and the y-axis represents the test accuracy. The curves show how the test accuracy changes over the training epochs for each method and worker configuration, highlighting the relative performance of each method in different settings (homogeneous vs. heterogeneous worker setups).
read the caption
Figure 3: Test accuracy curves on CIFAR10 with different numbers of workers.
More on tables

🔼 This table presents the training loss and test accuracy achieved by various asynchronous stochastic gradient descent (ASGD) methods on the CIFAR-10 dataset. The methods compared include ASGD, naive ASGDm (naively incorporating momentum), shifted momentum, SMEGA2, OrMo (ordered momentum), and OrMo-DA (OrMo with delay-adaptive learning rate). Results are shown for both homogeneous (similar worker capabilities) and heterogeneous (heterogeneous worker capabilities) worker settings, with 16 and 64 workers in each setting.
read the caption
Table 1: Empirical results of different methods on CIFAR10 dataset.

🔼 This table presents a comparison of the performance of various asynchronous stochastic gradient descent (ASGD) methods on the CIFAR-10 dataset. The methods compared include ASGD, naive ASGDm (naively incorporating momentum into ASGD), shifted momentum, SMEGA2, OrMo (ordered momentum), and OrMo-DA (OrMo with delay-adaptive learning rates). The results are shown for different numbers of workers (16 and 64) under both homogeneous (hom.) and heterogeneous (het.) settings. For each setting and number of workers, the table displays the training loss and test accuracy achieved by each method.
read the caption
Table 1: Empirical results of different methods on CIFAR10 dataset.

🔼 This table presents the empirical results of two different methods, OrMo and OrMo (vanilla SGD step), when training a ResNet20 model on the CIFAR10 dataset. It shows the training loss and test accuracy for both methods under four different scenarios: 16 workers with homogeneous computing capabilities, 64 workers with homogeneous capabilities, 16 workers with heterogeneous capabilities, and 64 workers with heterogeneous capabilities. The results demonstrate the impact of the parameter update rule in OrMo on the model’s performance.
read the caption
Table 4: Empirical results of OrMo and OrMo (vanilla SGD step) when training ResNet20 on CIFAR10 dataset.
Full paper#