TL;DR#
Graph Transformers, while powerful, struggle with capturing long-range dependencies and hierarchical structures present in many real-world graphs, hindering their performance. Existing methods often fall short in addressing these limitations. This research introduces a novel Hierarchical Distance Structural Encoding (HDSE) method to overcome this challenge.
HDSE leverages graph hierarchy distances to effectively encode multi-level hierarchical structures within graphs. The method is seamlessly integrated into the attention mechanism of existing graph transformers, allowing for simultaneous use with other positional encodings. Extensive experiments demonstrate HDSE’s superiority across multiple graph-level datasets, significantly improving performance compared to state-of-the-art models. Furthermore, a high-level HDSE adaptation effectively addresses scalability issues for large graphs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with graph neural networks and transformers. It directly addresses limitations of existing methods by introducing a novel encoding scheme that significantly boosts performance on various graph-level tasks. The theoretical analysis and empirical results provide strong evidence for the effectiveness of HDSE, offering a valuable tool and direction for future research in graph representation learning. The scalability aspects are particularly important for handling real-world large-scale graphs, opening up new avenues for applications in various domains.
Visual Insights#

🔼 This figure illustrates the HDSE method and its integration into graph transformers. HDSE leverages graph hierarchy distances (GHD) to encode node distances at multiple levels of a graph’s hierarchy. The figure depicts the calculation of GHD at different levels (GHD⁰, GHD¹, GHD²) and how these distances are incorporated into the attention mechanism of the transformer using a novel framework. The color intensity of the GHD matrix represents the distance between nodes – darker colors indicate longer distances. The integration allows for the simultaneous use of HDSE with other positional encodings.
read the caption
Figure 1: Overview of our proposed hierarchical distance structural encoding (HDSE) and its integration with graph transformers. HDSE uses the graph hierarchy distance (GHD, refer to Definition 1) that can capture interpretable patterns in graph-structured data by using diverse graph coarsening algorithms. Darker colors indicate longer distances.
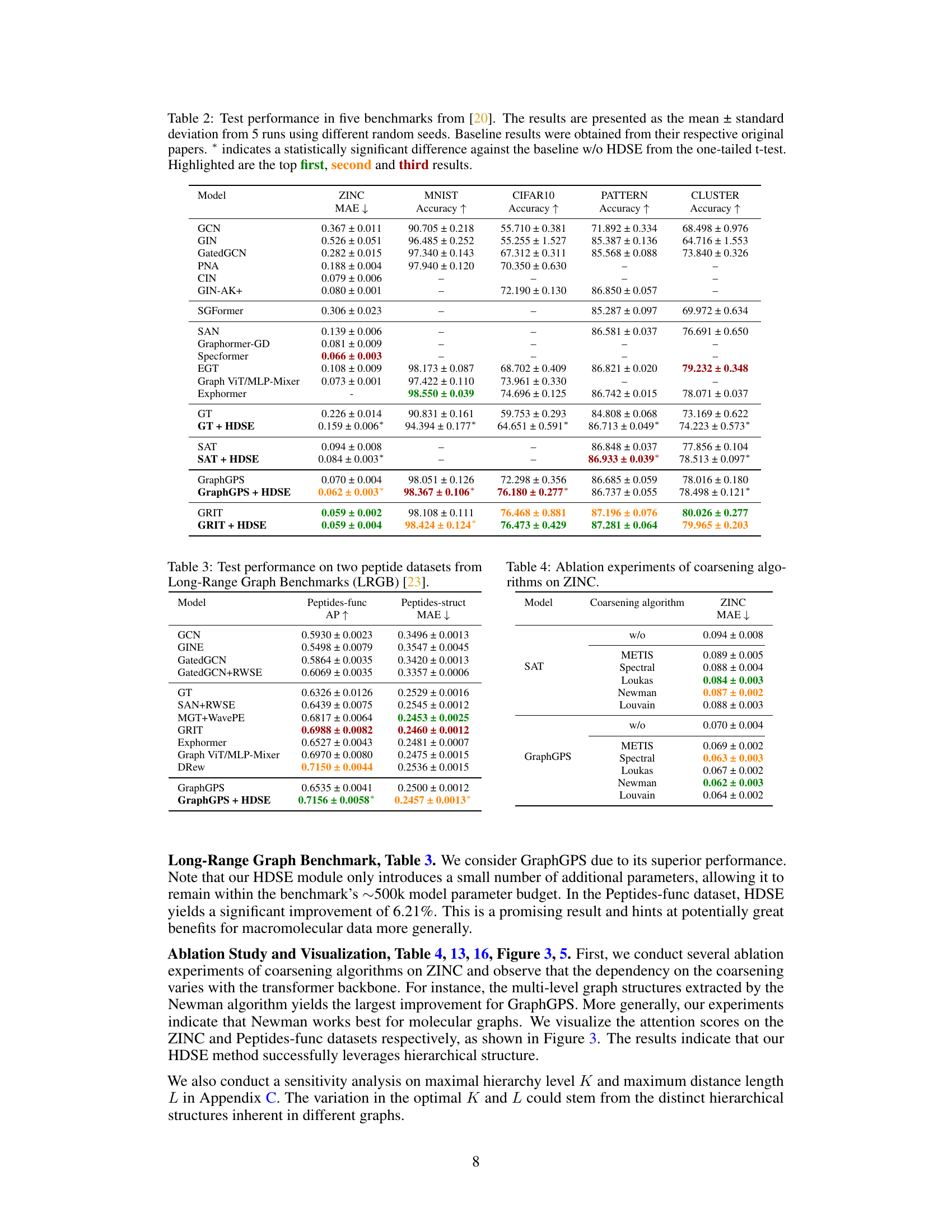
🔼 This table presents the results of graph classification and regression experiments on five benchmark datasets from the Benchmarking GNNs paper [20]. The table compares the performance of several graph transformer models, both with and without the proposed HDSE method. The results are reported as the mean and standard deviation across five runs with different random seeds. Statistically significant improvements achieved by using HDSE are marked with an asterisk.
read the caption
Table 2: Test performance in five benchmarks from [20]. The results are presented as the mean ± standard deviation from 5 runs using different random seeds. Baseline results were obtained from their respective original papers. * indicates a statistically significant difference against the baseline w/o HDSE from the one-tailed t-test. Highlighted are the top first, second and third results.
In-depth insights#
HDSE: Core Concept#
The core concept of Hierarchical Distance Structural Encoding (HDSE) revolves around leveraging the hierarchical nature of graph structures for enhanced graph representation learning. HDSE introduces a novel encoding scheme that captures multi-level distances between nodes, moving beyond simple shortest path distances. By integrating graph coarsening techniques, HDSE effectively models node relationships across various hierarchical levels, capturing both local and global structural patterns. This multi-level encoding is seamlessly integrated into existing graph transformer architectures, enhancing the attention mechanism to weigh node interactions based on their hierarchical distance. This enhances the model’s ability to discern complex, long-range relationships and hierarchical structures often present in real-world graphs, such as molecules and social networks. The theoretical analysis demonstrates HDSE’s superiority in terms of expressiveness and generalization over traditional methods. Finally, a high-level HDSE variant addresses the scalability challenges of graph transformers on massive graphs, effectively biasing the attention mechanism towards hierarchical structures while maintaining computational efficiency.
Transformer Integration#
Integrating transformers into existing graph neural network (GNN) architectures presents a unique set of challenges and opportunities. A naive approach of simply replacing the message-passing layers with transformer blocks often fails to capture the crucial structural information inherent in graph data. Effective integration requires careful consideration of how to encode the graph’s topology and node relationships in a way that is compatible with the transformer’s attention mechanism. This might involve using novel positional encodings specifically designed for graphs, or developing methods to incorporate adjacency matrices directly into the attention calculation. Another key aspect is scalability, as the computational complexity of transformers can be prohibitive for large graphs. Strategies for addressing this limitation include sparse attention mechanisms, hierarchical graph representations, or techniques to reduce the effective input size. Successful integration could lead to GNNs that are more expressive, capable of capturing long-range dependencies, and more robust to over-smoothing issues often encountered in traditional GNNs. The key is to find the optimal balance between leveraging the strengths of both architectures without sacrificing the benefits of either.
Large Graph Scaling#
Scaling graph neural networks (GNNs) to massive graphs presents significant challenges due to the quadratic complexity of self-attention mechanisms. Existing approaches often rely on sampling techniques, which compromise the expressiveness of the model. This paper introduces a novel approach that addresses this issue by incorporating hierarchical distance structural encoding (HDSE) and effectively biases the linear transformers towards graph hierarchies. High-level HDSE is particularly important, as it leverages graph coarsening to efficiently reduce the number of nodes. This allows for meaningful distance calculations across multiple levels of the hierarchy. The method significantly reduces the computational burden while maintaining high efficiency. Theoretical analysis demonstrates the superiority of HDSE in terms of expressiveness and generalization. Empirical results on large-scale node classification datasets confirm that the HDSE approach provides excellent scalability and accuracy while preserving efficiency. The method significantly outperforms state-of-the-art models in terms of both accuracy and efficiency on multiple large graphs.
Expressiveness/Generalization#
The expressiveness and generalization capabilities of a model are critical aspects of its performance, especially when dealing with complex data like graphs. Expressiveness refers to a model’s ability to represent the underlying data distribution, capturing nuanced relationships and avoiding oversimplification. Generalization, on the other hand, is the model’s capacity to perform well on unseen data after training, indicating its robustness beyond the training set. In graph-related machine learning, a model’s ability to capture hierarchical and long-range dependencies significantly impacts expressiveness, as does the model’s capacity to integrate multiple structural features. Methods that improve expressiveness often do so at the cost of increased computational resources, and thus optimization techniques for balancing expressiveness with efficiency are crucial. Furthermore, theoretical analysis and empirical validation are both essential to support claims on expressiveness and generalization, establishing a rigorous foundation for trustworthy results.
Future Work#
Future research directions stemming from this hierarchical distance structural encoding (HDSE) method could explore several promising avenues. Extending HDSE to other graph neural network architectures beyond transformers would broaden its applicability and impact. Investigating the impact of different graph coarsening algorithms on HDSE’s performance, potentially developing adaptive or hybrid approaches, is crucial. A deep dive into the theoretical understanding of HDSE’s expressiveness and generalisation capabilities, possibly through connections to existing graph isomorphism tests, would strengthen the foundation. Addressing the scalability challenges for extremely large graphs, such as optimizing memory usage and computation time, is a practical priority. Finally, empirical evaluations on a wider range of graph datasets, particularly those with complex heterogeneous relationships and varying levels of noise, are needed to fully assess the robustness and effectiveness of the HDSE method.
More visual insights#
More on figures

🔼 This figure shows examples of graph coarsening results and the resulting hierarchy distances calculated using HDSE. The left side demonstrates HDSE’s ability to identify chemical substructures (motifs) in molecule graphs, highlighting the interpretability of HDSE. The right side shows how HDSE successfully distinguishes between two graphs (Dodecahedron and Desargues) that are indistinguishable using only shortest path distance (SPD), showcasing the superior expressiveness of HDSE.
read the caption
Figure 2: Examples of graph coarsening results and hierarchy distances. Left: HDSE can capture chemical motifs such as CF3 and aromatic rings on molecule graphs. Right: HDSE can distinguish the Dodecahedron and Desargues graphs. The Dodecahedral graph has 1-level hierarchy distances of length 2 (indicated by the dark color), while the Desargues graph doesn't. In contrast, the GD-WL test with SPD cannot distinguish these graphs [89].
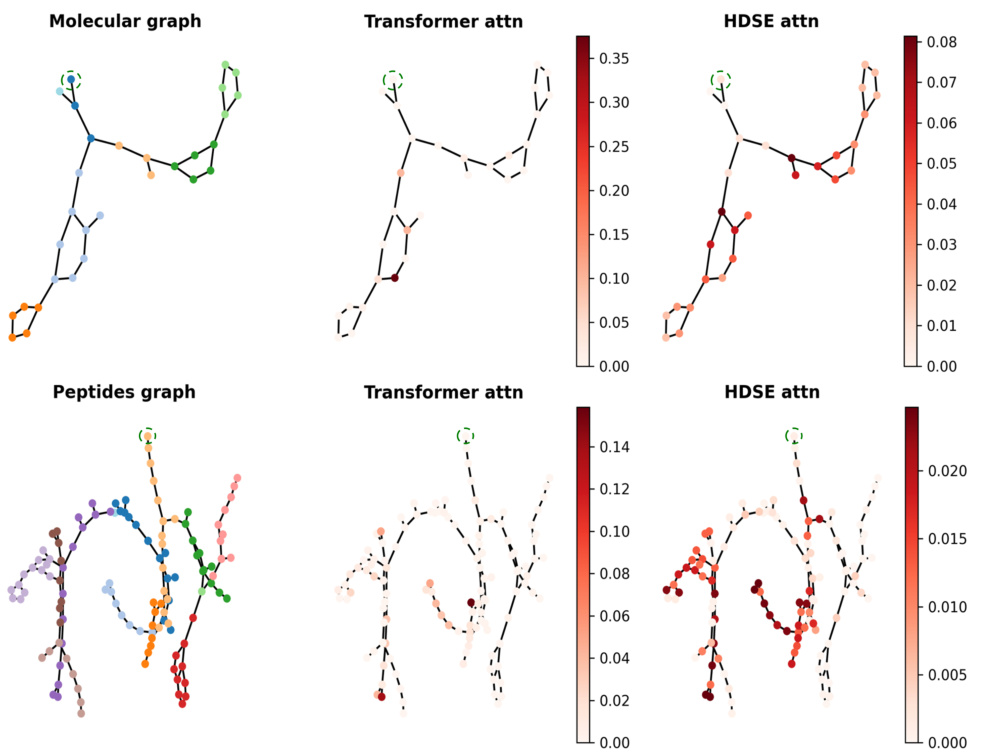
🔼 The figure visualizes attention weights learned by a classic graph transformer (GT) and the proposed HDSE-enhanced transformer. It shows how HDSE refines attention by focusing on hierarchical structures within the graph, in contrast to the GT’s more dispersed attention. The left side shows the coarsening process.
read the caption
Figure 3: Visualization of attention weights for the transformer attention and HDSE attention. The left side illustrates the graph coarsening result. The center column displays the attention weights of a sample node learned by the classic GT [19], while the right column showcases the attention weights learned by the HDSE attention.
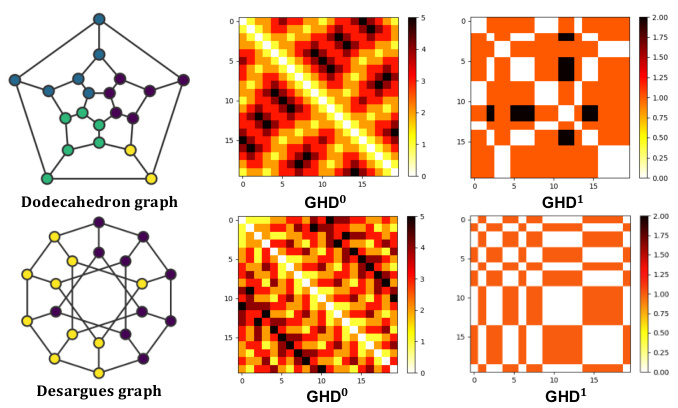
🔼 This figure visually demonstrates the capability of HDSE in capturing chemical motifs and distinguishing graphs that are indistinguishable using the GD-WL test with SPD. The left side shows how HDSE, utilizing graph coarsening, identifies chemical motifs (CF3 and aromatic rings) in molecule graphs, highlighting the hierarchical nature of the structural information captured. The right side illustrates the effectiveness of HDSE in distinguishing the Dodecahedron and Desargues graphs, which are known to be challenging for traditional methods like GD-WL with SPD.
read the caption
Figure 2: Examples of graph coarsening results and hierarchy distances. Left: HDSE can capture chemical motifs such as CF3 and aromatic rings on molecule graphs. Right: HDSE can distinguish the Dodecahedron and Desargues graphs. The Dodecahedral graph has 1-level hierarchy distances of length 2 (indicated by the dark color), while the Desargues graph doesn't. In contrast, the GD-WL test with SPD cannot distinguish these graphs [89].

🔼 This figure visualizes the attention weights of the transformer attention and HDSE attention for different nodes in molecular and peptide graphs. The left side shows the graph after coarsening. The middle column shows the attention weights from the baseline Graph Transformer (GT), and the right column shows the attention weights from the GT model with HDSE. The visualizations illustrate that HDSE helps the model focus its attention on relevant parts of the graph with multi-level hierarchical structures, rather than uniformly across all nodes like in the baseline GT.
read the caption
Figure 5: Visualization of attention weights for the transformer attention and HDSE attention. The left side illustrates the graph coarsening result. The center column displays the attention weights of a randomly sample node (enclosed in a green dashed box) learned by the classic GT, while the right column showcases the attention weights learned by the HDSE attention. Note that different randomly selected nodes consistently demonstrate the ability to capture a multi-level hierarchical structure.
More on tables
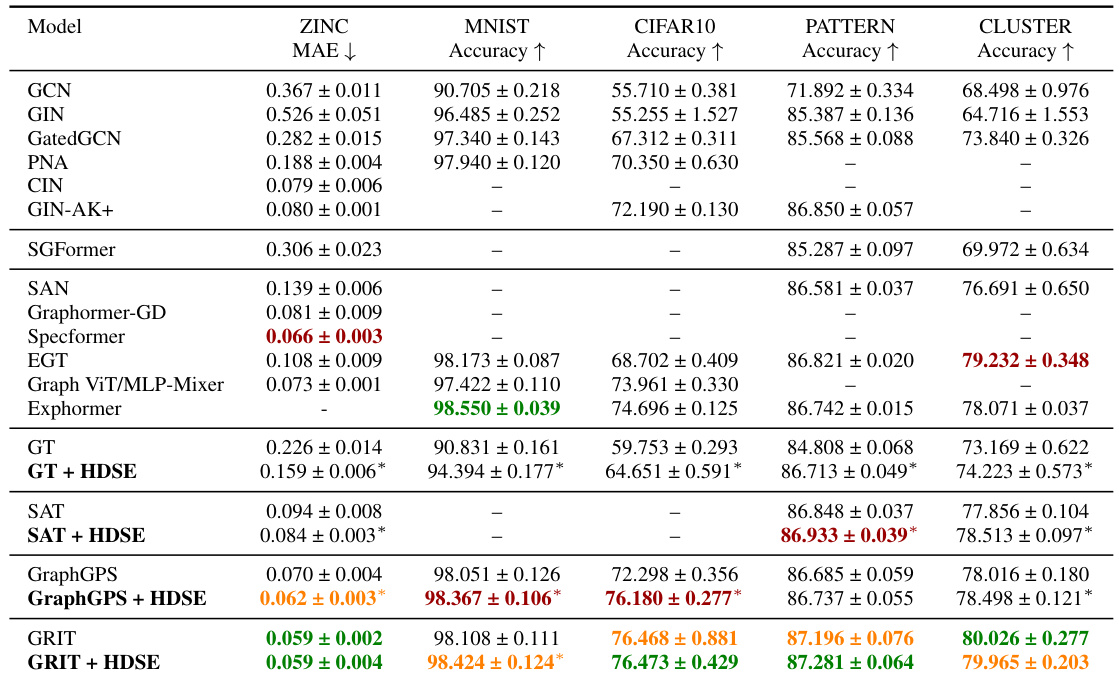
🔼 This table presents the test performance results on five graph-level benchmark datasets from the Benchmarking GNNs paper [20]. It compares the performance of several graph transformer models, both with and without the proposed HDSE method. The results, averaged over five runs with different random seeds, show the Mean Absolute Error (MAE) for regression tasks and accuracy for classification tasks. Statistically significant improvements (p<0.05) achieved by HDSE are marked with an asterisk (*). The top three performing models for each dataset are highlighted.
read the caption
Table 2: Test performance in five benchmarks from [20]. The results are presented as the mean ± standard deviation from 5 runs using different random seeds. Baseline results were obtained from their respective original papers. * indicates a statistically significant difference against the baseline w/o HDSE from the one-tailed t-test. Highlighted are the top first, second and third results.
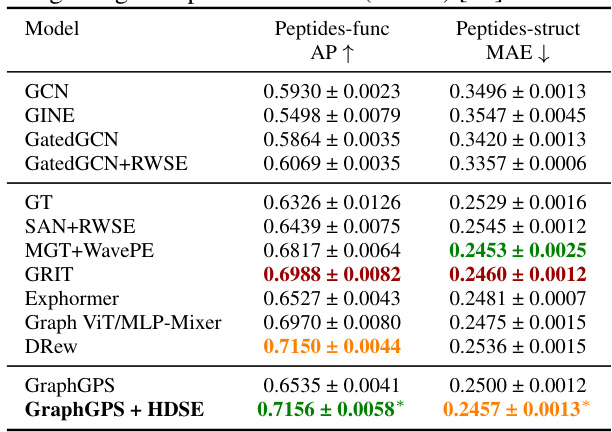
🔼 This table presents the results of the proposed method and several baselines on two peptide datasets from the Long Range Graph Benchmark. The metrics used are Average Precision (AP) for the Peptides-func dataset and Mean Absolute Error (MAE) for the Peptides-struct dataset. The table highlights the improved performance of the proposed method (GraphGPS + HDSE) compared to other methods.
read the caption
Table 3: Test performance on two peptide datasets from Long-Range Graph Benchmarks (LRGB) [23].

🔼 This table presents the ablation study results on the ZINC dataset using different graph coarsening algorithms. It compares the Mean Absolute Error (MAE) achieved by the SAT and GraphGPS models when combined with HDSE using various coarsening algorithms (METIS, Spectral, Loukas, Newman, Louvain). The ‘w/o’ row shows the baseline MAE without using any coarsening algorithm. This helps determine the best-performing coarsening technique for enhancing the accuracy of graph transformers with HDSE on the ZINC dataset.
read the caption
Table 4: Ablation experiments of coarsening algorithms on ZINC.
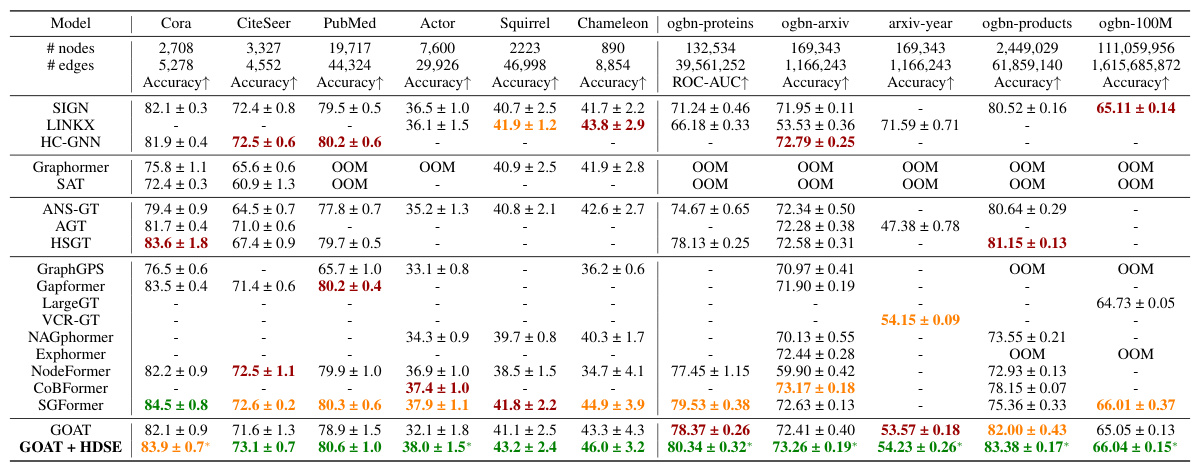
🔼 This table presents the results of node classification experiments on eleven large-scale graph datasets. The table compares the performance of the proposed HDSE method (GOAT + HDSE) against various state-of-the-art graph neural networks (GNNs) and graph transformers. The results are presented as accuracy percentages, with standard deviations from multiple runs. The table also notes instances where models ran out of memory (OOM) during training due to the size of the datasets.
read the caption
Table 5: Node classification on large-scale graphs (%). The baseline results were primarily taken from [82], with the remaining obtained from their respective original papers. OOM indicates out-of-memory when training on a GPU with 24GB memory.

🔼 This table compares the training time per epoch for three different graph transformer models: NodeFormer, SGFormer, and GOAT+HDSE. The comparison is done across five different large-scale graph datasets: PubMed, ogbn-proteins, ogbn-arxiv, ogbn-products, and ogbn-papers100M. The results show that GOAT+HDSE achieves significantly faster training times compared to the other two models, highlighting its efficiency for large-scale graph processing.
read the caption
Table 6: Efficiency comparison of GOAT + HDSE and scalable graph transformer competitors; training time per epoch.

🔼 This ablation study investigates the impact of removing the high-level HDSE and replacing the coarsening projection matrix with the original projection matrix used in GOAT, demonstrating the contributions of each component to the model’s performance across three datasets: Actor, ogbn-proteins, and arxiv-year.
read the caption
Table 7: Ablation study of GOAT + HDSE. 'w/o coarsening' refers to replacing the projection matrix with the original projection matrix used in GOAT.
🔼 This table presents the test performance results on five benchmark datasets from the Benchmarking GNNs paper [20]. The results are shown as mean ± standard deviation, obtained from five independent runs using different random seeds. For comparison, baseline results from the original papers are also included. A one-tailed t-test was used to determine statistical significance between the results with and without HDSE. The top three performing models for each metric are highlighted.
read the caption
Table 2: Test performance in five benchmarks from [20]. The results are presented as the mean ± standard deviation from 5 runs using different random seeds. Baseline results were obtained from their respective original papers. * indicates a statistically significant difference against the baseline w/o HDSE from the one-tailed t-test. Highlighted are the top first, second and third results.

🔼 This table presents the hyperparameters used for training the GraphGPS model enhanced with HDSE on five benchmark datasets from the Benchmarking GNNs paper [20]. The hyperparameters shown include the number of GPS layers, hidden dimension, type of GPS-MPNN and GPS-GlobAttn modules, the number of heads, attention dropout rate, graph pooling method, positional encoding type and dimension, positional encoding generation method, batch size, learning rate, number of epochs, number of warmup epochs, weight decay, maximum hierarchy level K, coarsening algorithm, and the total number of parameters. These settings are dataset-specific, and the details for each dataset are provided in separate rows.
read the caption
Table 9: Hyperparameters of GraphGPS + HDSE for five datasets from [20].

🔼 This table lists the hyperparameters used for the GraphGPS + HDSE model on five benchmark datasets from the Benchmarking GNNs paper [20]. The hyperparameters include details about the number of GPS layers, hidden dimension, the type of MPNN and global attention used, the number of heads in the attention mechanism, the attention dropout rate, the type of graph pooling used, the type of positional encoding, the dimension of the positional encoding, the positional encoding encoder, the batch size, the learning rate, the number of epochs, the number of warmup epochs, the weight decay, the maximum hierarchy level (K), the coarsening algorithm used, and the total number of parameters. Each dataset has a slightly different set of hyperparameters to optimize performance.
read the caption
Table 9: Hyperparameters of GraphGPS + HDSE for five datasets from [20].

🔼 This table lists the hyperparameters used for the GOAT + HDSE model on various datasets. It shows how the hyperparameters, such as the number of layers, hidden dimension, number of heads, and learning rate, were adjusted based on the characteristics of each dataset. The table also indicates the type of local GNN used (GCN or GraphSAGE) and the number of GNN layers for each dataset.
read the caption
Table 11: GOAT + HDSE dataset-specific hyperparameter settings.
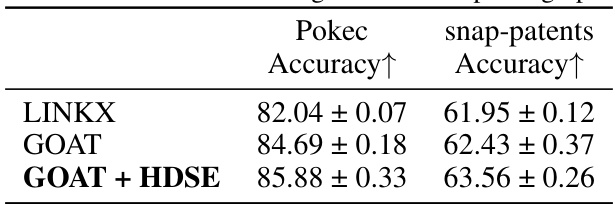
🔼 This table presents the results of node classification experiments conducted on two large-scale heterophilic graph datasets: Pokec and snap-patents. The accuracy is reported for three different models: LINKX (a baseline model), GOAT (a graph transformer model), and GOAT + HDSE (the proposed model that integrates Hierarchical Distance Structural Encoding). The results demonstrate the superior performance of GOAT + HDSE compared to the baseline models on both datasets, indicating the effectiveness of the HDSE method in handling heterophilic graphs.
read the caption
Table 12: Performance on large-scale heterophilic graphs.

🔼 This table presents the results of a sensitivity analysis conducted to determine the optimal value for the maximum hierarchy level (K) in the GraphGPS + HDSE model. The analysis was performed on the ZINC dataset, evaluating the Mean Absolute Error (MAE) for different values of K (0, 1, and 2). K=0 represents using only the shortest path distance (SPD), while K=1 and K=2 represent incorporating hierarchical distances at different levels. The results indicate the impact of incorporating hierarchical information on model performance.
read the caption
Table 13: Sensitivity analysis on the maximum hierarchy level K of GraphGPS + HDSE on ZINC.
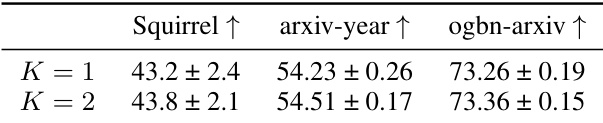
🔼 This table presents the results of a sensitivity analysis conducted to determine the optimal maximum hierarchy level (K) for the GOAT + HDSE model. The analysis was performed on three large-scale graph datasets: Squirrel, arxiv-year, and ogbn-arxiv. The table shows the accuracy achieved for each dataset with K values of 1 and 2. The results help in identifying the best value of K that balances model performance and complexity.
read the caption
Table 14: Sensitivity analysis on the maximum hierarchy level K of GOAT + HDSE.

🔼 This table presents the average and maximum graph diameters for seven datasets used in the graph classification experiments. The datasets include ZINC, MNIST, CIFAR10, PATTERN, CLUSTER, Peptides-func, and Peptides-struct. The diameter is a measure of the longest shortest path between any two nodes in a graph. The values illustrate the range of graph sizes and complexities considered in the study. This information is useful in understanding the scope and challenges of the graph classification task and in selecting appropriate values for hyperparameters like maximum distance length (L) in the HDSE method.
read the caption
Table 15: Overview of the graph diameters of datasets used in graph classification

🔼 This table presents the results of the graph classification and regression tasks on two peptide datasets from the Long Range Graph Benchmark [23]. The table compares the performance of GraphGPS, a state-of-the-art graph transformer, with and without HDSE (Hierarchical Distance Structural Encoding). The results show the Average Precision (AP) for the Peptides-func dataset and the Mean Absolute Error (MAE) for the Peptides-struct dataset. The comparison highlights the improvement in performance achieved by incorporating HDSE into the GraphGPS model.
read the caption
Table 3: Test performance on two peptide datasets from Long-Range Graph Benchmarks (LRGB) [23].
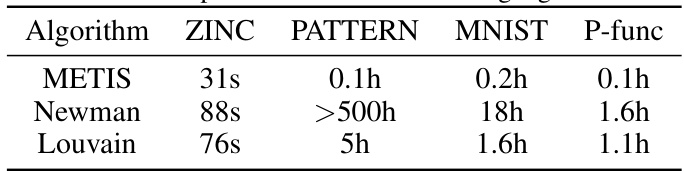
🔼 This table shows the runtime of different coarsening algorithms (including distance calculation) for four graph-level datasets: ZINC, PATTERN, MNIST, and P-func. The results highlight the efficiency of the METIS algorithm compared to Newman and Louvain, especially for larger datasets where Newman’s runtime becomes impractical. The table demonstrates the relatively low computational overhead introduced by the HDSE method itself.
read the caption
Table 17: Empirical runtime of coarsening algorithms.

🔼 This table presents the results of node classification experiments on three benchmark datasets (Cora, CiteSeer, and PubMed) using the GOAT model with and without the HDSE method. Two different linear coarsening algorithms (METIS and Loukas) are compared within the HDSE method to evaluate their impact on classification performance. The table shows the accuracy of each method on each dataset, indicating the improvement achieved by incorporating the HDSE method and highlighting the algorithm’s comparative efficiency.
read the caption
Table 18: Node classification results with linear coarsening algorithms on Cora, CiteSeer, and PubMed.

🔼 This table presents the results of node classification experiments on a synthetic dataset called ‘Community-small’, which consists of 100 graphs each having two distinct communities. The experiments compare three different methods: GT (Graph Transformer), GT + SPD (Graph Transformer with Shortest Path Distance encoding), and GT + HDSE (Graph Transformer with Hierarchical Distance Structural Encoding). The results are shown in terms of accuracy, representing the percentage of correctly classified nodes. The table highlights the superior performance of GT + HDSE compared to the other two methods, demonstrating the effectiveness of incorporating hierarchical distance information for improved node classification in graphs with community structures.
read the caption
Table 19: Node classification on synthetic community datasets.
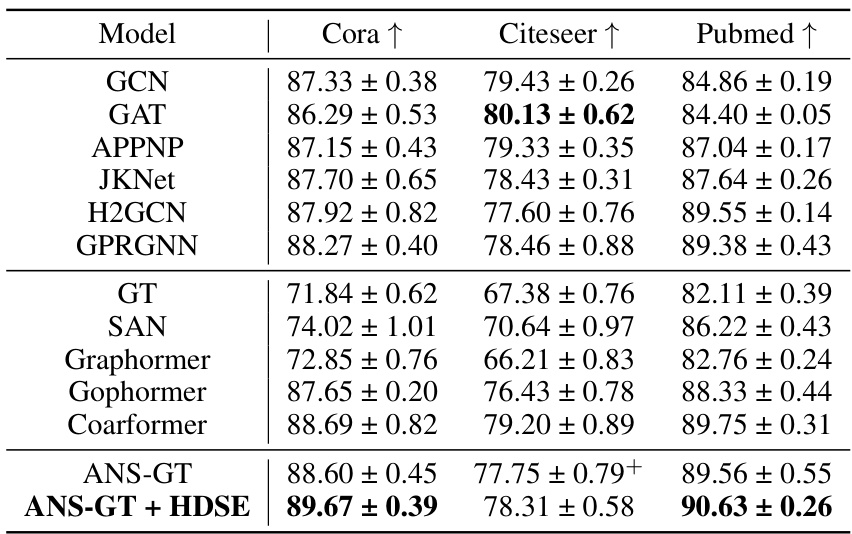
🔼 This table presents the results of node classification experiments on eleven large-scale graph datasets. It compares the performance of several methods, including the proposed HDSE method integrated into graph transformers, against various GNN baselines. The table shows accuracy scores for each model and dataset. OOM indicates that the model ran out of memory during training on a 24GB GPU.
read the caption
Table 5: Node classification on large-scale graphs (%). The baseline results were primarily taken from [82], with the remaining obtained from their respective original papers. OOM indicates out-of-memory when training on a GPU with 24GB memory.

🔼 This table presents the results of node classification experiments using the Gapformer model, both with and without the Hierarchical Distance Structural Encoding (HDSE) method. It shows the accuracy achieved on three benchmark datasets: Cora, CiteSeer, and PubMed. The comparison allows for evaluating the impact of HDSE on the Gapformer’s performance.
read the caption
Table 21: Node classification results of Gapformer with and without HDSE on Cora, CiteSeer, and PubMed.

🔼 This table presents the results of five graph-level benchmark datasets from [20] comparing the performance of several graph transformer models. The models are tested using different random seeds, and results are expressed as the mean and standard deviation of five runs. The table compares baseline models with those enhanced using the HDSE method. A * indicates where a statistically significant improvement was achieved over the baseline models.
read the caption
Table 2: Test performance in five benchmarks from [20]. The results are presented as the mean ± standard deviation from 5 runs using different random seeds. Baseline results were obtained from their respective original papers. * indicates a statistically significant difference against the baseline w/o HDSE from the one-tailed t-test. Highlighted are the top first, second and third results.
Full paper#