↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current node classification methods using graph neural networks and graph Transformers face challenges in fully utilizing graph information. Existing tokenized graph Transformers often overlook valuable information from nodes with low similarity scores, hindering optimal representation learning. This limits their ability to capture long-range dependencies within graphs, especially in datasets with heterophily (where connected nodes have dissimilar labels).
GCFormer tackles this by introducing a hybrid token generator that creates both positive and negative token sequences. This method ensures that information from diverse nodes, regardless of similarity, is incorporated. A tailored Transformer-based backbone then processes these sequences, and contrastive learning further enhances representation learning by maximizing the distinction between positive and negative sequences. Extensive experiments across various graph datasets demonstrate that GCFormer significantly improves node classification accuracy compared to state-of-the-art methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it significantly improves node classification accuracy in graph data, a critical task in various fields. By introducing contrastive learning and a novel token generation method, it addresses limitations of existing graph transformers, paving the way for more effective graph-based machine learning applications. This work is highly relevant to current research focusing on improving graph neural networks, and it opens up new avenues of research in utilizing contrastive learning and hybrid token generation techniques.
Visual Insights#
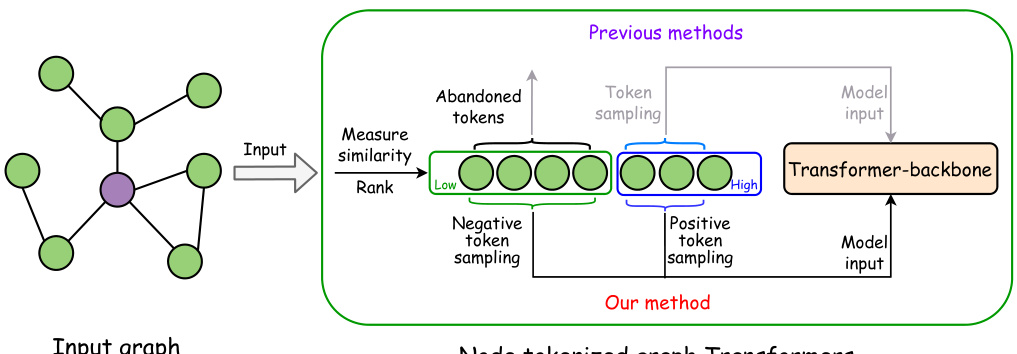
This figure illustrates the difference between previous node tokenized graph transformer methods and the proposed GCFormer method in terms of token generation. Previous methods only selected nodes with high similarity scores to the target node, ignoring other nodes. GCFormer, on the other hand, uses a hybrid token generator to create both positive (similar nodes) and negative (dissimilar nodes) token sequences, thus incorporating information from a more diverse set of nodes.
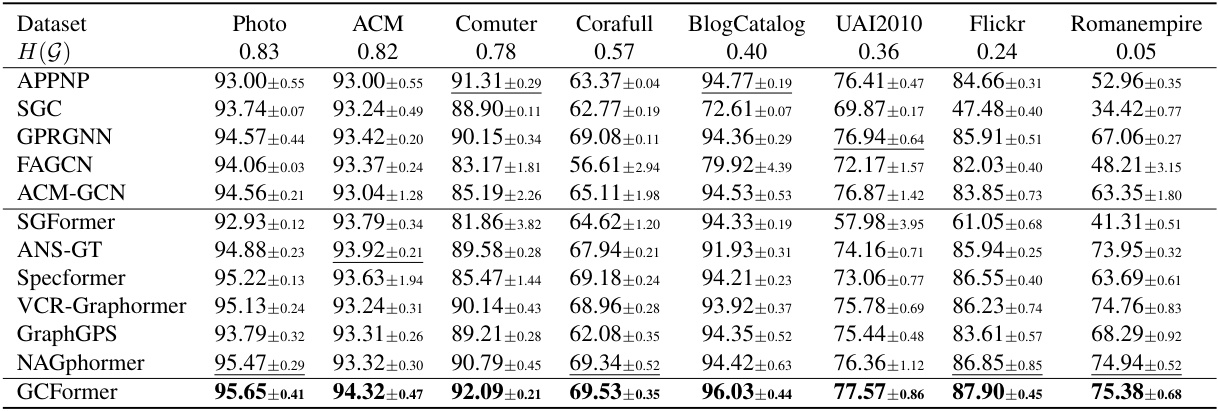
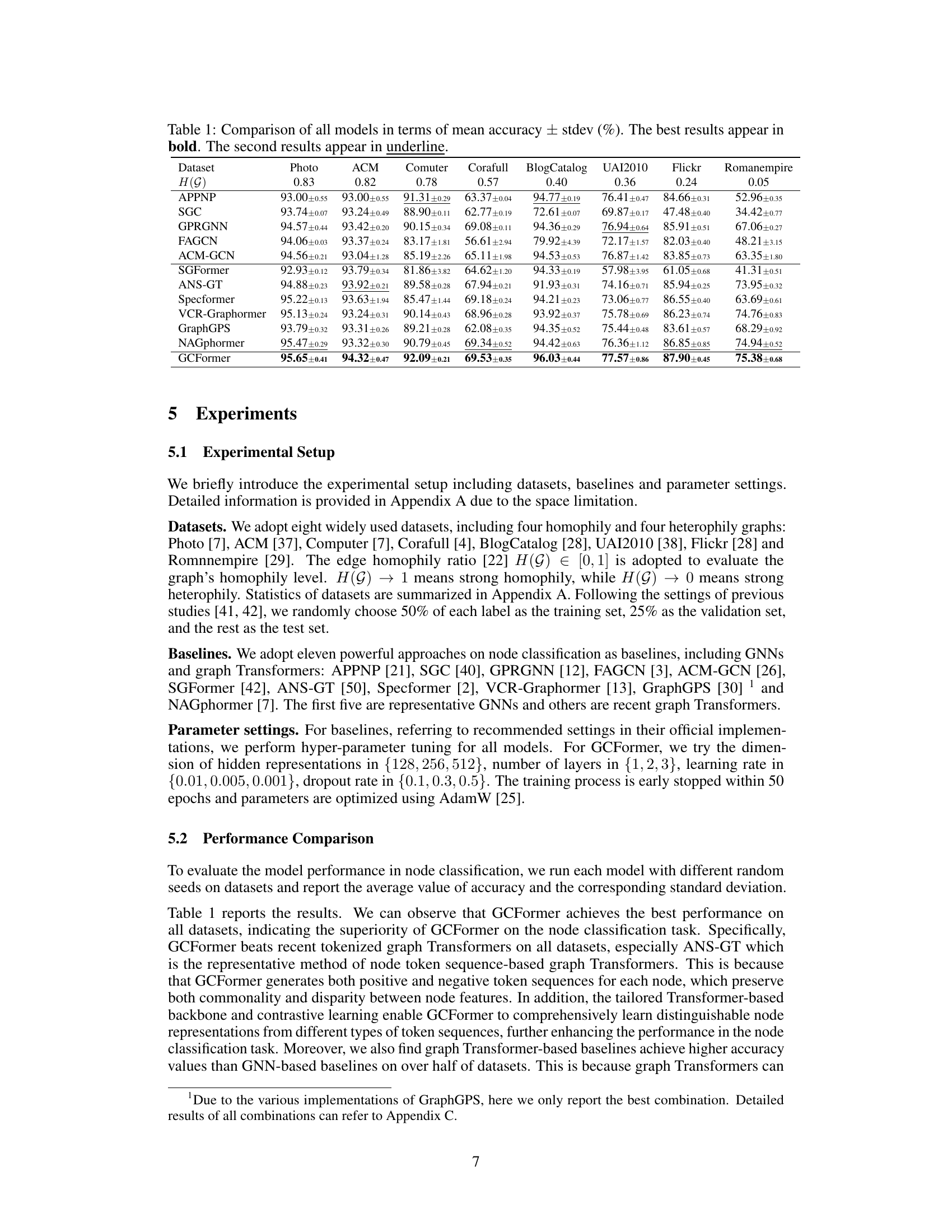
This table presents a comparison of various node classification models on eight different datasets. The models include several Graph Neural Networks (GNNs) and Graph Transformers. For each dataset and model, the table shows the mean accuracy and standard deviation. The best-performing model for each dataset is highlighted in bold, and the second-best is underlined. The datasets are categorized by their level of homophily (the tendency for similar nodes to connect).
In-depth insights#
Contrastive Node Learning#
Contrastive node learning is a powerful technique for enhancing node representations in graph neural networks. By contrasting similar and dissimilar nodes, it learns more discriminative features. This approach addresses limitations of traditional methods that struggle to capture long-range dependencies or handle heterogeneous graph structures. A key strength is its ability to leverage both positive and negative samples effectively, enriching the learning process and yielding higher-quality embeddings. The choice of negative sampling strategy is crucial, impacting the effectiveness of contrastive learning. Furthermore, integrating contrastive learning with other techniques, like graph transformers, offers even more powerful representations. However, it also introduces computational complexity, especially when dealing with large graphs. Further research is needed to optimize negative sampling techniques and explore the application of contrastive learning to various graph mining tasks.
Hybrid Token Generation#
The proposed hybrid token generator is a crucial component of the GCFormer model, designed to overcome limitations of previous tokenized graph transformers. Instead of relying solely on nodes with high similarity scores, it cleverly incorporates both positive and negative token sampling. This approach uses two types of token sequences: positive, capturing commonalities with the target node, and negative, which preserve valuable information from dissimilar nodes. This strategy enhances diversity in the input data and aids the model in learning more comprehensive and distinguishable node representations. The generation process leverages both attribute-aware and topology-aware features, enhancing the richness and representation of graph structure, leading to superior performance on node classification tasks, particularly when dealing with heterophily graphs. The two-stage sampling method (positive and negative) ensures that both similar and dissimilar nodes are considered for the target node representation, addressing a key limitation of previous methods that heavily relied on similarity.
Transformer Backbone#
A Transformer backbone, within the context of a graph neural network (GNN) for node classification, is a crucial component responsible for processing the generated node token sequences. It leverages the strengths of the Transformer architecture, such as self-attention, to capture long-range dependencies and complex relationships within the graph that traditional GNNs might struggle with. The backbone’s design is tailored to effectively handle the specific type of token sequences produced by the model’s hybrid token generator; in this case, both positive and negative token sequences are fed into it. Contrastive learning is often integrated with the backbone, enabling the model to learn more discriminative node representations by comparing similarities and differences between the positive and negative token sequences. The backbone’s architecture, often consisting of multiple Transformer layers, ultimately transforms the input sequences into informative node embeddings that are used for downstream node classification tasks. The choice of architecture and hyperparameters significantly influences the model’s performance.
GCFormer:Strengths & Weakness#
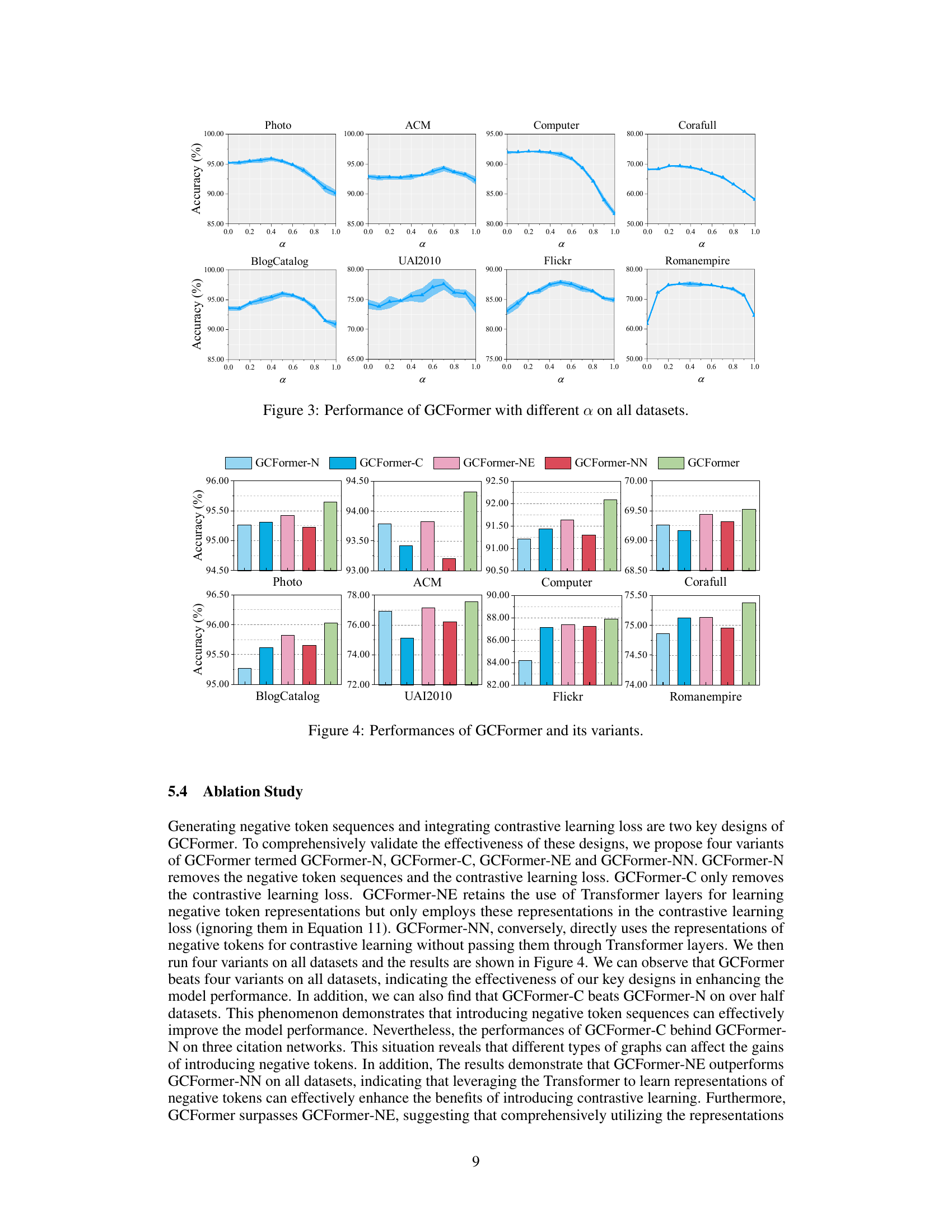
GCFormer presents several strengths. Its hybrid token generator effectively leverages both similar and dissimilar nodes, enriching node representations beyond what’s possible with methods relying solely on high-similarity tokens. The contrastive learning component further enhances these representations by explicitly modeling relationships between positive and negative tokens. GCFormer’s tailored Transformer backbone is also an advantage, allowing flexible information extraction from diverse token sequences. However, GCFormer also has weaknesses. The unified sampling strategy used for positive and negative token selection may not optimally suit all graph types; it lacks adaptability. Additionally, the parameter sensitivity analysis reveals that performance can be affected by the choices for token sampling sizes and the balance between attribute and topological features, suggesting a need for more robust parameter tuning across diverse graph structures. Finally, the computational cost associated with the extensive token generation and contrastive learning might limit scalability to extremely large graphs.
Future Research#
Future research directions stemming from this work on contrastive learning for enhanced node representations in tokenized graph transformers could explore several promising avenues. Firstly, a more sophisticated and adaptive token sampling strategy is crucial. The current approach uses a fixed sampling size, which may not be optimal for all graph types. Investigating dynamic sampling methods that adapt to the specific characteristics of each graph could significantly improve performance. Secondly, enhancing the model’s ability to handle heterophily is vital. While the current model demonstrates improvements on heterophily graphs, further research focusing on architectural modifications or incorporating alternative techniques tailored for heterophilic relationships is needed. Thirdly, exploring different contrastive learning strategies beyond the current approach could unlock additional performance gains. This could involve experimenting with different augmentation techniques or loss functions to better capture the nuanced relationships within the graph. Finally, the scalability of the model for extremely large graphs needs attention. Research into efficient implementations or approximate methods could enable the application of this approach to real-world datasets.
More visual insights#
More on figures
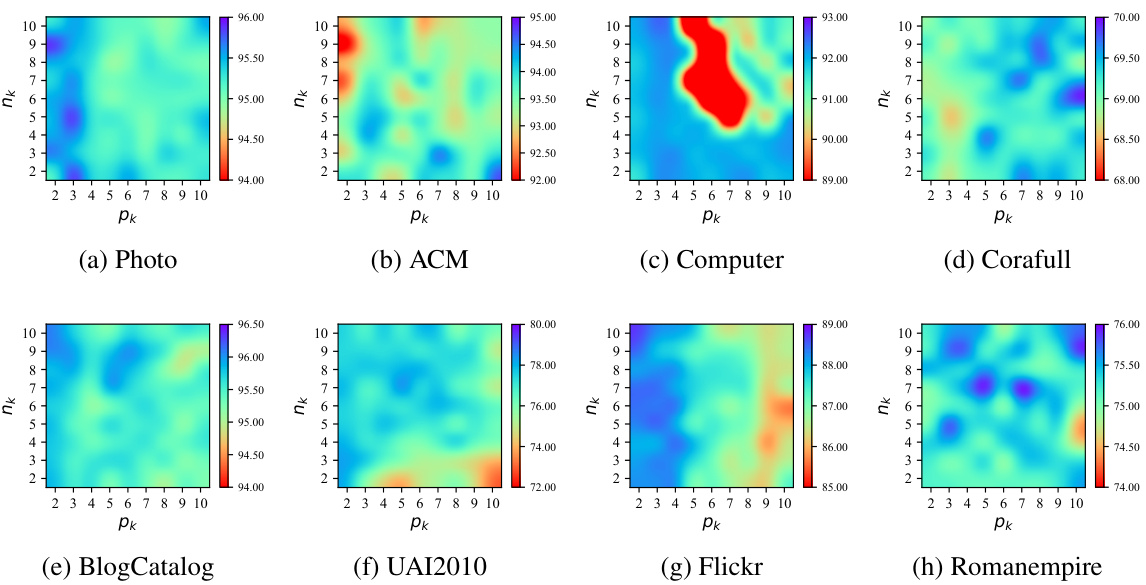
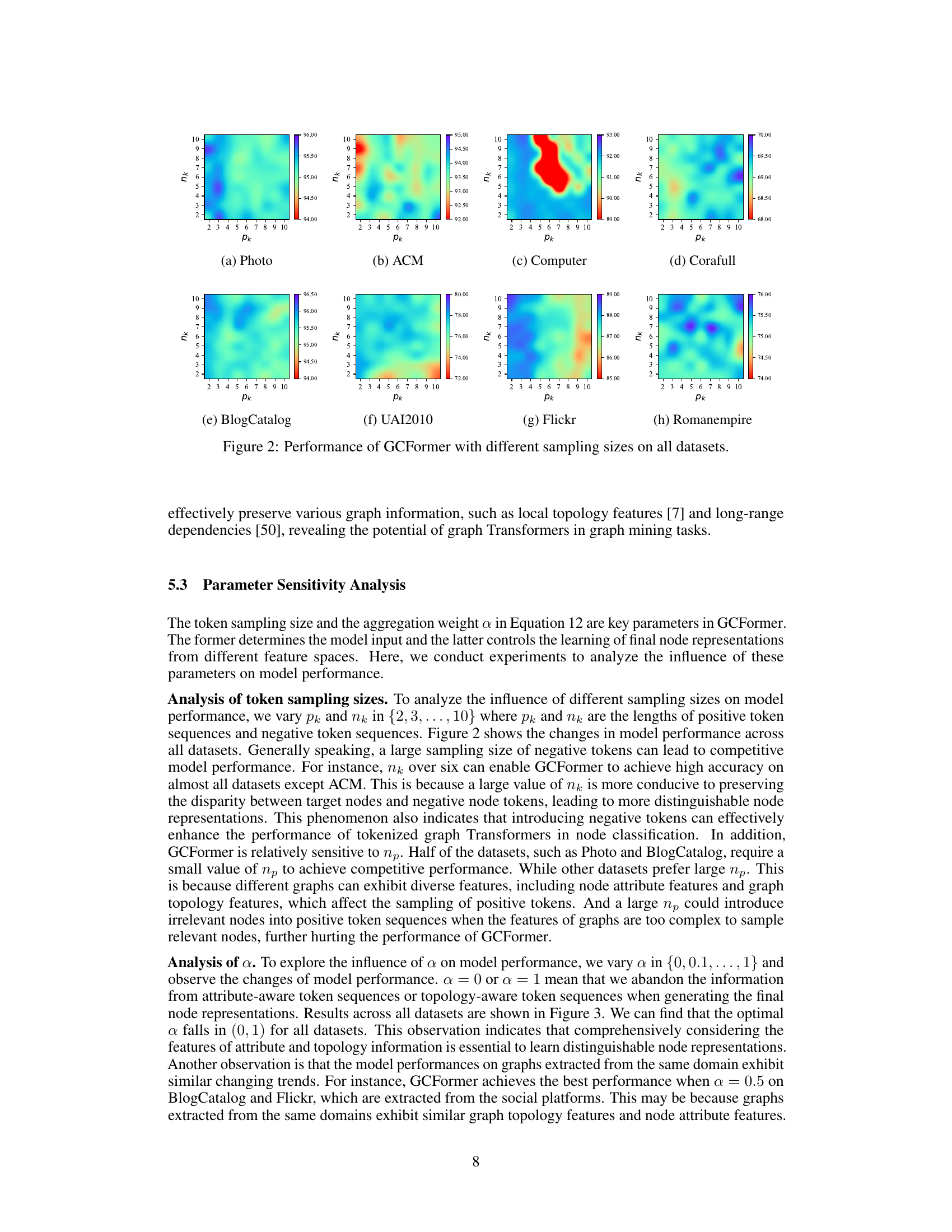
This figure shows the performance of GCFormer model with different sampling sizes (pk and nk) for both positive and negative tokens on eight datasets. The x-axis represents the size of positive tokens (pk), and the y-axis represents the size of negative tokens (nk). Each subplot corresponds to a different dataset. The color intensity represents the accuracy of the model on the specific dataset and sampling sizes.

This figure visualizes the performance of the GCFormer model across eight datasets with varying sizes of positive (pk) and negative (nk) token samples. Each subplot represents a dataset and shows how the accuracy changes with different combinations of pk and nk values. The x-axis represents pk and the y-axis represents the accuracy. The purpose is to analyze the influence of token sampling sizes on the model’s performance across different datasets and graph characteristics.

This figure displays the performance of the GCFormer model with varying sizes of positive and negative token samples. The x-axis represents the number of positive tokens (pk) and the number of negative tokens (nk). The y-axis shows the accuracy achieved on eight different datasets, categorized by homophily levels. Each subplot represents a different dataset, allowing for a visual comparison of how sample size affects performance across various graph structures. This helps demonstrate the impact of carefully selecting token sequences on model accuracy in different graph contexts.
More on tables

This table presents a comparison of the performance of various node classification models on eight different datasets. The models include both Graph Neural Networks (GNNs) and Graph Transformers. The performance metric is mean accuracy, calculated with standard deviation. The best and second-best performing models are highlighted for each dataset. The datasets vary in size, features, and level of homophily (a measure of the similarity between connected nodes).

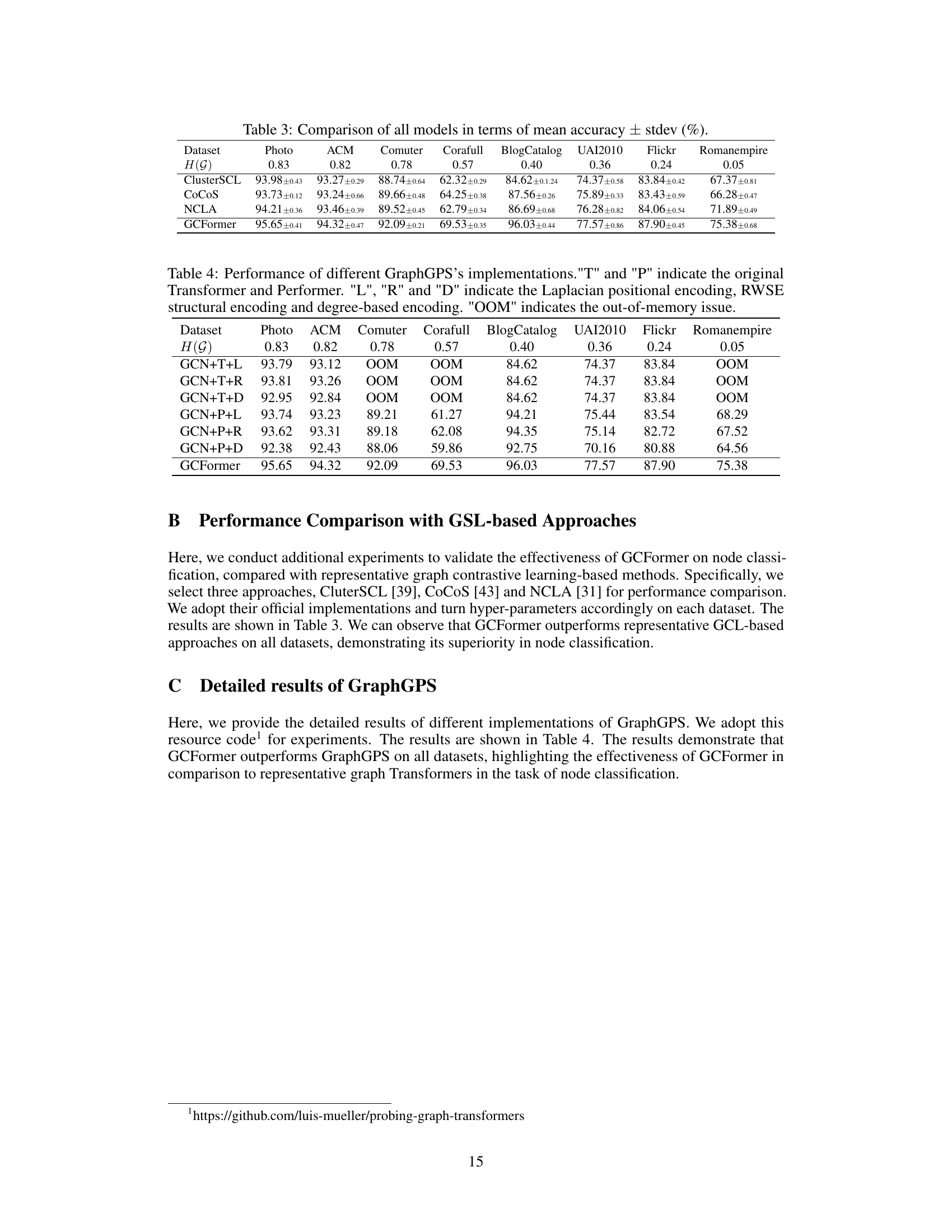
This table compares the performance of GCFormer against other state-of-the-art graph neural networks and graph transformers on eight benchmark datasets. The datasets vary in size, and the homophily level (the tendency for nodes of the same class to be connected) is also indicated. The table shows the mean accuracy and standard deviation for each model on each dataset. Bold values indicate the best-performing model on each dataset, while underlined values show the second-best performance. The results demonstrate the superiority of GCFormer in node classification.

This table compares the performance of different GraphGPS implementations on eight datasets with varying homophily levels. It shows the mean accuracy of node classification for each dataset and model variant. The variations explore different positional encoding methods combined with Transformer and Performer architectures. The ‘OOM’ indicates that the model ran out of memory on those datasets.
Full paper#