TL;DR#
Generative modeling, especially for complex data like graphs and molecules, faces challenges with existing methods. Continuous Normalizing Flows (CNFs) are powerful but computationally expensive, while diffusion-based models are limited in their sampling flexibility. Flow Matching (FM) offers efficiency but lacks flexibility. These limitations hinder the development of scalable and high-performing generative models for such data.
This paper introduces CatFlow, a novel approach to graph generation that overcomes these limitations. CatFlow leverages Variational Flow Matching (VFM), a new variational inference framework which provides a computationally efficient way to train CNFs for categorical data. The method demonstrates significantly improved performance on several benchmark graph and molecule generation tasks, exceeding the performance of existing state-of-the-art methods. The key is in parameterizing the vector field of the flow in terms of a variational approximation of the posterior probability path, leading to a highly efficient closed form objective function for categorical data.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in generative modeling, particularly those working with categorical data like graphs and molecules. CatFlow’s efficient and effective approach significantly advances the state-of-the-art in graph generation, offering a novel solution to the computational challenges of continuous normalizing flows. The variational framework introduced opens up exciting new avenues for research into both deterministic and stochastic generative models. Its superior performance and theoretical contributions make it highly relevant to current research trends and stimulate further investigations into flexible generative models for various data types.
Visual Insights#
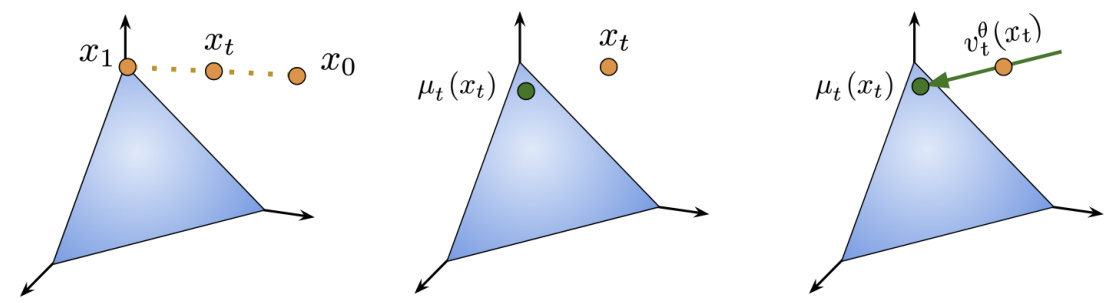
🔼 This figure illustrates how CatFlow parameterizes the vector field. Starting from an interpolant point xt between x0 and x1, CatFlow predicts a categorical distribution over possible end points x1. This distribution is parameterized by a vector μt(xt), representing the expected value of x1 given xt. The vector field vf(xt) is then constructed to ensure the trajectory converges to a point on the probability simplex at time t=1. This approach ensures that generated samples remain within the valid probability space.
read the caption
Figure 1: Parameterization of the vector field in CatFlow. Given an interpolant xt = tx1 + (1 − t)x0, CatFlow predicts a categorical distribution qf (x1 | xt) parameterized by a vector μt(xt). The resulting construction for the vector field vf (xt) = (μt(xt) − xt)/(1 − t) ensures that trajectories converge to a point on the simplex at t = 1.
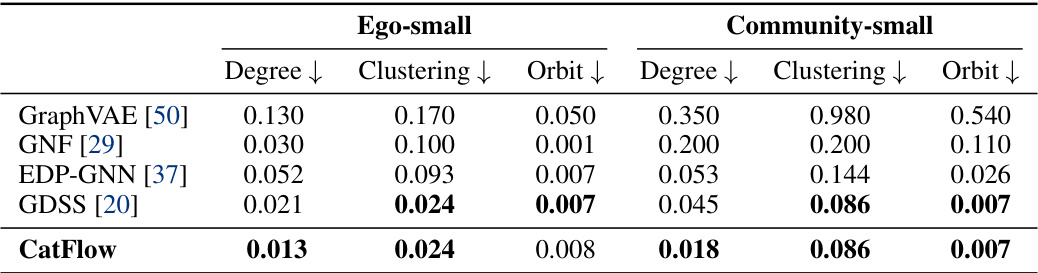
🔼 This table presents the results of the abstract graph generation task. It compares the performance of CatFlow against existing state-of-the-art methods (GraphVAE, GNF, EDP-GNN, GDSS) on two datasets: Ego-small and Community-small. The metrics used for comparison are Degree, Clustering, and Orbit, reflecting topological properties of the generated graphs. Lower values indicate better performance.
read the caption
Table 1: Results abstract graph generation.
In-depth insights#
Variational FlowMatch#
Variational Flow Matching presents a novel framework for generative modeling, particularly advantageous for categorical data like graphs. The core idea is to view flow matching through the lens of variational inference, parameterizing the vector field of the flow as an expectation over a variational distribution of possible trajectory endpoints. This approach, unlike traditional flow matching, bypasses computationally expensive ODE solving during training. By minimizing the KL divergence between the true and variational posterior distributions over endpoints, the method approximates the optimal vector field efficiently. This variational perspective allows for flexible approximation, including a fully-factorized approach simplifying computation, notably in the CatFlow implementation designed for graph generation. The CatFlow algorithm achieves strong empirical results on various graph generation benchmarks and offers a theoretical connection to score-based models, bridging deterministic and stochastic dynamics within a unified framework.
CatFlow Algorithm#
The CatFlow algorithm, presented as a novel approach to graph generation, leverages variational flow matching (VFM). VFM provides a flexible and efficient framework by parameterizing the flow’s vector field using a variational approximation of the posterior probability path. This clever reformulation allows CatFlow to overcome computational challenges associated with traditional flow matching, particularly for categorical data like graphs. CatFlow’s key strength lies in its ability to efficiently handle categorical variables, achieving this by decomposing the marginal vector field into easily computable components. This decomposition enables CatFlow to utilize a fully-factorized variational approximation without a loss of generality, resulting in a closed-form objective function expressed as a simple cross-entropy loss. The resulting model is computationally efficient and avoids the need for simulation-based training, traits especially advantageous when dealing with complex graph structures. Evaluations on diverse graph generation tasks demonstrate that CatFlow’s performance matches or surpasses existing state-of-the-art methods, highlighting the algorithm’s effectiveness and potential for broader applications in generative modeling of discrete data.
Graph Generation#
The research paper explores graph generation using a novel approach called Variational Flow Matching (VFM). VFM frames flow matching as variational inference, offering a more flexible and theoretically grounded method for learning continuous normalizing flows (CNFs). The authors introduce CatFlow, a VFM instantiation particularly well-suited for categorical data, such as graphs. CatFlow’s efficiency stems from its ability to parameterize the vector field of the flow using a variational approximation of the posterior probability path, avoiding computationally expensive ODE solvers found in other CNF training methods. The results demonstrate that CatFlow achieves strong performance on various graph generation tasks, outperforming or matching state-of-the-art methods on abstract graph generation and molecular generation benchmarks. The work further bridges the gap between flow matching and score-based models, demonstrating that VFM encompasses both deterministic and stochastic dynamics, providing a valuable theoretical framework for generative modeling.
Score Matching#
Score matching, within the context of generative modeling, presents a powerful technique for training generative models, particularly those based on diffusion processes. Instead of directly optimizing the likelihood, which is often intractable, score matching focuses on learning the score function (the gradient of the log-probability density). This approach leverages the fact that the score function, while often easier to estimate, contains sufficient information to generate samples from the target distribution. The strength of score matching lies in its ability to bypass the explicit computation of the probability density, a significant advantage for complex data distributions. Different methods exist for estimating the score function, each offering trade-offs between computational cost and accuracy. Furthermore, score matching has found application in various generative models, including diffusion models and energy-based models, showing efficacy in generating high-quality samples. A key challenge in score matching lies in the accuracy of score function estimation; inaccurate estimates can significantly hinder the model’s performance. Advances in score matching aim at more robust and efficient estimation techniques, extending its applicability to a broader range of generative models and datasets.
Future Work#
Future research directions stemming from this work on variational flow matching (VFM) and its application in CatFlow are plentiful. Extending VFM to other discrete data modalities beyond graphs, such as text or source code, presents a significant opportunity. This could involve adapting the categorical framework to different structural representations of such data. Furthermore, bridging the gap between deterministic and stochastic dynamics within the VFM framework is crucial. Investigating how the variational approximation of posterior probability paths can be leveraged to incorporate stochastic elements, similar to score-based diffusion models, would strengthen theoretical understanding and offer additional model flexibility. Finally, addressing scalability challenges inherent in handling large graphs is essential. Exploring techniques to reduce the computational cost associated with categorical computations, or investigating alternative approximation methods to make VFM more efficient for large-scale applications, is a primary concern for future work. The current quadratic cost associated with considering all possible edges in a graph limits the size of the graphs CatFlow can realistically handle. Addressing this scalability limitation is key to advancing the practical application of CatFlow in domains like drug discovery.
More visual insights#
More on figures

🔼 This figure shows some example molecules generated by the CatFlow model. The top row displays smaller molecules from the QM9 dataset, while the bottom row showcases larger molecules from the ZINC250k dataset. The figure visually demonstrates the model’s ability to generate diverse and chemically valid molecular structures of varying sizes and complexities.
read the caption
Figure 2: CatFlow samples of QM9 (top) and ZINC250k (bottom).

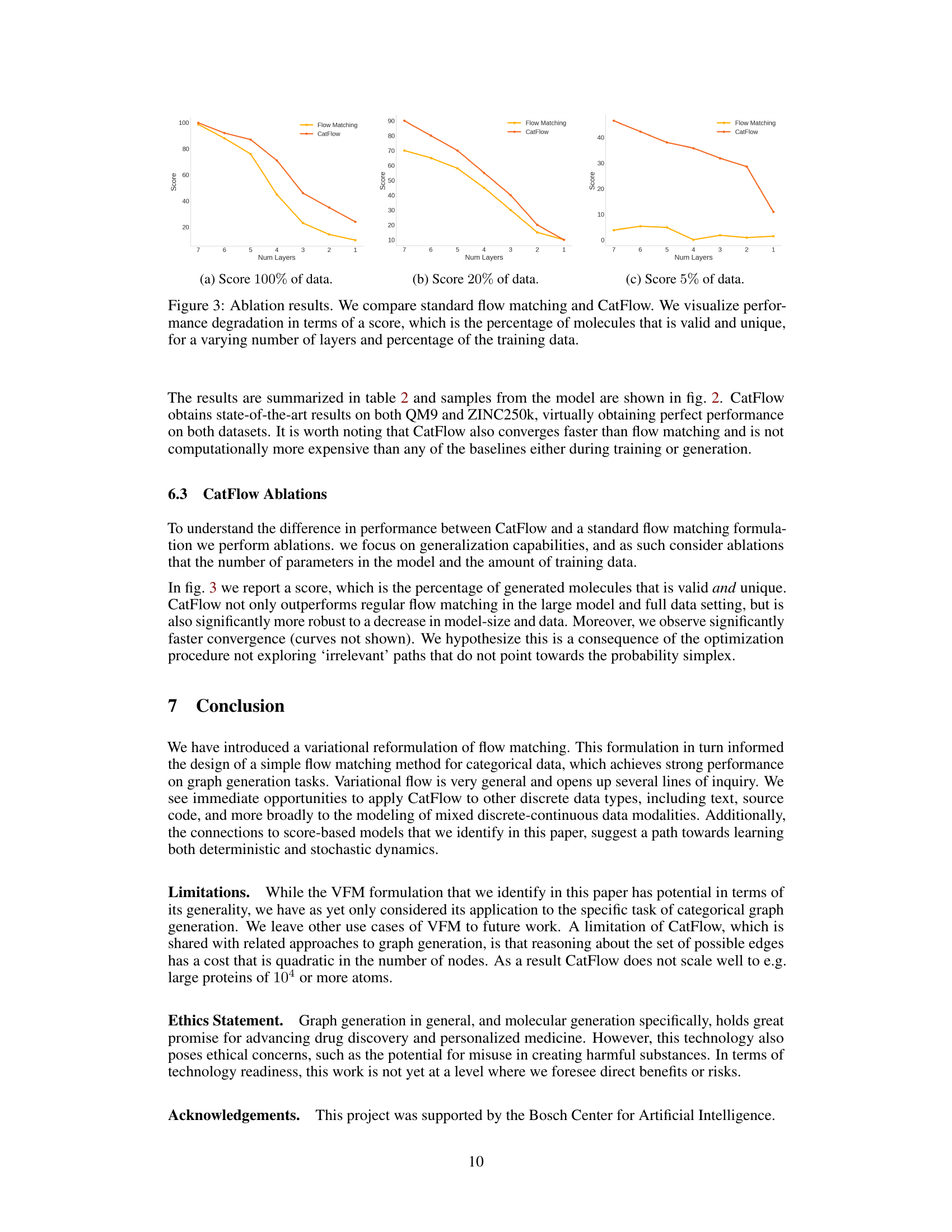
🔼 This figure shows the ablation study comparing standard flow matching and CatFlow models. The performance is measured by the ‘score’, which represents the percentage of generated molecules that are both valid and unique. The study varies the number of layers in the model and the percentage of the training data used. The results demonstrate CatFlow’s superior performance and robustness compared to standard flow matching, especially when fewer layers or less data are available.
read the caption
Figure 3: Ablation results. We compare standard flow matching and CatFlow. We visualize performance degradation in terms of a score, which is the percentage of molecules that is valid and unique, for a varying number of layers and percentage of the training data.
More on tables
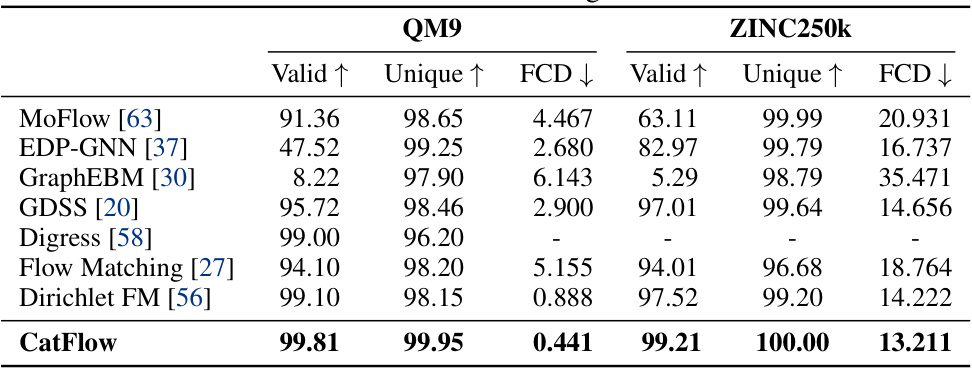
🔼 This table presents the results of molecular generation experiments using various methods, including CatFlow, on two benchmark datasets: QM9 and ZINC250k. For each method and dataset, it reports the percentage of valid molecules generated, the percentage of unique molecules, and the Fréchet ChemNet Distance (FCD). FCD is a measure of the similarity between the generated molecules and the real molecules in the dataset. Lower FCD values indicate better performance. The table demonstrates the superior performance of CatFlow compared to existing methods in terms of both validity and uniqueness of generated molecules, while achieving a comparable FCD score.
read the caption
Table 2: Results molecular generation.

🔼 This table presents the results of the abstract graph generation task. The metrics used to evaluate the performance of different models (GraphVAE, GNF, EDP-GNN, GDSS, and CatFlow) are the maximum mean discrepancy (MMD) for degree, clustering, and orbit distributions. The Ego-small and Community-small datasets are used for evaluation. Lower values indicate better performance, and CatFlow achieves the lowest values in most metrics.
read the caption
Table 1: Results abstract graph generation.

🔼 This table shows the performance of CatFlow and other state-of-the-art methods on abstract graph generation tasks. The metrics used are degree, clustering, and orbit, evaluated on two datasets: Ego-small (small ego graphs from a larger Citeseer network) and Community-small (randomly generated community graphs). Lower scores indicate better performance, suggesting that CatFlow achieves strong results, exceeding or matching the state-of-the-art.
read the caption
Table 1: Results abstract graph generation.

🔼 This table presents the results of molecular generation experiments using CatFlow on the QM9 and ZINC250k datasets. For each dataset, it shows the percentage of valid molecules generated, the percentage of unique molecules generated, and the Fréchet ChemNet Distance (FCD), which measures the similarity between the generated molecules and real molecules. Lower FCD values indicate better generation quality. CatFlow’s performance is compared to other state-of-the-art methods.
read the caption
Table 2: Results molecular generation.

🔼 This table presents the results of the abstract graph generation task. It compares the performance of CatFlow against several baselines (GraphVAE, GNF, EDP-GNN, and GDSS) across two types of graphs: Ego-small and Community-small. The metrics used for comparison include degree distribution, clustering coefficient, and orbit distribution, all assessed using the Maximum Mean Discrepancy (MMD) with Gaussian Earth Mover’s Distance kernel. Lower values for Degree, Clustering, and Orbit indicate better performance, while higher values for V.U.N. (Valid and Unique) reflect more accurate generation.
read the caption
Table 1: Results abstract graph generation.
🔼 This table presents the results of the abstract graph generation task, comparing the performance of CatFlow against other state-of-the-art methods. The metrics used to evaluate performance include degree distribution, clustering coefficient, and orbit counts for both ego-small and community-small graph datasets.
read the caption
Table 1: Results abstract graph generation.
Full paper#