↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Training large machine learning models efficiently is a major challenge, especially in distributed settings where communication bandwidth is limited. Traditional methods like stochastic gradient descent (SGD) can be slow and communication-intensive. SignSGD offers a communication-efficient alternative by transmitting only the sign of gradients, but its convergence rate can still be slow. Variance reduction techniques offer one path to improved convergence speed, but haven’t been effectively combined with SignSGD previously.
This research tackles these limitations by proposing novel sign-based algorithms incorporating variance reduction. These methods significantly improve convergence rates in both centralized (single machine) and distributed settings, handling both the standard stochastic optimization and finite-sum scenarios. The improved convergence speed is achieved through innovative variance reduction estimators combined with the use of gradient signs for parameter updates and a refined approach to majority voting in distributed settings. The effectiveness of the proposed approach is validated through extensive experimental evaluation on various machine learning tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on distributed optimization and communication-efficient algorithms. It provides novel methods to significantly speed up convergence in various settings, which is highly relevant to the ever-growing need for efficient training of large machine learning models. The proposed techniques offer improved theoretical guarantees and demonstrate practical advantages, opening new avenues for future research in this important area. The findings are relevant to both stochastic and finite-sum problems, and the methods are adaptable to heterogeneous distributed environments, expanding upon the scope of previous studies.
Visual Insights#

The figure shows the training loss, gradient norm and testing accuracy curves for different algorithms on the CIFAR-10 dataset in a centralized environment. The algorithms compared include signSGD, signSGD-SIM, SignSVRG, SSVR, and SSVR-FS. The results illustrate the convergence speed and performance of each algorithm in terms of training loss reduction, gradient norm decrease, and testing accuracy improvement. It visually compares the effectiveness of the proposed SSVR and SSVR-FS methods against existing sign-based methods.
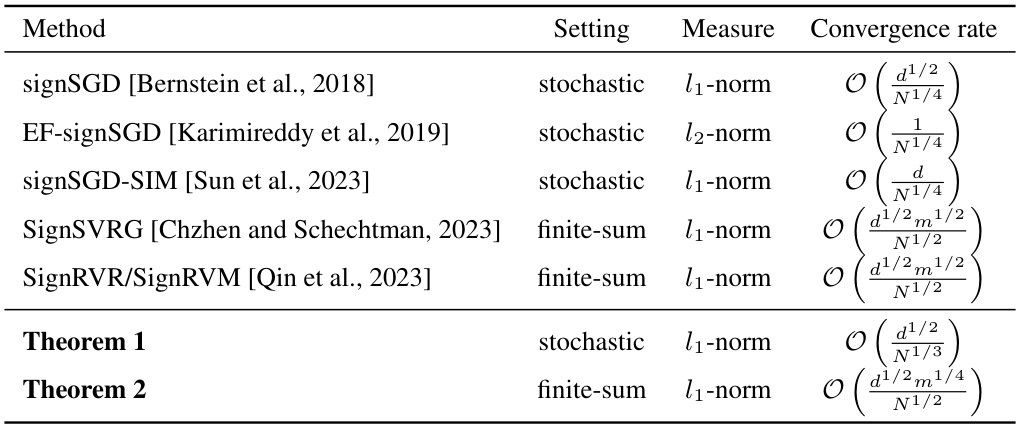
This table summarizes the convergence rates of various sign-based algorithms for both stochastic and finite-sum optimization problems. It compares the proposed methods (Theorem 1 and Theorem 2) against existing methods like signSGD, EF-signSGD, signSGD-SIM, SignSVRG, SignRVR, and SignRVM. The table shows the setting (stochastic or finite-sum), the measure (l₁-norm or l₂-norm), and the resulting convergence rate O(f(N)) in terms of the number of stochastic gradient calls (N) and the number of component functions (m) for finite-sum problems. Note that some existing results reported in the literature use the squared l₁-norm or l₂-norm, which are converted to the standard l₁-norm or l₂-norm for a fair comparison.
In-depth insights#
Sign-Based Variance#
Sign-based variance reduction methods offer a compelling approach to stochastic optimization by leveraging the sign of stochastic gradients, thereby reducing communication overhead in distributed settings and improving computational efficiency. The core idea is to estimate the true gradient using variance reduction techniques and then use only the sign of this estimate for parameter updates. This approach not only significantly reduces the communication bandwidth required but also simplifies the computation. However, it introduces a bias because the sign operation is not unbiased. Various techniques such as error feedback and momentum have been proposed to mitigate this bias. Despite the bias, sign-based methods have shown promising convergence rates, particularly when combined with variance reduction. Furthermore, the effectiveness of these methods is amplified in distributed settings, where the aggregated sign information from different nodes provides a robust and communication-efficient way to update parameters. While the theoretical convergence analysis of sign-based methods can be complex, the empirical evidence supports their ability to accelerate convergence and reduce computational cost compared to traditional methods. The performance is strongly influenced by the problem’s structure, hyperparameter settings, and the data distribution in the distributed environment. Future research directions should focus on addressing the bias inherent in the sign operation, developing more sophisticated variance reduction strategies tailored to sign-based methods, and analyzing their convergence properties under weaker assumptions.
SSVR Algorithm#
The hypothetical SSVR (Sign-based Stochastic Variance Reduction) algorithm, as described in the provided text, presents a novel approach to stochastic optimization. It leverages the efficiency of sign-based methods, transmitting only the sign of gradients, while incorporating variance reduction techniques to accelerate convergence. The core innovation lies in combining variance reduction estimators, which track gradients more accurately, with the computationally inexpensive sign operation. This balance aims to reduce both communication costs (inherent in sign-based methods) and the variance that slows SGD. The algorithm’s theoretical convergence rate improvements over standard signSGD are a significant contribution, particularly in high-dimensional settings where variance reduction is crucial. However, the effectiveness relies heavily on the assumptions made about the problem structure (average smoothness, bounded variance), and the practical performance might depend on the proper selection of hyperparameters like batch size and momentum. Further, adaptation to distributed settings via majority voting is explored, highlighting the potential for efficient parallel computation, though additional theoretical analysis and evaluation are crucial to address the potential challenges of heterogeneous environments.
Convergence Rates#
The analysis of convergence rates in optimization algorithms is crucial for understanding their efficiency. The paper investigates the convergence rate of sign-based optimization methods, which are particularly relevant for communication-efficient distributed settings. A key finding is the improvement of the convergence rate from O(d^(1/2)T^(-1/4)) to O(d^(1/2)T^(-1/3)) for non-convex stochastic problems by using a variance reduction technique. This improved rate is significant because it shows faster convergence with fewer iterations. For finite-sum problems, further enhancements are shown, achieving a rate of O(m^(1/4)d^(1/2)T^(-1/2)). The impact of heterogeneity in distributed settings is also considered. The study shows how modified algorithms can attain rates of O(d^(1/2)T^(-1/2)+dn^(-1/2)) and O(d^(1/4)T^(-1/4)), outperforming prior results. These findings underscore the effectiveness of variance reduction techniques and highlight the potential of sign-based methods in resource-constrained environments. The convergence rates are rigorously analyzed and validated through numerical experiments.
Heterogeneous Vote#
In distributed systems, a heterogeneous vote mechanism addresses the challenge of aggregating gradients from worker nodes with varying data distributions. Unlike homogeneous settings where data is uniformly distributed, heterogeneity introduces bias. A straightforward majority vote on gradient signs, as employed in some sign-based methods, can be inaccurate. The key problem is that a simple sign aggregation (e.g., summing signs then taking the sign) will not converge in a heterogeneous environment because the heterogeneity of data results in a biased majority vote. This necessitates advanced techniques like using unbiased sign estimators or variance reduction methods to improve accuracy and convergence. Variance reduction is crucial as it helps track gradients more effectively despite the data heterogeneity, leading to better estimates for aggregation. Thus, unbiased sign aggregation in conjunction with variance reduction is crucial for achieving convergence in heterogeneous distributed optimization.
Future Research#
Future research directions stemming from this work could explore extending the variance reduction techniques to other sign-based optimization methods, potentially improving their convergence rates and efficiency. Investigating the impact of different variance reduction estimators and their interplay with sign operations would also be valuable. Applying these methods to a broader range of applications, such as federated learning and distributed optimization with heterogeneous data, would offer opportunities to validate their scalability and robustness. A key area would be developing theoretical guarantees under weaker assumptions on the objective function, improving the practicality and applicability of these methods. Additionally, research into adaptive strategies for selecting parameters like learning rates and batch sizes could further enhance their performance. Finally, it would be interesting to experiment with different sign functions beyond the standard sign function, potentially uncovering new ways to balance communication efficiency with accuracy.
More visual insights#
More on figures

The figure shows the training loss and testing accuracy curves for different sign-based algorithms on the CIFAR-100 dataset in a distributed setting with 4 and 8 nodes. It compares the performance of the proposed SSVR-MV method against existing sign-based methods like signSGD, Signum, SSDM, Sto-signSGD, and MV-signSGD-SIM. The results visualize the effectiveness of the SSVR-MV method in achieving lower training loss and higher testing accuracy in both homogeneous and heterogeneous distributed learning environments.

This figure shows the training loss, gradient norm and testing accuracy for different algorithms on the CIFAR-10 dataset in a centralized setting. The algorithms compared include signSGD, signSGD-SIM, SignSVRG, SSVR, and SSVR-FS. The results show that the proposed SSVR and SSVR-FS methods achieve superior performance in terms of testing accuracy, and the SSVR algorithm outperforms other algorithms in terms of gradient norm reduction.

The figure shows the training loss, gradient norm, and testing accuracy curves for different sign-based algorithms (signSGD, signSGD-SIM, SignSVRG, SSVR, SSVR-FS) trained on the CIFAR-10 dataset in a centralized environment. The algorithms are compared to show the effectiveness of the proposed variance reduction methods (SSVR and SSVR-FS) in improving convergence and testing accuracy.

This figure compares the performance of various sign-based algorithms on the CIFAR-10 dataset in a centralized setting. It shows the training loss, gradient norm, and testing accuracy over epochs for methods such as signSGD, signSGD-SIM, SignSVRG, SSVR, and SSVR-FS. The results demonstrate the effectiveness of the proposed SSVR and SSVR-FS methods in achieving lower training loss and higher testing accuracy.

This figure shows the results of training a ResNet18 model on the CIFAR-10 dataset using various sign-based optimization algorithms in a centralized setting. The algorithms compared are signSGD, signSGD-SIM, SignSVRG, SSVR, and SSVR-FS. The plot displays the training loss and testing accuracy over 200 epochs. The purpose is to demonstrate the effectiveness of the proposed SSVR and SSVR-FS methods compared to existing sign-based methods in terms of convergence speed and testing accuracy.

The figure shows the training loss and testing accuracy curves for the CIFAR-10 dataset using the SSVR method with different momentum parameter β values (0.3, 0.5, 0.7, 0.9, 0.99). The x-axis represents the training epoch, and the y-axis shows both training loss and testing accuracy. Each line represents the average result over five different runs, with shaded regions indicating the standard deviation. The plot aims to demonstrate the impact of momentum on the convergence behavior of the SSVR algorithm and its insensitivity to variations within a certain range of β values.
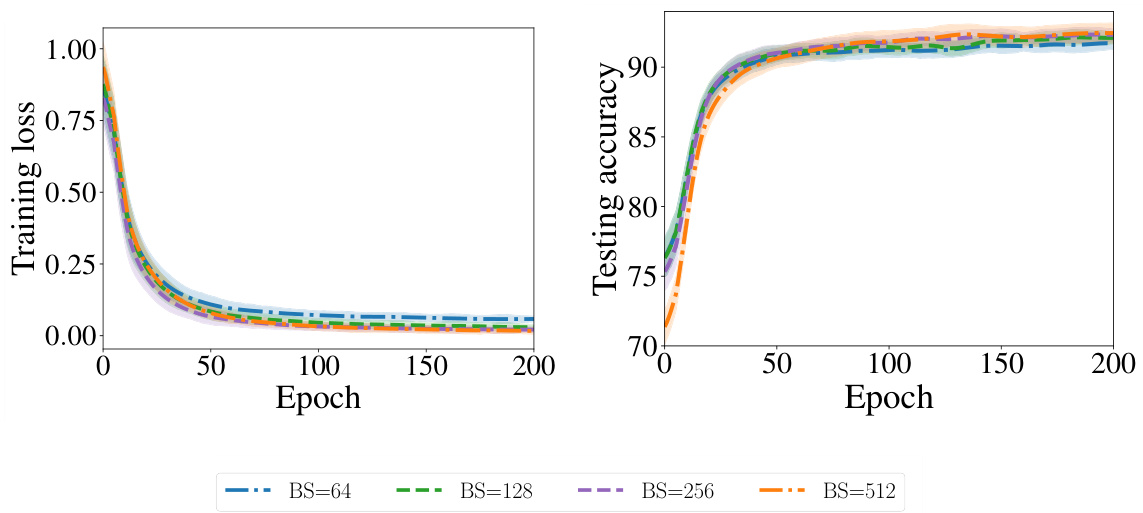
This figure shows the impact of different batch sizes (BS) on the performance of the SSVR algorithm on the CIFAR-10 dataset. The left panel displays the training loss curves, showing a similar downward trend across all batch sizes. The right panel presents the corresponding testing accuracy. While there is a slight improvement with larger batch sizes, the overall performance remains relatively consistent, suggesting that the SSVR algorithm is not highly sensitive to the choice of batch size.
Full paper#



















