↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning models require large datasets for optimal performance. However, data is often scattered across multiple owners, making aggregation challenging. This paper tackles the “dataset valuation” problem—how to fairly compensate data owners for their contributions to a joint machine learning project. The Shapley value, a game-theoretic concept, provides a theoretically sound solution but is computationally expensive to calculate. Existing approximations are often computationally costly.
This research introduces DU-Shapley, a novel approximation method that significantly improves efficiency. It leverages the inherent structure of dataset valuation to reduce the number of calculations needed. The method is proven theoretically sound with asymptotic and non-asymptotic guarantees. Experiments on both synthetic and real datasets demonstrate DU-Shapley’s significantly superior performance in terms of both accuracy and computational speed compared to existing methods. This makes it a practical tool for real-world applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on dataset valuation and cooperative game theory in machine learning. It offers a novel, efficient method for quantifying dataset contributions, addressing a major computational bottleneck in the field. This opens doors for designing better incentive mechanisms for data sharing and improving the fairness of data-driven collaborations.
Visual Insights#
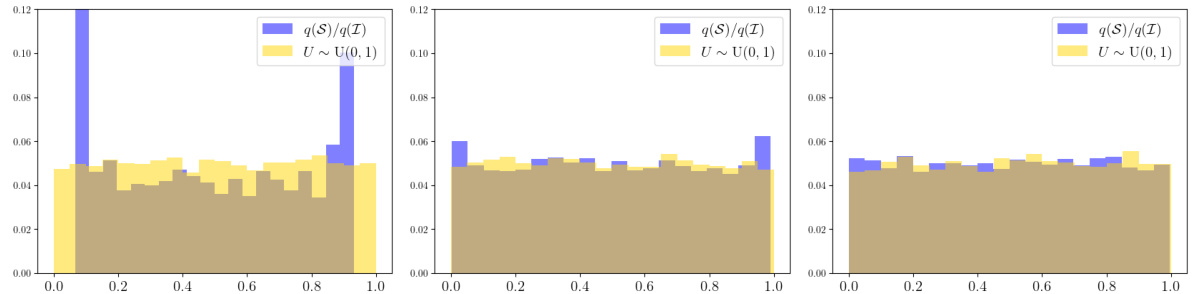
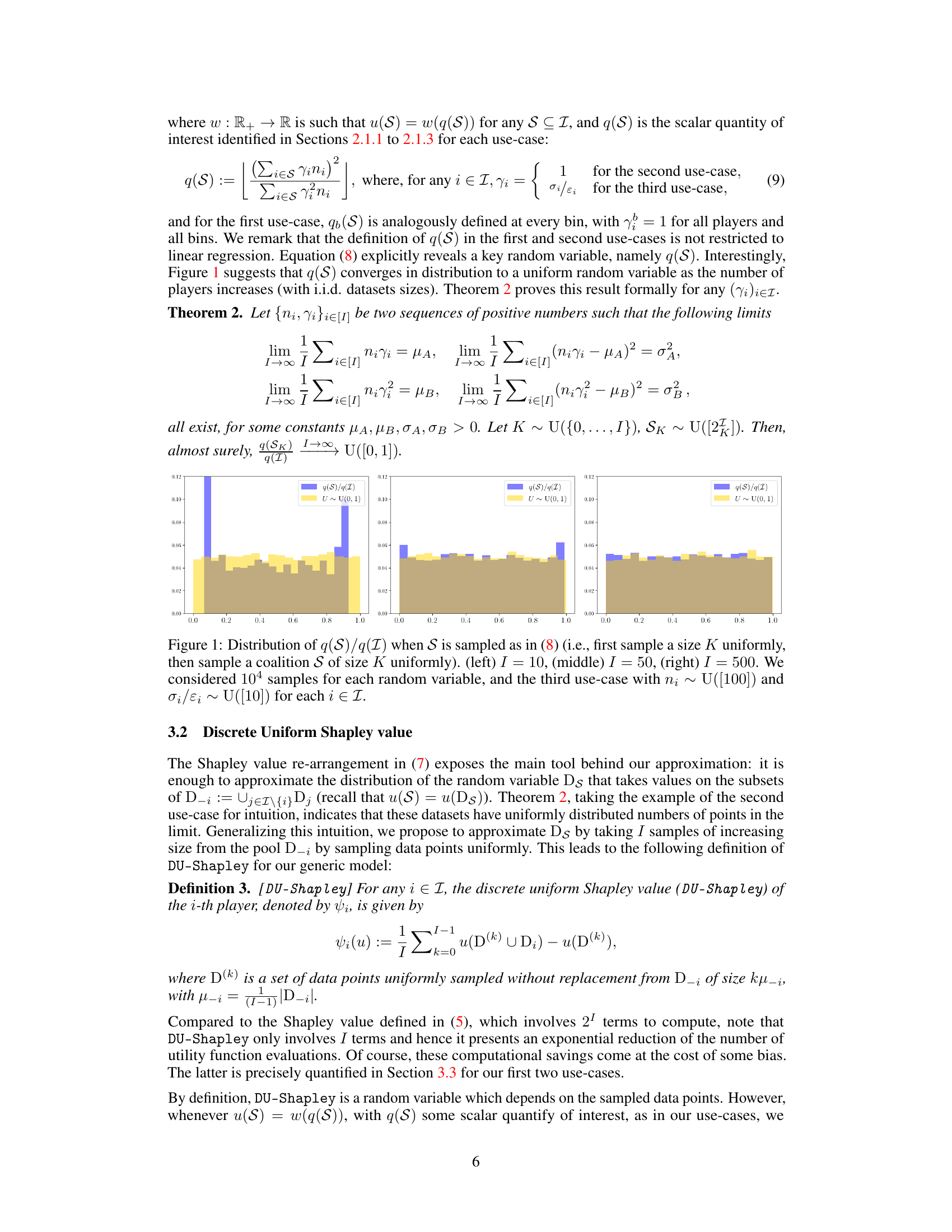
This figure displays the distribution of the ratio q(S)/q(I) obtained from sampling coalitions S of size K, where K is chosen uniformly at random from {0, …, I}. Three panels show the distribution for I = 10, I = 50, and I = 500. The data used corresponds to the third theoretical use case (heterogeneous linear regression with local differential privacy) with dataset sizes drawn uniformly from [100] and the privacy parameters drawn uniformly from [10]. The distributions are compared to the uniform distribution on [0,1], visualizing the convergence of q(S)/q(I) to a uniform distribution as the number of players (I) increases.

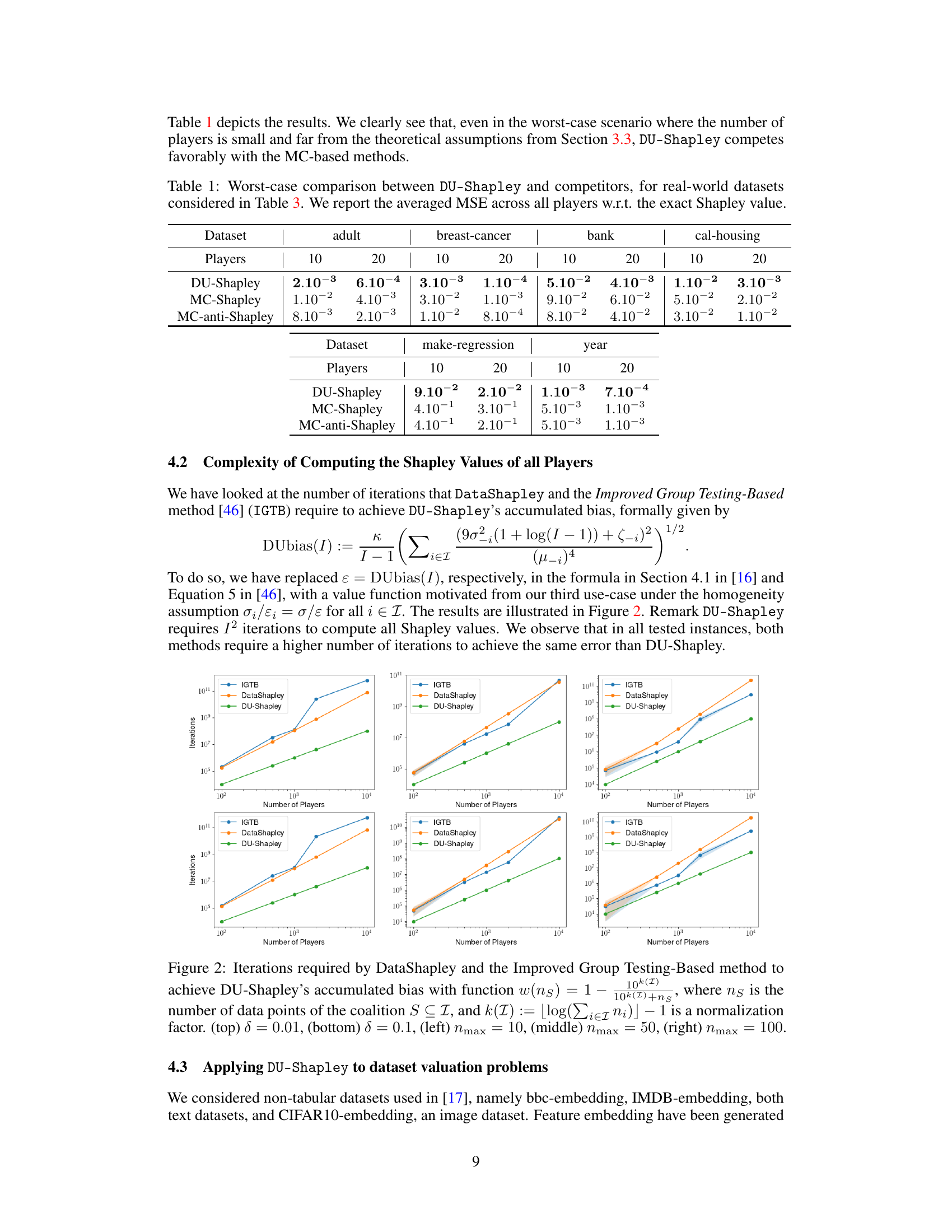
This table presents a comparison of the performance of DU-Shapley against other methods (MC-Shapley and MC-anti-Shapley) for approximating Shapley values in real-world datasets. The comparison is done in a worst-case scenario, using real-world datasets (detailed in Table 3) and with a small number of players (10 and 20). The metric used for comparison is the Mean Squared Error (MSE) averaged across all players relative to the true (exactly computed) Shapley values.
In-depth insights#
DU-Shapley Intro#
The introduction to DU-Shapley likely sets the stage by highlighting the challenge of efficiently valuing datasets within machine learning collaborations. It emphasizes the limitations of existing methods like the Shapley value, which, while theoretically sound, often prove computationally expensive. The introduction would then position DU-Shapley as a novel, efficient proxy for the Shapley value, specifically designed to address this computational bottleneck. It might mention leveraging the structure of the dataset valuation problem to create a more efficient estimator. The core of the introduction would likely highlight the key features of DU-Shapley, emphasizing its speed and scalability, achieved through a discrete uniform approximation that simplifies Shapley value calculation. Finally, the introduction may briefly mention the theoretical guarantees and empirical results validating DU-Shapley’s performance, positioning it as a significant contribution to the field of dataset valuation.
DU-Shapley Approx#
The proposed DU-Shapley approximation offers a computationally efficient alternative to the exact Shapley value calculation for dataset valuation. It leverages the structure of the dataset valuation problem, specifically focusing on the scalar quantity that captures dataset heterogeneity, rather than relying on generic Monte Carlo methods. This approach leads to an exponential reduction in the number of utility function evaluations, making it significantly faster for large datasets. Theoretical guarantees, including asymptotic convergence and non-asymptotic error bounds, support its effectiveness. The method’s performance, particularly in scenarios with numerous datasets, is highlighted by numerical experiments, showcasing significant improvements over existing MC-based approximations.
Theoretical Cases#
The theoretical cases section of the paper plays a crucial role in validating the proposed DU-Shapley method. It strategically presents three distinct use-cases to demonstrate the versatility and effectiveness of DU-Shapley under various circumstances. Each use-case is carefully selected to showcase DU-Shapley’s ability to address different challenges within the broader dataset valuation problem. These cases demonstrate how the proposed approximation method leverages the structure of the dataset valuation problem. The first use-case is non-parametric regression, demonstrating its applicability to a broad range of problems. The second use-case introduces homogeneity, simplifying the valuation and providing theoretical guarantees. Finally, the third use-case incorporates heterogeneity and local differential privacy, showcasing its robustness and adaptability in complex settings. Overall, these theoretical cases not only strengthen the paper’s theoretical foundations but also underscore the practical applicability of the proposed method in diverse real-world scenarios.
Dataset Valuation#
Dataset valuation is a crucial problem in machine learning, aiming to quantify the economic value of datasets. The Shapley value, a solution concept from cooperative game theory, offers a fair and axiomatically justified approach. However, calculating Shapley values is computationally expensive, particularly for large datasets. This paper proposes a novel approximation method, DU-Shapley, which leverages the structure of the dataset valuation problem to achieve significantly greater computational efficiency than standard methods while maintaining strong theoretical guarantees. The core idea is to approximate the Shapley value by sampling datasets uniformly, avoiding costly marginal contribution calculations. The results demonstrate that DU-Shapley excels in approximating Shapley values and accurately performs dataset valuation tasks, even under real-world conditions where strict theoretical assumptions are not met. This makes DU-Shapley a practical and effective tool for various dataset valuation applications, such as data marketplaces and collaborative data sharing initiatives.
Future Works#
The ‘Future Works’ section of a research paper on dataset valuation using the Shapley value proxy could explore several promising avenues. Extending the DU-Shapley method to handle more complex utility functions beyond those considered (non-parametric regression, homogeneous cases, and locally differentially private linear regression) is crucial for broader applicability. Investigating the impact of dataset heterogeneity and non-uniform data distributions on the accuracy and efficiency of the DU-Shapley approximation is important for real-world scenarios. Furthermore, developing more robust theoretical guarantees—especially non-asymptotic bounds—for the convergence of DU-Shapley under diverse conditions would strengthen its reliability. Exploring alternative sampling strategies to improve the efficiency of Monte Carlo methods for Shapley value estimation, while retaining theoretical guarantees, is a potential research direction. Finally, applying DU-Shapley to other multi-agent ML problems, such as feature selection, model interpretation, or federated learning, and demonstrating its benefits over existing methods, could showcase its versatility and impact.
More visual insights#
More on figures
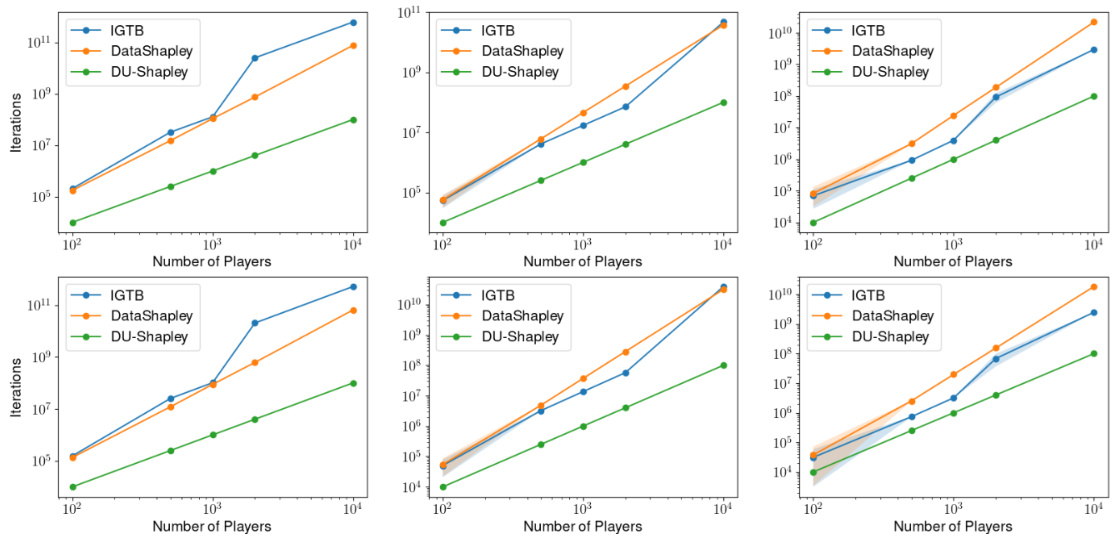
This figure compares the number of iterations needed by DataShapley and the Improved Group Testing-Based (IGTB) method to achieve the same accumulated bias as DU-Shapley. The experiment is conducted under different settings: two error tolerances (δ = 0.01 and δ = 0.1), and three maximum dataset sizes (nmax = 10, 50, and 100). The results show that DU-Shapley requires significantly fewer iterations, highlighting its computational efficiency.

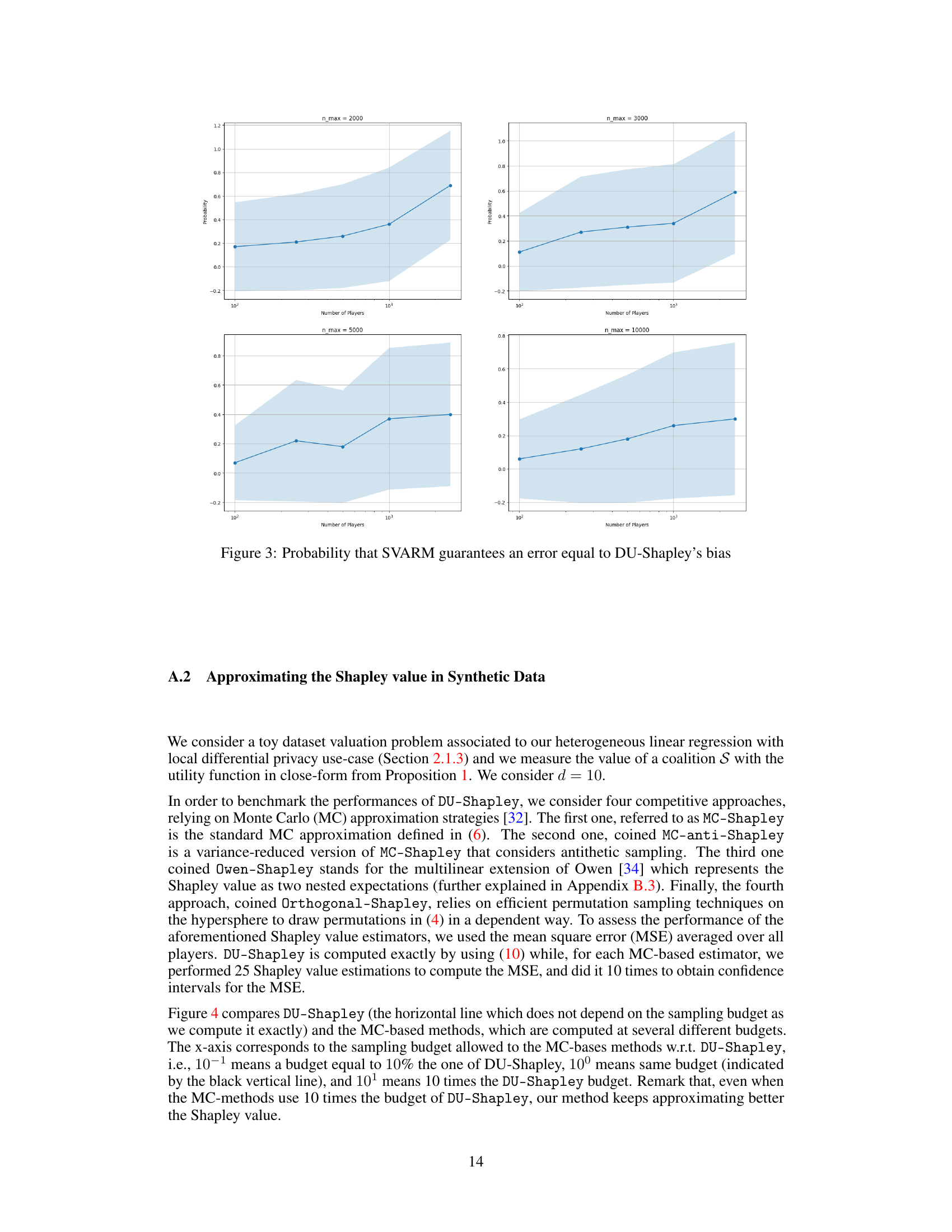
This figure shows the probability that the SVARM method achieves an error equal to or less than the bias of DU-Shapley, for different numbers of players and maximum dataset sizes (n_max). The shaded area represents the 95% confidence interval. It illustrates that as the number of players increases, the probability of SVARM matching DU-Shapley’s bias also increases. However, even with a larger number of players, the probability is not guaranteed to reach 1.

This figure compares the performance of DU-Shapley against four Monte Carlo (MC) based Shapley value approximation methods (MC-Shapley, MC-anti-Shapley, Owen-Shapley, and Ortho-Shapley) on synthetic datasets. The comparison is done across different sampling budgets relative to DU-Shapley’s budget. Two scenarios are considered: one with low heterogeneity in data variance (σi/εi ~ U([0,10])), and another with high heterogeneity (σi/εi ~ U([0,100])). The results show that DU-Shapley consistently achieves lower mean squared error (MSE) than the MC methods, even when the MC methods are given significantly larger computational budgets. The plots clearly demonstrate the superior efficiency and accuracy of the proposed DU-Shapley approach.
More on tables
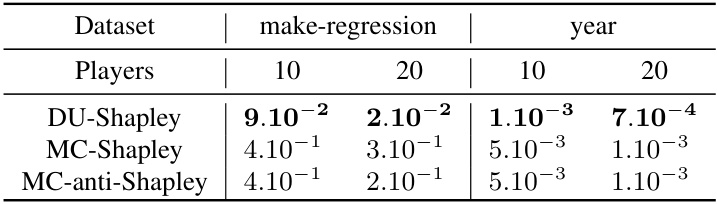
This table presents a comparison of the performance of DU-Shapley against other methods (MC-Shapley and MC-anti-Shapley) in approximating Shapley values for real-world datasets. The ‘worst-case’ scenario involves a smaller number of players (10 and 20) than is ideal for DU-Shapley’s asymptotic guarantees to fully take effect. The table reports the Mean Squared Error (MSE) averaged across all players, relative to the true Shapley value, showcasing DU-Shapley’s competitiveness even under less-than-ideal conditions.
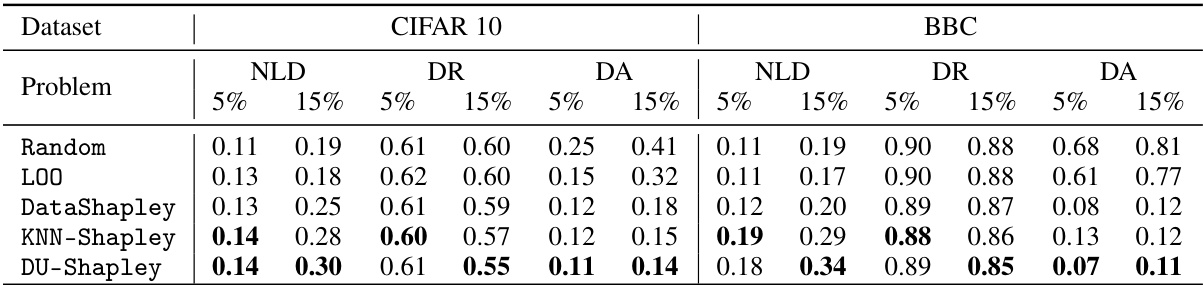
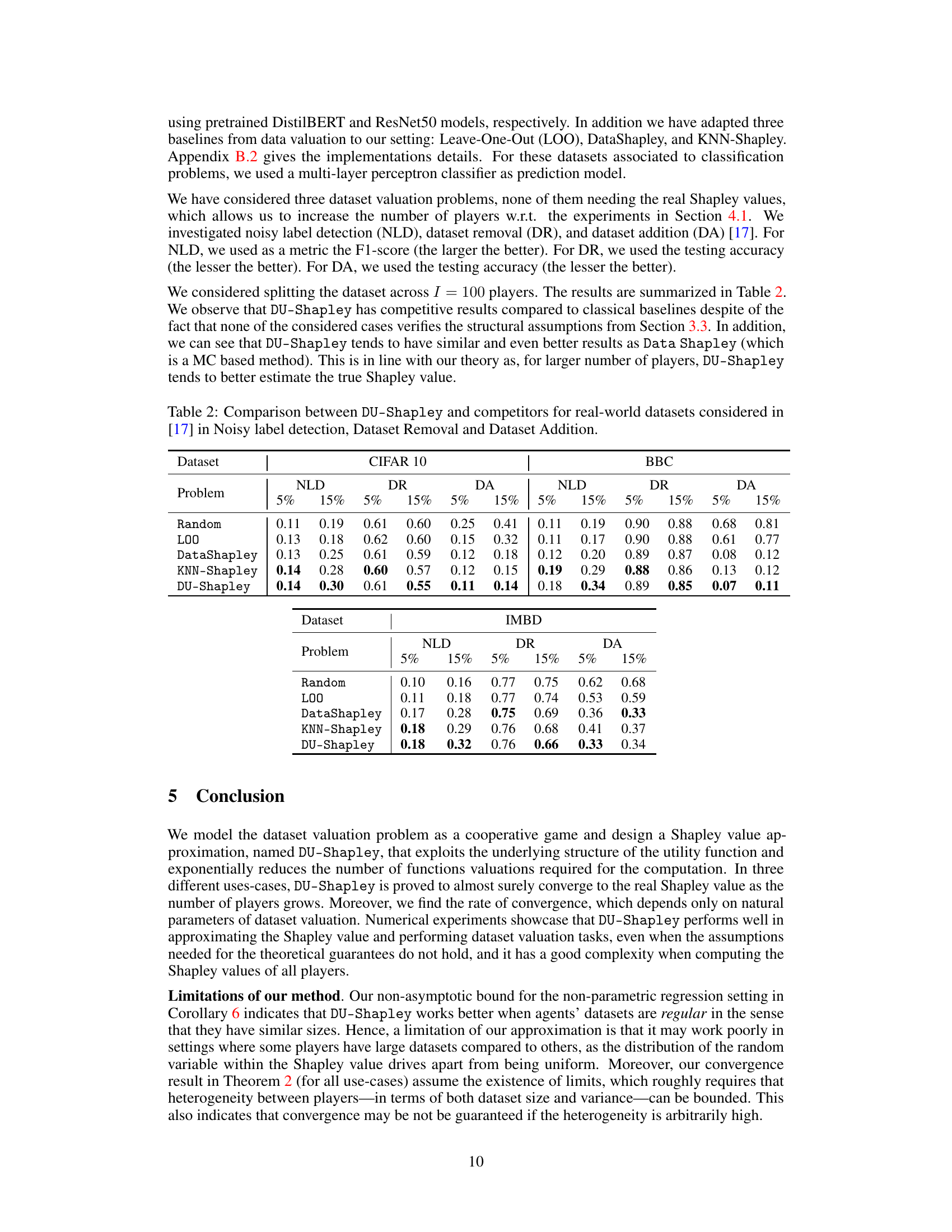
This table compares the performance of DU-Shapley against other methods (Random, LOO, DataShapley, and KNN-Shapley) for three dataset valuation problems: noisy label detection (NLD), dataset removal (DR), and dataset addition (DA). The results are shown for two datasets, CIFAR10 and BBC, and for different noise levels (5% and 15%). The metrics used are F1-score (for NLD), testing accuracy (for DR and DA), with lower values indicating better performance for DR and DA.
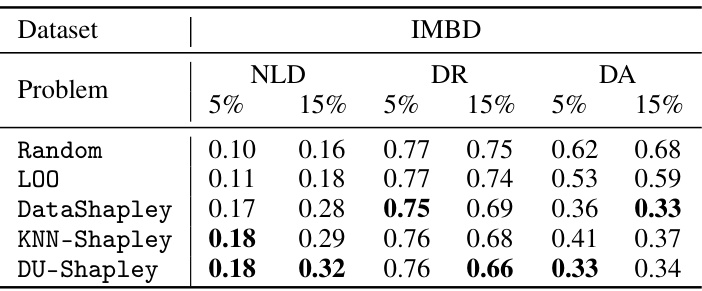
This table compares the performance of DU-Shapley against other methods (Random, LOO, DataShapley, KNN-Shapley) for three dataset valuation problems: noisy label detection (NLD), dataset removal (DR), and dataset addition (DA) on two real-world datasets (BBC and IMDB). The results show the performance metrics (F1-score for NLD, and testing accuracy for DR and DA) for different levels of noise (5% and 15%). It demonstrates how DU-Shapley compares to existing approaches on real-world data, showing competitive results, even when assumptions made for theoretical guarantees in the main paper are not completely satisfied.
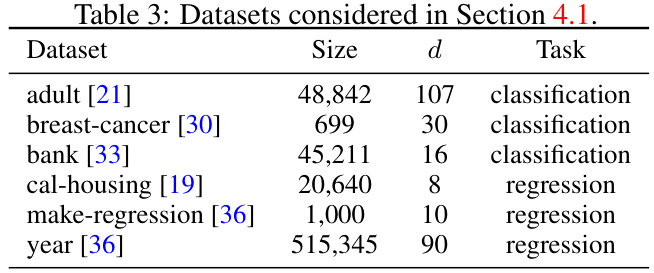
This table lists the six real-world datasets used in Section 4.1 of the paper for evaluating the performance of the proposed DU-Shapley method and comparing it with other methods. For each dataset, the table provides the dataset size, the number of features (d), and the type of machine learning task (classification or regression). These datasets represent a variety of problem types and sizes, allowing for a comprehensive evaluation of the algorithms.
Full paper#