↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Federated learning (FL) faces challenges with computationally intensive model training on resource-constrained devices, especially when data is highly heterogeneous across clients. Split Federated Learning (SFL) offers a solution by splitting the model and distributing training, aiming to improve efficiency while handling heterogeneity. However, there’s a lack of convergence analysis for SFL.
This paper fills that gap by providing a comprehensive convergence analysis of SFL. The analysis covers strongly convex, general convex, and non-convex objectives, accounting for heterogeneous data and scenarios where some clients might be unavailable. The researchers prove convergence rates and validate their theoretical findings with experiments, showing SFL’s superiority over FL and split learning in heterogeneous data settings.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in distributed machine learning, as it provides the first comprehensive convergence analysis of Split Federated Learning (SFL). This addresses a significant gap in the literature and offers valuable theoretical insights into SFL’s performance, particularly under heterogeneous data and partial client participation. The convergence rate analysis and extended analysis for non-convex objectives provide a strong theoretical foundation for future SFL algorithm development and optimization.
Visual Insights#

The figure illustrates the architecture of Split Federated Learning (SFL), comparing two main variants: SFL-V1 and SFL-V2. In both, a global model is split into client-side and server-side components. SFL-V1 has a separate server-side model for each client, updated in parallel. SFL-V2 uses a single server-side model updated sequentially. The figure showcases the parallel processing of client-side models and the interaction between clients and servers.

This table presents the theoretical upper bounds on the performance of the Split Federated Learning (SFL) algorithm under different scenarios and objective functions. It shows the convergence rate achieved by SFL-V1 and SFL-V2 under three different cases (strongly convex, general convex, and non-convex) for both full participation and partial participation of clients. The bounds are expressed in terms of the total number of rounds (T), smoothness parameter (S), strong convexity parameter (µ), variance of stochastic gradients (σ), and data heterogeneity (ε). The parameter Q represents the average participation rate of clients.
In-depth insights#
SFL Convergence#
The analysis of Split Federated Learning (SFL) convergence is a complex undertaking due to its hybrid nature, combining aspects of both Federated Learning (FL) and Split Learning (SL). Dual-paced updates, occurring at different frequencies for the client-side and server-side models, pose a significant challenge. The paper addresses this by providing a comprehensive convergence analysis for strongly convex, general convex, and non-convex objectives. A key contribution is the decomposition of the convergence analysis into server-side and client-side components, simplifying the analysis of this dual-paced system. Results show convergence rates of O(1/T) and O(1/√T) for strongly convex and general convex cases, respectively. The impact of data heterogeneity is explored, showing that convergence is slower with increased heterogeneity. Further, the analysis extends to practical scenarios of partial client participation, a common feature in real-world deployments, revealing additional challenges in convergence behavior. The theoretical results are validated by experiments, showing SFL outperforms FL and SL, particularly when dealing with high data heterogeneity and a large number of clients.
Heterogeneous Data#
The concept of “Heterogeneous Data” in federated learning is crucial because it acknowledges the reality that data isn’t uniformly distributed across participating clients. This non-IID (non-identically and independently distributed) nature of data significantly impacts model training because clients may have drastically different data distributions leading to model drift where the global model fails to generalize effectively. The challenge stems from the fact that averaging models trained on vastly different data may result in a suboptimal outcome. The paper likely investigates strategies to mitigate these negative impacts such as model splitting techniques or specialized aggregation algorithms to enhance the robustness and generalization capabilities of federated learning models. Addressing heterogeneous data is critical for enabling practical deployment of federated learning and the paper aims to offer solutions and insights on this front.
Dual-Paced Updates#
The concept of “Dual-Paced Updates” in federated learning, particularly within the context of split federated learning (SFL), highlights a key challenge and contribution of the research. It refers to the scenario where client updates and server updates happen at different speeds or frequencies. This dual-paced nature significantly complicates convergence analysis because it introduces an asymmetry in the learning process. Unlike traditional federated learning (FL), where the server and clients typically synchronize at the end of each round, SFL’s architecture allows for decoupled updates. The authors address this by developing novel decomposition techniques in their analysis, allowing them to separately study convergence of the client-side and server-side models. This is a crucial theoretical contribution, as it opens the way for understanding convergence behavior under conditions of data heterogeneity and partial client participation, both common in real-world deployments. The differing update paces in SFL may also offer advantages in terms of efficiency or resilience to client unavailability but require careful theoretical treatment to fully realize.
Partial Participation#
The concept of ‘partial participation’ in federated learning (FL) and its variants, such as split federated learning (SFL), addresses the realistic scenario where not all clients are available or active during every training round. This is particularly crucial for resource-constrained edge devices or mobile phones, often involved in FL, where connectivity and availability can be intermittent. This limitation necessitates modifications to the standard FL aggregation procedures, since a simple averaging of model updates from fully participating clients would introduce a bias towards those clients, affecting model accuracy. In SFL, where a global model is split across clients and servers, partial participation poses dual challenges: maintaining both client-side and server-side model integrity and ensuring convergence. Strategies for handling partial participation often involve weighting the contributions of participating clients based on their availability or other factors like data quantity, which demands careful analysis for convergence guarantees.
Future Directions#
Future research could explore tighter convergence bounds for split federated learning (SFL), potentially leveraging novel optimization techniques or refined analysis methods. Addressing the impact of data heterogeneity more comprehensively is crucial, investigating adaptive strategies or data pre-processing methods to improve SFL’s robustness. Furthermore, developing robust SFL algorithms for non-convex objectives is important, as many real-world machine learning tasks involve non-convex loss functions. Exploring different model splitting strategies and their impact on convergence and performance is warranted, optimizing the placement of the ‘cut layer’ based on data characteristics and model architecture. Finally, investigating federated learning’s resilience to client drift and partial participation is vital. This could involve advanced techniques such as client selection or weighting mechanisms to mitigate these issues, ultimately enhancing SFL’s applicability in practical distributed systems.
More visual insights#
More on figures

This figure shows the impact of the choice of cut layer on the performance of SFL-V1 and SFL-V2 algorithms. The x-axis represents the training round, and the y-axis represents the accuracy. There are four subfigures, each showing the results for a different combination of dataset (CIFAR-10 or CIFAR-100) and algorithm (SFL-V1 or SFL-V2). Within each subfigure, multiple lines represent different choices of cut layer (Lc), illustrating how the performance varies as the model split point changes. The results demonstrate how the choice of the cut layer influences the convergence speed and overall accuracy of the split federated learning.

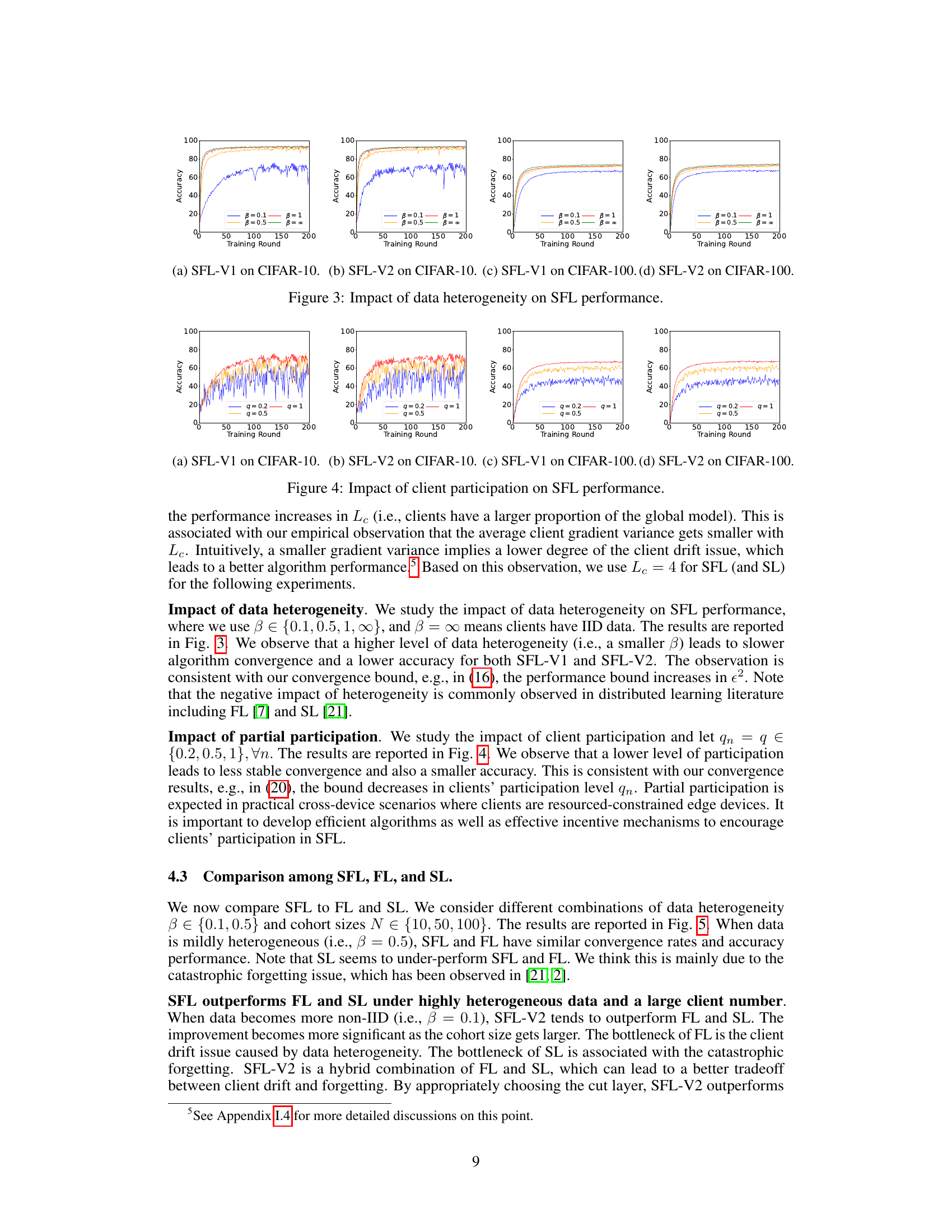
The figure shows the impact of data heterogeneity on the performance of two Split Federated Learning (SFL) algorithms (SFL-V1 and SFL-V2). Different values of beta (β) in a Dirichlet distribution, representing varying levels of data heterogeneity among clients, are used. Beta values of 0.1, 0.5, 1, and ∞ represent increasingly homogeneous data, with ∞ representing IID data. The graphs illustrate the accuracy achieved by each SFL algorithm over training rounds for CIFAR-10 and CIFAR-100 datasets. The results demonstrate that as data heterogeneity increases (smaller β), the accuracy of both SFL algorithms decreases, indicating a more challenging training scenario.

This figure shows the impact of client participation rate on the performance of SFL-V1 and SFL-V2 algorithms on CIFAR-10 and CIFAR-100 datasets. Different levels of participation (q = 0.2, 0.5, 1) are tested, showing how the availability of clients affects the algorithms’ convergence and accuracy.

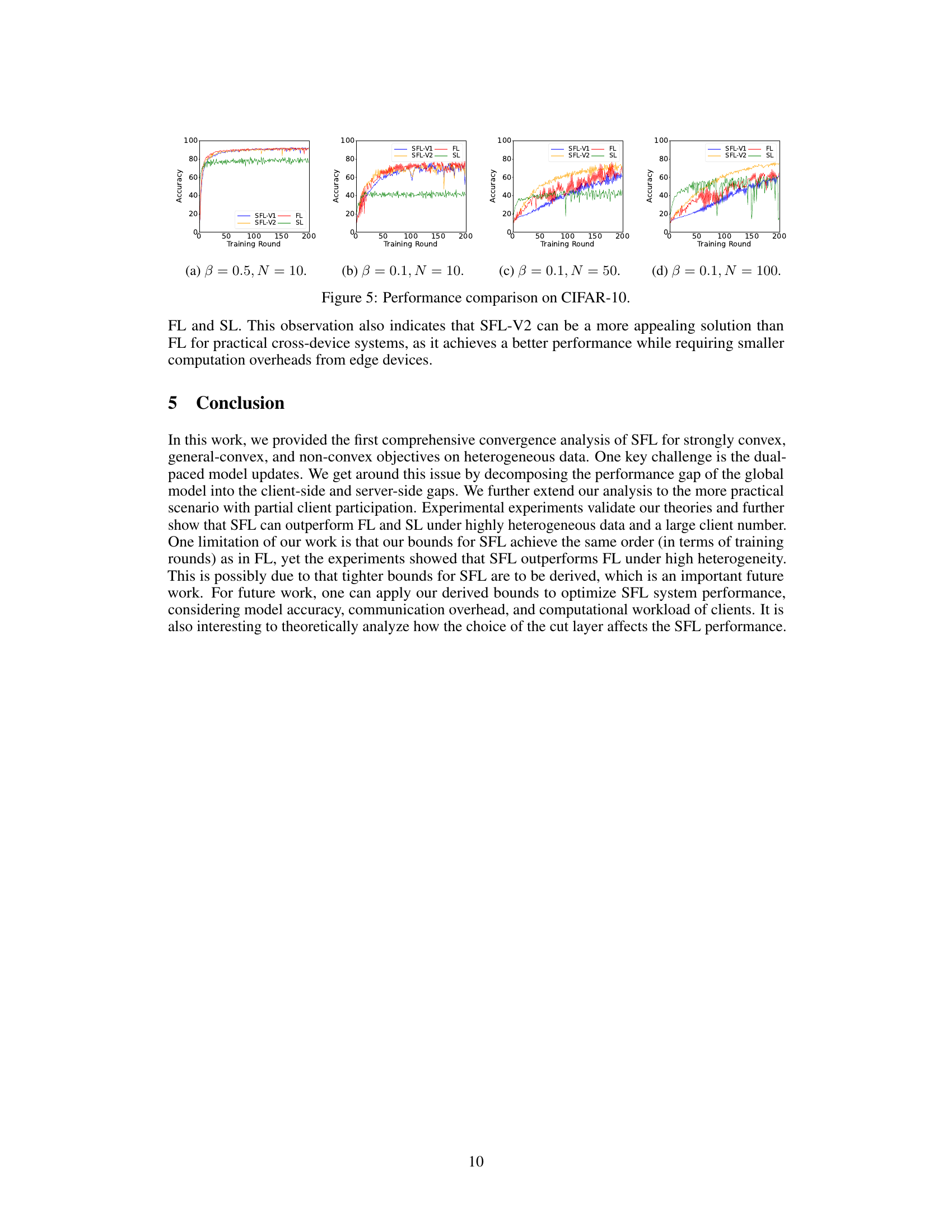
This figure compares the performance of SFL-V1, SFL-V2, FL, and SL under different combinations of data heterogeneity (β ∈ {0.1, 0.5}) and the number of clients (N ∈ {10, 50, 100}). The results show that when data is mildly heterogeneous (β = 0.5), SFL and FL have similar convergence rates and accuracy performance, with SL underperforming. However, under highly heterogeneous data (β = 0.1), SFL-V2 outperforms both FL and SL, especially as the number of clients increases. This highlights SFL-V2’s effectiveness in handling highly heterogeneous data with many clients.

This figure illustrates the architecture of the Split Federated Learning (SFL) framework. It shows two variants of SFL: SFL-V1 and SFL-V2. Both versions involve splitting the global model into client-side and server-side components. SFL-V1 has a separate server-side model for each client, while SFL-V2 uses a single server-side model. The figure highlights the parallel training at the client-side and the interaction between clients and servers (fed server and main server).

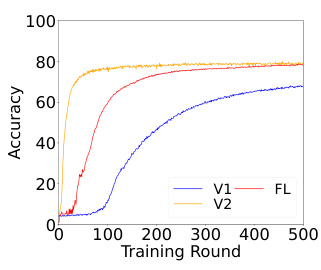
This figure compares the performance of SFL-V1, SFL-V2, FL, SL, FedProx, and FedOpt on CIFAR-10 dataset. Two subfigures are shown, one for β = 0.1 and N = 10 (a), and the other for β = 0.1 and N = 100 (b). Each line represents the accuracy over training rounds for a specific algorithm. The results show that SFL-V2 generally outperforms the other methods, especially when the number of clients (N) increases, indicating its effectiveness for heterogeneous data in large-scale federated learning.

The figure shows the impact of the number of local epochs (E) on the performance of split federated learning (SFL) algorithms (SFL-V1 and SFL-V2). The x-axis represents the training round, and the y-axis represents the accuracy. Four subfigures show results on CIFAR-10 (SFL-V1 and SFL-V2) and CIFAR-100 (SFL-V1 and SFL-V2), respectively. Each subfigure plots three curves, each corresponding to different values of E (E=2, E=5, and E=10). The results demonstrate that SFL generally converges faster with a larger E, highlighting the benefit of SFL in practical distributed systems.

The figure shows the impact of the choice of cut layer on the performance of split federated learning (SFL). The x-axis represents the training round, and the y-axis represents the accuracy. There are four lines in each subplot, each representing a different choice of cut layer (Lc = 1, 2, 3, 4). The subplots are arranged in a 2x2 grid, with each row representing a different dataset (CIFAR-10 and CIFAR-100) and each column representing a different SFL algorithm (SFL-V1 and SFL-V2). The results show that the performance of SFL generally increases as the cut layer moves towards the later layers, although the optimal cut layer may vary depending on the dataset and algorithm.
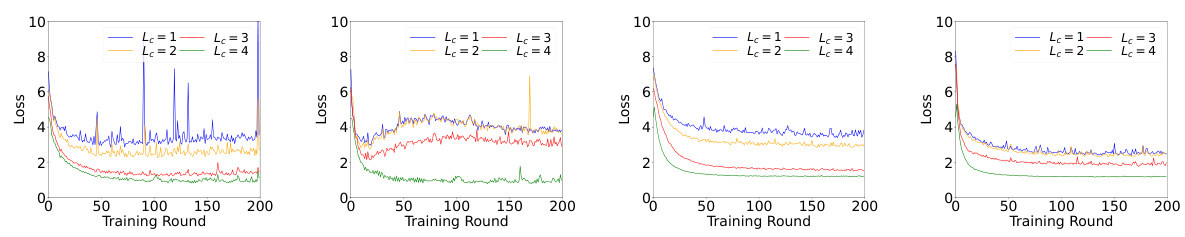
This figure shows the impact of the choice of cut layer (Lc) on the performance of Split Federated Learning (SFL). The x-axis represents the training rounds, and the y-axis represents the accuracy. Four different cut layers (Lc = 1, 2, 3, 4) are tested with both SFL-V1 and SFL-V2 algorithms on CIFAR-10 and CIFAR-100 datasets. The results demonstrate how the choice of the cut layer impacts the convergence and accuracy of SFL.

This figure visualizes the impact of the cut layer (Lc) on the performance of Split Federated Learning (SFL). The cut layer determines where the global model is divided into client-side and server-side models. The figure shows the training accuracy for both SFL-V1 and SFL-V2 algorithms on the CIFAR-10 and CIFAR-100 datasets across different cut layers (Lc = 1, 2, 3, 4). The results indicate how the choice of the cut layer influences the algorithm’s ability to converge and achieve high accuracy. It highlights the performance differences between SFL-V1 and SFL-V2 under varying data heterogeneity and model splitting strategies.

This figure visualizes the effect of varying client participation rates (q = {0.2, 0.5, 1}) on the performance of SFL-V1 and SFL-V2 across different datasets (CIFAR-10 and CIFAR-100). Each subfigure shows the training accuracy over 200 rounds. The results demonstrate that reducing client participation (lower q values) leads to slower convergence and lower overall accuracy for both SFL algorithms and across both datasets.

This figure visualizes the impact of different cut layer choices (Lc = {1, 2, 3, 4}) on the performance of the two SFL algorithms (SFL-V1 and SFL-V2). The x-axis represents the training round, and the y-axis represents the accuracy. Separate subplots are provided for each algorithm and for two datasets (CIFAR-10 and CIFAR-100). The results show how the choice of cut layer affects the convergence speed and final accuracy of the algorithms.
The figure compares the performance of SFL-V1, SFL-V2, FL, and SL on CIFAR-10 under different combinations of data heterogeneity (β ∈ {0.1, 0.5}) and cohort sizes (N ∈ {10, 50, 100}). It shows that when data is mildly heterogeneous (β = 0.5), SFL and FL perform similarly, while SL underperforms. However, under highly heterogeneous data (β = 0.1) and large client numbers, SFL-V2 outperforms FL and SL, highlighting its effectiveness in handling client drift and catastrophic forgetting issues.
More on tables

This table compares the upper bounds of the convergence rate for strongly convex objectives in different federated learning settings. The methods compared include Mini-Batch SGD, Federated Averaging (FL), Split Learning (SL), and Split Federated Learning (SFL). The table shows how the upper bounds vary based on factors such as the variance of stochastic gradients (σ²), smoothness (S), strong convexity (µ), the number of clients (N), the total number of rounds (T), and data heterogeneity (Ierr). Simplifications have been made to the SFL-V2 bound for easier comparison.

This table presents the upper bounds of convergence for different SFL methods (SFL-V1 and SFL-V2) under various scenarios (full participation and partial participation) and for different objective function types (strongly convex, general convex, and non-convex). The results demonstrate the convergence rates achieved by each method under the specified conditions, showing the impact of data heterogeneity and client participation levels on the performance of SFL.

This table compares the upper bounds of the convergence rate for strongly convex objectives in different federated learning algorithms: Mini-Batch SGD, FL, SL, and SFL. It highlights that the order of convergence for SFL and other algorithms is O(1/T).
Full paper#