↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Subgraph isomorphism-based graph retrieval is crucial but computationally expensive. Existing methods, like IsoNet, struggle with accuracy due to late interaction models and a lack of explicit alignment refinement. Early interaction methods, while intuitive, previously underperformed due to alignment issues and over-smoothing in graph neural networks (GNNs).
IsoNet++, a novel approach, tackles these issues by implementing an early interaction GNN that updates injective alignment iteratively. It introduces node-pair partner interaction, capturing richer relational information between graphs, and uses lazy alignment updates to reduce over-smoothing. Experiments show significantly improved retrieval accuracy over state-of-the-art methods, demonstrating the effectiveness of all three key innovations.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly improves the accuracy of subgraph matching for graph retrieval, a crucial task with broad applications. Its novel approach of iteratively refining alignment using early interaction GNNs offers a substantial improvement over existing methods. This work opens new avenues for research in graph neural networks and their applications to various domains.
Visual Insights#

This figure provides a comprehensive overview of the IsoNet++ architecture. Panel (a) illustrates the iterative refinement process of the model, involving multiple rounds of GNN propagation and alignment updates. Panels (b) and (c) detail the novel node-pair partner interaction mechanism employed in IsoNet++ (Node) and IsoNet++ (Edge), respectively, highlighting how node embeddings are influenced by partner nodes and edges.
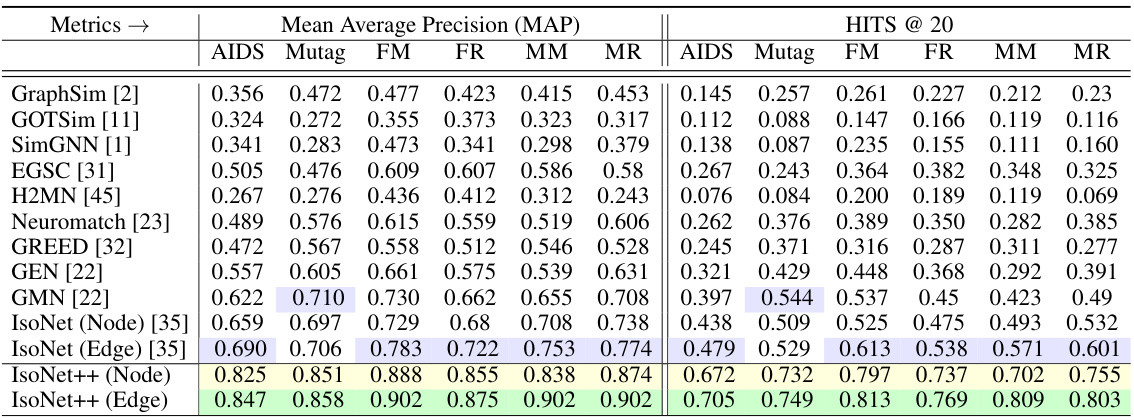
This table compares the performance of IsoNet++ (Node) and IsoNet++ (Edge) against 11 state-of-the-art graph retrieval methods across six datasets. The performance metrics used are mean average precision (MAP) and mean HITS@20. The table highlights the best and second-best performing methods.
In-depth insights#
Iterative Refinement#
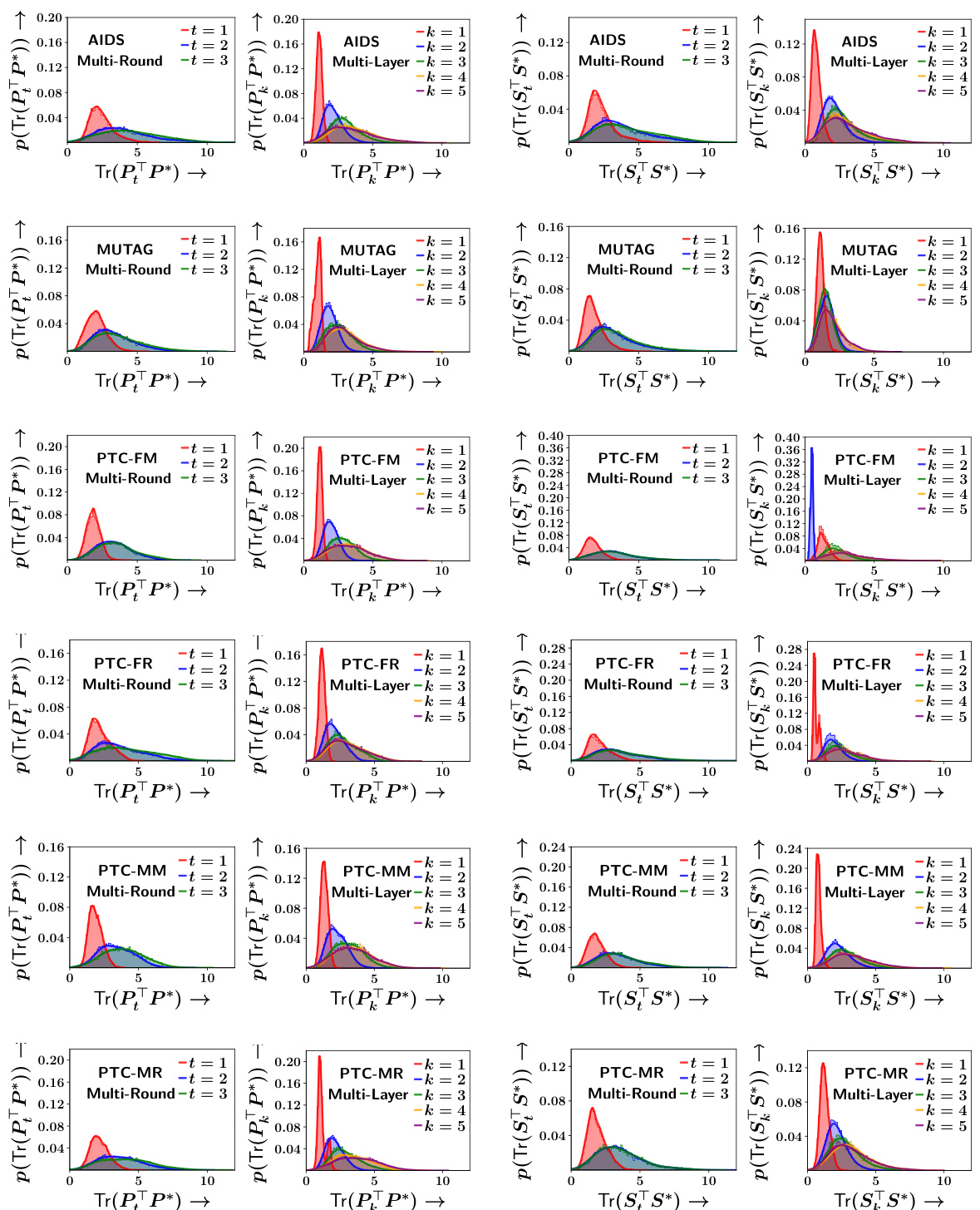
The concept of “Iterative Refinement” in the context of subgraph matching for graph retrieval suggests a powerful approach to enhance accuracy. The core idea is to iteratively improve an initial alignment between the nodes (or edges) of two graphs through successive rounds of refinement. Each round involves a graph neural network (GNN) that leverages the current alignment to compute node/edge embeddings, which are subsequently used to update the alignment for the next round. This contrasts with existing methods that compute alignments in a single step, often leading to less accurate results. This iterative process allows for progressively better alignments, as signals are refined through multiple interactions between the GNN and the alignment structure. The benefits of this approach are significant, especially as the refinements enable the GNN to consider increasingly sophisticated relationships between nodes, ultimately resulting in improved retrieval performance. Furthermore, it suggests an important trade-off between accuracy and computational cost that needs to be carefully considered. There might be diminishing returns on further refinements and the cost of additional rounds may not always justify the gains in accuracy. The choice of the number of iterations would depend heavily on available resources and desired performance.
Early Interaction GNN#
Early interaction in Graph Neural Networks (GNNs) for graph matching involves concurrently processing information from both input graphs at each layer, unlike late interaction which processes them separately initially. This concurrent processing is crucial for capturing intricate relationships and subtle similarities between graphs, particularly vital in subgraph isomorphism problems. The core idea is to leverage an alignment (mapping) between nodes or edges of the two graphs to guide message passing, effectively propagating information across graphs. The advantages include improved accuracy in capturing subtle relationships, leading to more refined alignments and better retrieval performance. However, designing an efficient and effective early interaction GNN requires careful consideration of computational complexity and potential oversmoothing issues of GNNs. Explicitly managing the alignment mechanism is vital, ensuring iterative refinement to enhance the quality of the matching, making early interaction techniques more practical and accurate for complex graph retrieval scenarios. Moreover, choices regarding the alignment update strategy (eager vs. lazy) and the extent of partner interaction (node-level vs. node-pair level) significantly influence performance.
Node-Pair Interaction#
The concept of ‘Node-Pair Interaction’ presents a novel approach to graph neural network (GNN) design, significantly enhancing subgraph matching accuracy. Instead of focusing on individual node interactions, this method considers pairs of nodes as fundamental units of interaction. By comparing node pairs across two graphs, it leverages the presence or absence of edges between nodes within each graph. This allows the model to capture richer relational information, particularly useful in identifying subgraph isomorphism. The existence of an edge in one graph but not the other provides a strong signal for refining the alignment between the graphs, leading to more accurate and refined subgraph matching. This approach surpasses traditional single-node attention mechanisms in its ability to extract crucial relational context, leading to improved retrieval performance.
Alignment Refinement#
The concept of ‘Alignment Refinement’ in the context of subgraph matching for graph retrieval is crucial for improving accuracy. It involves iteratively improving the mapping between nodes (or edges) of a query graph and a corpus graph. Initial alignments are often imperfect, so iterative refinement, using techniques like the Gromov-Wasserstein distance or other alignment metrics, is essential. This refinement is typically integrated with graph neural networks (GNNs), where the updated alignments guide the message passing and feature aggregation steps across the graphs. The iterative nature allows for the progressive refinement of the alignment, making the matching process more robust and less susceptible to noise or initial inaccuracies. Different refinement strategies (e.g., eager vs. lazy updates) exist and have different computational costs and accuracy trade-offs. This iterative procedure significantly impacts retrieval performance, as demonstrated by the enhanced accuracy achieved using this technique. The choice of refinement strategy (e.g., multi-round lazy updates), and the incorporation of novel elements such as node-pair interactions, are key design choices in creating an effective alignment refinement procedure. The success of the refinement heavily relies on the ability of the algorithm to learn meaningful representations, and to accurately capture the relational structure of both graphs.
Subgraph Matching#
Subgraph matching, a fundamental graph problem, seeks to identify whether a smaller graph (subgraph) exists within a larger graph. The challenge lies in efficiently finding isomorphic subgraphs, especially in massive datasets. The paper explores this challenge in the context of graph retrieval, where the goal is to locate graphs from a corpus containing a subgraph isomorphic to a query graph. The core idea is to leverage neural networks (GNNs) to learn meaningful representations of the graphs and utilize these representations for matching. The iterative refinement process, starting with an initial alignment and successively improving it through multiple rounds of GNN processing, is a key innovation to enhance accuracy. This iterative approach is particularly relevant to handle the complexities of subgraph isomorphism, as it progressively refines the alignment between nodes and edges in the query and corpus graphs, thereby increasing the likelihood of detecting the correct subgraph. The paper introduces node-pair partner interaction as a novel technique to improve the GNN’s ability to capture relevant relationships and refine the alignment more effectively. The algorithm’s efficiency is also considered, with an analysis of computational complexity presented to guide the selection of parameters. The overall methodology offers a promising direction in advancing subgraph matching algorithms for graph retrieval applications.
More visual insights#
More on figures
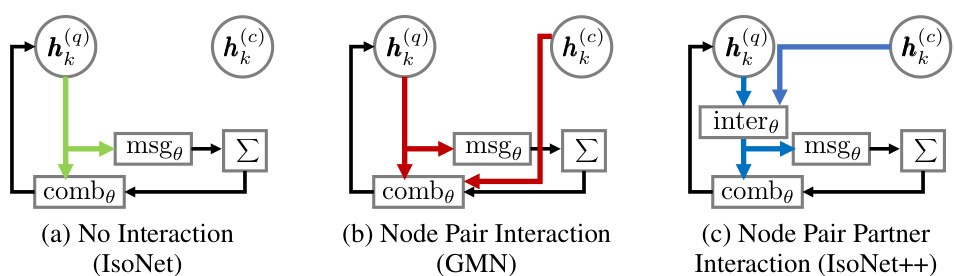
This figure illustrates the three different interaction modes between the query and corpus graphs in IsoNet, GMN, and IsoNet++. IsoNet uses no interaction, GMN uses node pair interaction, and IsoNet++ uses node pair partner interaction. The figure highlights the differences in how information is passed between graphs in each method, showing that IsoNet++ captures more information by considering node pairs instead of individual nodes.

This figure provides a high-level overview of the IsoNet++ model, illustrating its pipeline and the key innovations. Panel (a) shows the iterative refinement process, where multiple rounds of GNN propagation and alignment updates are performed. Panels (b) and (c) illustrate the novel node-pair partner interaction mechanism used in IsoNet++ (Node) and IsoNet++ (Edge) respectively, showcasing how node and edge embeddings are updated based on information from the aligned partners in the other graph.
This figure provides a high-level overview of the IsoNet++ model, illustrating its pipeline, node-pair partner interaction in both node and edge versions. Panel (a) shows the iterative refinement process of the alignment between two input graphs over multiple rounds, with each round involving multiple GNN layers. Panels (b) and (c) detail the novel node-pair partner interaction, contrasting how information from partner nodes/edges is incorporated in the node and edge versions of the model.
This figure provides a comprehensive overview of the IsoNet++ model, illustrating its pipeline, node-pair partner interaction, and edge-pair partner interaction. Panel (a) shows the iterative refinement process across multiple rounds, where each round involves K layers of GNN propagation and alignment updates. Panels (b) and (c) detail the novel node-pair and edge-pair partner interaction mechanisms, respectively, highlighting how these innovations capture richer information from the paired graph compared to traditional early interaction methods.
This figure provides a comprehensive overview of the IsoNet++ architecture. Panel (a) illustrates the iterative refinement process, where T rounds of K GNN layers are executed. Each round updates the alignment (P) based on node embeddings. Panels (b) and (c) detail the novel node-pair partner interaction for IsoNet++(Node) and IsoNet++(Edge) respectively, highlighting how node/edge embeddings are influenced by partners in the other graph, refining the alignment.
More on tables
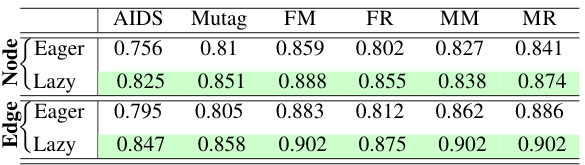
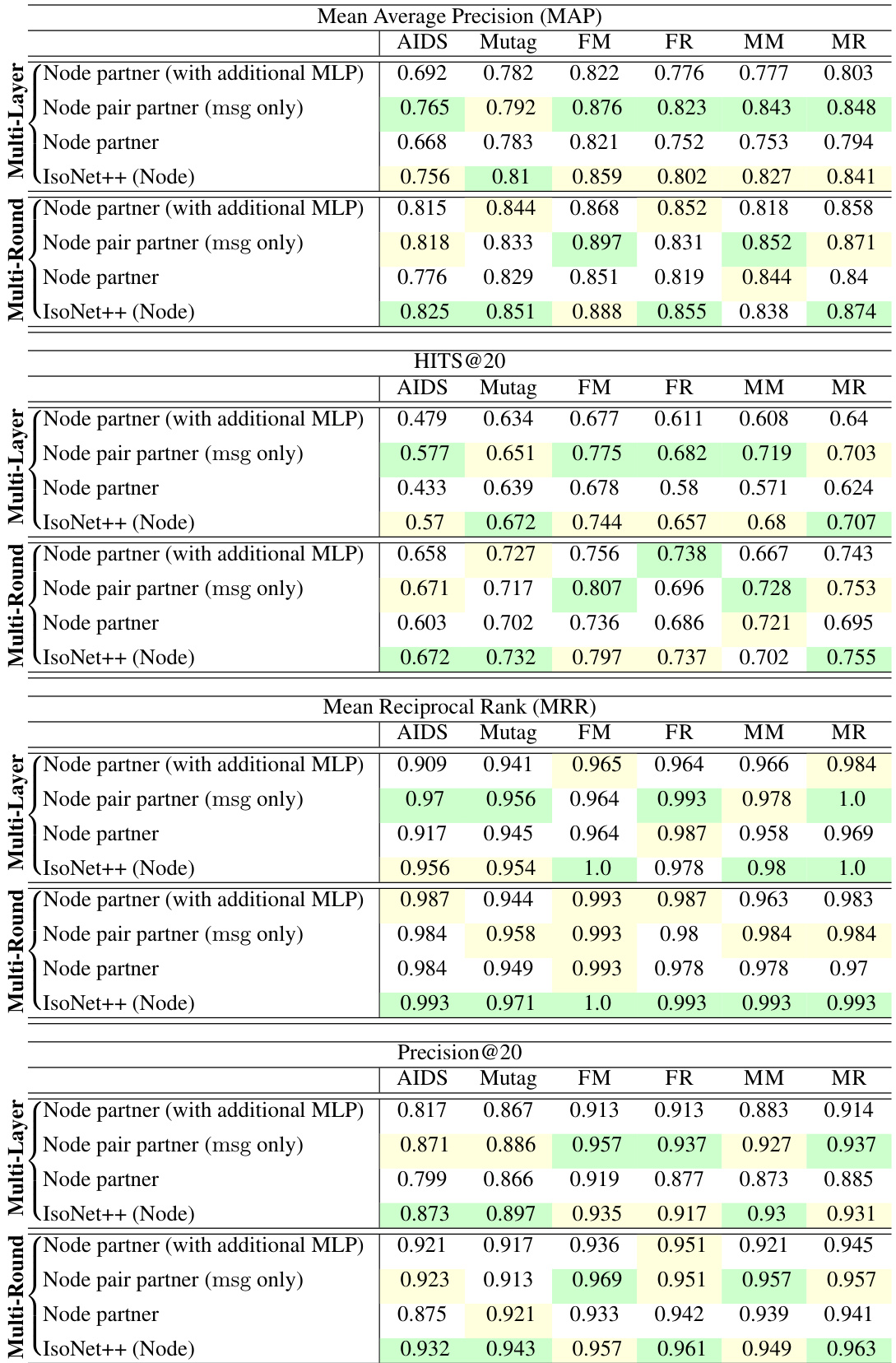
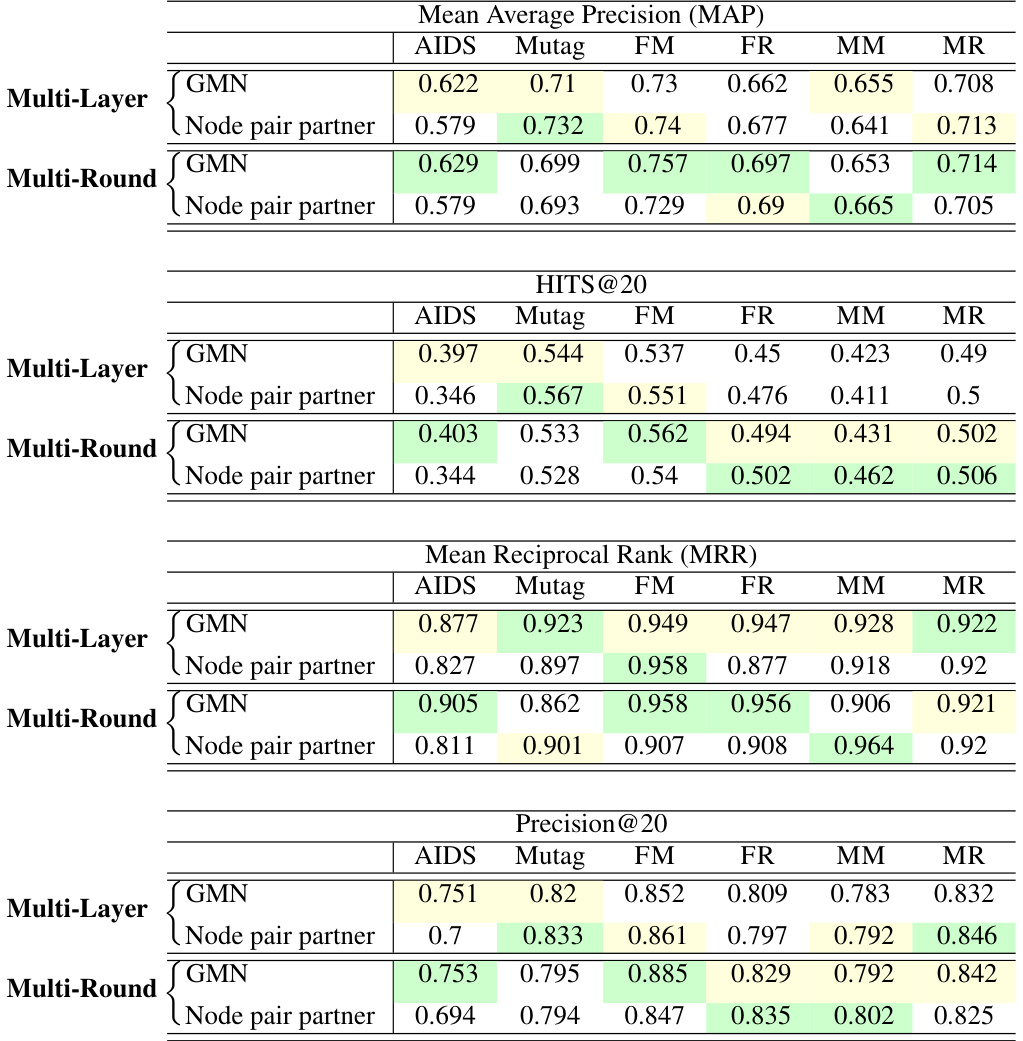
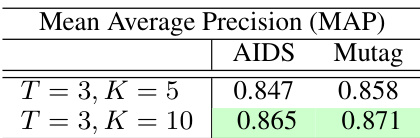
This table compares the performance of lazy multi-round and eager multi-layer versions of IsoNet++ for both node and edge alignment. MAP (Mean Average Precision) is used as the evaluation metric. The results show that the lazy multi-round approach generally outperforms the eager multi-layer approach, with the best-performing method highlighted in green.

This table compares the performance of different model variants. The first two rows show results for multi-round updates, comparing a model with only node partner interaction against the full IsoNet++ (Node) which incorporates node pair partner interaction. The last two rows show the same comparison but for multi-layer updates. The highest MAP values for each dataset are highlighted in green.

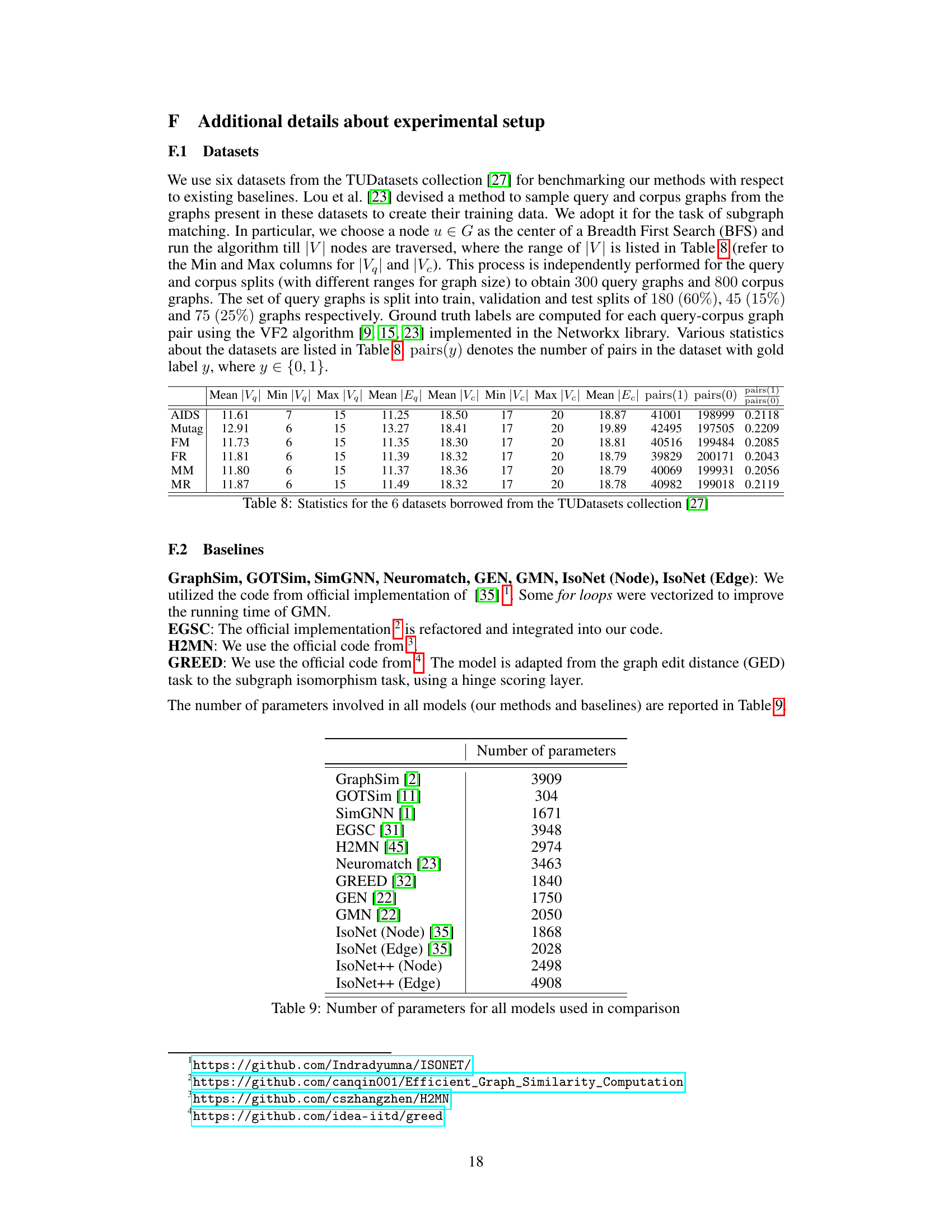
This table presents key statistics for six datasets used in the paper’s experiments, all sourced from the TUDatasets collection [27]. The statistics provided for each dataset (AIDS, Mutag, PTC-FM, PTC-FR, PTC-MM, PTC-MR) include the average and range of the number of nodes in the query graphs (|Vq|), the average number of edges in the query graphs (|Eq|), the average and range of the number of nodes in the corpus graphs (|Vc|), the average number of edges in the corpus graphs (|Ec|), and the proportion of relevant graph pairs (pairs(1) / (pairs(1) + pairs(0))). These statistics provide context for understanding the characteristics of the data used for evaluating the proposed subgraph matching methods.

This table lists the number of parameters for all the models used in the paper’s experiments, including both the proposed IsoNet++ models and several state-of-the-art baseline models for comparison. The number of parameters is an indicator of model complexity.

This table shows the best random seed used for each model during training. The best seed was selected based on the Mean Average Precision (MAP) score achieved on the validation set after convergence (for IsoNet (Edge), GMN, and IsoNet++ (Node)) or after 10 training epochs (for all other models). The selection of the best seed helps ensure reproducibility and consistency in the experimental results.
This table presents the best margin hyperparameter values for each of the baseline models used in the paper’s experiments, across six different datasets (AIDS, Mutag, FM, FR, MM, MR). The margin hyperparameter is used in the asymmetric hinge loss function, a ranking loss used to train the models. For each dataset and model, the table shows the margin value that resulted in the best performance during training.

This table compares the performance of IsoNet++ (Node) and IsoNet++ (Edge) against eleven other state-of-the-art graph retrieval methods across six datasets. The performance metrics used are Mean Average Precision (MAP) and mean HITS@20. The table highlights the best and second-best performing methods for each dataset.

This table compares the performance of IsoNet++ (Node) and IsoNet++ (Edge) against eleven state-of-the-art methods for graph retrieval on six real-world datasets. The performance metrics used are Mean Average Precision (MAP) and mean HITS@20. The table highlights the best and second-best performing methods.

This table compares the performance of IsoNet++ (Node) and IsoNet++ (Edge) against eleven other state-of-the-art graph retrieval methods across six datasets. Performance is evaluated using Mean Average Precision (MAP) and HITS@20. The table highlights the best and second-best performing models. It notes that the MAP values for IsoNet++ (Edge) on three datasets are very close but not exactly identical.
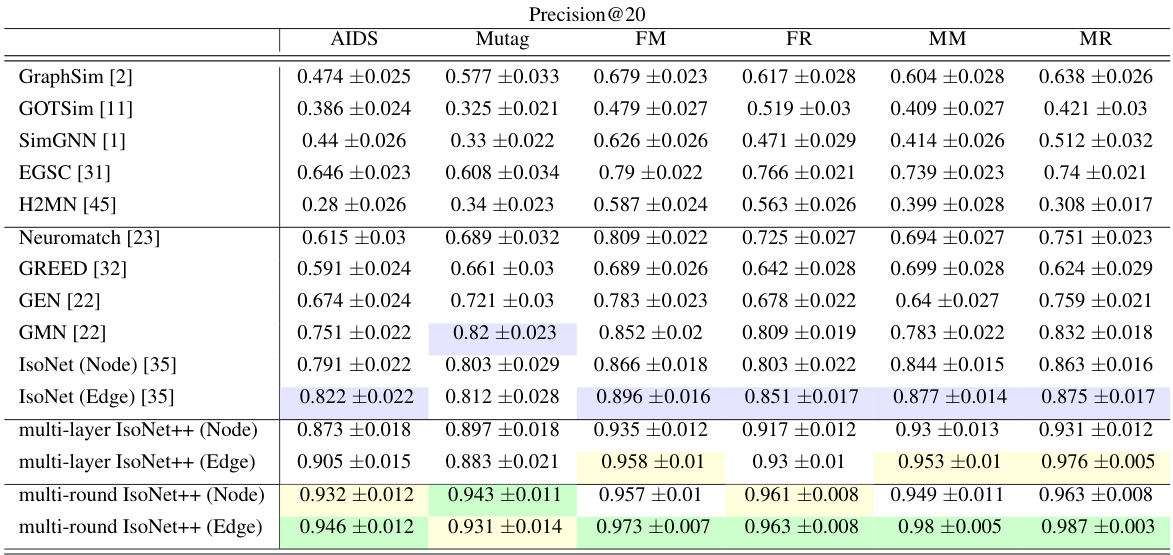
This table compares the performance of IsoNet++ (Node) and IsoNet++ (Edge) against eleven state-of-the-art graph retrieval methods across six datasets. Performance is evaluated using Mean Average Precision (MAP) and HITS@20. The table highlights the best and second-best performing methods.

This table compares the performance of IsoNet++ (Node) and IsoNet++ (Edge) against eleven state-of-the-art methods for graph retrieval on six real-world datasets. Performance is evaluated using Mean Average Precision (MAP) and mean HITS@20. The table highlights the best and second-best performing methods.
This table compares the performance of IsoNet++ (Node) and IsoNet++ (Edge) against eleven state-of-the-art graph retrieval methods across six datasets. The performance metrics used are Mean Average Precision (MAP) and mean HITS@20. The table highlights the best and second-best performing methods.
This table compares the performance of IsoNet++ (Node) and IsoNet++ (Edge) against eleven other state-of-the-art graph retrieval methods across six datasets. The performance metrics used are Mean Average Precision (MAP) and mean HITS@20. The table highlights the best and second-best performing methods for each dataset.
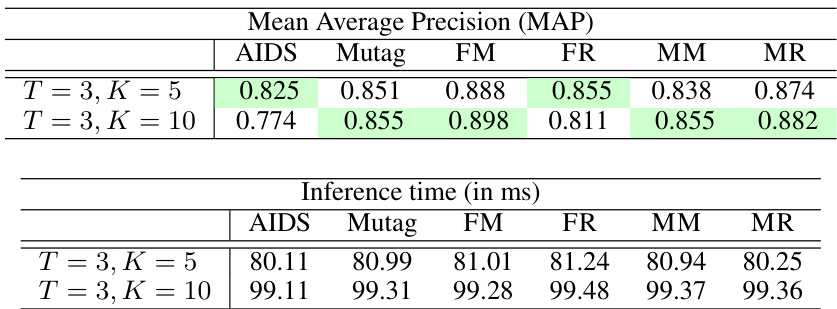
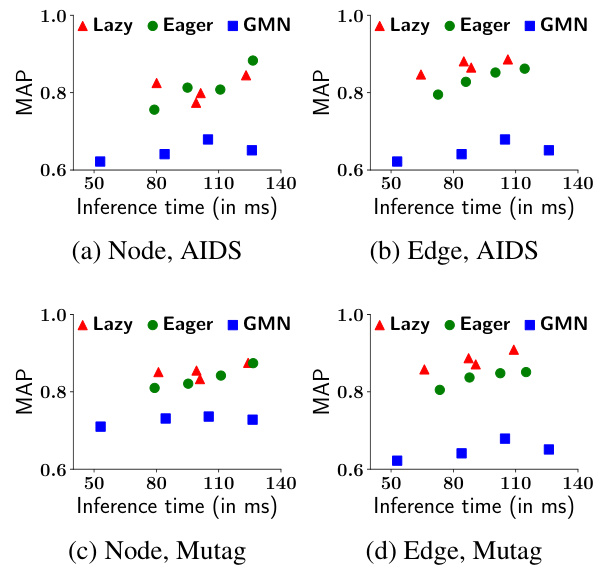
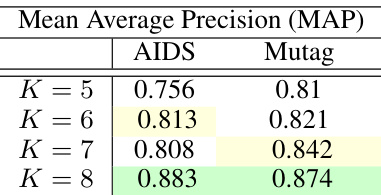
This table presents a comparison of the mean average precision (MAP) and inference time for different values of K (number of GNN layers) in the multi-round lazy IsoNet++ (Node) model, while keeping T (number of rounds) fixed at 3. The results show how the model’s performance and computational cost change as the number of layers increases. The best performing K in terms of MAP is highlighted.
This table shows a comparison of the Mean Average Precision (MAP) and inference time (in milliseconds) for different values of K (number of GNN layers) in each round of the multi-round lazy IsoNet++ (Node) model. The number of rounds, T, is kept constant at 3. The table demonstrates the trade-off between accuracy and computational cost as K increases.
This table shows the results of experiments evaluating the trade-off between accuracy (measured by Mean Average Precision, or MAP) and inference time for different values of K in the multi-layer eager variant of IsoNet++ (Node). The best performing K value is highlighted in green, indicating the optimal balance between accuracy and inference speed.

This table shows the performance (MAP) and inference time of the multi-layer eager variant of IsoNet++ (Edge) with varying number of layers (K). The best performing K value is highlighted in green, and the second best is highlighted in yellow. The inference time increases linearly with K.
This table shows the results of experiments comparing different numbers of propagation layers (K) in the IsoNet++ (Edge) model while keeping the number of rounds (T) fixed at 3. It shows the Mean Average Precision (MAP) achieved and the inference time. The best and second-best performing values of K for each dataset, as judged by MAP score, are highlighted.

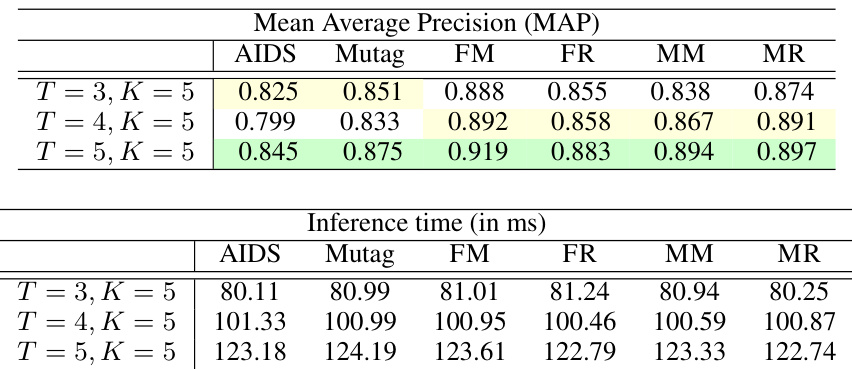
This table shows the relationship between the mean average precision (MAP) and inference time for the multi-round lazy version of the IsoNet++ (Edge) model. The number of rounds (T) is held constant at 3, while the number of GNN layers in each round (K) is varied. The table highlights how the MAP score and inference time change as K increases. This analysis helps in understanding the trade-off between model accuracy and computational cost.

This table shows the results of experiments on multi-round lazy IsoNet++ (Edge) model with a fixed number of GNN layers (K=5) and varying number of rounds (T=3,4,5). The Mean Average Precision (MAP) and inference time (in milliseconds) are reported for AIDS and Mutag datasets. The best performing T value in terms of MAP is highlighted in green, and the second best in yellow. The table demonstrates the trade-off between accuracy and inference time as the number of rounds increases.

This table shows how the mean average precision (MAP) and inference time vary for the multi-round lazy version of IsoNet++ (Edge) when the number of rounds (T) is changed while keeping the number of layers (K) constant. The best and second-best values of T according to the MAP score are highlighted in green and yellow, respectively.

This table shows the results of experiments evaluating the trade-off between accuracy (measured by Mean Average Precision, MAP) and inference time for the multi-layer eager variant of the IsoNet++ (Edge) model. Different values of K (number of propagation steps in the GNN) were used, and the MAP and inference time are reported for each. The best and second-best performing values of K, based on MAP, are highlighted.

This table presents the results of experiments evaluating the impact of varying the number of propagation layers (K) in the GMN model on its mean average precision (MAP) and inference time. The experiment involved varying K while keeping other parameters constant and measuring MAP and inference time across six datasets (AIDS, Mutag, FM, FR, MM, MR). The best and second-best performing values of K according to MAP scores are highlighted.

This table shows the result of experiments on the effect of varying the number of propagation layers (K) on the performance of the GMN model. It presents the Mean Average Precision (MAP) and inference time for different values of K (5, 8, 10, and 12). The best and second-best performing values of K, based on MAP scores, are highlighted in green and yellow, respectively.

This table shows the results of experiments evaluating the effect of varying the number of propagation layers (K) in IsoNet (Edge) on the mean average precision (MAP) and inference time. The results indicate that increasing K beyond a certain point does not lead to improved MAP scores, suggesting a potential trade-off between model complexity and performance.

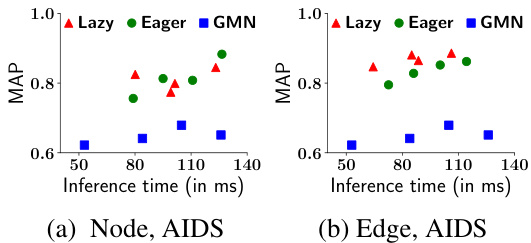
This table shows a breakdown of the inference time for different model variations. It separates the time spent on embedding computation from the time spent on updating the alignment matrices. The results highlight that for multi-layer models, matrix updates are the most time-consuming part, while in multi-round models, embedding computation and matrix updates have a more even contribution to the total inference time. This difference stems from how frequently the alignment matrices are updated (at every layer vs. at the end of each round).

This table compares the performance of IsoNet++ (Node) and IsoNet++ (Edge) against eleven state-of-the-art methods for graph retrieval on six datasets. The performance metrics used are Mean Average Precision (MAP) and mean HITS@20. The table highlights the best and second-best performing methods.
Full paper#