Sample-Efficient Agnostic Boosting

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it significantly improves the sample efficiency of agnostic boosting, a long-standing challenge in machine learning. This advancement is particularly relevant as it addresses the limitations of existing methods that are significantly less efficient than the ideal approach (ERM). The improved algorithm not only enhances theoretical understanding but also paves the way for practical applications of agnostic boosting in various fields, such as reinforcement learning.

Visual Insights

#

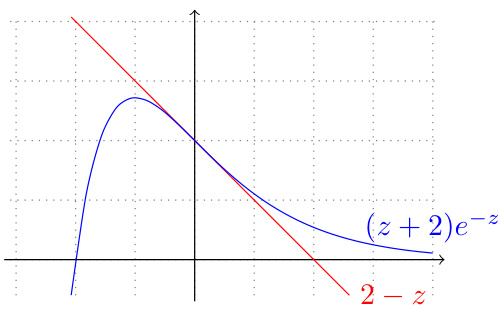
This figure shows the piecewise potential function φ(z), which is defined as the pointwise maximum of the two functions (z+2)e⁻ᶻ and 2-z. The blue curve represents (z+2)e⁻ᶻ and the red line represents 2-z. The graph visually demonstrates how the piecewise function combines the two functions to define a continuously differentiable potential function used in the agnostic boosting algorithm.

This table compares the sample and oracle complexities of different agnostic boosting algorithms, including the proposed algorithm, to achieve an error within epsilon of the optimal classifier. It shows that the new algorithm significantly improves sample complexity without increasing computational complexity.

In-depth insights

#

Agnostic Boosting

#

Agnostic boosting is a machine learning technique focusing on improving the accuracy of weak learners without making strong assumptions about the data’s underlying distribution. Unlike traditional boosting methods that assume the existence of a perfect classifier (realizable case), agnostic boosting handles scenarios where no such classifier exists (agnostic case). The core challenge lies in efficiently aggregating weak learners that only marginally outperform random guessing to create a strong learner with high accuracy. Sample efficiency is a critical concern as agnostic boosting typically requires many samples, significantly more than other methods. The goal is to minimize sample complexity and ensure the resulting model generalizes well to unseen data. Recent research has focused on improving the sample efficiency of agnostic boosting through innovative algorithms and theoretical analyses. Key improvements include leveraging sample reuse and the development of novel analysis techniques that circumvent reliance on uniform convergence arguments.

Sample Reuse

#

The concept of ‘sample reuse’ in machine learning is a powerful technique that aims to maximize the information extracted from limited datasets. It fundamentally alters the traditional approach of drawing fresh samples for each iteration of a learning algorithm. Instead, it leverages previously used samples, carefully reintroducing them to enhance learning efficiency and improve generalization performance. This technique is particularly beneficial in scenarios with scarce data, a common challenge in many real-world applications. The key to successful sample reuse lies in the careful design of sampling strategies and relabeling schemes to avoid introducing bias or compromising the integrity of the learned model. Effective sample reuse algorithms often incorporate advanced techniques to estimate and manage potential biases, ensuring robustness and reliable results. A major advantage of this approach is the reduction in required samples for achieving a desired level of accuracy. This directly translates to cost savings in data acquisition and computational resources, making sample reuse a valuable tool in resource-constrained learning environments. The effectiveness of sample reuse is heavily dependent on the nature of the learning problem and the algorithm itself, requiring careful consideration and potentially innovative techniques to ensure its proper application. Future research should focus on developing more sophisticated sample reuse techniques applicable across a broader range of learning tasks.

Oracle Complexity

#

Oracle complexity, in the context of machine learning algorithms, specifically boosting algorithms, refers to the number of calls made to a weak learner during the learning process. It’s a crucial measure of computational efficiency, separate from sample complexity (the number of training examples). A lower oracle complexity is desirable because it indicates that the algorithm requires fewer calls to the weak learner to achieve a given level of accuracy. This is important as each call to a weak learner might be computationally expensive. The paper focuses on reducing the sample complexity of agnostic boosting algorithms while maintaining reasonable oracle complexity. The improved sample efficiency is achieved through a careful sample reuse strategy, unlike previous methods that used fresh samples for every boosting round. While the new algorithm initially exhibits a higher oracle complexity, a second result demonstrates that modifications can reduce it to levels comparable to existing algorithms. This demonstrates a trade-off between sample and oracle complexities, allowing practitioners to prioritize sample efficiency if computation is less of a concern. The analysis highlights the importance of carefully balancing these two complexities, as neither one should be optimized at the significant expense of the other.

Infinite Classes

#

The extension to infinite hypothesis classes presents a significant challenge in agnostic boosting. Traditional techniques relying on symmetrization and Rademacher complexity are inapplicable due to the intricate dependencies introduced by sample reuse across boosting rounds. The authors address this by employing L1 covering numbers, a more suitable measure for analyzing data with dependencies. This approach allows them to bound the generalization error, ultimately establishing a sample complexity that scales favorably even for infinite hypothesis spaces. The theoretical justification for this extension is non-trivial, demanding innovative empirical process theory to bridge the gap between finite and infinite settings. The success of this approach underscores the algorithm’s robustness and its potential for handling diverse, expressive hypothesis classes, moving beyond the limitations of previous boosting methods restricted to finite spaces.

Future Work

#

The research paper’s ‘Future Work’ section presents exciting avenues for further exploration. Improving the oracle complexity of the proposed agnostic boosting algorithm is a primary goal, aiming to match or surpass the efficiency of existing methods. This would involve refining the algorithm’s design or developing novel analysis techniques. Another crucial area is closing the sample complexity gap between the proposed algorithm and Empirical Risk Minimization (ERM). Achieving comparable sample efficiency to ERM, without compromising computational efficiency, would significantly enhance the practical applicability of the boosting technique. Furthermore, extending the applicability of the algorithm to broader classes of problems and exploring more sophisticated weak learners would be valuable. This involves adapting the algorithm to handle diverse data types and addressing scenarios with non-standard noise models, such as heavy-tailed noise. Finally, a thorough experimental validation of the theoretical findings is vital to demonstrate the practical benefits and limitations of the algorithm. This necessitates evaluating its performance on large datasets and comparing it with state-of-the-art techniques across a range of real-world machine learning problems.

More visual insights

#

More on tables

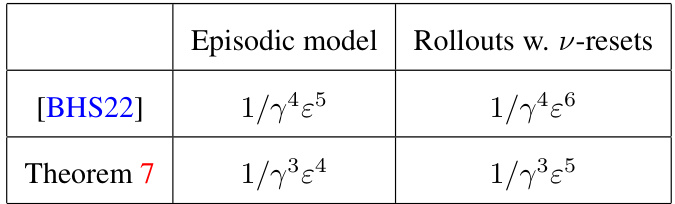
This table compares the sample complexities of two different reinforcement learning approaches (episodic model and rollouts with v-resets) using a γ-weak learner. The sample complexity is expressed in terms of ε (excess error) and γ (weak learner’s edge). The table shows that using the proposed algorithm (Theorem 7) significantly reduces the sample complexity compared to a previous approach ([BHS22]).

This table compares the sample and oracle complexities of several agnostic boosting algorithms, including the proposed one, with the computationally expensive Empirical Risk Minimization (ERM) method. It highlights the trade-off between sample efficiency and computational cost, showing that the new algorithm significantly improves sample efficiency while maintaining reasonable computational complexity.

Full paper

#